智能反射表面辅助的无线携能通信网络资源分配算法

孙巍，宋清洋，郭磊

（1.东北大学计算机科学与工程学院，辽宁 沈阳 110089；2.重庆邮电大学智能通信与网络安全研究院，重庆 400065）

0 引言

随着物联网中无线能量受限设备数量的大幅增加，未来网络需要兼顾高传输速率和持续能源供应两方面问题。近年来，无线携能通信（SWIPT,simultaneous wireless information and power transfer）[1-4]被认为是一种解决无线通信设备能量受限问题的有效技术。该技术利用射频信号可以同时携带数据信息和电磁能量的双重性，在对设备进行数据传输的同时进行无线充电，从而有效解决物联网中设备能量受限的问题，减少设备对电池的依赖，并提供足够的能量来支持更高性能的通信。

然而，在无线携能通信网络中，由于无线信道的随机性和严重的信道衰落，会导致接收端接收的能量和信息较弱。近年来，得益于射频微机电系统的快速发展，一种可重构智能表面，又名智能反射表面（IRS,intelligent reflecting surface）的技术受到广泛的关注[5]。该技术可以在一定程度上根据通信需求重构无线传播环境，是未来6G 通信领域潜在的关键技术之一[6]。智能反射表面由大规模低成本、小尺寸的被动散射元件阵列构成，如金属或介电粒子[7]，通过软件定义的方式对每个散射元件进行实时控制，从而改变散射元件上的物理参数，实现对入射射频信号的反射电磁特性（即相位、振幅、频率等）控制，进而提升整个网络系统的性能。由于智能反射表面技术可以有效地改善系统的频谱效率和能量效率，目前已经在各类无线通信系统中应用，如多输入单输出系统[8]、毫米波系统[9]、边缘计算系统[10]、非正交多址系统[11]等。

为了在解决能量受限设备的短生存时间的同时提升系统的通信性能，众多学者将智能反射表面引入无线携能通信网络中，在智能反射表面辅助的无线携能网络中，适当调整智能反射表面处反射波束的形成，将反射信号与来自其他路径的信号进行叠加，以增强设备处的接收信号功率，有效地提高无线能量传输效率。目前，一些学者针对采用独立接收机架构（同时存在能量收集（EH,energy harvesting）接收机和信息接收机）的智能反射表面辅助的无线携能通信网络开展了深入研究[12-17]。文献[12]通过采用基于罚函数法和块坐标下降法对主动波束成形和被动波束成形进行联合设计，来最小化发射功率。文献[13]针对智能反射表面辅助的多输入多输出无线携能通信网络，研究加权速率和最大化问题。文献[14]研究了最大所有能量收集接收器的收获功率加权和。文献[15]通过联合优化基站的信息和能量传输波束成形以及智能反射表面被动波束成形，来最大化所有能量接收器的最小接收功率。文献[16]通过利用基于半正定松弛（SDR,semidefinite relaxation）的交替迭代算法优化波束成形矢量和智能反射表面上的相移，来最大化系统的安全能量效率。文献[17]设计了一种基于连续凸近似（SCA,successive convex approximation）和SDR的联合优化策略，从而使系统速率和最大化。然而，在大多数情况下，特别是在物联网应用中，网络设备需要在保证其进行解码数据的同时进行能量收集来延长自身的生存周期。具备这种能力的设备通常配备共址接收机架构，并且在实际中应用广泛。文献[18]研究了设备处采用功率分割接收器的智能反射表面辅助的无线携能通信网络，通过优化相移来最大化实际数据速率，并与传统的解码转发中继系统进行性能比较。然而，文献[18]考虑的是用户和基站之间不存在直连链路的情况，且仅关注由单天线基站和单个用户组成的无线携能通信网络。文献[19]考虑联合基站发射波束成形、智能反射表面处相移及用户侧功率分割比来最小化基站处的发射功率。为了进一步提升网络性能，文献[20]研究了智能反射表面辅助的非正交多址携能通信网络的基站发射功率最小化问题。文献[19-20]均采用了常见的基于SDR的交替迭代算法来获取问题的次优解。但在优化变量的维数或者用户数量很大的情况下，这种半正定松弛技术通常无法产生满足秩一约束的解从而导致性能下降。

目前的研究缺乏对由配有功率分割架构的终端设备构成的智能反射表面辅助无线携能通信网络最佳速率和性能的研究。为了实现在延长网络生存周期的同时提高网络总吞吐量，本文将对所考虑的系统进行深入研究，并提出一种以速率和最大化为目标的资源分配方案。具体地，本文主要的研究工作如下。

1) 建立下行智能反射表面辅助的无线携能通信网络资源分配模型。通过联合优化发射波束成形、功率分割比和智能反射表面处的相移来最大化整个网络的速率和，并满足最小能量收集约束、发射功率约束、功率分割比约束及相移约束。所构建的速率和最大化资源分配问题是一个非凸、非线性、多变量耦合的优化问题，难以直接求解。

2) 针对上述的非凸二次规划问题，设计了一种有效的基于块坐标下降的迭代算法。具体来说，首先，利用块坐标下降法将原始问题划分成3 个子问题。然后，针对发射波束成形设计和功率分割比决策2 个子问题，利用连续凸近似方法进行求解。针对智能反射表面相移设计子问题，采用黎曼流形方法进行求解。最后，对本文所提算法的计算复杂度进行分析。

3) 仿真结果验证了所提算法的收敛性性能，并表明在无线携能通信系统中使用智能反射表面可以有效地提升系统的速率和。与现有方案相比，本文所提方案在提高速率和方面具有很大优势。

1 系统模型

本文考虑一个由配置M根天线的基站和K个单天线物联网设备构成的下行多输入单输出无线携能通信网络，下行智能反射表面辅助的无线携能通信网络如图1 所示。基站采用无线携能通信技术向所有设备同时提供信息和能量。为了进一步提升通信系统的性能，本文采用一个具有N个反射单元的智能反射表面来协助基站与物联网设备之间的通信。智能反射表面配有智能控制器，可以调控每个反射单元上的相移和幅度。由于高路径损耗，被智能反射表面反射两次或两次以上的信号可以忽略不计。假设基站、智能反射表面和物联网设备之间的所有信道均采用块衰落模型，即在每一个时间块内信道系数变化缓慢。同时，本文假设基站采用现有的信道估计方法，如基于并行因子分解的信道估计框架[21]，基于压缩感知的方法[22]等，可以获得所有信道较为准确的信道信息，该假设与多数智能反射表面辅助系统研究中的假设相同[23-25]。此外，本文考虑的具有理想信道状态信息的场景可以作为实际场景的性能上限。本文假设基站处进行线性传输预编码，其中每个物联网设备被分配一个专用的信息波束。因此，基站发送的信号可以表示为

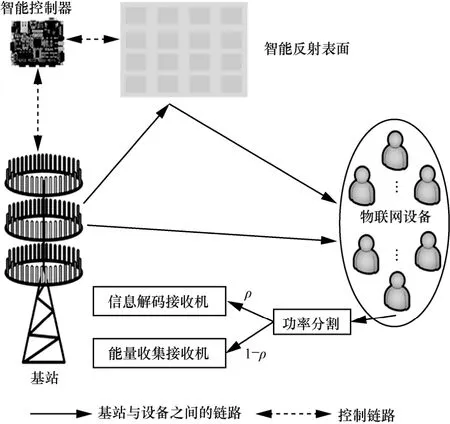
图1 下行智能反射表面辅助的无线携能通信网络

其中，sk为发送给第k个物联网设备的信号，并假定为对应的波束成形矢量。在接收端，第k个物联网设备接收到的信号可以表示为

此外，本文假设每个物联网设备均采用功率分割接收机架构从接收信号中获取信息和能量。每个物联网设备接收到的信号被一个可调的功率分割器分割到信息解码接收机和能量收集接收机。对于第k个物联网设备，将信号功率的ρk∈（0,1）部分用于信息解码，剩余的1-ρk用于能量收集。因此，用于第k个物联网设备的信息解码信号可表示为

因此，在物联网设备k处收到的信干噪比为

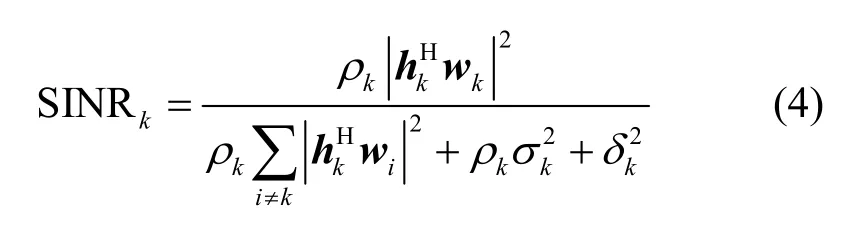
根据式(4)，物联网设备k的数据速率为

除此之外，在能量收集接收机处接收到的信号可以表示为

本文采用线性能量收集模型，在物联网设备k处收集到的能量为

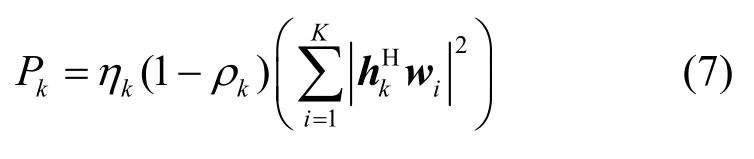
其中，ηk∈(0,1)为物联网设备k的能量转换效率系数。由于噪声功率远小于接收到的信号功率，且能量收集模块必须由接收到的射频信号所携带的相对较高的能量激活（这个能量约为-10 dBm，如果接收到的射频信号所携带的能量低于最小阈值，则不能收集该能量[26]），因此，本文不考虑从噪声功率收集到的能量[27-28]。

基于以上分析，本文通过联合优化基站发射波束矢量、功率分割比和智能反射表面处的相移矩阵，以实现在基站总传输功率、每个设备最小收集能量和相移的单位模约束条件下所有物联网设备的速率和最大化，具体的优化问题可以表示为

其中，Ps表示基站的最大允许发射功率，μk表示第k个物联网设备的最小收集能量门限值。约束条件C1为对发射功率上界的约束。约束条件 C2为每个物联网设备处的能量收集功率约束。约束条件 C3和C4分别为功率分割比约束和智能反射表面上每个元素的相移约束。显然，由于目标函数和约束条件C2、C4的影响，式(8)优化问题是一个多变量耦合、非凸优化问题，不容易直接获得发射波束成形矢量、功率分割比和相移矩阵的最优解。

因此，本文第2 节设计了一种基于块坐标下降的迭代算法来解决以速率和最大化为目标的非凸资源分配问题。

2 算法设计

本节采用块坐标下降法[29]将原始问题解耦成3 个子问题。具体来说，首先，在给定智能反射表面的相移矩阵和功率分割比的情况下，利用连续凸近似方法求解发射波束设计子问题；然后，固定智能反射表面的相移矩阵和发射波束成形矢量，利用连续凸近似优化功率分割比；最后，根据已获得的发射波束成形矢量和功率分割比，利用黎曼流形方法来获取相移矩阵。

2.1 发射波束成形矢量优化

首先，在给定相移矩阵和功率分割比的情况下，优化发射波束成形矢量。同时，令关于发射波束成形矢量的优化问题可以描述为

其中，有

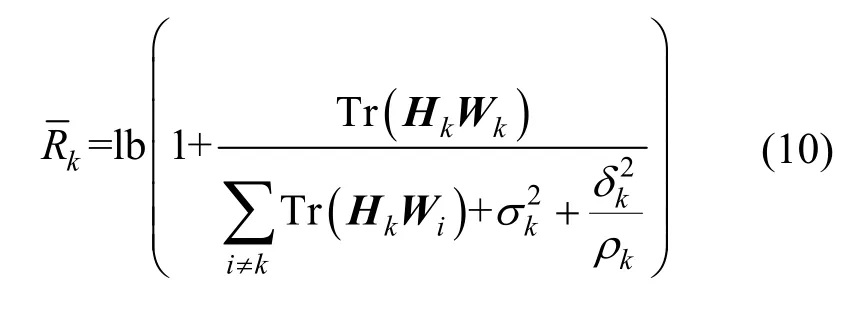
除了约束条件 C5以外，所有约束条件都是凸函数。接下来，处理式(9)中非凸的目标函数。为了方便求解，本文将目标函数写成2 个凸函数之差的形式，即

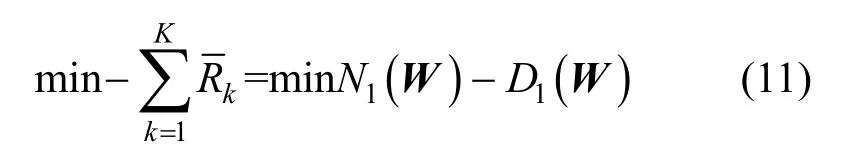
其中，有

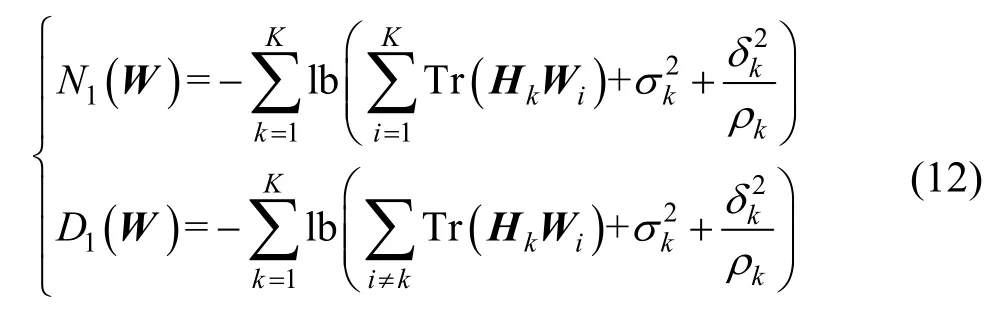
式(11)是关于Wk的凸函数。然而，此时的目标函数仍为非凸的。为了解决这个问题，本文采用连续凸近似方法[30]以迭代的方式获得目标函数的凸上界。因此，本文构造1D的下界，用上标t表示优化变量的迭代指标，即对于任意点利用一阶泰勒展开获得1D的下界，具体表示为

其中，有

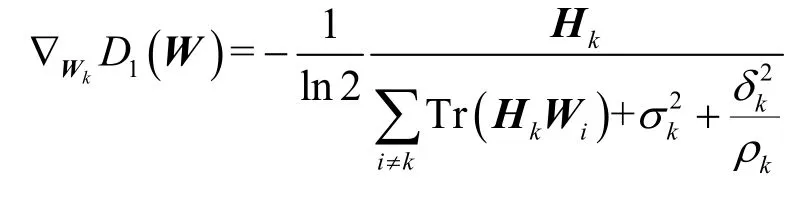
将式(13)引入目标函数式(11)中，可以得到该目标函数的上界。然后，式(9)中唯一剩余的非凸条件是秩约束C5。通常来说，求解秩约束是一个NP 难问题[31]。为了解决这个问题，本文采用半正定松弛方法[32]去掉秩约束C5。因此，式(9)可转化为

算法1基于连续凸近似的算法

2.2 功率分割比优化

接下来，在给定发射波束成形矢量和相移矩阵下，优化功率分割比。式(8)可以转化为

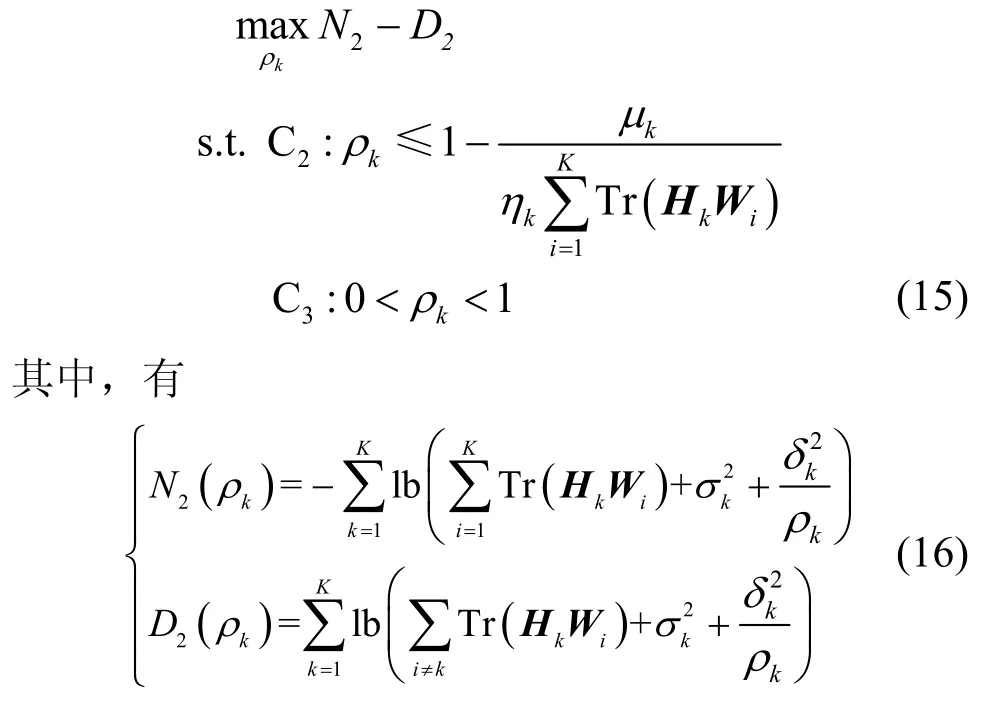
由于N2和2D是关于ρk的凹函数，式(15)属于凹差形式，不能直接求解。因此，与求解发射功率波束成形问题类似，对2D采用一阶泰勒展开，具体表示为

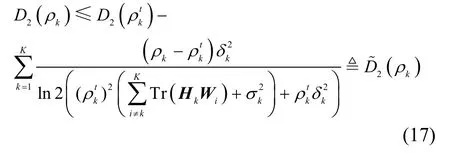
将式(17)引入目标函数式(15)中，则式(15)可以转化为

此时，式(18)问题是凸问题，因此可以采用CVX工具箱对该问题进行求解。

2.3 相移矩阵设计

约束条件 C2可以表示为

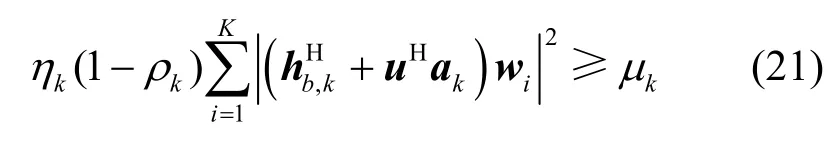
引入一个新的变量αk，则约束条件C2可以表示为

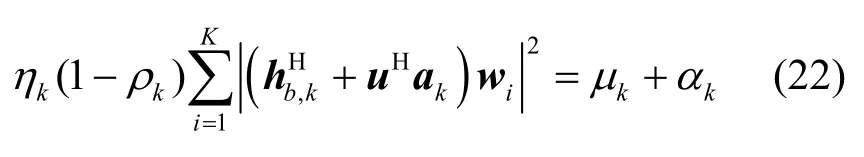
引入新的变量β，β≥0 为罚参数。通过将能量收集约束条件移动到目标函数式(19)中，原来的相移优化问题可以转换为

其中，有

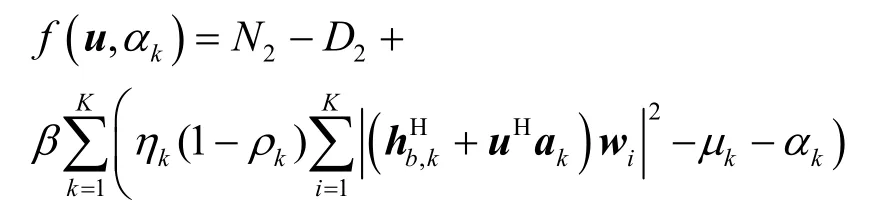
式(23)仍然是非凸的，利用交替优化方法将式(23)问题划分为2 个子问题，即

黎曼流形算法的主要思想是针对式(24)中定义的流形空间执行梯度下降。主要步骤如下。

步骤1求解欧几里得梯度。对于最小化问题，搜索方向是沿着与 (t)f u梯度相反的方向移动，具体方向由式(26)计算获得

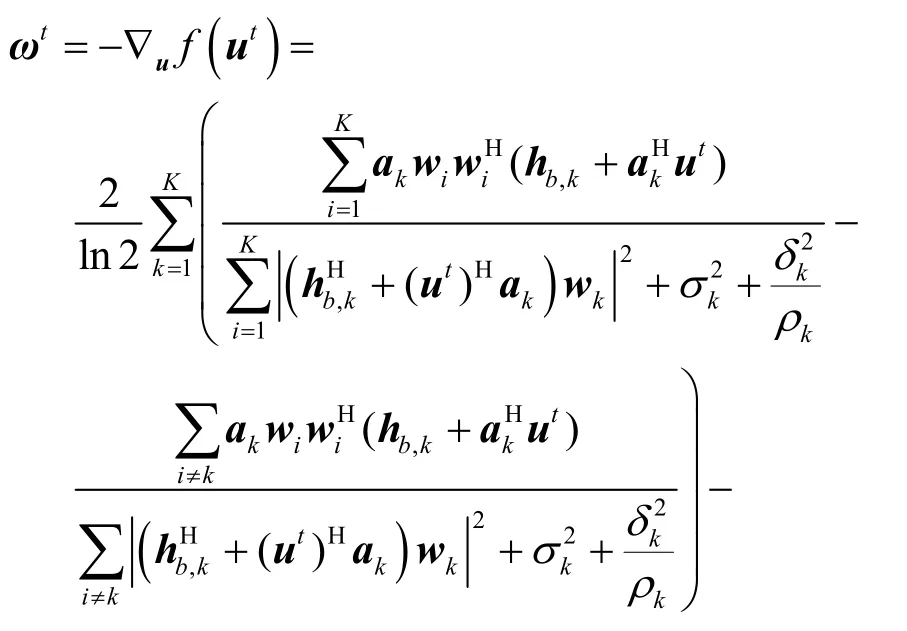
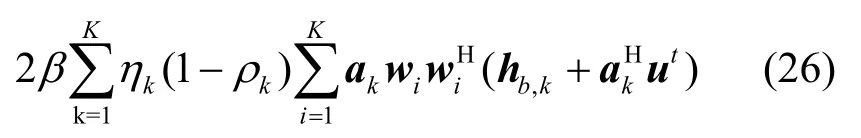
步骤2获得黎曼梯度。f(ut)在当前点ut∈SN的黎曼梯度属于切线空间中。具体来说，通过投影运算将欧几里得空间中的搜索方向投影到切线空间中，可得到f(ut)在ut点上的黎曼梯度为[12]

其中，⊙为哈达玛积。

步骤3更新切线空间。更新切线空间上的当前点ut为

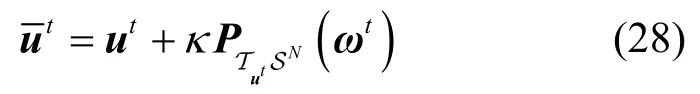
其中，κ为一个常数步长。

步骤4进行回溯运算。由于所获得的不在SN上，因此需要采用回溯运算将该点映射到流形SN上，具体计算式为

其中，ut+1和ut都属于SN，且均满足单位模量约束。具体的黎曼流形算法在算法2 中给出。

算法2黎曼流形算法

定义迭代指数t3=1，给定初始可行解u0，计算式(21)的目标函数；

由于式(24)是凸问题，可以直接进行求解。算法3 总结了本文所提的基于块坐标下降算法。

算法3基于块坐标下降迭代算法

2.4 计算复杂度分析

3 仿真分析

本节通过仿真验证所提算法在智能反射表面辅助的携能通信系统中的性能。假定所考虑的系统由一个基站、一个智能反射表面和4 个物联网设备组成。本文考虑二维坐标系，基站坐标为(0,0)，智能反射表面坐标为(3,3)，物联网设备随机分布在以(5,0)为圆心、5 m 为半径的区域内。此外，所有信道都经历大小尺度衰落，大尺度衰落采用路径损耗模型，即

其中，C0为在参考距离d0=1m 时的路径损耗，d为实际的链路距离。衰落系数取值范围为2～4，在本文中，与智能反射表面相关链路的衰落系数α均设置为2[36]，基站与物联网设备之间链路衰落系数α=2.5。小尺度衰落服从莱斯分布，具体模型为

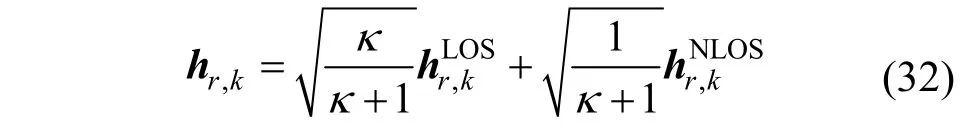
其中，设置莱斯因子κ为5[37]；GNLOS与为非视距部分，服从瑞利分布；GLOS与为视距部分。除非文中单独说明，否则其他仿真参数设置如下：智能反射表面的元素个数为36，基站处发射天线的个数为6 根，能量收集效率系数η=0.8，接收天线处噪声=-7 0dBm，设备信息解码处噪声=-50dBm，基站最大发射功率门限Ps=5W，最小收集能量需求为0.01 mW。

为了验证所提算法的有效性，本文采用以下3 种基准方案进行对比。1) 无IRS 辅助SWIPT的资源分配：不采用IRS，即IRS 处的相移为0，发射波束成形矢量与功率分割比采用本文所提算法获得。2) 配有随机相移的IRS 辅助SWIPT的资源分配：IRS 处的相移采用随机生成的方法，发射波束成形矢量与功率分割比采用本文所提算法获得。3) IRS辅助固定功率分割比SWIPT的资源分配：功率分割比设置为固定值，即ρ=0.5，发射波束成形矢量与相移采用本文所提算法获得。

图2 给出了不同基站发射天线数量、不同IRS 反射单元数量及不同物联网设备数量下，本文所提基于块坐标下降迭代算法的收敛性能。从图2中可以看出，通过本文算法获得的系统速率和首先随着迭代次数单调增加，随后迅速地收敛到某一固定值。此外，随着基站发射天线根数、IRS 反射单元个数及用户设备个数增加，系统性能均有不同程度的提高。当M=8,N=36,K=4时，系统速率和最高。这是因为增加发射天线根数和反射单元个数可以为系统提供更多的空间自由度，提高了系统的阵列增益和分集增益。

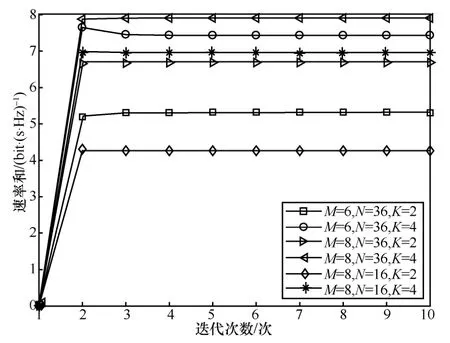
图2 基于块坐标下降迭代算法的收敛性能

图3 给出了不同方案中系统速率和与基站发射功率之间的关系。从图3 可以看出，在每个方案中，系统的速率和都会随着基站发射功率的增加而增大。同时，与无IRS 辅助SWIPT的资源分配相比，本文所提方案（即基于块坐标下降的IRS 辅助SWIPT的资源分配）可以将系统速率和提升近35%。这是因为智能反射表面可以通过调整其上的相移将入射信号反射到物联网设备上，为设备添加了更多的入射路径，进一步改善了基站到设备之间的无线传输环境和设备接收信号功率增益，进而提升了系统的速率和性能。与IRS 辅助固定功率分割比SWIPT的资源分配和配有随机相移的IRS 辅助SWIPT的资源分配相比，本文所提方案在系统速率和性能上有更好的表现。这是因为本文方案进行了多个变量（即基站处波束成形、功率分割比、IRS 处相移）的联合优化，根据需求动态地调整每个变量值，进而得到较好的速率和性能。此外，IRS 辅助固定功率分割比SWIPT的资源分配优于配有随机相移的IRS 辅助SWIPT的资源分配性能，这是因为优化反射相移可以有效地减少多物联网设备间干扰，进而有效地提高速率和性能。而功率分配比的优化主要作用于物联网设备信息速率与收集到能量间的权衡，不能有效地降低物联网设备间的干扰。本文方案可以同时解决多物联网设备间干扰和信息能量权衡问题，因此可以实现更高的速率和性能。

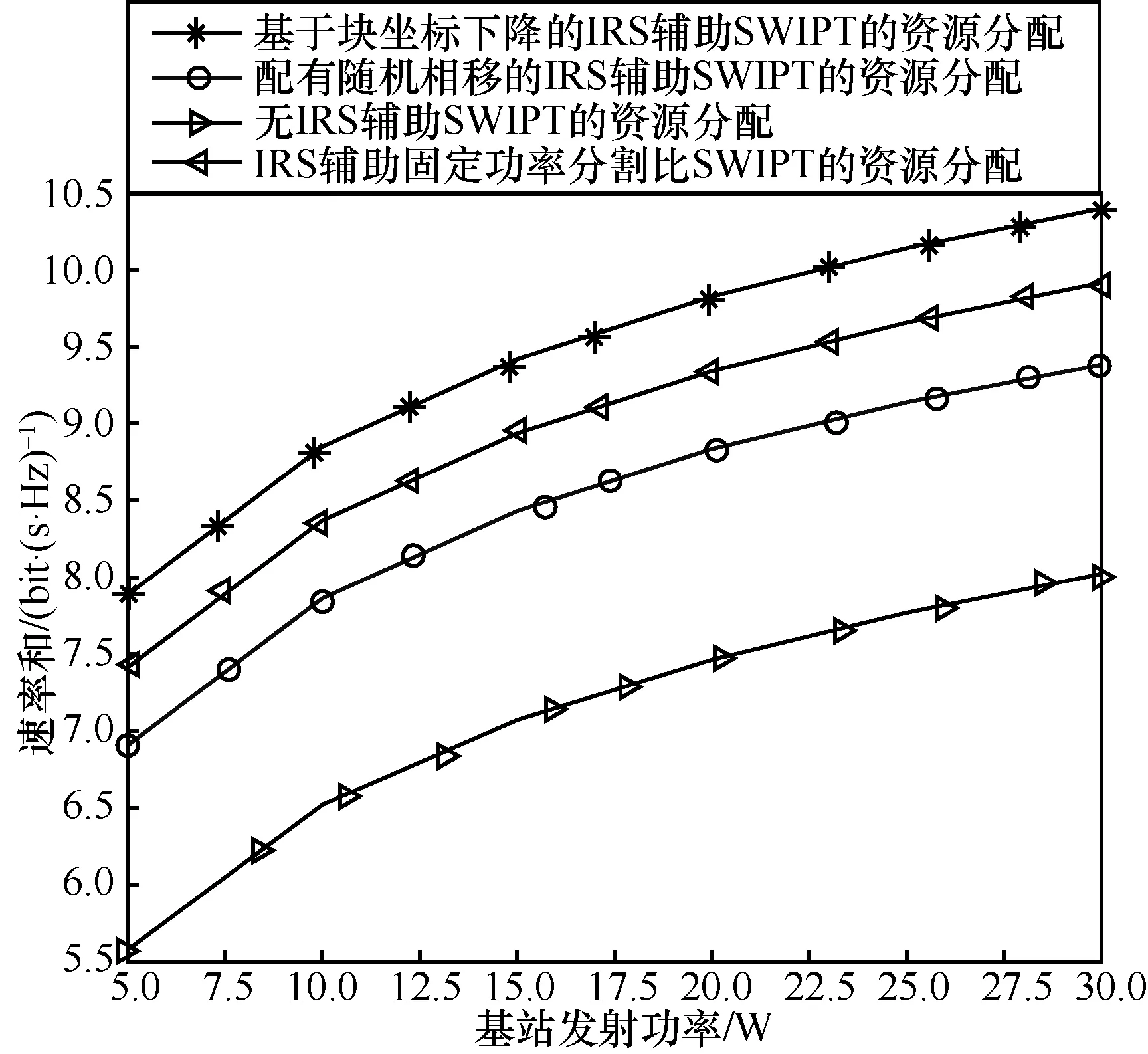
图3 系统速率和与基站发射功率之间的关系

图4 给出了智能反射表面配备不同反射单元个数与速率和之间的关系。从图4 中可以观察到，随着反射单元个数的增加，除了无IRS 辅助SWIPT的资源分配之外，通过其他方案获得的速率和单调增加。这是因为反射单元个数的增加为系统提供了额外的空间自由度，使被动波束成形更加灵活，提高了基站-IRS-物联网设备间链路的信道质量，进而提高了整个系统的速率和。此外，IRS 辅助固定功率分割比SWIPT的资源分配方案和配有随机相移的IRS 辅助SWIPT的资源分配方案性能优于无IRS 辅助SWIPT的资源分配方案，系统的性能增益随着反射单元个数的增加而增大，这也进一步说明了相移优化的重要性。由此证明，将IRS引入SWIPT系统是有必要的。

图4 不同反射单元个数与速率和之间的关系

图5 给出了系统速率和与最小能量收集门限的关系。从图5 可以看出，本文所提方案的性能仍优于其他3 种方案。随着设备收集能量需求的增加，整个系统的速率和呈现下降趋势。这是因为系统速率和与设备收集能量之间存在权衡关系。为了满足较高的能量收集要求，物联网设备侧降低了分配给数据传输所用的功率，进而导致系统的数据速率和降低。以基于块坐标下降的IRS 辅助SWIPT的资源分配为例，性能下降的斜率约为0.008 3（最小能量收集以μW 为单位计算），而无IRS的资源分配方案下降的斜率约为0.01。采用IRS的资源分配方案，下降趋势较缓慢，其原因是通过调整大量的反射元件可以补偿一部分信道条件，提高物联网设备处的接收功率，使其可以收集到更多的能量。此外，随着物联网设备处最小收集能量值的增加，IRS 辅助SWIPT的资源分配方案与无IRS 辅助SWIPT的资源分配方案之间差距增大。由此可以说明，引入IRS 对物联网设备所需的最小能量收集量提供更多的包容性。

图5 速率和与最小能量收集门限的关系

4 结束语

为实现未来的绿色万物高效互联，本文对智能反射表面辅助的无线携能通信网络中的发射波束设计、功率分割比决策及相移设计进行了研究。考虑基站发射功率限制、所有设备最低能量需求限制和相移约束，建立以速率和最大化为目标的多维资源联合分配模型。利用块坐标下降法把所建模的优化问题解耦成3 个子问题，利用连续凸近似方法分别求解发射波束设计和功率分割比决策2 个子问题，利用黎曼流形方法求解智能反射表面相移设计子问题，并分析了所提算法的计算复杂度。仿真结果表明，本文所提方案在不同场景和条件下，相比于现有方案，均可获得较高的系统速率和。