类Piccolo 结构的差分安全性评估

王念平，殷勍

（1.信息工程大学密码工程学院，河南 郑州 450004；2.航天工程大学，北京 101416）

0 引言

分组密码作为现代密码学的重要组成部分，在信息安全领域有着广泛的应用。分组密码具有易于标准化、便于软硬件实现和容易同步等优点[1-2]，但也有一定的缺陷。例如，分组密码不能隐蔽数据模式，即相同的密文蕴含着相同的明文组，这是因为分组密码使用的是一个不随时间变化的固定变换。同时，分组密码不能抵抗组的重放、嵌入和删除等攻击。但上述的缺陷可以通过在加密过程中引入少量记忆加以克服，例如，可以通过密码分组链接（CBC,cipher block chaining）方式来克服[2-3]。另外，分组密码的安全性很难被证明。尽管“可证明安全性”的研究发展很快，但目前的分组密码大多是“看起来安全”的，还没有哪一个著名的分组密码真正被证明是安全的，至多证明了局部安全性。

对于分组密码，目前还存在一些问题值得考虑。一是分组密码算法的标准化。分组密码的大量社会化应用呼唤密码算法的标准化。二是分组密码设计和分析理论的研究。作为分组密码的研究者，总是希望从理论上解释一些设计方法的合理性，并将一些分析方法理论化，而不仅仅是停留在设计经验和直观分析的层次上。例如在一定假设条件下的可证明安全性和伪随机性常常是研究者追求的一个目标。三是分组密码安全性分析的自动化。这是计算机技术与密码分析的有机结合。将一些密码分析方法程序化，往往可以提升分析的深度，弥补手工分析的不足。四是分组密码算法评估的实用化。算法的评估不仅要考虑在传统数学模型下的安全性，还应结合实现和应用环境评估算法的安全性，例如在侧信道模型下的安全性。本文的研究属于第二项内容。事实上，分组密码的整体结构对分组密码的安全性有很大影响。因此，研究分组密码结构的安全性一直是分组密码研究领域的重要内容。

差分密码分析[4]是一种典型的分组密码分析方法。差分密码分析能否成功主要取决于所利用的差分特征概率的大小。文献[5]指出，在最大差分特征概率足够小的情况下，就认为该密码算法对差分密码分析是免疫的。但在现实中，计算最大差分特征概率有一定的困难，且较难实现，所以就退而求其次——计算最大差分特征概率的上界，而最大差分特征概率的上界的计算取决于活动轮函数或活动S盒个数的下界。需要指出的是，在计算差分特征的活动轮函数或活动S 盒个数的下界时，一般并不考虑轮函数和S 盒的具体细化结构，而只是假设它们是双射的即可，从而所得的结果更具普遍性。文献[6-9]就是基于这样的思路进行分析的。

Piccolo 结构[10-11]是从Piccolo 算法[12]中归结出来的一种密码结构，如图1 所示。其设计特点在于块移位变换RP 不直接对4 个分块Y0、Y1、Y2、Y3进行移位，而是对平均分成的8 个子分块进行移位。文献[10]研究了Piccolo结构抵抗差分密码分析的能力，证明了k(k≥ 1)轮差分特征至少有k-1个活动轮函数和(n+1)(k-1)个活动S 盒（n+1是轮函数中P 变换的差分分支数）。文献[11]改进了文献[10]中的结果，证明了k(k≥ 6)轮差分特征至少有k个活动轮函数和(n+1)k个活动S 盒，并指出活动轮函数个数的下界结果是不可改进的，所谓不可改进，是指确实存在一类差分特征，其活动轮函数的个数恰好达到了给出的下界。本文在此基础上，提出32 种类Piccolo 结构（包括文献[10-11]中的Piccolo 结构），并对这些类Piccolo 结构进行了差分密码分析，给出了活动轮函数和活动S 盒个数的一个下界。

图1 Piccolo 结构

本文的结果与文献[10-11]相比，改进之处在于文献[10-11]只是针对Piccolo 结构这一种密码结构进行分析的，而本文是针对提出的32 种类Piccolo结构进行分析的。本文的结果比文献[10]中的结果要好，比文献[11]中的结果更具一般性。

1 预备知识

1.1 基本概念

定义1[13]设(X,+)和(Y,+)都是有限交换群，f:X→Y,α∈X,β∈Y，差分概率p f(α→β)定义为

其中，“| · |”和“#{·} ”表示集合的基数。

定义2[1]r(r≥ 1)轮差分特征Ω是一个差分序列α0,α1,…,α r，其中α0是明文对Y0和的差分，αi(1≤i≤r)是第i轮输出Yi和的差分。

定义3[14]输入差分非零的轮函数（S 盒），称为活动轮函数（S 盒）。

定义4r(r≥1) 轮差分特征中活动轮函数的个数称为该差分特征的活动指标。

本文称r(r≥1) 轮差分特征的活动指标为r(r≥1) 轮Piccolo 结构的活动指标。本文中，将n元块移位变换简记为 (i0i1···in-1)，它表示按从左到右的顺序将原来第ij个分块aij移动到第j(j=0,1,…,n-1)个分块的位置，即

1.2 类Piccolo 结构描述

图2 类Piccolo 结构

表1 集合A

表1 中，8 元块移位变换 (i0i1···i7)表示移位变换（下同）。

1) 轮函数f0,1f

如图3 所示，轮函数f0,1f都采用SPS 结构，这里S 表示n个m×m双射S 盒（n为偶数且nm=t，t为输入块X i(i=0,1,2,3)的比特数），P 表示的线性变换x→Mx，M表示有限域GF(2m) 上的n阶MDS 矩阵。易知，P 变换的分支数（包括差分分支数和线性分支数[13]）为(n+1)，且轮函数f0,1f都是双射。

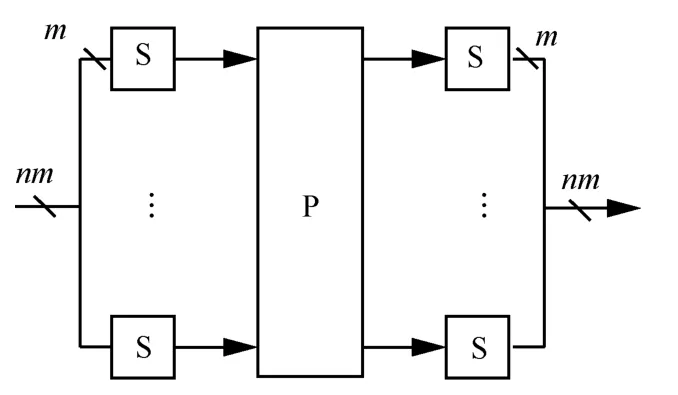
图3 轮函数

2) 块移位变换σ

集合A中的8 元块移位变换是满足以下2 个条件的置换。

条件1ij∈{2,3,6,7},j=0,1,4,5；ik∈{0,1,4,5},k=2,3,6,7。

形象地说，满足条件1的σ如图4 所示，即i j(j=0,1,4,5)只能从 {2,3,6,7} 中选取，ik(k=2,3,6,7)只能从{0,1,4,5}中选取。

图4 满足条件1的σ

形象地说，满足条件2的σ如图5 所示，即将每个大块2i2i+1 中的2 个小块2i和2i+1 分别移位到不同的大块中去。

图5 满足条件2的σ

条件1 和条件2 共同保证了类Piccolo 结构的扩散效果。

备注1为了叙述方便，将块移位变换是σ的类Piccolo 结构称为σ-Piccolo 结构。

2 类Piccolo 结构的活动轮函数和活动S 盒个数的下界

为了分析方便，将X i(i=0,1,2,3)看成由左右规模相等的两部分x2i和x2i+1连接而成，即X0=x0||x1,X1=x2||x3,X2=x4||x5,X3=x6||x7，其中“||”表示比特块的连接。那么，类Piccolo 结构的输入就可表示为(x0||x1,x2||x3,x4||x5,，一轮类Piccolo 结构（略去子密钥）的输入和输出关系式就可表示为

首先，给出σ-Piccolo 结构的差分对应的结构形式。

定理1对任一σ-Piccolo 结构，设具有非零概率的一轮差分对应都具有如下形式

证毕。

由定理1，可得以下事实。

引理2对于任一σ-Piccolo 结构，以下3 个结论成立。

结论1一轮Piccolo 结构的活动指标大于或等于0。

结论22 轮Piccolo 结构的活动指标大于或等于1。

结论33 轮Piccolo 结构的活动指标大于或等于2。

证明1) 结论1 显然成立，只证结论2 和结论3。

由备注2 知，活动指标与最后一轮输出差分无关，从而为书写方便，有时将差分特征的最后一轮输出差分记为(* || *,* || *,* || *,* || *) 。

2) 由定理1，设σ-Piccolo 结构的2 轮差分特征为

3) 由定理1，设σ-Piccolo 结构的3 轮差分特征为

综合情形1 和情形2，引理2 成立。证毕。

接下来，设(α0||α1,α2||α3,α4||α5,α6||α7)是σ-Piccolo 结构的输入差分。若差分块αi为非零差分块，则用“1”表示；若差分块αi为零差分块，则用“0”表示，其中i=0,1,2,…,7。那么，σ-Piccolo结构的非零输入差分恰好有28-1=255 种表示，即Δ1=(10000000),Δ2=(01000000),…,Δ255=(11111111)（这种表示方法不妨称为“0”“1”表示）。易知，f0为活动轮函数当且仅当左起第1、2 位不全为零，f1为活动轮函数当且仅当左起第5、6 位不全为零。

首先，给出输入输出差分块“0”“1”进行XOR运算需要满足的运算规则：设a,b,c,d∈{0,1}分别是按照上述方法的“0”“1”表示，且设“∧”是按位与，“∨”是按位或。

性质2差分经过XOR 运算需要满足以下条件：设α⊕β=γ，则

性质2 表示对于α⊕β=γ，当α,β至少有一个为零时，有c=a+b；当α,β都非零时，α⊕β=γ的值可能为零，也可能不为零，所以c=0或1。

性质3差分经过轮函数需要满足以下条件：设f(α||β)=γ||δ，则

性质3 表示当轮函数的输入差分非零时，有a+b+c+d≥ 3（因为输入差分和输出差分满足性质1）；当轮函数的输入差分为零时，输出差分也为零。

根据性质2 和性质3，借助计算机，可以完成以下3 个实验。

实验1计算机搜索32 个σ-Piccolo 结构，给出所有第一轮的活动指标为0、第2 轮的活动指标为1、第3 轮的活动指标为1的3 轮差分特征的尾轮输出差分（二进制）。

实验1的具体结果如表2 所示。通过表2 发现，对于任一满足条件的3 轮差分特征的尾轮输出差分x0和x1至少有一个为“1”，和5x至少有一个为“1”，故可得以下结论。

表2 实验1的具体结果

命题1对于任一σ-Piccolo 结构，设4 轮差分特征满足第一轮的活动指标为0，第2 轮的活动指标为1，第3 轮的活动指标为1，则第4 轮的活动指标必为2。

引理3对于任一σ-Piccolo 结构，当输入差分具有(0||0,α2||α3,0||0,α6||α7)形式时，以下3 个结论至少有一个成立。

结论1前2 轮Piccolo 结构的活动指标大于或等于2。

结论2前3 轮Piccolo 结构的活动指标大于或等于3。

结论34 轮Piccolo结构的活动指标恰为4。其中，α2||α3,α6||α7不全为零。

证明只需证明结论1 和结论2 都不成立时，必有结论3 成立即可。由引理2 知，2 轮Piccolo 结构的活动指标大于或等于1，3 轮Piccolo 结构的活动指标大于或等于2，从而只需证明前2 轮Piccolo结构的活动指标为1，且前3 轮Piccolo 结构的活动指标为2时，必有结论3成立即可。

定理2对于任一σ-Piccolo 结构，k(k≥ 1)轮Piccolo 结构的活动指标大于或等于k-1。

证明（数学归纳法）当k=1,2,3时，由引理2知，定理2 成立。

假设k＜l(l≥ 4)时定理2 成立，以下证明k=l时定理2 成立。

此时，由引理3，又可分为3 种情形。

综合情形1 和情形2，定理2 成立。证毕。

实验2计算机搜索32 个σ-Piccolo 结构，给出6 轮Piccolo 结构的活动指标的最小值。

因篇幅所限，这里只以块移位变换σ=(72503614)为例给出实验2的结果，具体如表3所示。其中第x（十六进制）行第y（十六进制）列交叉处的数值表示以(x y)为首轮输入差分的6 轮Piccolo 结构的活动指标的最小值。例如，第3 行第e 列交叉处的数值为6，就表示以为首轮输入差分的6 轮Piccolo 结构的活动指标的最小值为6。这里，行数和列数都从0 开始计算，另外，实验结果表明，使活动指标的最小值为6的6 轮Piccolo 结构的非零输入差分共有67个，使活动指标的最小值为7的6 轮Piccolo 结构的非零输入差分共有164 个，使活动指标的最小值为8的6 轮Piccolo 结构的非零输入差分共有24 个。

表3 实验2的结果

实验2 结果表明，有以下结论成立。

命题2 对于任一σ-Piccolo 结构，6 轮Piccolo结构的活动指标大于或等于6。

实验3对于任一σ-Piccolo 结构，利用计算机筛选出活动指标为6的6 轮差分特征的尾轮输出差分（十六进制），筛选出活动指标恰为k-1(k=1,2,3,4,5)的k轮差分特征的首轮输入差分（十六进制）。

实验3的具体结果如表4 所示。通过观察表4发现，对于任一σ-Piccolo 结构，实验3 中所求的尾轮输出差分和首轮输入差分没有重合，故可得以下结论。

表4 实验3的具体结果

命题3对于任一σ-Piccolo 结构，若6 轮Piccolo 结构的活动指标为6，则它的后面不可能“联接”活动指标为k-1(k=1,2,3,4,5)的k轮差分特征。

引理4对于任一σ-Piccolo 结构，设为任一活动指标为6n的6n轮差分特征，则最后6 轮差分特征的活动指标必为6。

证明根据命题 2 可知，6 轮差分特征α(6n-6)→…→α(6n)的 活动指标≥ 6。若α(6n-6)→…→α(6n)的活动指标大于6，则6(n-1)轮差分特征α(0)→α(1)→ …→α(6)→ …→α(6n-6)的活动指标必小于6(n-1)，这与命题2 矛盾，故α(6n-6)→ …→α(6n)的活动指标必为6，引理4 成立。证毕。

定理3对于任一σ-Piccolo 结构，以下2 个结论成立。

结论1k(1≤k≤ 5)轮Piccolo 结构的活动指标大于或等于k-1。

结论2k(k≥ 6)轮Piccolo 结构的活动指标大于或等于k。

证明1) 结论1 由定理2 即可证明。

2) 当k=6n(n≥ 1)时，由命题2 可知，结论2成立。当k=6n+m(n≥ 1,1≤m≤ 5)时，分以下2 种情形进行讨论。

情形1前6n轮Piccolo 结构的活动指标大于或等于6n+1。

此时，由定理 2 可知，后m轮差分特征α(6n)→…→α(6n+m)的活动指标大于或等于m-1，所以6n+m轮Piccolo 结构的活动指标大于或等于(6n+1)+(m-1)=6n+m。

情形2前6n轮Piccolo 结构的活动指标恰为6n时。

此时，设α(0)→ …→α(6n)→ …→α(6n+m)为任一6n+m轮差分特征，且6n轮差分特征α(0)→…→α(6n)的活动指标为6n。由引理4 知，α(6n-6)→ …→α(6n)的活动指标为6，再由命题3 和定理2可知，后m轮差分特征α(6n)→ …→α(6n+m)的活动指标大于或等于m，所以6n+m轮Piccolo结构的活动指标大于或等于6n+m。

综合情形1 和情形2，定理3 成立。证毕。

由定理3 可得以下推论（注意：轮函数中的P变换的差分分支数为n+1 ）。

推论1对于任一σ-Piccolo 结构，以下2 个结论成立。

结论1k(1≤k≤ 5)轮差分特征中活动S盒的个数大于或等于(n+1)(k-1)。

结论2k(k≥ 6)轮差分特征中活动S 盒的个数大于或等于(n+1)k。

3 结束语

本文提出了类Piccolo 结构，并通过对差分传递规律的分析，得到了多轮类Piccolo 结构的活动轮函数和活动S 盒个数的一个下界。利用这些结果，结合轮函数或S 盒的最大差分概率，给出类Piccolo 结构的最大差分特征概率的上界。本文的研究结果对分组密码的设计与分析具有较大的指导意义，但类Piccolo结构抵抗其他攻击的能力如何值得进一步研究。