基于系统响应时间的云服务质量评估模型

杨喆曦 薛华成

1(中国计量大学标准化学院 浙江 杭州 310018)

2(复旦大学管理学院 上海 200433)

基于系统响应时间的云服务质量评估模型

杨喆曦1薛华成2

1(中国计量大学标准化学院 浙江 杭州 310018)

2(复旦大学管理学院 上海 200433)

响应时间是云服务系统的主要质量衡量指标之一，过长的系统响应时间意味着用户的流失。以队列等待、服务器处理时间和网络延迟构成云访问的总体响应时间，采用嵌入马尔可夫链的方法生成观察点的马尔可夫链。借助马尔可夫链的无后效特性来模拟云访问的随机到达，以此为基础构建云服务排队模型，用以评估云服务质量。通过解析仿真的方法验证了所提出的云服务质量评估模型的有效性。

云计算 响应时间 排队论 马尔可夫链

0 引 言

云计算服务将大量的软硬件资源整合起来统一提供给各种类型以不同形式随机出现的用户[1]，从这个意义上说对云计算服务系统服务质量(QoS)的研究类似于对排队服务系统服务质量(服务时间、等待时间、队列长度等指标)的研究。鉴于云计算对资源的高度集成与对用户使用的透明性，云计算服务系统是一个单服务台的服务系统[2]。然而基于云计算的分布式、网格化基石，云计算服务系统又是一个可以具有无限多服务台的服务系统[3-4]，因此云计算系统的QoS评价与衡量可以集中于对单个服务台(主机或虚拟机)及其网络传输QoS的评价与衡量。但是服务水平是一个难以量化的抽象指标，而简单的队列长度难以有效衡量排队服务系统的服务质量，采用顾客在系统中的逗留时间或队列中的等待时间能够对服务系统质量进行直观量化，便于进行对比和分析。

1 云服务排队系统与传统排队系统的区别

1.1 虚拟化

虚拟化是云计算的核心技术和主要特征，因此基与云计算的排队系统也必然是虚拟化的。分布在网络各地的访问请求被云服务系统统一进行受理，从云服务系统庞大的硬件资源群中为请求分配特定的软、硬件资源[5]。因此，云服务系统中所有服务都是在云资源虚拟化的基础上提供的，访问所获取的资源都是虚拟机，受理访问的服务台都是虚拟机。

1.2 多源访问

服务系统的顾客不是传统的有形客户或无形电话呼叫，而是Web Application或其他应用程序所发出的访问请求。这种访问请求可能是终端用户触发的，也可能是由应用程序生成的，因此云服务系统中访问请求的来源多种多样[6]。

1.3 并行访问

传统的排队服务系统一个服务台一次只受理一个顾客的访问，而鉴于计算机处理的分时并行机制，云计算环境中一个虚拟机也能够经常同时响应多个访问请求，这与传统排队理论服务规则不一致[7-8]。

1.4 峰、谷访问

云服务系统部署在云端，供用户365×7×24进行访问，对于特定的用户群，由于工作习惯、业务流程、时区差异等原因存在一定的高峰访问时间和低谷访问时间。峰、谷的差异对云服务系统设计和成本控制都具有重要的意义。

1.5 协同处理

为了提高云服务效率，访问请求通常会被任务分派器进行切割、分块处理，因此云计算的单个访问请求往往都是在不同的虚拟机、物理机上单独处理。然后通过协同、组装等方式形成完整的处理结果[9]。

1.6 灵活的服务台设置

信息技术的飞速发展导致的硬件成本飞速下降使得云服务系统的主机设置能够根据需要以低廉的成本进行动态增减，对所有软硬件资源进行集成的云平台也能够支撑主机的动态增减。同时虚拟机技术的成熟能够动态申请和销毁虚拟机，从而使得云服务系统中服务台因素不是设计者考虑的首要问题[10]。

尽管与传统的排队服务系统相比有许多的差异，但这些差异都可以通过适当变通转换为经典的排队服务系统模式。因此，云服务排队系统仍然是一个典型的排队系统，排队理论中的相关定理与结论仍然适用。

2 云服务排队系统主要性能指标

在云计算的服务队列规则中，不考虑顾客的损失，而一律采取等待的方式。终端客户通过Web Application 或其他接口向云端提交访问请求后等待访问结果的过程就是排队等待的过程。根据相关研究，客户等待访问结果的最大时间通常是4到6秒，超出这个时间客户将会因极度失望离开，在意味着客户流失的同时也意味着云服务系统服务水平的低下。

从云客户的角度而言，自访问请求被提交开始到得到处理结果的整个等待过程都是客户等待云服务系统响应的等待时间，以系统中云客户整体等待时间W代表云服务系统的服务水平。由于云服务系统是一个超级计算机，能够同时对成千上万的访问请求进行及时响应，因此在只有一个数据中心的情况下可以将云服务系统看成n个并行、独立的服务台(虚拟机)。服务台只有在进行了任务分配后才与请求建立了对应的服务关系，否则两者没有任何关联[11]。因此，以所有服务台中顾客等待时间的均值为整个服务系统整体等待时间，用以代表其云服务的整体服务水平。令云系统服务水平为：

(1)

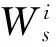
对云客户而言，访问请求一旦提交，后续的工作都是云服务提供商负责的内容。因此访问提交后的信息传递的网络延迟，队列等待和请求处理耗时都是顾客等待云服务系统响应的耗时，是云客户衡量云服务质量优劣的直观指标，也是企业构建云服务时需要参考和实现的重要目标。根据式(1)的描述，云服务系统服务水平的参数主要包括逗留时间和网络延迟，而逗留时间又包括队列等待时间和服务处理时间。

2.1 基于马尓可夫链的等待时间

由于顾客达到和服务时间都具有随机性，因此基于其上的这些数量指标均为随机变量。这些指标的瞬态特征对排队系统的各项特性不具有说服力，通常我们只对统计平稳状态下的稳态数量指标感兴趣。所以在定量分析排队系统的性能时，通常是指分析系统在平衡状态下的性能。对云客户的使用感受而言，除去网络传输耗时，衡量一个云服务系统的质量好坏主要依据其提交访问请求后得到服务结果的等待时间，即云服务系统的响应时间。

鉴于从云资源管理系统到虚拟机的任务信息传递时间已经包括在下文描述的网络延迟时间中，且无论采用什么样的排队模式都不影响这个时间的取值。因此本文对于队列等待时间的研究可以抛开排队模式的差异而只研究在任务响应端的虚拟机及其前面排队等候处理的任务队列的处理情况。

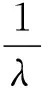
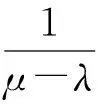
(2)

虽然在用户的眼里，云服务系统似乎是一个单服务台的排队服务系统，然而以其庞大的服务能力而著称的云中心实际上拥有无限多虚拟机可以响应用户的请求。因此，结合排队论相关定理，对于多服务台(服务台个数为k)排队系统而言，有平均逗留时间计算公式：

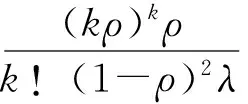
(3)

而相应的队列平均排队时间计算公式为：

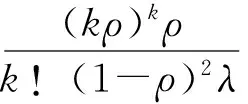
(4)

其中：

(5)

式(3)就是式(1)的一个特殊形式，刻画的是一个多任务台的云服务系统对所有抵达请求不加歧视的统一进行处理的情况。

本文采用嵌入马尔可夫链来更贴切模拟访问请求的到达行为和规律，而不只是简单的采用Poisson流的方式。马尔可夫链(也叫马氏链)是用来描述离散事件随机过程最常用的一个模型，由于所具有的无后效性而被广泛使用。嵌入马氏链技术要求对可观察的系统状态进行一些列马氏点选择，然后在访问请求刚好到达之前对这些任务点(包括正在服务中的和队列中还未被服务的任务)进行编号，如0，1，2，…，这样我们就得到了一个同质的马氏链。在这个嵌入的马氏链中得到的是每次访问请求到达前的系统状态,如图1所示。

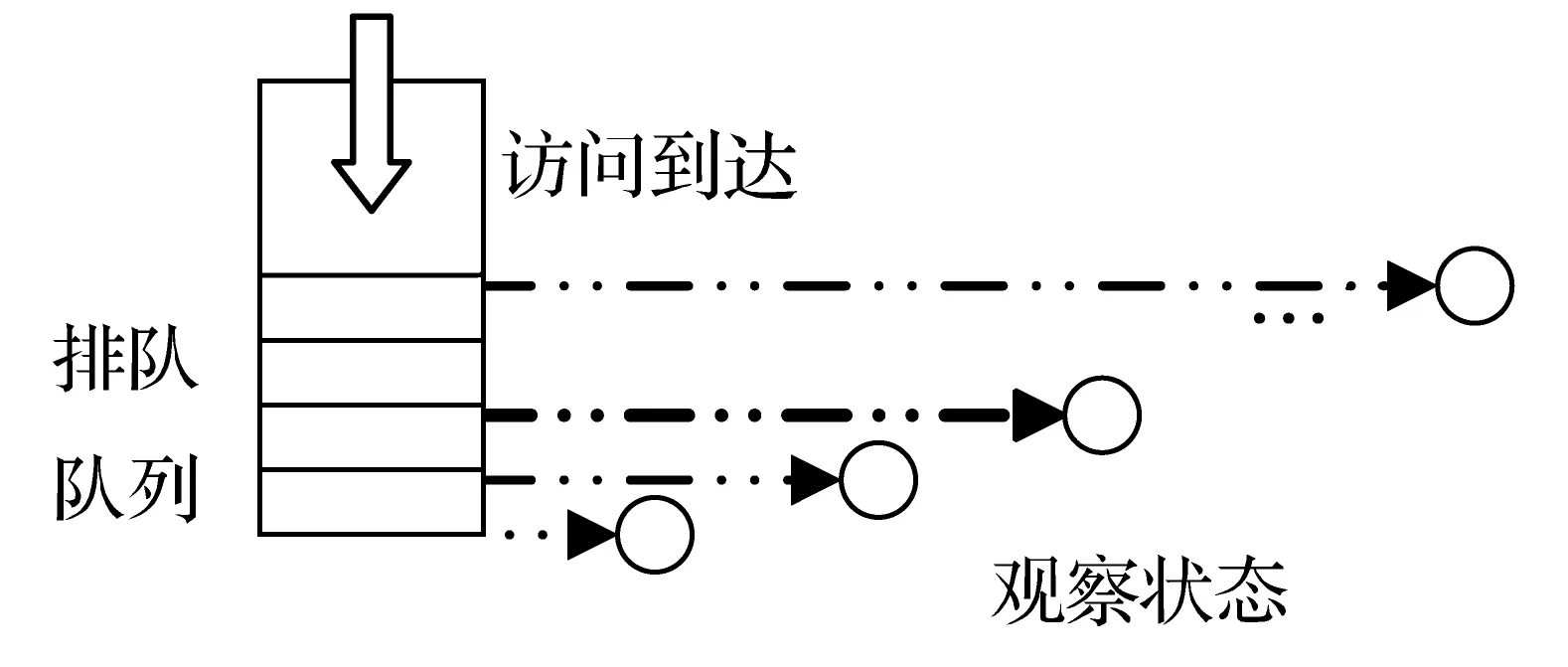
图1 嵌入马氏链观察点示意图

访问请求的到达仍然假设为服从Poisson分布，每个任务都有一个虚拟机负责进行响应，从而嵌入马氏链的过程如图2所示。

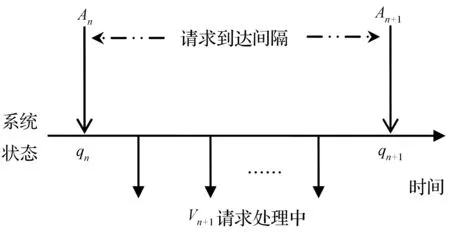
图2 嵌入马氏链过程示意图

图2中An和An+1表示云服务系统第n个和n+1个访问请求到达系统的时刻，相应的qn和qn+1分别表示对应到达时刻系统中包括在处理和在等待任务在内的任务数。令vn+1表示从An到An+1时刻系统处理完的任务数，从而有如下等式：

qn+1=qn-vn+1+1

(6)

马氏链的状态转换概率可以定义为：

pi,j=Prob[qn+1=j|qn=i]

(7)

式(7)表示i+1-j个请求在两个成功抵达任务间隔被响应的概率。显然对于j>i+1时的概率Pi,j=0。

A到达间隔时间的Laplace Stieltjes 变换(LST)为：

(8)

服务时间B的LST为：

(9)

残存服务时间是从服务时间中任一点(Poisson流的一个达到点)到服务结束的时间间隔，将其表示成B+，已过任务服务时间是自服务开始到任一点的服务时间间隔，将其记作B_。任务在下次请求到达前被完成的基本条件是其处理时间小于请求到达间隔，因此其概率可以写成：

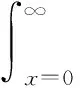
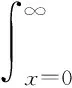
(10)

当恰好有空闲服务台时，抵达请求就能立即被受理，这个请求在下一个请求到达前被受理完成的概率Py计算如下：

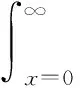
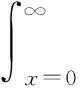
(11)

而当队列任务到达非空时，会发生如下几种情况。如果两个成功到达间隔中有任务完成，服务台会从该非空队列中提取一个新任务。而如果这个新任务依然在下次请求到达前完成，服务台再从非空队列中提取新任务，以次类推指导队列为空或有新请求到达。因此在队列中有足够任务提取的情况下，服务台有k(>0)个任务在下次请求到达前完成的概率根据式(10)和式(11)有：

(12)

在稳态状态下，设W(x)和W×(s)为服务等待时间W的CDF和LST，从而

(13)

其中π=[π0,π1,π2,…]是稳态概率。

2.2 基于处理器模式的处理时间

IT技术的飞速发展早已使计算机摆脱了单核时代，步入双核、四核乃至更先进的多处理器时代。这种多处理器的硬件设备也引发了处理器进行任务响应上的策略差异。云计算的虚拟机技术中，在处理器的任务处理方式上有两种处理策略[7]:空间共享与时间共享。虚拟机的空间共享就是将虚拟机的任务按时间先后来进行执行，虚拟机的时间共享就是把所有虚拟机的请求分配给每个处理器；任务的空间共享就是将多个处理器看作一个处理器，从而将一个任务分配多个处理器上，任务的时间共享就是每个处理器的一个时间片上响应两个虚拟机的请求。即虚拟机的空间共享就是在任一时刻，只有一个虚拟机能够运行，从而任务也是逐一被执行；虚拟机的时间共享就是任一时刻，都有多个虚拟机的任务请求被响应，从而任务都被同时响应[12]。因此总共就有4类策略组合方式，对于双核双虚拟机的情况，恰好有图所示的4种策略组合：CPU空间共享-任务空间共享或叫完全空间共享(见图3)，CPU空间共享-任务时间共享(见图4)，CPU时间共享-任务空间共享(见图5)，CPU时间共享-任务时间共享或叫完全时间共享(见图6)。为了很好地说明这两种处理策略的异同，以一个双核CPU的设备为例，假设云计算服务申请了两个虚拟机也同时接收用户的服务请求。其中VM1的服务请求由t1～t4组成，VM2的服务请求由t5～t8组成，不同的处理策略在处理器中处理时间分配方式和任务执行顺序上存在差异。

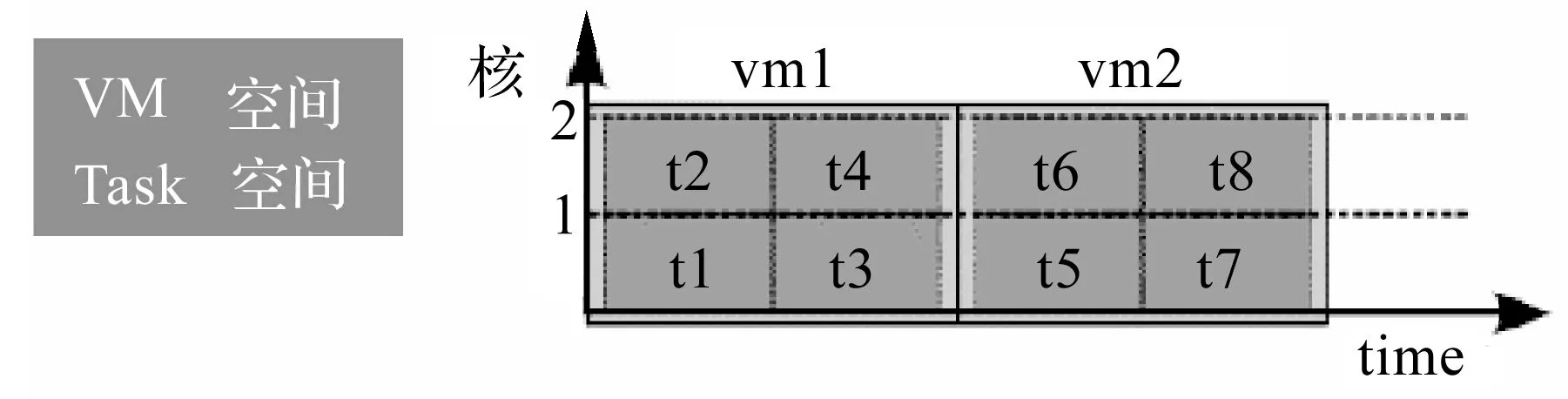
图3 处理器任务处理策略a

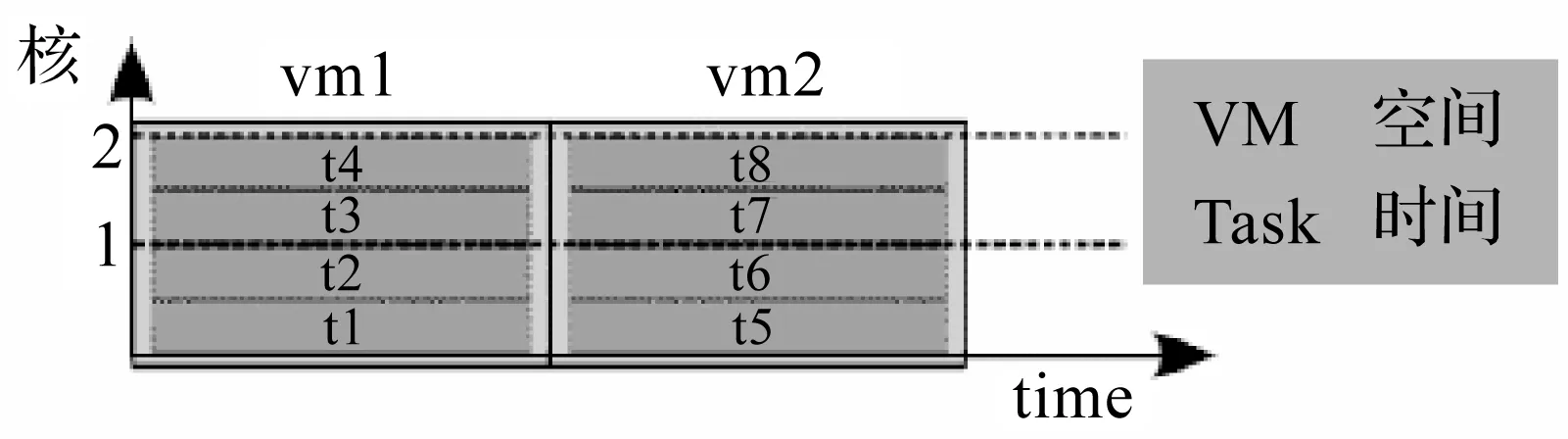
图4 处理器任务处理策略b

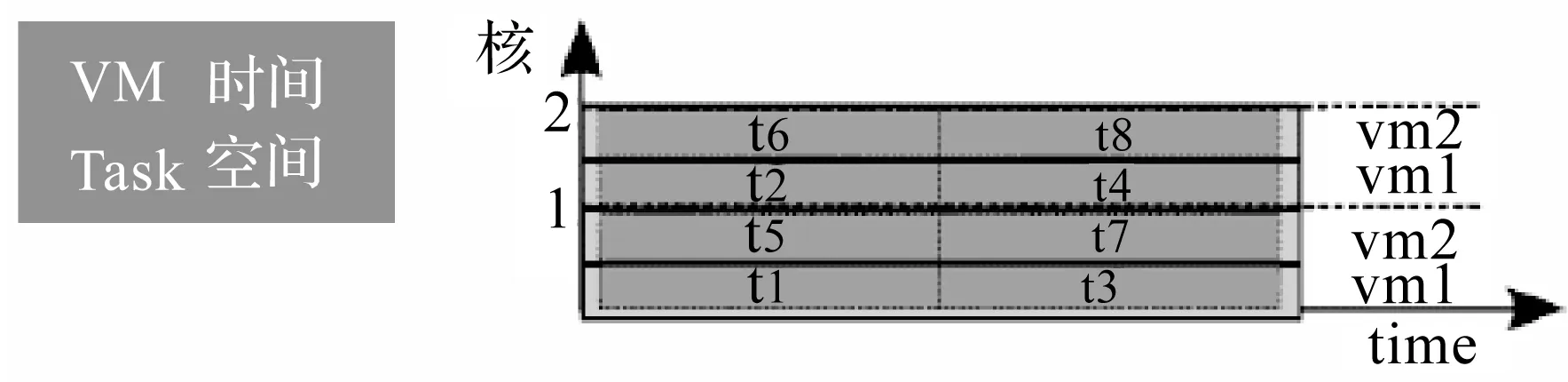
图5 处理器任务处理策略c

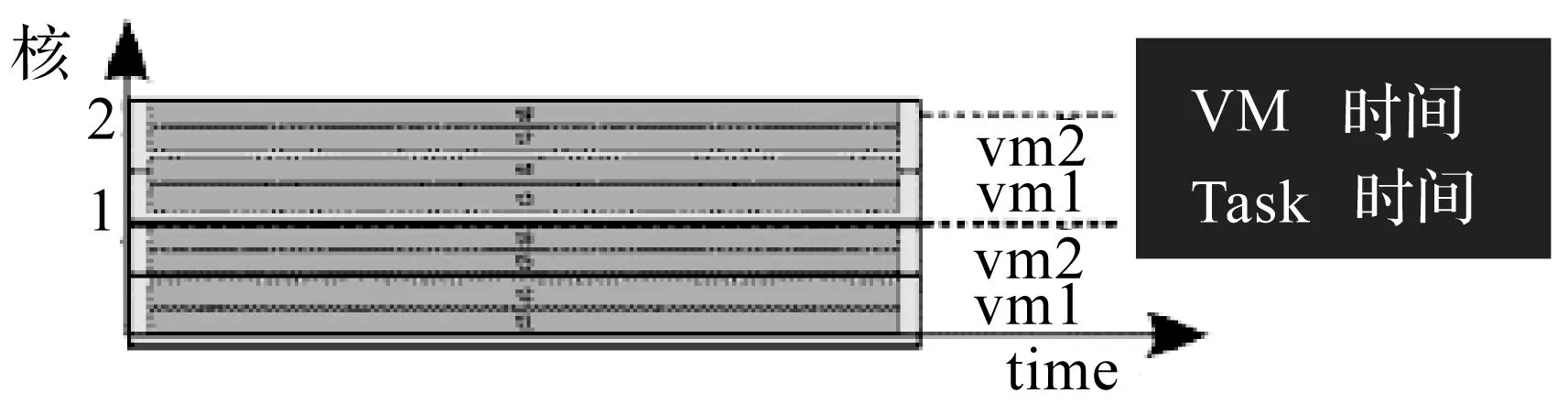
图6 处理器任务处理策略d

设虚拟机共接收到p个云任务(Cloudlet)，每个任务包含r(j)，j=1,2,…,p条执行指令，主机有n个处理单元，每个处理单元的处理长度是cap(i)，i=1,2,…,n，cores(j)表示任务需要的处理器个数，主机处理能力cp表示如下：

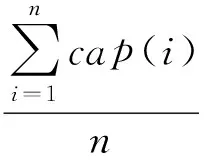
(14)

从而在虚拟机的空间共享模式下，虚拟机负责执行的任务j的执行耗费时间ET为：

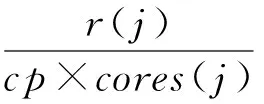
(15)

任务j的服务等待时间WT为：

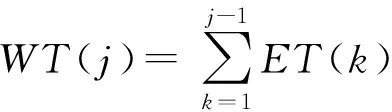
(16)

因此空间共享模式下任务j的完成时间表达如下：

FT(j)=WT(j)+ET(j)=

(17)

对于时间共享模式情况下多任务同时处理，因此任务j的服务等待时间为0，任务处理所需耗费的时间ET也表示为式(15)，只不过主机的处理能力cp计算方式有多不同：

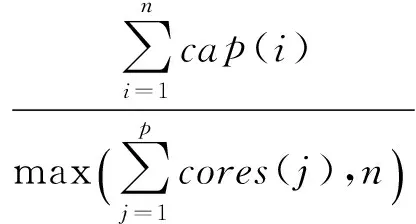
(18)

因此时间共享模式下任务j的完成时间表达如下：

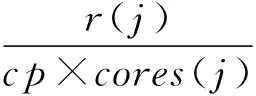
(19)

通过前面的对比可以看出，虚拟机的空间共享模式虽然会对用户服务造成等待感，但是一旦得到云端响应后，会很快处理完。而时间共享模式相对而言能够及时响应用户的请求，但是单个任务的处理时间会比较长。事实上，无论哪种模式下虚拟机真正用于响应和处理访问请求的时间都为ET，只是由于所分配到的资源不同，所耗时间有所不同而已。

2.3 基于网络拓扑的网络延迟时间

云计算架构在庞大的计算机网络之上，拥有众多的网络传输与通信设备，连接着全球各地的终端客户，从而网络拓扑结构成为云服务系统的服务基石。虽然网络信息传输的延迟直接影响着整个服务系统的服务质量，对云服务系统建设者、使用者和管理者而言，网络实际的物理拓扑结构并不是他们关心的对象，且也不是他们能够进行改造来减少网络延迟力所能及的内容[13]。因此多数情况下，网络延迟时间只是作为云服务网络的一个外生特性来使用，并在可能的情况下通过路由算法来缩短网络延迟。通常使用如下所示的延迟矩阵来表示网络各主要节点在信息传输时的延迟状况：

(20)

其中lij表示信息或数据从网络节点i到j的传递耗时，即在i节点传输指令下达后还需要延迟lij毫秒后才能将信息传达j节点，如图7所示。该矩阵表示了网络中r个主要实体之间的数据传输延迟信息，如亚、非、欧等世界主要区域，体现为区域入口端和出口端的速度。

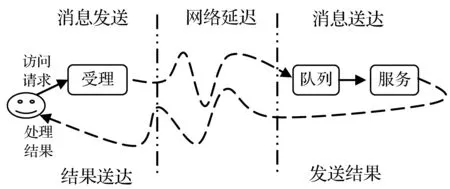
图7 网络传输延迟示意图

图7说明了云服务中网络拓扑造成的数据延迟现象，即网络拓扑的物理性质导致了云客户发送与接收信息的延迟，这部分延迟也应该直接计入云服务提供商的服务质量之中。

网络拓扑结构的描述通常采用BRITE格式将网络各节点信息全部包含进去。云环境中的节点包括主机、数据中心、云代理等。BRITE中节点信息包括节点编号，矩阵中的行号与列号，出、入度等信息，边信息包括边号、开始节点、结束节点、欧式距离、传递延时、带宽等信息。这些信息的纳入为网络各节点延时的计算提供了直接依据。

2.4 基于系统响应时间的云服务排队模型

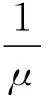
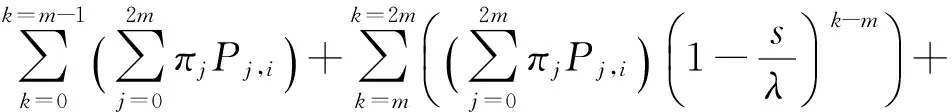
(21)

其中lij表示从客户端到云处理端的网络延时。可以看出系统响应时间主要有三部分组成：队列等待时间、服务处理时间和网络延迟。

3 结 语

关于这个云服务系统服务水平评估模型的数值仿真验证有两种方式：随机仿真法和推理仿真法。随机仿真法利用蒙特卡罗方法生成符合特定分布特征的随机数据，借此模仿服务系统的运行状况，最后将需要考察的服务系统状态变量所有实例值以均值、方差等统计变量的形式来描述。随机仿真能够很好地模拟现实中的哪种不确定性，并且能够检验系统在分布允许情况下的极端点表现，全方位进行服务检验。但是正是由于随机仿真所具有的随机性，每次仿真所产生的结果都不一样，只是在统计意义上无限趋近于状态变量理想值，导致取值误差。同时随机仿真必须在足够次数的仿真情况下才能得到具有说服力的数据，这就要求有足够的仿真次数，需要耗费大量的时间。

推理仿真法直接使用随机变量的统计特性来进行推理仿真，而不是去模拟随机变量的统计特性。这样的仿真直接采用推导出来的解析公式值进行仿真，得到的是状态变量的解析值，而不是统计值，消除了随机性误差，也极大地减轻了系统的运算工作量。但是由于统计特性在集中表现了绝大部分样本点信息的同时也会略掉个别极端点的信息，导致对系统的检验不完备，无法发现系统针对极端情况可能出现的问题。

由于云计算的仿真需要对大量的硬件资源和大量的用户访问进行仿真，计算量非常庞大，如果继续采用随机仿真的方法，进行实验的设备要求很高，时间花费难以想象。因此本文拟采用推理仿真法在后续的研究中对云服务系统进行分析，为此首先需要检验推理仿真法结果的有效性。

基于式(21)给出的系统响应时间解析值，通过将其与采用同样假设的随机仿真结果进行对比的方式来验证本服务系统评估模型的有效性。采用基于Petri网的Artifex仿真引擎进行云服务离散事件的仿真，在不同数目的虚拟机的情况下比较两个方针结果中的均值差异，结果如图8所示。

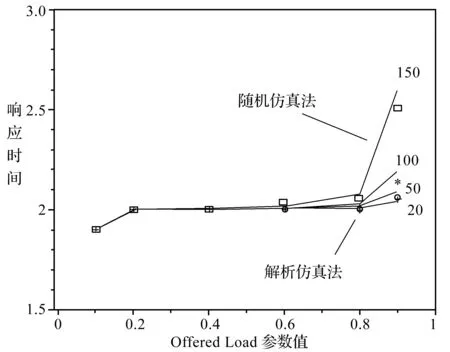
图8 仿真结果对比

图中折线代表的是采用随机仿真法在不同参数取值下的所有访问请求的系统响应时间的均值，符号点表示通过解析式仿真得到在马氏链的各观察点上系统的响应时间。四条线上对应的数字表示仿真的虚拟机的个数。从图中可以看出，两种方法得出的响应时间结果是非常接近的，除去随机仿真法的随机性误差，可以认为本文提出的云服务系统的评估模型是有效的，使用解析仿真的方法进行云服务系统的仿真也是可行、有效的。

[1] Du N H,Huang H L,Li L F. Can online trading survive bad-mouthing? An experimental investigation[J].Decision Support Systems,2013,56(6):419-426.

[2] Su Q,Chen L.A method for discovering clusters of e-commerce interest patterns using click-stream data[J].Electronic Commerce Research & Applications,2015,14(1):1-13.

[3] Su Q,Huang J J,Zhao X D.An information propagation model considering incomplete reading behavior in microblog[J].Physica A Statistical Mechanics & Its Applications,2015,419(2):55-63.

[4] Lin C H, Liu D, Pang W, et al.Sherlock:A Semi-automatic Framework for Quiz Generation Using a Hybrid Semantic Similarity Measure[J].Cognitive Computation,2015,7(6):667-679.

[5] Ghosh R, Longo F. Scalable Analytics for IaaS Cloud Availability[J].IEEE Transactions on Cloud Computing, 2014,2(1):57-70.

[6] 赵娉婷.云计算环境下服务信任度评估技术的研究[D].北京:北京交通大学,2014.

[7] Calheiros R N, Ranjan R, Beloglazov A,et al. CloudSim: a toolkit for modeling and simulation of cloud computing envi-ronments and evaluation of resources provisioning algorithms[J].Software: Practice & Experience, 2011,41(1):23-50.

[8] Gotelli N J, Wener U. Statistical challenges in null model analysis[J]. Oikos,2012,121(2):171-180.

[9] 马满福,王梅.云环境下基于服务等级协议的信任评估模型[J].计算机应用,2015,35(6):1567-1572.

[10] 车建华.虚拟计算系统性能和可用性评测方法研究[D].杭州:浙江大学,2010.

[11] Vani B, Priya R C M. A Survey on the Security Issues in Cloud Computing[J]. International Journal of P2P Network Trends and Technology, 2014(11):16-19.

[12] Jesús Montes, Alberto Sánchez, Bunjamin Memishi, et al.GMonE: A complete approach to cloud monitoring[J]. Future Generation Computer Systems, 2013,29(8):2026-2040.

[13] Chard K, Caton S, Rana O, et al. Social Clouds: A Retrospective[J]. IEEE Cloud Computing, 2015, 2(6):30-40.

CLOUDSERVICEQUALITYEVALUATIONMODELBASEDONSYSTEMRESPONSETIME

Yang Zhexi1Xue Huacheng2

1(CollegeofStandardization,ChinaJiliangUniversity,Hangzhou310018,Zhejiang,China)2(SchoolofManagement,FudanUniversity,Shanghai200433,China)

The response time is one of the key quality indexes of cloud service system, which means that the longer of system response time, the more of losing customers. Queuing waiting, server processing time and network delay constitute the overall response time of cloud service access, and the Markov chain of observation points is generated by embedded Markov chain. The random arrival of cloud access is simulated by the non-aftereffect property of Markov chain, and the queuing model of cloud service is constructed to evaluate the quality of cloud service. At the same time, the validity of the proposed cloud service quality evaluation model is verified by analytic simulation.

Cloud computing Response time Queuing theory Markov chain

TP393

A

10.3969/j.issn.1000-386x.2017.10.007

2016-12-14。浙江省科技计划重点项目(2016C25G2080022);杭州市哲学社会科学规划课题(2015JD30);浙江省教育厅项目(Y201432184)。杨喆曦，讲师，主研领域：均衡优化，信息化管理，标准化。薛华成，教授。