一种基于Stirling图枚举算法的分球入盒问题求解

彭哲也 谢民主

(湖南师范大学物理与信息科学学院 湖南 长沙 410081)

一种基于Stirling图枚举算法的分球入盒问题求解

彭哲也 谢民主*

(湖南师范大学物理与信息科学学院 湖南 长沙 410081)

已有的分球入盒问题解法通常只关注分球的总方案数，目前尚没有公开的计算机算法来枚举出所有具体的分球方案，而方案的枚举是生物信息学中一些分区优化算法的基础。受第二类Stirling数的递推公式的启发，提出一个新的数据结构——Stirling图。在此基础上设计一个算法来枚举p个不同球分配到q个相同盒子里的所有不同的方案。当p和q较大，枚举出所有的方案不可行时，设计另一个算法在整个方案空间实现均匀采样，输出指定个数的方案。测试结果表明，这些算法在内存为8 GB的普通PC上可在合理的时间内枚举出上百万组不同的方案。

分球入盒问题 第二类Stirling数 枚举算法 Stirling图 均匀采样

0 引 言

分球入盒是组合数学中的经典问题，在组合优化中有广泛的应用。把p个球放入q个盒子里，根据球和盒子是否相同可以分为四种不同的模型：(1) 球相同盒子相同；(2) 球相同盒子不同；(3) 球不同盒子不同；(4) 球不同盒子相同。每种模型又进一步分为盒子是否允许为空这两种情形。本文主要讨论球不同盒子相同的这类模型。

将p个有区别的球放入q个相同的盒子中，要求所有盒子都非空的方案数为第二类Stirling数，记作S(p,q)[1]。例如，将编号为A、B、C、D的4个小球放入2个相同的盒子里的所有不同放法可以表示如下(盒子用集合表示)：[{A},{B,C,D}]，[{B},{A,C,D}]，[{C},{A,B,D}]，[{D},{A,B,C}]，[{A,B},{C,D}]，[{A,C},{B,D}]，[{A,D},{B,C}]。因此S(4,2)=7。

第二类Stirling数在数论、组合论、代数拓扑、算法最优化等领域都有相关的应用[2]。显然，当pq且q>1时，第二类Stirling可由以下递归算法求解:考虑第p个球，该球不是独占一个盒子就是和其他球在同一个盒子中。第p个球独占一个盒子：其他p-1个球分配到其他q-1个非空盒子中的所有方案数为S(p-1,q-1)；第p个球不独占一个盒子的情况则是：其他p-1个球放入q个非空的盒子中，第p个球放入q个盒子的任意一个中，这样共有qS(p-1,q)种方法。这样就得到了第二类Stirling数的递推公式：

S(p,q)=S(p-1,q-1)+qS(p-1,q)

(1)

将p个有区别的球放入q个相同的盒子中, 当盒子允许为空时，令其不同的方法数为F(p,q)，显然：

F(p,q)=S(p,1)+S(p,2)+…+S(p,q)

(2)

第二类Stirling数的计算已经得到了广泛深入的研究[3]，但是目前尚没有公开的计算机算法来枚举出所有具体的分球方案。枚举是计算复杂性理论中的一类基本运算，是理论计算机科学中一个重要分支。自从1979 年 Valiant 首次提出枚举运算以来[6]，人们对枚举运算进行了大量的研究[7]，其中最典型的枚举方法有枚举问题实例的所有解或统计问题实例中解的个数[8]。

近年来，随着DNA测序的快速发展，利用多倍体基因组的DNA测序片段如何组装出构成多倍体的多个单体型[11]和利用环境群体微生物的深度DNA测序序列重构该群体的微生物基因组[12]等问题的研究成为生物信息学的研究热点。这些问题的数学建模通常是把DNA测序序列分配到多个分区中以满足特定的优化目标。因此，分球入盒方案的枚举成为一些求解这类问题优化算法的基本操作[11]。

本文受第二类Stirling数的递推公式的启发提出了一个新的数据结构——Stirling图。在此基础上设计一个算法来枚举p个不同球分配到q个相同盒子里的所有不同的方案；当p和q较大时，不可能枚举出所有的方案，该算法则在整个方案空间实现均匀采样，输出指定个数的方案。在内存为8 GB、主频为2.5 GHz的普通PC上的测试结果表明，该算法可以在几秒内枚举出上百万组的不同的方案。

1 Stirling图

本文用一个划分函数(Partition function)P(i)：{1,…,p}→{1,…,q}来表示p个不同的球分配到q个盒子中的一个具体方案。例如P(i)|i=1,2,3=1表示将编号为1，2，3的球放入第一个盒子里,P(4)=2表示将编号为4的球放入第二个盒子里。为了简便，下面用P(1..k)=1表示P(i)|i=1,…,k=1;P(1..k)=1..k表示P(i)|i=1,…,k=i。令p个不同的球分配到q个非空的相同盒子中的所有不同的方案的集合为S(p,q)，集合S(p,q)中不同方案的个数|S(p,q)|=S(p,q)。

当p0时，S(p,q)=1，即S(p,q)中只有一种分配方案，不同的球放到不同的盒子里，给球i所在盒子贴上标签i，则这种分配方案用P(1..p) = 1..p表示；当p>q=1，这时S(p,q)中同样只存在一种分配方案，即所有的球放在唯一的盒子中，给该盒子贴上标签1，则这种分配方案用P(1..p) = 1来表示；当p>q>1时，所有不同分配方案的集合S(p,q)可以用式(1)的证明过程构造出来：

S(p,q) ={P(p)=q·S(p-1,q-1)}∪

{S(p-1,q)·(P(p)=1…q)}

(3)

其中{(P(p)=q)·S(p-1,q-1)}表示将球p单独放到一个盒子中，且把该盒子贴上标签q(用P(p)=q表示)，然后把其他p-1个球分配到其他q-1个相同非空的盒子中(用S(p-1,q-1)表示)的所有不同方案的集合；而{(P(p)=1..q)·S(p-1,q-1)}则表示将前p-1个球分配到q个相同的非空盒子中(用S(p-1,q)表示，每个盒子由此过程获得了不同的标签)。然后将第p个球放到标签为i(i=1,…,q)的盒子中(用P(p)=1..q表示)的所有不同方案的集合。为了使用式(3)构造出分配方案的集合S(p,q)，本文引入如图1所示的Stirling图。

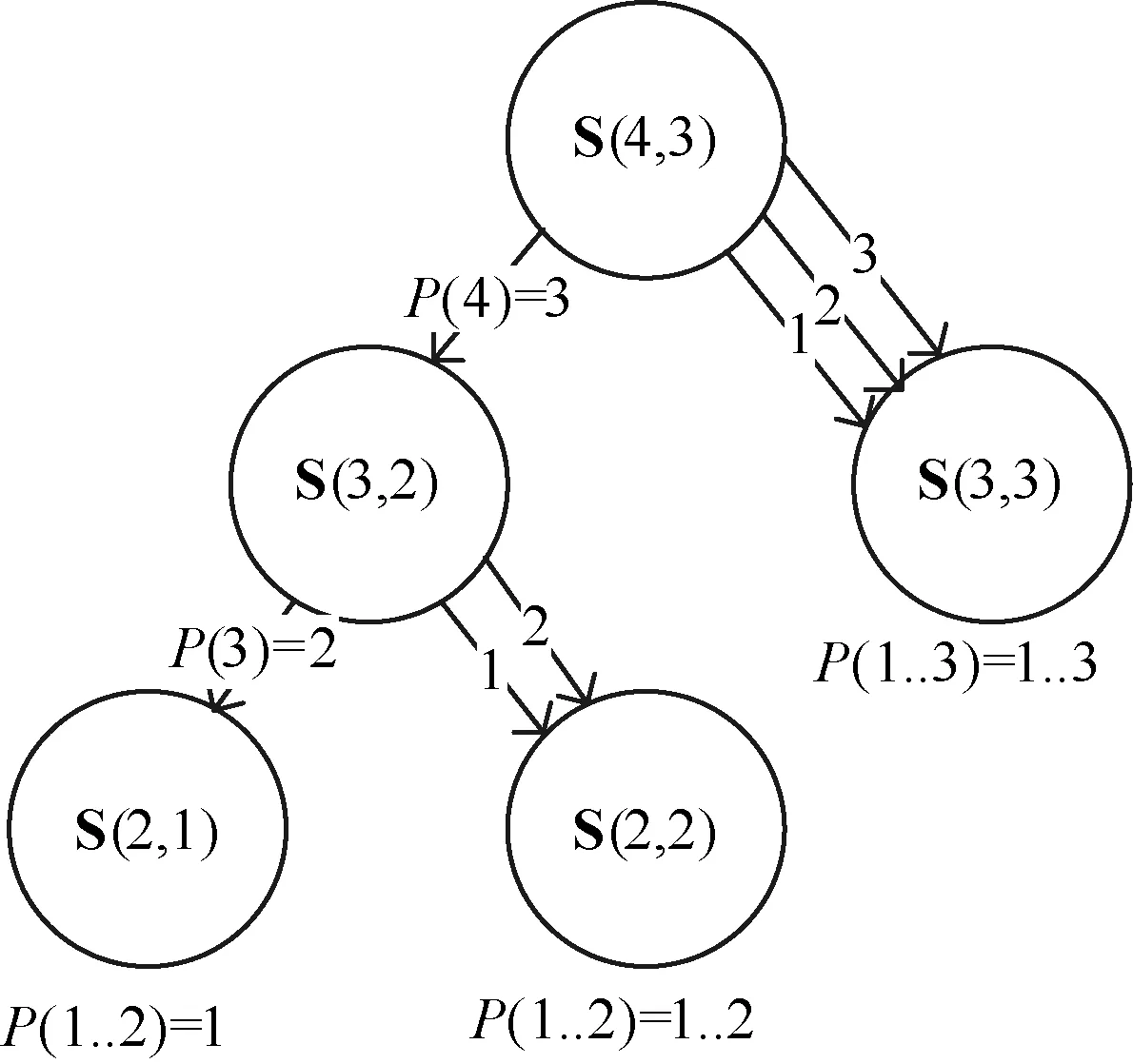
图1 Stirling图

Stirling图是一个有向无环图，其结点用S(j,k)来标记(j≥k≥1)。Stirling图的结点分为两类，一类是终端结点S(k,k)和S(j,1)，一类是非终端结点S(j,k)(j>k>1)。非终端结点S(j,k)结点有左右两个孩子结点，其左孩子结点为S(j-1,k-1)，右孩子结点为S(j-1,k)。图中用一条标签为P(j)=k的有向边由非终端结点S(j,k)指向其左孩子结点，用标签分别为P(j)=1,P(j)=2,…,P(j)=k的k条有向边指向其右孩子结点。对于两个结点S和S′，如果存在一条路径从S到S′，则S为S′的先驱结点，S′为S的后继结点。

在Stirling图中从非终端结点S(j,k)到其后继终端结点的一条路径代表把p个不同的球分配到q个非空的相同盒子的一种分配方案。如从S(3,2)到S(2,1)的路径代表一个分配方案：P(1..2)=1,P(3)=2;即把前两个球放到一个盒子里，第三个球放到单独的盒子了。由式(2)可知，从非终端结点S(j,k)到其所有后继终端结点的路径就代表把j个不同的球分配到k个非空相同盒子的所有不同分配方案。

对Stirling图，本文定义如下操作：

1)initiate(p,q):构造出一个Stirling图，包含结点S(p,q)及其所有后继结点，及相应的有向边。

2)destroy():删除Stirling图，释放内存。

3)count(j,k): 计算出S(j,k)，即|S(p,q)|。

4)pathTransverse(j,k):对Stirling图遍历从结点S(j,k)开始以任意终端节点结束的所有路径，即枚举出集合S(j,k)中的所有方案。

5)randomSample(j,k,n): 从集合S(p,q)中按照均匀分布随机选择n个不同的方案输出。

2 数据结构及算法实现

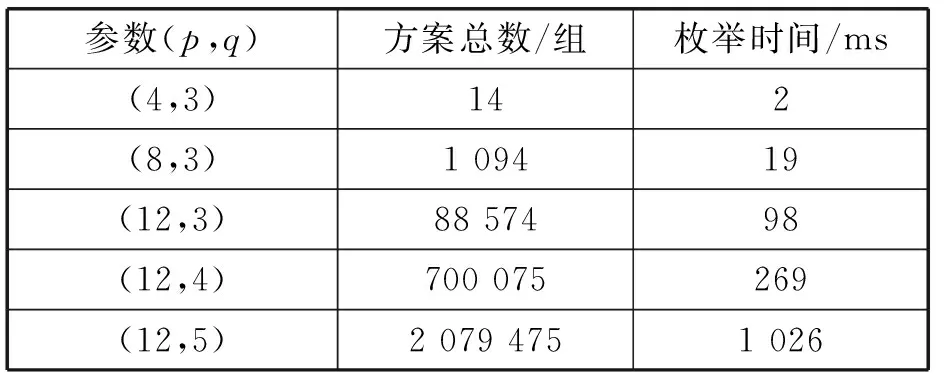
本文用一个(p+1)×(q+1)的二维数组M(假设下标是从0开始)来存储Stirling图的结点S(j,k):0

为了支持pathTransverse和count操作，元素Mj,k包含两个整型变量index和count，其中count用来记录S(j,k)的值，初始化为-1；index的取值范围为0到k，0表示进行pathTransverse操作时，下次访问的边是指向左孩子的边，index=i(1≤i≤k)表示下次访问的边是第i条指向其右孩子的边。

相关操作实现的伪代码如下所示:

structnode{

int index = 0;

int count = -1;

}

node[][] M;

void initiate(p, q){M = new node[p+1][q+1];}

void destroy() { delete[] M;}

intcount(int j, int k) {

if (M[j][k].count > 0)

//已经计算过，返回计算值

returnM[j][k].count;

if (j = k || k = 1) {

//终端结点

M[j][k].count = 1; return 1; }

M[j][k].count=count(j-1,k-1)+k*count(j-1,k);

returnM[j][k].count; }

voidpathTransverse(int j,int k){

// P记录球分配方案，第i个球分配到标签为P[i]的盒

//子中

int[] P = new int[j+1];

output_pathes (j, k, P, j); }

voidoutput_pathes (int j, int k, int[] P, int balls){

if (j = k) {

//终端结点，输出P(1..k) = 1..k

for(i= 1 .. k) { P[i] = i; }

输出分配方案P[1], …, P[balls];

return; }

if (k = 1) {

//终端结点，输出P(1..k) = 1

for(i= 1 .. j) { P[i] = 1; }

输出分配方案P[1], …, P[balls];

return; }

if (M[j][k].index = 0) {

P[j] = k;

//访问指向左孩子的边

M[j][k].index++;

output_pathes(j-1, k-1, P, balls); }

//访问左孩子

while(M[j][k].index ≤ k) {

//访问指向右孩子的边

P[j] = M[j][k].index; M[j][k].index++;

output_pathes(j-1, k, P, balls); }

//访问右孩子

M[j][k].index=0;

//恢复初始值

}

void randomSample(int j, int k, int n){

//n必须小于count(j, k)

int[] P = new int[j+1];

sample_pathes(j, k, P, j, n);

}

voidsample_pathes(intj, intk, int[] P, int b, int n){

if(n< 1){ return; }

if (j = k) {

//终端结点，输出P(1..k) = 1..k

for(i = 1 .. k) { P[i] = i; }

输出分配方案P[1], …, P[b]; return; }

if (k = 1) {

//终端结点，输出P(1..k) = 1

for(i= 1 .. j) { P[i] = 1; }

输出分配方案P[1], …, P[b]; return; }

intn_left = n;

int[] n_a = new int[k+1];

//通过均匀分布随机采样，获得通过其指向左右孩子结

//点的

// k+1条有向边的采样个数

get_sample_number(j, k, n, n_a)

if (M[j][k].index = 0) { P[j] = k;

//访问指向左孩子的边

M[j][k].index++;

sample_pathes(j-1, k-1, P, b, n_a[0]); }

//访问左孩子

while(M[j][k].index < k) {

//访问指向右孩子的边

P[j] = M[j][k].index;

M[j][k].index++;

sample_pathes(j-1, k, P, b, n_a[P[j]]); }

//访问右孩子

M[j][k].index=0;

//恢复初始值

}

voidget_sample_number(intj, intk, intn,int[] n_a){

float r = n/count(j, k);

//采样率

令count(j-1, k-1)*r的整数部分为a1，小数部分为e1，count(j, k-1)*r的整数部分为a2，小数部分为e2；

n_a[0] = a1;

floatpl = e1/(e1+k*e2), pr = e2/(e1+k*e2);

for(i= 1.. k) {

n_a[i] = a2; }

intn_left = n - a1 - k*a2;

while(n_left> 0){

//得到一个在[0, 1]之间均匀分布的随机数rand

floatrand = random();

if(rand ≤ pl) {n_a[0]++; }

else { intind = (rand - pl)/pr +1; n_a[ind]++; }

n_left--;}

}

对于盒子允许为空的情况，利用Stirling图枚举出所有的分配方案和按照均匀分布随机采样n个不同的方案的算法也容易实现。在盒子允许为空的情况下，令p个不同的球分配到q个相同的盒子中的所有不同方案的集合为F(p,q)，显然有：

F(p,q)=S(p,q)∪S(p,2)∪…∪S(p,q)

(4)

枚举出F(p,q)的算法如下所示:

F(int p, int q){

for(i = 1…q) { pathTransverse(p, i); }

}

当需要按照均匀分布随机采样输出n个不同的方案时，可按照get_sample_number的思路把n按照S(p,1),S(p,2),…,S(p,q)集合的大小划分成n1,n2,…,nq，然后再依次调用randomSample(p,1,n1),randomSample(p,2,n2),…,randomSample(p,q,nq)即可。

3 实验结果

本文算法用Java编程实现，测试计算机内存为8 GB，CPU为Intel酷睿i5 3210M 2.5 GHz的PC机。图2-图4分别表示的是F(3,2)、F(4,2)、F(4,3)在控制台输出的枚举结果。

图2 F(3,2)枚举结果

图3 F(4,2)枚举结果

图4 F(4,3)枚举结果

由于目前没有类似的算法可以横向比较，我们通过几个用例来测试本文算法的性能。如表1所示，当p和q增大时，F(p,q)枚举出所有分配方案所需的时间基本上与方案总数成线性增长；当p=12,q=5时，F(p,q)可以在约1秒钟的时间内枚举出2百余万种不同的方案。

表1 F(p,q)枚举时间

当方案总数过大，枚举所有的方案不可行时，我们在整个空间进行按照均匀分布随机采样100万个不同的方案进行输出，表2显示对于不同的(p,q)，随机采样算法randomSample(p,q,1 000 000)的运行时间。

表2 randomSample(p,q,1 000 000)运行时间

4 结 语

本文提出一种新的数据结构Stirling图，实现了该数据结构的操作算法，能枚举出不同的球分配到相同盒子中的所有不同方案。当方案总数过多无法枚举时，本文实现了随机采样操作算法，该算法按照均匀分布随机采样输出指定个数的不同的分配方案。测试结果表明，这些算法能有效解决球不同盒子相同的“分球入盒”方案枚举问题和均匀采样问题。实际应用中有很多优化问题如多倍体单体型组装[11]、宏基因组组装[12]等均可转化为“分球入盒”问题求解。本文提出的算法可以为这些问题的求解提供有效的分球入盒方案枚举基本操作的支持。

[1] Wikipedia. Stirling numbers of the second kind[EB/OL].(2016-12-7)[2016-12-14].https://en.wikipedia.org/wiki/Stirling_numbers_of_the_second_kind.

[2] 王娟. 第二类Stirling数及其推广[D]. 大连理工大学,2009.

[3] Abramowitz M, Stegun I A. Handbook of mathematical functions with formulas, graphs, and mathematical tables (9th printing)[M]. New York: Dover, 1972:824-825.

[4] Boyadzhiev K N. Close Encounters with the Stirling Numbers of the Second Kind[J]. Mathematics Magazine,2012, 85(4):252-266.

[5] Bleick W W. Asymptotics of Stirling Numbers of the Second Kind[J]. Proceedings of the American Mathematical Society,1974,42(2):575-580.

[6] Valiant L.The complexity of enumeration and reliability problems[J].SIAM Journal on Computing, 1979,8(3):410-421.

[7] Flum J, Grohe M .The parameterized complexity of counting problems[J]. SIAM Journal on Computing, 2004,33(4):892-922.

[8] 刘运龙, 王建新. 3-维匹配问题的一种固定参数枚举算法[J].计算机科学,2010,37(5):210-213.

[9] 谢民主, 罗锋, 唐烽. 单体型组装最大片段割参数化精确算法[J].小型微型计算机系统,2014,35(2):353-357.

[10] 张景云. 改进的堆的枚举算法的研究[J]. 计算机应用与软件,2012,29(7):264-265,273.

[11] Xie Minzhu,Wu Qiong,Wang Jianxin, et al. H-PoP and H-PoPG: heuristic partitioning algorithms for single indivi-dual haplotyping of polyploids[J/OL]. Bioinformatics. [2016-08-16] Doi: 10.1093/bioinformatics/btw537.

[12] Rose R, Constantinides B, Tapinos A, et al. Challenges in the analysis of viral metagenomes[J/OL].Virus Evolution.[2016-08-03].DOI:http://dx.doi.org/10.1093/ve/vew022.

RESEARCHONDISTRIBUTINGBALLSINTOBOXESENUMERATIONALGORITHM

Peng Zheye Xie Minzhu*

(CollegeofPhysicsandInformationScience,HunanNormalUniversity,Changsha410081,Hunan,China)

The existing researches on the problem of distributing balls into boxes usually focus on the total number of different ways to distribute balls into boxes, but there are no public computer algorithms to enumerate them. However, enumerating them is the foundation to design some partition optimal algorithms in Bioinformatics. Inspired by the recursive formula of the Stirling numbers of the second kind, the paper proposes a new data structure—Stirling diagram, and based on the data structure, designs an algorithm to enumerate all different ways to distribute p different balls into q same boxes. When p and q are larger and none of the schemes is feasible, we design another algorithm to achieve uniform sampling of a given number of different ways. Test results show that these algorithms can enumerate millions of different distributing ways in a reasonable period of time on a PC with 8 GB memory.

Distributing balls into boxes problem Stirling numbers of the second kind Enumerating algorithm Stirling diagram Uniform sampling

TP306.1

A

10.3969/j.issn.1000-386x.2017.10.044

2016-12-15。国家自然科学基金项目(61370172)。彭哲也，硕士生，主研领域：生物信息学。谢民主，教授。