基于人耳听觉特性的房间冲激响应多点均衡
房倩倩,姚鼎鼎,李军锋,夏日升
基于人耳听觉特性的房间冲激响应多点均衡
房倩倩,姚鼎鼎,李军锋,夏日升
(中国科学院声学研究所,北京100190)
在以扬声器-房间系统为代表的音频重放系统中,整个房间的声学特性会受到扬声器的系统响应、房间反射等影响而产生失真。房间冲激响应的失真会影响声音信号的音质,进而降低听者的听音感受,因此必须对房间冲激响应进行均衡。考虑到人耳听觉具有主观性和单点均衡存在的均衡有效区域局限性等问题,提出了基于人耳听觉特性的房间冲激响应多点均衡算法。通过在传统均衡滤波器设计中加入适当响度滤波器,使代价函数由声压转变为响度,实现均衡结果由数学最佳转为听觉最佳。利用在不同位置的房间冲激响应数据进行均衡滤波器的设计,实现从单点均衡到多点均衡的优化,扩大均衡有效区域。
人耳听觉特性;房间冲激响应系统均衡;最小均方误差
0 引言
随着三维音频及虚拟环绕声等音频技术的发展,为了进一步改善听音感受,人们对音频系统的性能要求也在不断提高,房间冲激响应(扬声器-房间系统响应)均衡已经成为国内外研究的热点[1-3]。衡量音频系统品质的一个客观标准是其幅频特性的平坦性,由于房间反射、组件品质等因素的影响,普通音频系统的幅频响应平坦特性难以得到保证,因此需要对音频系统进行均衡处理。最常见的音频重放系统是扬声器-房间系统,它的声学特性会受到扬声器的系统响应、房间反射等影响,是音频系统均衡研究的重点和难点。运用数字均衡滤波器技术实现房间冲激响应的补偿与优化,可以消除房间声学特性对音频信号的影响,对声音进行修正,改善聆听感受,获得更加真实的声重放效果,使听者有不一样的听音感受。所谓均衡是指在信号传输过程中,为了减少传输信号的线性失真,针对信道传递函数偏离其理想现状而进行的补偿过程。20世纪80年代中期,Mourjopoulos J等人提出了采用数字滤波器改善房间声学特性的方法,并且采用了有限冲激响应(Finite Impulse Response,FIR)滤波器均衡技术[1]。FIR滤波器具有容易设计、稳定和线性相位等优点,但是为了达到较好的均衡效果,FIR滤波器的阶数往往较高。Greenfield R等人相继提出了无限冲激响应(Infinite Impulse Response,IIR)结构的均衡滤波器[2-3],指出IIR滤波器的阶数比FIR滤波器的阶数要少,但是IIR滤波器不具有线性相位,并且需要考虑系统的稳定性。由于人耳对低频段声音的分辨率更高,因此需要重点对低频段进行均衡。文献[4-5]提出弯折频率滤波器方法,将线性频率转换成弯折频率域,在弯折频率域进行滤波器设计,可以着重优化低频段的频率响应,以更加接近人耳的听觉效应。但是在弯折滤波均衡方法中只有一个弯折系数可以控制频率的非线性分辨率,弯折效果不灵活,Kautz滤波均衡器应运而生[6-8]。Kautz滤波器是弯折滤波器的延伸,它可以实现更复杂的频率分辨率映射,缺点是求取理想极点与均衡滤波器系数过于复杂。除此之外,还有双二阶IIR滤波器级联结构对房间响应进行均衡的算法[9-13]与定极点并联均衡滤波器的设计算法[14-17]。传统房间冲激响应均衡方法都是以声音信号的幅值为度量标准的,但是人耳听觉系统是非常复杂的,涉及到声学、语音学和听力学,并且与频率、声强等诸多因素相关。另外,人耳听觉系统对声音的感受具有主观性,声压大小与人耳对声音强弱的感觉并不完全一致,甚至存在声压降低但人耳感觉更响的情况,这是因为人对声音的感受不仅与声压大小有关,还与声音的频率成分有关。基于人耳听觉系统的复杂性与响度的物理特性,本文主要介绍以响度为度量的房间冲激响应多点均衡算法。通过在传统均衡滤波器设计中加入适当响度滤波器,使代价函数由声压转变为响度,实现均衡结果由数学最佳转为听觉最佳。
1 预处理
在实施房间冲激响应多点均衡处理前,首先需要进行房间冲激响应测量、房间冲激响应平滑、房间冲激响应建模预处理。房间冲激响应测量是为了得到各点理想的房间传输函数,房间冲激响应平滑是为了减小均衡结果受时间、位置变化的影响,房间冲激响应建模是通过多点房间冲激响应数据建立能代表整个房间声学特性的模型,使单点均衡转化为多点均衡。
1.1 房间冲激响应测量
理想的房间冲激响应的测量结果是房间冲激响应均衡的基础和前提。房间冲激响应测量工作的整体思路是:选择合适的源信号作为激励输送给整个房间系统,通过传声器记录输出信号,对输入信号和输出信号进行解相关运算求得房间传输函数。在整个测量工作中最重要的就是选择理想的源信号。本文利用最大长度序列(Maimum Length Sequence,MLS)信号进行房间冲激响应测量。在房间的一个区域内选择五个点进行各点的房间响应测量(见图1),得到五个点的房间冲激函数。

图1 测量点位置图
1.2 房间冲激响应平滑
利用在房间内多点测量得到的房间传输函数进行均衡器设计的过程中,考虑人耳听觉特性和实践经验,对测量得到的数据进行频率响应平滑。房间冲激响应会随着时间和位置发生很大变化,为了得到理想的均衡效果,选择适当的均衡滤波器长度和预先对房间冲激响应进行平滑,是解决均衡效果受位置影响问题的重要途径。考虑到人耳听觉系统对声音频率的分辨率不是线性的,本文采用1/3倍频程的复数平滑(也称为频率响应平滑)方法进行房间冲激响应的平滑。
1.3 房间冲激响应建模

2 基于人耳听觉特性的房间冲激响应均衡
在传统的房间冲激响应均衡过程中,常采用自适应算法求取最佳的均衡滤波器系数,如图3所示()为测量房间传输函数时所采用的输入信号,其一般选用MLS信号;()为对房间各点测量后得到的房间冲激响应模型,应使其尽量能反映整个房间的声学特性;()为所要设计的均衡滤波器;()为经过房间传输和均衡滤波器处理后的输出信号;期望信号T()为加入适量延时的输入信号,即理想的均衡效果是输出信号无限逼近输入信号;()为期望信号与输出信号之间的误差,利用LMS算法不断调整均衡滤波器系数使误差减小,由此可求得均衡滤波器的最佳系数。

图2 房间冲激响应建模结果

图3 传统房间冲激响应均衡算法
在上述算法中,对不同的频率是等同处理的,所得结果在整个频率范围的总体误差最小,这样在数学上是最佳的,从听觉上未必如此。为了得到听觉上最佳的均衡效果,可以在计算误差时对不同的频率进行加权处理。在听觉系统分辨率较高的频率范围,应加大其对误差的贡献。相反,在听觉系统分辨率较低的频段上允许其误差较大,可减少其对总体误差的贡献。由于响度是表征人耳听觉系统对声音的主观物理量,通过研究声压与响度的关系,设计响度转换滤波器(),如图4所示,对误差信号()进行加权处理,使其转换为响度误差1()。这样在房间冲激响应均衡过程中,控制目标由声压变为响度,得到的均衡结果更贴近听觉最佳。
整个均衡过程分为三部分:
(1) 通过测量、平滑、建模得到房间冲激响应模型();
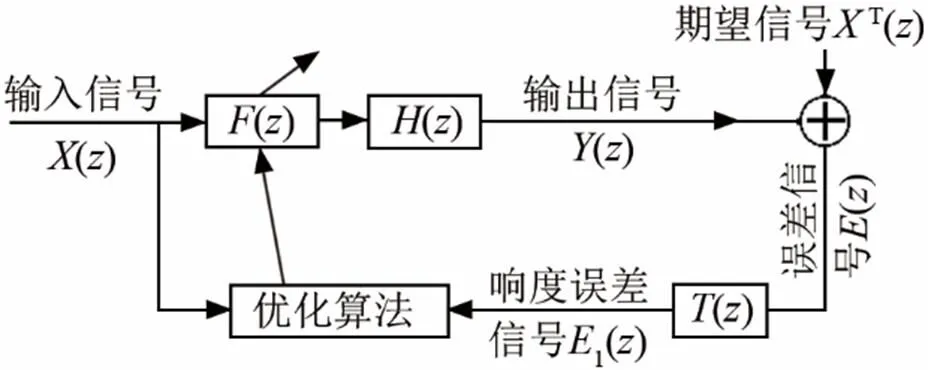
图4 基于响度度量的房间冲激响应均衡算法
(2) 设计响度转换滤波器,将误差信号由声压转化为响度;
(3) 利用LMS算法求取均衡滤波器系数,对()进行均衡。
2.1 设计响度转换滤波器
如图5[18]所示,等响曲线有很多条,但对任意一条等响曲线而言,共同点是:不同频率声音的声压级是不同的,而且整体趋势一致。从图5可以看出,随着频率的增大,声压级变化引起的响度变化关系并不是线性的。举例来说,在频率为1 kHz时,声压级10 dB的差异只能引起响度级约为10 phon的变化,而在频率为100 Hz时,声压级10 dB的差距却能引起响度级约为20 phon的变化。响度是反映人耳对声音大小的感受的主观物理量,对于不同的频率上的声压级差异,人耳的主观感受也是不同的。为了将声压刻度的差异转化为响度刻度的差异,必须要研究不同频率上声压级变化引起的响度变化的关系,然后利用此关系设计响度转换滤波器,以响度为度量设计均衡滤波器。
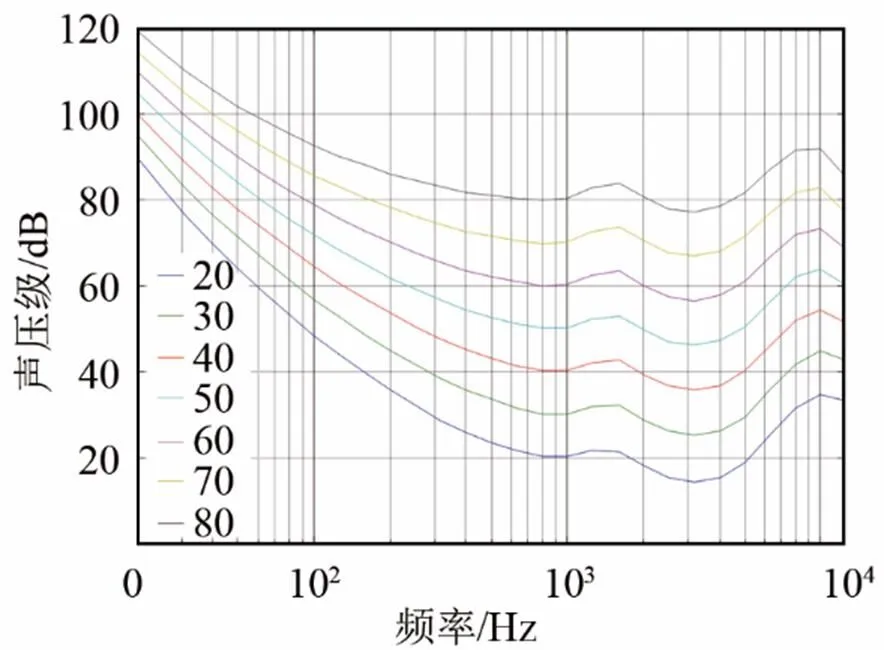
图5 等响曲线[18]
选择20 phon和80 phon的两条等响曲线为研究对象,观察在不同频率下,响度级从20 phon升至80 phon需要声压级做出多少改变。如图6所示,同样是发生60 phon的响度级变化,不同频率所需的声压级是不同的,这个关系可以视为物理的声压误差与人耳主观的响度误差的对应关系,类似于声压级误差经过一个滤波器放大或缩小了的该误差对人耳主观听觉的影响。引起同样的响度级变化,需要比较小声压级变化的频段是人耳比较敏感的频段,即人耳可以轻易捕捉到这个频段的声压级变化;需要比较大声压级变化的频段是人耳不太敏感的频段,即人耳在这个频段可以容忍较大的声压级变化而听起来差不多。可以根据这个关系进行响度转换滤波器的设计。
设计响度转换滤波器,是为了将声压误差转化为更符合人耳听觉特性的响度误差,根据图6进行其分析,我们可以得到声压级变化与响度级变化之间的关系。设想将响度转换滤波器的幅频特性设计成图6曲线的倒置型,即需要使较小的声压级变化就能引起较大响度级变化的频段(人耳较为敏感的频段)有一个较大的增益,加大该频段的响度误差权重来逼近人耳特性;需要较大的声压级变化就能引起较大响度级变化的频段(人耳不太敏感的频段)有一个较小的增益,也就是允许该频段有较大的误差。得到的响度转换滤波器幅频特性如图7所示。
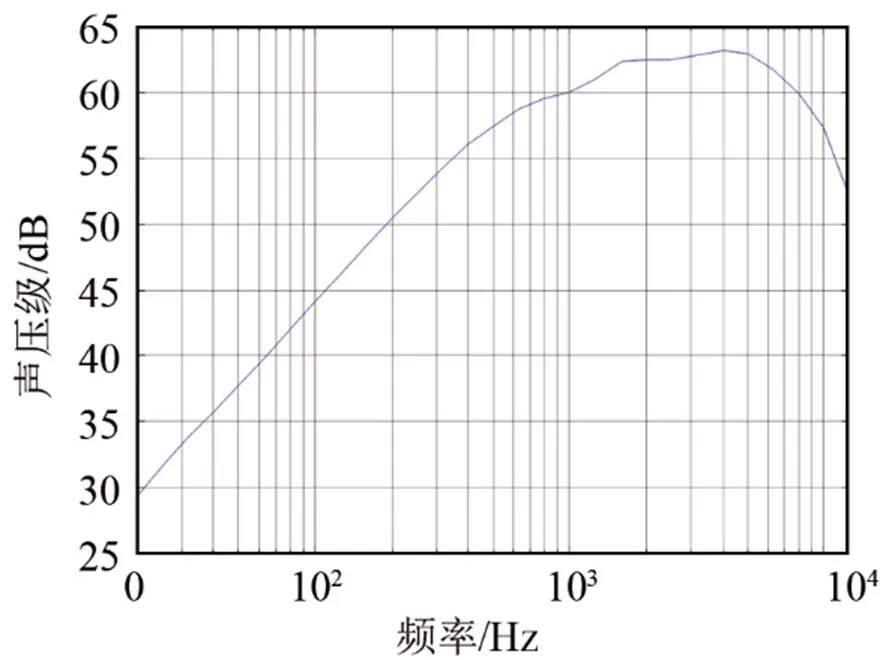
图6 不同频率响度级改变60 phon所需的声压级变化

图7 响度转换滤波器设计结果
2.2 均衡结果分析
利用LMS算法求得的均衡器系数对房间冲激响应模型及每个点的房间冲激响应进行均衡处理,图8中黑色曲线为房间冲激响应模型的幅频特性,蓝色曲线为均衡滤波器幅频特性,红色曲线为均衡后的房间冲激响应模型幅频特性。由图8可见,该方法取得了理想的均衡结果,即便是在低频段均衡结果较差,也将幅频特性的波动均衡至人耳不能察觉的范围之内。在得到理想均衡滤波器系数后,分别对测量到的三组音频系统相应进行均衡,分析均衡结果并与FIR滤波器、IIR滤波器,弯折滤波器(Warped IIR,WIIR)、Kautz滤波器的均衡效果进行比较,验证论文提出均衡方法的有效性和优越性。
图9给出了多种均衡方法的均衡结果。对比IIR均衡滤波器、FIR均衡滤波器、Kautz均衡滤波器,本文提出的均衡算法有一定优势,尤其是在低频段,均衡结果优于其他三种方法。而针对WIIR均衡滤波器,本文提出的方法在低频段的均衡结果虽然有所逊色,但是WIIR均衡滤波器在高频段的均衡结果却不及本文方法,这也验证了弯折均衡滤波器是牺牲高频段均衡结果来改善低频段均衡结果的结论。

图8 房间冲激响应的均衡结果

图9 不同方法的均衡结果比较
为了进一步对各类方法的均衡结果进行比较,本文引入两种幅度均衡误差评价标准,一种是传统线性均衡误差,另一种是加权误差。分别表示为

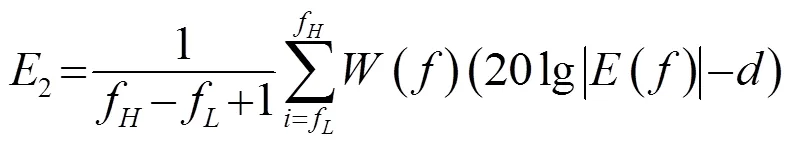

五种方法的均衡误差汇总,如表1所示。

表1 五种方法的均衡结果比较
计算得到的误差结果与图9分析结果一致,本文方法得到的均衡后的频谱基本平坦,计算得到的线性误差和加权误差分别为0.2917dB和0.8861 dB,幅频特性的峰谷起伏在±1.5 dB左右,大多数人的听觉系统对这种程度的起伏是无法察觉的。无论是线性误差还是加权误差,本文方法都优于IIR均衡滤波器、FIR均衡滤波器、Kautz均衡滤波器。对于线性误差,本文提出的方法虽然不及WIIR均衡滤波器,但是,本文方法在提高低频段均衡效果的同时没有影响其他频段的均衡结果,因此,在加权误差方面有一定优势。
3 结论
为了得到听觉上效果更佳的均衡结果,本文给出了基于响度度量的均衡方法,关键是设计响度转换滤波器将误差从幅度转换为响度,力求从更符合人耳听觉特性的角度设计均衡滤波器和评价均衡结果。多个均衡方法比较后的结果表明,引入响度滤波器确实可以在一定程度上改善低频段的均衡效果,而且不影响高频的均衡结果。
[1] Mourjopoulos J, Clarkson P, Hammond J. A comparative study of least-squares and homomorphic techniques for the inversion of mixed phase signals[C]//Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP'82. IEEE, 1982, 7: 1858-1861.
[2] Greenfield R, Hawksford M J. Efficient filter design for loudspeaker equalization[J]. Journal of the Audio Engineering Society, 1991, 39(10): 739-751.
[3] Hawksford M J. MATLAB program for loudspeaker equalization and crossover design[J]. Journal of the Audio Engineering Society, 1999, 47(9): 706-719.
[4] Smith J O, Abel J S. The Bark bilinear transform[C]//Applications of Signal Processing to Audio and Acoustics, 1995., IEEE ASSP Workshop on. IEEE, 1995: 202-205.
[5] Smith J O, Abel J S. Bark and ERB bilinear transforms[J]. IEEE Transactions on Speech and Audio Processing, 1999, 7(6): 697- 708.
[6] Paatero T, Karjalainen M, Harma A. Modeling and equalization of audio systems using Kautz filters[C]//Acoustics, Speech, and Signal Processing, 2001. Proceedings.(ICASSP'01). 2001 IEEE International Conference on. IEEE, 2001, 5: 3313-3316.
[7] Karjalainen M, Paatero T. Equalization of audio systems using Kautz filters with log-like frequency resolution[C]//Audio Engineering Society Convention 120. Audio Engineering Society, 2006.
[8] Karjalainen M, Paatero T. Equalization of loudspeaker and room responses using Kautz filters: Direct least squares design[J]. EURASIP Journal on Applied Signal Processing, 2007(1): 1-13.
[9] Ramos G, Lopez J J. Direct Method with random optimization for parametric iir audio equalization-applications to one way and multiway systems[C]//Audio Engineering Society Convention 116. Audio Engineering Society, 2004.
[10] Ramos G, López J J, Lloret J. Direct method with random optimization for loudspeaker equalization using IIR parametric filters[C]//Acoustics, Speech, and Signal Processing, 2004. Proceedings.(ICASSP'04). IEEE International Conference on. IEEE, 2004, 4: iv-97-iv-100 vol. 4.
[11] Ramos G, Lopez J J. Subjective evaluation of an equalization method for loudspeakers based on random parametric optimization of iir filters[C]//Audio Engineering Society Convention 116. Audio Engineering Society, 2004.
[12] Lopez J, Ramos G. Low Order IIR parametric loudspeaker equalization, a psychoacoustic approach[C]//Audio Engineering Society Convention 118. Audio Engineering Society, 2005.
[13] Ramos G, Lopez J J. Filter design method for loudspeaker equalization based on IIR parametric filters[J]. Journal of the Audio Engineering Society, 2006, 54(12): 1162-1178.
[14] Bank B. Direct design of parallel second-order filters for instrument body modeling[C]//Proc. International Computer Music Conference (ICMC 2007), Copenhagen, Denmark. 2007: 458-465.
[15] Bank B. Perceptually motivated audio equalization using fixed- pole parallel second-order filters[J]. IEEE Signal Processing Letters, 2008, 15: 477-480.
[16] Bank B, Ramos G. Improved pole positioning for parallel filters based on spectral smoothing and multiband warping[J]. IEEE Signal Processing Letters, 2011, 18(5): 299-302.
[17] Bank B. Audio equalization with fixed-pole parallel filters: An efficient alternative to complex smoothing[C]//Audio Engineering Society Convention 128. Audio Engineering Society, 2010.
[18] ISO. 226: 2003: ‘Acoustics-Normal equal loudness-level contours’[J]. Costs, 2003, 33(6): 802-803.
Multiple-point equalization of room impulse response based on human perception characteristics
FANG Qian-qian, YAO Ding-ding, LI Jun-feng, XIA Ri-sheng
(Institute of Acoustics, Chinese Academy of Science, Beijing 100190, China)
In sound reproduction system such as loudspeaker-room system, the acoustics of the room will affect sound quality. As a result, equalization is essential for room impulse response. Considering the human perception characteristics and the limitation of single-point-equalization, this paper presents a new digital filtering approach to the multiple-points equalization of room impulse response, which realizes a good match with the psycho-acoustical frequency scale of human hearing. Adding loudness conversion filters to traditional equalizer and transforming the magnitude to loudness results in an optimum effect in auditory scale. Using multiple-points room response data to design the equalizer contributes to improving single-point-equalization and enlarging the effective equalized zone. Finally, the multiple-points equalization of room impulse responsebased on the human perception characteristics is realized. The experimental results show that the proposed method which is based on the human auditory characteristics can obtain ideal equalization results, especially in the frequency band where auditory system is sensitive to frequency.
human perception characteristics; equalization of room impulse response; least mean square (LMS)
TB551
A
1000-3630(2017)-02-0152-05
10.16300/j.cnki.1000-3630.2017.02.010
2016-05-15;
2016-07-19
国家863计划(2015AA016306)、国家973计划(2013CB329302)资助项目。
房倩倩(1990-), 女, 山东济南人, 硕士研究生, 研究方向为音频信号处理。
姚鼎鼎, E-mail: simon.ydd@gmail.com

