相控聚焦超声与圆孔交互作用的散射特性研究
周进节,郑阳,张宗健
相控聚焦超声与圆孔交互作用的散射特性研究
周进节1,郑阳2,张宗健2
(1. 中北大学机械与动力工程学院,山西太原030051;2. 中国特种设备检测研究院,国家质量监督检验检疫总局无损检测与评价重点实验室,北京100029)
相较于传统超声检测,相控阵技术的声束聚焦控制能力使得相控超声检测的分辨率、信噪比和灵敏度等性能得到有效提升。但针对相控超声与缺陷的交互作用认识不足,导致目前检测技术无法对缺陷进行准确定性和精确定量。为此,建立了一维线阵相控超声检测圆孔缺陷的有限元模型,重点研究相控聚焦波束与圆孔缺陷交互作用的声场散射特性。结果表明,圆孔散射L模态的能量主要集中于正反射区和正透射区,且在透射区的能量大于反射区的能量,而在与入射声束垂直的方向上能量极其微弱,几乎没有散射能量;散射L模态沿入射方向呈轴对称分布;对于不同直径的圆孔缺陷,直径越大,在相同方向上散射波的能量越大;对于相同直径的圆孔,聚焦波与平面波入射时,散射波的分布规律相同,但聚焦波散射的能量明显高于平面波入射时散射的能量。
相控;聚焦超声;圆孔;散射特性;散射矩阵
0 引言
相控阵超声以其便于声束控制、检测范围大、结果直观等特点成为超声无损检测领域极具应用前景的技术之一[1-3]。随着电子技术的迅猛发展,商用超声相控阵的硬件电路已能支持256阵元同时激励和接收[4]。近年来,许多学者致力于研究超声相控阵成像算法,旨在利用相控阵检测信号提高成像质量,代表性的算法有全聚焦算法[5]、逆波场外推算法[6]和波数空间算法[7]等。但这些成像算法将各种缺陷均简化为完美散射体,认为所有缺陷散射声场在各方向分布规律相同,从而导致目前算法成像结果中圆孔缺陷显示为一片扇形区间,无法成像出圆孔缺陷的实际形状,更不能对圆孔进行精确的定量分析。而实际上,缺陷并非完美散射体,缺陷的散射信息是随入射波种类、方向,以及缺陷形貌、尺寸变化的[8-10]。
超声相控阵是通过控制各通道延迟参数来实现聚焦检测的,为实现超声相控阵高分辨率成像以对缺陷进行准确定性、精确定量,研究了相控阵合成聚焦声束与缺陷交互作用规律。聚焦声束与缺陷的交互作用主要体现在交互作用后的散射场分布上,从而可通过研究缺陷散射场分布来研究聚焦声束与缺陷的交互作用。
1 仿真模型的建立
建立一维线性相控阵超声与孔缺陷交互作用的二维有限元模型,如图1所示,在待检试件表面设置多个等间距分布的压强载荷来模拟相控阵传感器激励产生超声波,线性相控阵阵元数为32个,单个阵元宽度为0.5 mm,阵元中心间距为0.6 mm。待检试件为钢材,材料参数为密度7.85×103 kg/m3、杨氏模量2.1×105 MPa、泊松比0.26,几何参数为长50 mm、宽40 mm。在研究圆孔缺陷的散射特性时,当试件待检区域较大时,会增加计算时间,但当待检区域较小时,边界回波可能与缺陷散射信号混叠,增大散射信息提取的难度。综合考虑上述因素,本文拟采用较小区域模型进行计算,并将模型外边沿设置为吸收边界,以极大程度地减小甚至消除边界反射回波[11]。吸收边界由25层0.2 mm宽的阻尼层构成,各阻尼层是在待检材料上增设瑞利阻尼系数项而形成的,且从内边界至外边界各层阻尼系数值逐层增加。为了获取到缺陷处的散射信号,以缺陷中心为圆心设置一个半径为10 mm的检测圆,并在其上等间隔设置32个监测点,通过提取监测点的信号获得散射信息。
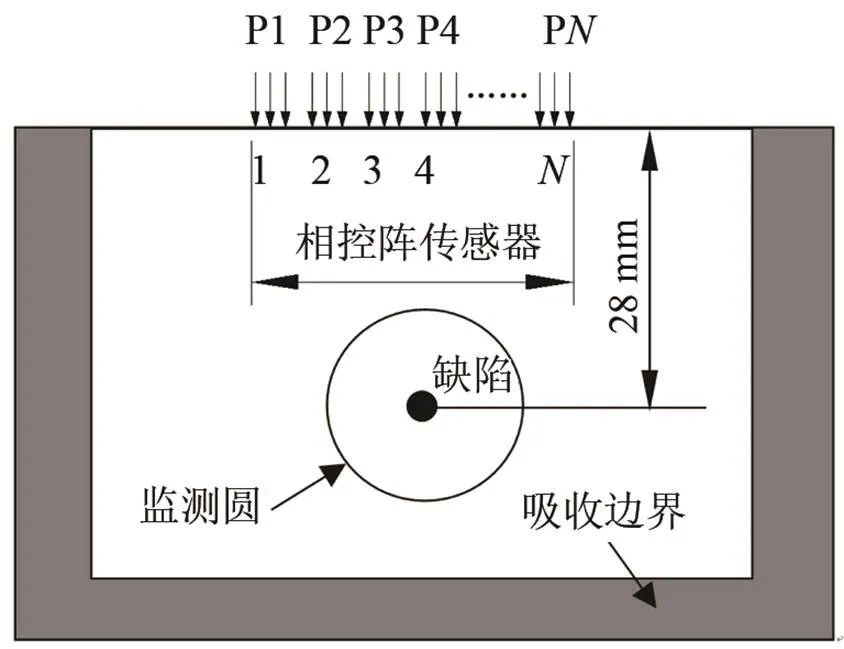
图1 相控阵超声与孔缺陷交互作用的二维有限元模型
2 相控超声与圆孔缺陷的交互作用
相控阵超声通过相位延迟可合成不同类型的声束,按合成超声波前可分为平面波束和聚焦波束。为此,在相控传感器的正下方设置圆孔缺陷,直径分别为0.5、1、1.5和2,对比研究相控阵超声平面波束和聚焦波束检测圆孔缺陷时的散射纵波分布规律,其中为超声纵波波长。
2.1 平面波束在圆孔缺陷处的散射特性
在有限元模型中,以相同延迟时间同时激励32个阵元,可合成平行于激励表面的平面纵波,简称平面波。研究平面波束在不同直径圆孔处的散射特性时,保持平面波从90°方向入射且激励能量不变。图2是相控超声平面波束与圆孔缺陷交互作用的仿真结果图。
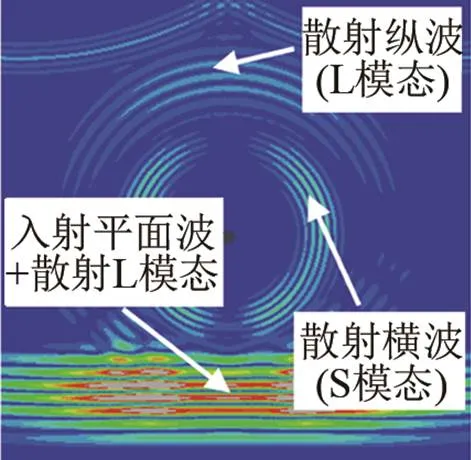
(a) 圆孔直径为0.5(b) 圆孔直径为

(c)圆孔直径为1.5(d)圆孔直径为2
图2 相控阵超声平面波与圆孔缺陷交互作用的仿真云图
Fig.2 Simulation images of phased array focused plane wave interacted with the hole defects of different diameters
如图2(a)所示,相控阵超声平面波在经过圆孔缺陷时,平面波与圆孔交互作用产生了两种不同模态的散射波,即散射纵波(L模态)和散射横波(S模态)。随着传播时间的推移,散射纵波和散射横波将会在时域上分开。从图2中可知,相控阵超声平面波束入射到圆孔缺陷时,在缺陷的反射区(正反射方向左右90°范围区域)存在散射纵波,并且随着圆孔直径增加,散射L模态的能量增加,在透射区(正透射方向左右90°范围区域)不能明显看出是否存在散射纵波。
2.1.1 周向散射系数
从信号监测圆上提取不同直径圆孔缺陷的周向散射信息,为了便于对比分析,对不同直径圆孔缺陷的周向散射系数进行归一化处理,并绘制圆孔缺陷散射L模态的周向散射系数图,如图3所示。
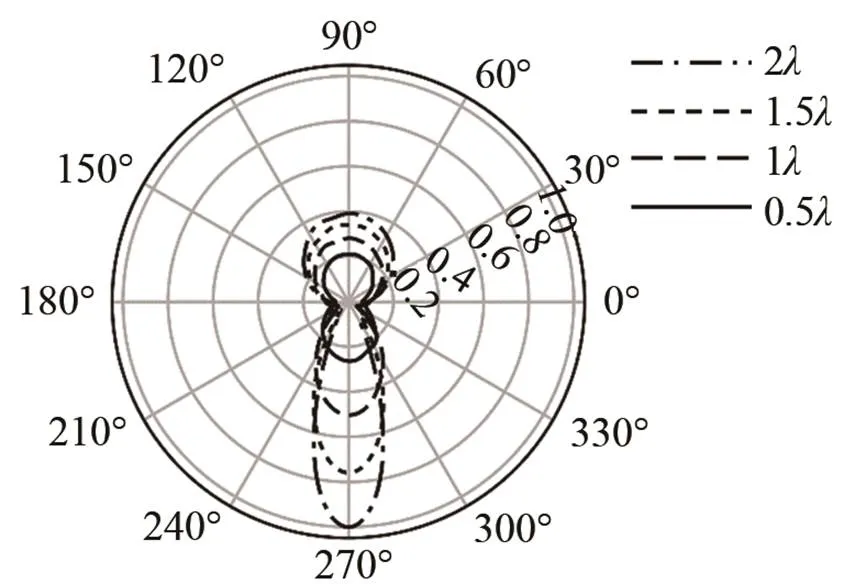
图3 平面波入射到圆孔缺陷的周向散射系数
从图3可知:(1)在反射区和透射区均存在散射纵波;(2) 散射L模态的能量随着圆孔直径增加而增加,且透射区的能量增幅大于反射区的能量增幅;(3)圆孔散射L模态的散射能量主要集中于90°及270°方向左右,且透射区的能量大于反射区的能量,而在与入射方向垂直的0°及180°方向上能量极其微弱,几乎没有散射能量;(4) 散射L模态关于入射方向呈轴对称分布。
2.1.2 全散射系数矩阵
全散射系数矩阵用于反映所有入射角下的散射场分布,对于圆孔缺陷可通过对称变换获取其他入射角下的周向散射系数,以此构成全散射系数矩阵。将各圆孔对应的全散射系数矩阵进行归一化处理,并分别绘制为散射矩阵图,如图4所示。
散射矩阵图中,横坐标为平面波的入射角度,纵坐标为散射角度,色彩值表示散射系数值。为了便于描述,引入以下特征词:“脊线”和“脊带”代表幅值明显高于相邻区域的线状区和带状区;“阱线”和“阱带”代表幅值明显低于周围区域的线状区和带状区。从图4可知:(1) 随着圆孔直径的增加,关于矩阵副对角线对称的脊带宽度逐渐变窄且能量变高;(2) 在副对角线上的脊带随着圆孔直径的增加在逐渐变宽,幅值能量逐渐增大,圆孔直径增加到2时出现脊线。
2.2 聚焦波束在圆孔缺陷处的散射特性
保持各圆孔缺陷不变,利用相控阵聚焦延时法则,合成聚焦于圆孔缺陷处的声束,简称聚焦波束。为比较聚焦声束与缺陷的交互作用规律,采用相同的延迟参数和激励信号,同时保持入射方向、聚焦点。图5展示了相控超声聚焦波束与圆孔缺陷交互作用的仿真结果图。

(a) 圆孔直径为0.5(b) 圆孔直径为1
(c) 圆孔直径为1.5(d) 圆孔直径为2
图4 相控超声平面波与圆孔交互作用的散射系数矩阵图
Fig.4 The scattering coefficient matrix chart of the plane wave interacted with the hole defects of different diameters
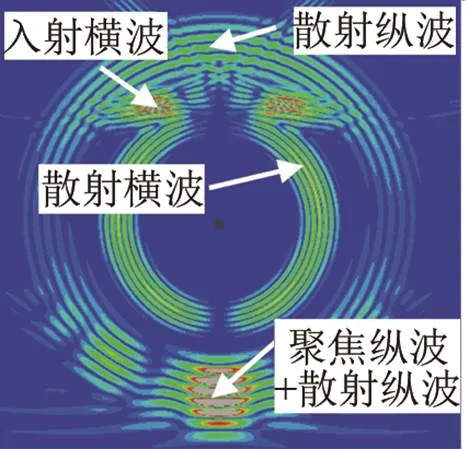
(a) 圆孔直径为0.5(b) 圆孔直径为

(c) 圆孔直径为1.5(d) 圆孔直径为2
图5 90°入射的相控超声聚焦波束与圆孔缺陷交互作用的仿真云图
Fig.5 Simulation images of phased array focused ultrasonic beam interacted with the hole defects of different diameters for 90° incidence
如图5所示,相控阵超声聚焦波在经过圆孔缺陷时,聚焦波束与圆孔缺陷交互作用产生了散射纵波和散射横波,散射纵波主要出现在反射区,在透射区的分布不明显,且随着圆孔直径增加,散射能量增加。此外,如图5(a)所示,由于在仿真相控阵阵元产生超声波的过程中,会同时激励出两种形态的超声波,即纵波和横波,因此在研究聚焦纵波与圆孔交互作用时,可以观察到入射的横波。
2.2.1 周向散射系数
提取聚焦波束入射到不同直径圆孔缺陷的周向散射系数,并绘制圆孔缺陷散射L模态的周向散射系数图,如图6所示。分析图6可发现,聚焦波束在圆孔缺陷处的散射L模态分布规律与平面波束入射时的散射场分布相似。
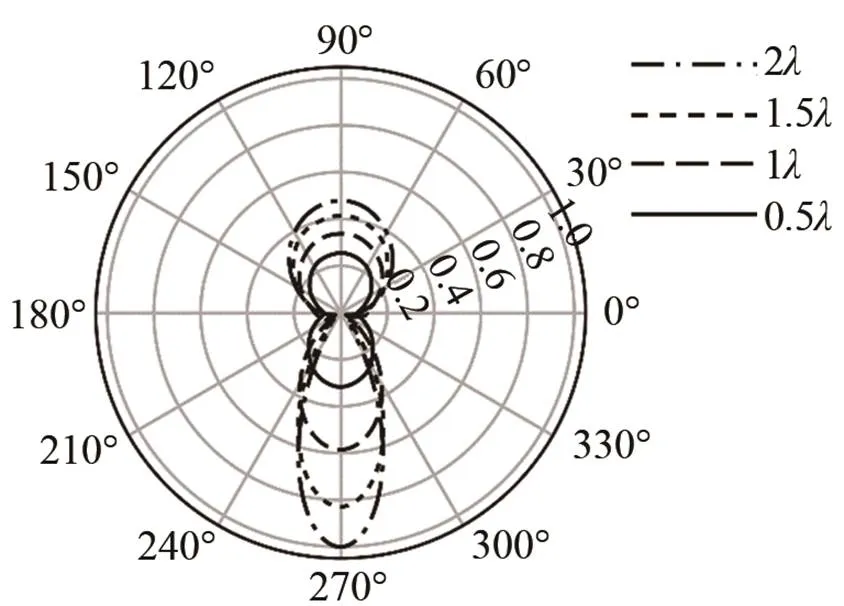
图6 聚焦波入射到圆孔缺陷的周向散射系数图
2.2.2 全散射系数矩阵
利用对称变换,获取聚焦波束入射到不同直径的圆孔缺陷的全散射系数矩阵,并分别绘制为全散射系数矩阵图,如图7所示。
从图7可知:(1) 散射矩阵图上的脊线、脊带、阱线和阱带均平行于散射矩阵的副对角线;(2) 随着圆孔直径的增加,关于散射矩阵副对角线对称的脊带变窄,能量变大;(3) 位于副对角线上的脊带随着圆孔直径增加逐渐变宽,能量逐渐增大。

(a) 圆孔直径为0.5(b) 圆孔直径为1
(c) 圆孔直径为1.5(d) 圆孔直径为2
图7 相控超声聚焦波束与圆孔交互作用的全散射系数矩阵图
Fig.7 The scattering coefficient matrix chart of the interaction of the focusing beam with the hole defects of different diameters
2.3 平面波与聚焦波在圆孔处散射特性的比较
对两种波束在同一缺陷处的周向散射系数进行同一尺度归一化处理,并绘制在同一个周向散射系数分布的直角坐标图中,分析平面波束和聚焦波束在同一圆孔缺陷处的散射场能量,如图8所示。

(a) 圆孔直径为0.5(b) 圆孔直径为1
(c) 圆孔直径为1.5(d) 圆孔直径为2

图8 不同入射波在圆孔处的散射系数统一归一化分布图
图8中,红色曲线代表聚焦波,蓝色曲线代表平面波。对比两种不同的相控阵超声波束分别从90°方向入射到不同直径圆孔的散射系数,可以看出聚焦波在圆孔缺陷处L-L模态的散射能量整体比平面波在圆孔处的散射能量大,特别是在90°与270°方向上聚焦波的散射能量明显大于平面波的散射能量。
在同一圆孔缺陷处,将两种不同的入射波的周向散射系数分别进行独立的归一化处理,对比分析两种不同波束在同一圆孔缺陷处的散射场能量分布情况,如图9所示。从图中可以看出:圆孔直径为0.5和1时,两种入射波在圆孔处的散射场分布曲线重合,即散射场的分布趋势相同;在圆孔直径为1和2时,两入射波在90°方向附近的散射能量略有差异,但散射场分布趋势相同,而在其他角度处的散射场分布相同。整体而言,聚焦波和平面波在圆孔缺陷处的散射L模态的分布趋势相同。

(a) 圆孔直径为0.5(b) 圆孔直径为1
(c) 圆孔直径为1.5(d) 圆孔直径为2

图9 不同入射波在圆孔缺陷处的散射系数单独归一化分布
综上分析,相控阵超声聚焦波和平面波与圆孔缺陷交互作用散射L模态的能量有明显差异,聚焦波在同一圆孔处的散射场能量明显高于平面波在圆孔处的散射场能量,但两者在同一圆孔缺陷处的散射L模态的分布趋势是相同的。
3 结论
本文对相控超声与圆孔缺陷交互作用的散射场分布特性进行了研究,得出的主要结论有:
(1) 圆孔缺陷处散射L模态的能量主要集中在正发射区和正透射区,且透射区的能量大于反射区能量,在与入射方向垂直的方向上,散射L模态的能量极其微弱;
(2) 同一相控阵超声声束入射下,圆孔缺陷随着直径的增加,散射场的分布趋势基本不变,但散射能量在增强;
(3) 相控阵超声聚焦波和平面波入射到同一圆孔缺陷时,聚焦波的散射场能量明显大于平面波的散射场能量,但两者在同一缺陷处的散射场分布趋势相同。
从以上研究结论中可发现,散射声场中包含有圆孔缺陷的特征信息,通过合成不同的相控声束能够改善检测分辨率,这为利用散射声场的分布特性进行圆孔缺陷反演重构,实现缺陷高分辨率成像及准确的定性定量分析提供了理论基础,对相控阵超声检测工艺的制定也具有重要的指导意义。
[1] 施克仁, 郭寓岷, 霍健, 等. 相控阵超声成像检测[M]. 北京: 高等教育出版社, 2010: 31-47. SHI Keren, GUO Yumin, HUO Jian, et al. Phased Array Utrasonic Imaging and Testing[M]. Beijing: Higher Education Press, 2010: 31-47.
[2] 周正干, 李洋, 周文彬. 相控阵超声后处理成像技术研究、应用和发展[J]. 机械工程学报, 2016, 52(6):1-11. ZHOU Zhenggan, LI Yang, ZHOU Wenbin. Ultrasonic Phased Array Post- processing Imaging Techniques: A Review[J]. Journal of Mechanical Engineering, 2016, 52(6):1-11.
[3] Drinkwater B W, Wilcox P D. Ultrasonic arrays for non-destructive evaluation: a review[J]. NDT&E International, 2006, 39(7): 525-541.
[4] Zetec, Inc. OVERIEW: Ultra-high performance phased array UT instruments[EB/OL]. [2016-05-18]. http://www.zetec.com/ products/ ultrasound/ instrumentation/ dynaray- dynaray- lite/ dynaray – key - features/.
[5] Holmes C, Drinkwater B W, Wilcox P D. Post-processing of the full matrix of ultrasonic transmit-receive array data for non- destructive evaluation[J]. NDT & E International, 2005, 38(8): 701-711.
[6] Pörtzgen N, Gisolf D, Blacquière G. Inverse wave field extrapolation: a different NDI approach to imaging defects[J]. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on, 2007, 54(1): 118-127.
[7] Hunter A J, Drinkwater B W, Wilcox P D. The wavenumber algorithm for full-matrix imaging using an ultrasonic array[J]. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on, 2008, 55(11): 2450-2462.
[8] 郑阳, 何存富, 周进节, 等. 超声兰姆波斜入射裂纹时的散射特性[J]. 机械工程学报, 2013, 49(4): 6-12. ZHENG Yang, HE Cunfu, ZHOU Jìnjie, et al. Scattering Characteristic of Lamb Wave at Crack with Oblique Incident[J]. Journal of Mechanical Engineering, 2013, 49(4): 6-12.
[9] 郑阳, 何存富, 周进节, 等. 超声 Lamb波在缺陷处的二维散射特性研究[J]. 工程力学, 2013, 30(8): 236-243. ZHENG Yang, HE Cunfu, ZHOU Jìnjie, et al. 2D scattering characteristics of Lamb wave at defects[J]. Engineering Mechanics, 2013, 30(8): 236-243.
[10] 郑阳, 周进节. 兰姆波在裂纹处的模态转换及散射特性研究[J]. 工程力学, 2014, 31(6): 21-29. ZHENG Yang, ZHOU Jìnjie. Mode Conversion And Scattering Properties of Lamb Waves Near Localized Cracking[J]. Engineering Mechanics, 2014, 31(6): 21-29.
[11] 吴斌, 张也弛, 郑阳, 等. 超声导波有限元仿真中吸收边界设置及参数[J]. 北京工业大学学报, 2013, 39(12): 1777-1783.WU Bin, ZHANG Yechi, ZHENG Yang, et al. Modeling and Parameters of Absorbing Boundary for Ultrasonic-guided Wave in FE Simulation[J]. Journal of Beijing University of Technology, 2013, 39(12): 1777-1783.
Research on the scattering characteristics of phased array focused ultrasound interacted with hole
ZHOU Jin-jie1, ZHENG Yang2, ZHANG Zong-jian2
(1. North University of China, School of Mechanical and Power Engineering, Taiyuan 030051, Shanxi, China;2. China Special Equipment Inspection and Research Institute, Key Laboratory of nondestructive testing and evaluation of AQSIQ, Beijing 100029, China)
Compared with the traditional detection methods, the sound beam focusing control ability of phased array technique makes the resolution, signal-to-noise ratio, sensitivity and other performances of ultrasonic phased array detection effectively improved. But at present, lack of understanding the interaction of phased array focused ultrasound with defects causes the current detection techniques impossible to achieve accurately qualitative and precisely quantitative analysis of defects. Therefore, this paper establishes a finite element model of one-dimensional linear ultrasonic phased array for the detection of hole defectsand studies the scattering characteristics of the acoustic field caused by the interaction of the phased array focused beam with the hole defect. The results show that the energy of L mode scattering of the hole is mainly focused on the positive reflection area and the positive transmission area, and the energy in the transmission region is greater than that of the energy in the reflection region, and energy is extremely weak in the direction perpendicular to the direction of incidence, almost no scattering energy. The L mode scattering is axial symmetrical distribution along the direction of incidence. For hole defects of different diameters, the larger the diameter, the greater the energy of the scattering obtains in the same direction. For the same diameter of the hole, the distribution of the scattering energy is the same for focusing wave or plane wave incidence, but the scattering energy of focusing wave is significantly higher than that of plane wave.
phased array; focus ultrasound; hole; scattering characteristics; scattering coefficient matrix
TB52+5 TB553
A
1000-3630(2017)-02-0147-05
10.16300/j.cnki.1000-3630.2017.02.009
2016-07-07;
2016-10-07
质检公益性行业科研专项(201410026)、(201510068), 质检总局科技计划项目(2014QK252)
周进节(1981-), 男, 湖北天门人, 博士, 讲师, 研究方向为超声无损检测与评价、传感器与检测仪器开发、自动化检测系统等。
郑阳, E-mail: zhengyangchina@126.com。

