一种高效的弱目标线谱检测算法

罗斌，王茂法，王世闯



一种高效的弱目标线谱检测算法

罗斌，王茂法，王世闯

(杭州应用声学研究所，浙江杭州310023)

为实现弱目标线谱检测，在自适应线谱增强(Adaptive Line Enhancement，ALE)算法的基础上，结合频域批处理技术，提出了一种能降低计算量的高效线谱检测算法——归一化频域批处理最小均方(Normalized Frequency-domain Block Least Mean Square，NFBLMS)算法；所提NFBLMS算法在权值迭代过程中，步长参数不受输入信号功率的影响。理论分析和数值仿真结果表明：相比于已有的线谱检测算法，NFBLMS算法能较好地解决ALE算法实时处理运算量问题，并可获得较高的系统增益，且其步长参数具有较强的鲁棒性，能同时兼顾算法的收敛速度和稳态误差。因此NFBLMS算法更适合实际工程应用。

线谱；自适应线谱增强；归一化频域批处理最小均方算法；鲁棒性

0 引言

随着减振降噪技术的不断发展，从强海洋背景噪声中检测出微弱的线谱信号，是近年来水声信号处理的一个重要研究内容[1]。水下目标线谱检测有经典功率谱估计与现代谱估计等方法[2]，在宽带噪声背景下检测出线谱信号是经典的声呐信号检测问题之一[3]。常规的声呐线谱检测方法大都采用细化傅里叶变换(Zoom Fast Fourier Transform，ZFFT)处理方法，该方法在低信噪比条件下提取线谱的效果较差[4]。自适应线谱增强是自适应信号处理技术的一个重要应用，最初由Widrow等人提出[5]，其最基本的算法采用的是最小均方(Least Mean Square，LMS)算法，它具有在低信噪比条件下较好地提取线谱的能力，且无需噪声参考信号就能自适应地将线谱信号从宽带噪声中分离出来。尽管该算法理论成熟、结构简单、稳定性好，但有其固有缺陷[6]，主要表现在：(1) 收敛速度和稳态失调量构成一对矛盾；(2) 收敛性能受输入信号功率的影响；(3) 计算复杂度较高，滤波速度通常难以满足实时要求较高的系统(如长线阵系统)。以上缺陷严重制约了该算法的工程实际应用。为此，本文在将频域批处理技术[7]应用到时域自适应线谱增强算法的基础上，提出一种高效的线谱检测算法，它不仅能大大减少自适应算法的运算量，使其更好地应用于长线阵系统，而且可以较好地兼顾自适应算法的收敛速度和稳态误差。

1 ALE算法

ALE是自适应信号处理技术的重要应用，它的主要功能是从宽带噪声中分离出窄带信号，进而对其进行检测跟踪。

1.1 算法原理

在线谱信号叠加宽带噪声时，无需独立地参考信号，只需将混合信号适当延时，利用最小均方自适应滤波器，当滤波器收敛时输出的将是两个不相关分量之和，一个来自于线谱成分输入分量经有限时延的维呐滤波后的输出，另一个来自于自适应过程中有关失调误差滤波器的输出。其结构框图如图1所示。

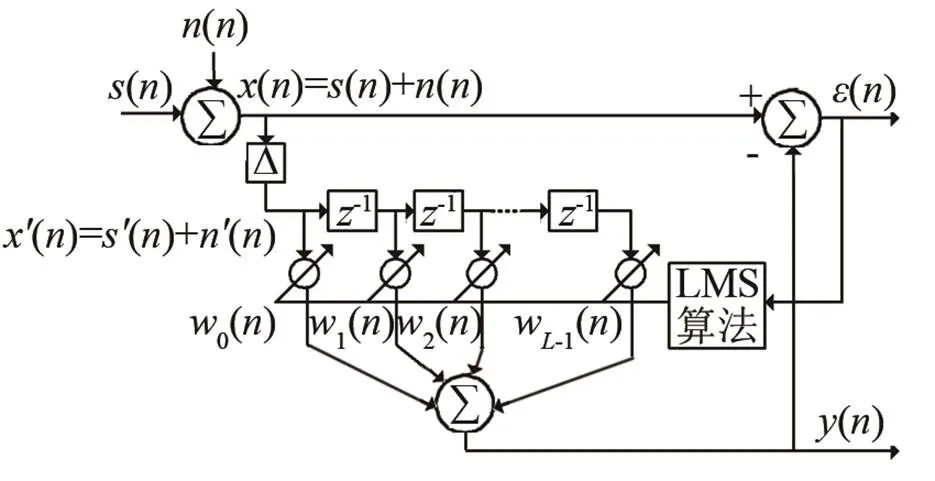
图1 ALE结构框图

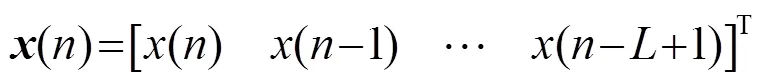
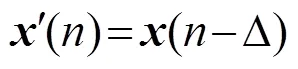
自适应滤波器的权矢量为

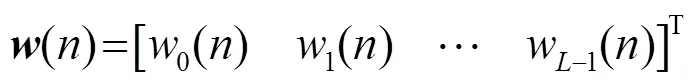
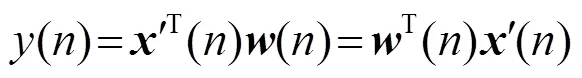
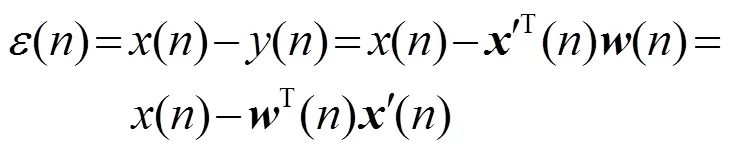
根据LMS算法的思想，ALE权系数更新表达式为

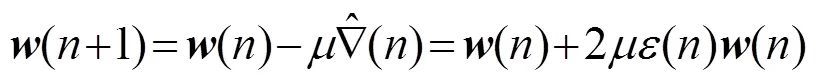
1.2 算法性能指标及性能分析

由于ALE算法是基于LMS算法的，因此其性能取决于LMS算法的性能。

衡量LMS算法性能的主要指标有算法的收敛性、收敛速度、稳态误差及计算复杂度；研究LMS算法性能一般都是围绕以上几个指标进行的。研究表明，该四项指标可以表示如下[8]：

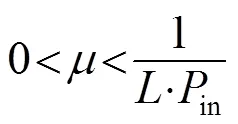
从②可看出，步长越大，LMS算法收敛速度越快；反之，LMS算法收敛速度越慢。

结合①和②可见，LMS算法收敛性能受限于输入信号功率，为保证最大输入功率时算法的收敛性，必须牺牲低输入信号功率时的收敛速度。

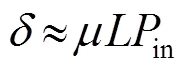
从④易得，LMS算法的计算复杂度与滤波器的阶数呈线性增长。

2 高效线谱检测算法

2.1 频域批处理技术

2.1.2 算法原理

为了减少LMS算法的计算量，可将频域批处理技术引入到LMS算法中，即频域批处理最小均方(Frequency-domain Block Least Mean Square，FBLMS)算法[9]，它很好地解决了ALE实时处理运算量问题，而且自适应滤波器阶数可达上千阶，可以获得很高的系统增益。FBLMS算法流图如图2所示。

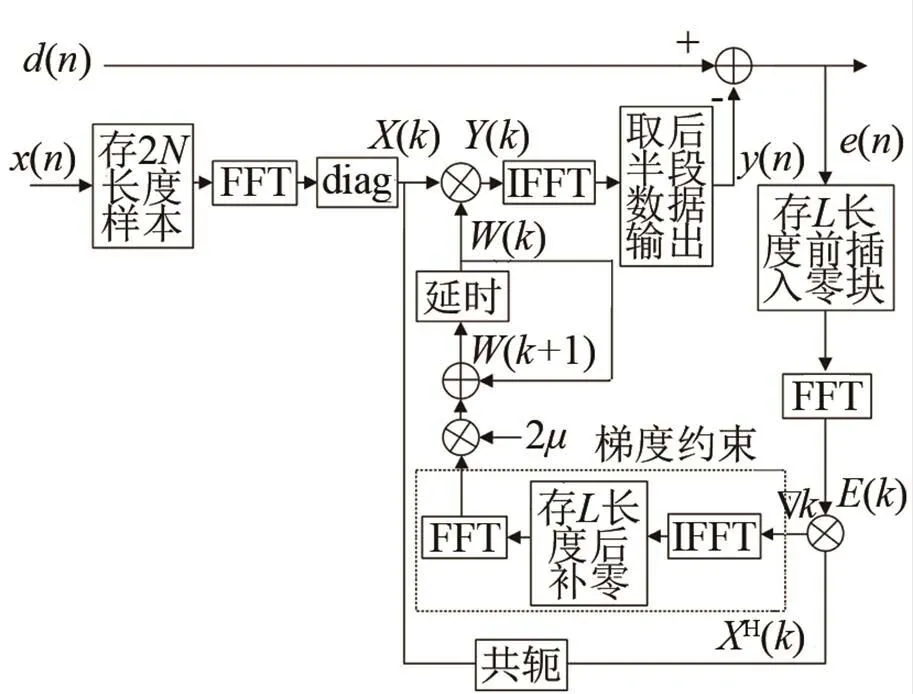
图2 FBLMS算法流图

图2中有，

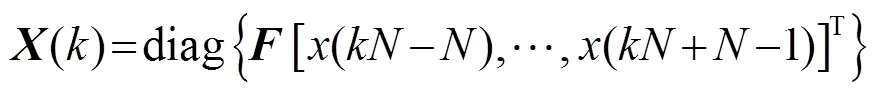
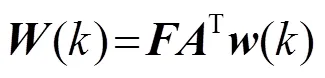
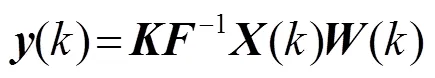
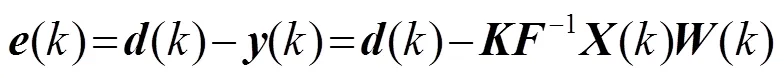
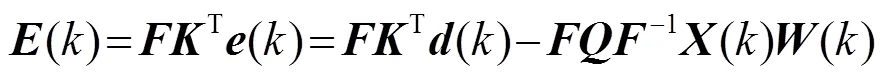
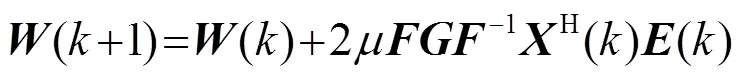
2.1.2 计算复杂度分析

算法的计算复杂度可以利用算法每次迭代的乘法次数来衡量。

当输入信号是实信号时，FBLMS算法与LMS算法的计算复杂度比值(Complexity Ratio，CR)为

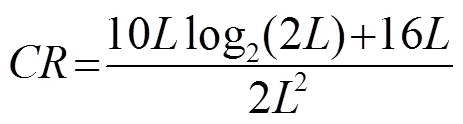
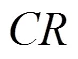
表1 FBLMS算法与LMS算法计算复杂度比值

2.2 快速收敛频域批处理技术

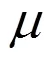
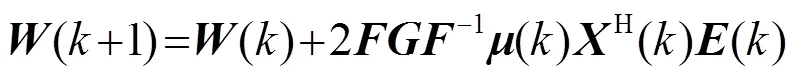
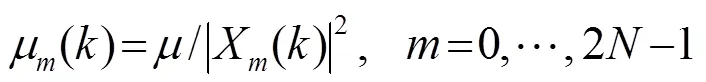
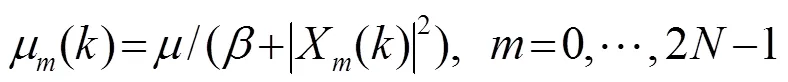
3 仿真分析研究

在对比FBLMS算法与NFBLMS算法线谱检测效果之前，本文先引进滤源块增益(Filtered Source Block Gain，FSBG)性能指标来描述频域批处理的性能，该指标的定义如下：

3.1 算法性能对比

下面通过对比在不同噪声环境下FBLMS算法与NFBLMS算法的性能，以此来说明本文算法的优越性。

3.1.1 高斯白噪声背景

仿真条件：源信号为正弦信号，频率为20 Hz，数据采样率为6 kHz，数据处理总点数为12 800。噪声为加性高斯白噪声，信噪比为0 dB。滤波器阶数为128。仿真研究结果如图3所示。

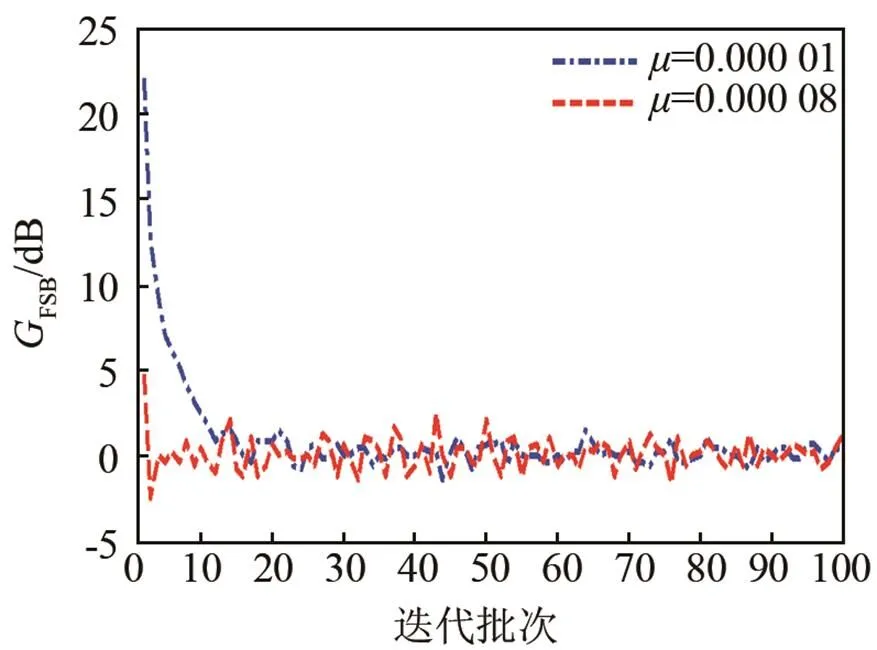
(a) 不同步长下FBLMS算法性能对比

(b) FBLMS算法与NFBLMS算法性能对比

图3 白噪声背景下FBLMS算法与NFBLMS算法性能对比

Fig.3 The performance comparison between FBLMS algorithm and NFBLMS algorithm in the white noise environment

3.1.2 高斯色噪声背景

仿真条件同3.1.1节，只是这里源信号叠加的是高斯色噪声背景。色噪声均值为0，方差为1，功率谱服从1/(表示频率，单位为Hz)分布。仿真研究结果如图4所示。

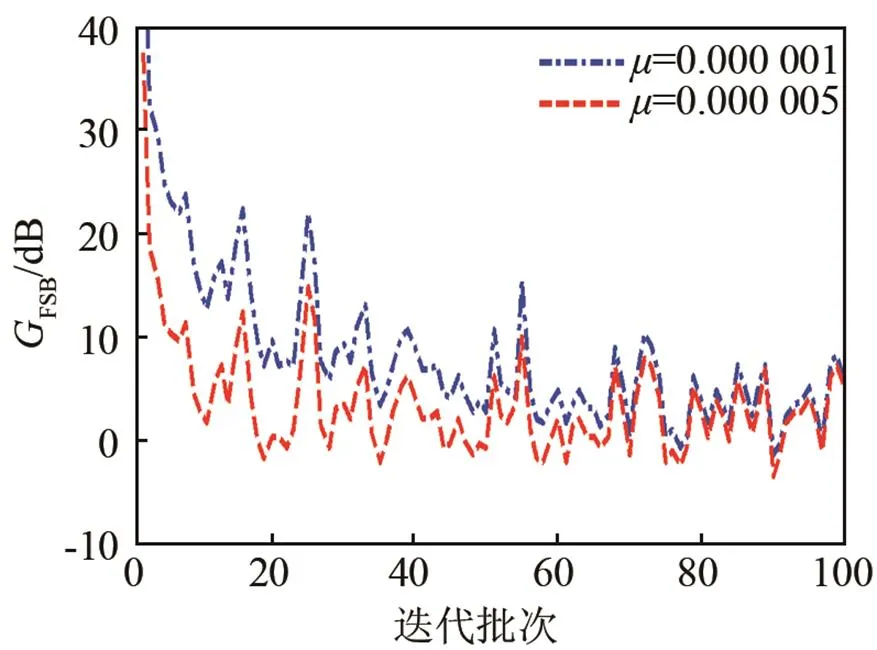
(a) 不同步长下FBLMS算法性能对比

(b) FBLMS算法与NFBLMS算法性能对比

图4 色噪声背景下FBLMS算法与NFBLMS算法性能对比

Fig.4 The performance comparison between FBLMS algorithm and NFBLMS algorithm in the color noise environment

3.2 线谱检测效果对比

为了更直观地展现本文算法在弱目标线谱检测中的效果，下面通过实例仿真给出采用FBLMS算法和NFBLMS算法的线谱增强检测结果。

仿真条件为：目标为频率600 Hz的单频信号，叠加宽带高斯白噪声背景，数据采样率为6 kHz，时间长度为100 s。频域批处理自适应滤波器阶数为1 024，信噪比分别为-25 dB和-30 dB。仿真结果如图5、6所示。

图5中可见，当信噪比为-25 dB时，目标线谱比较微弱，采用FBLMS和NFBLMS算法增强处理，均可有效检测出目标线谱。图6中，当信噪比降至-30 dB时，原信号的LOFAR谱已很难检测到线谱，通过FBLMS算法增强处理，大致能检测出线谱，但效果不是很明显。而采用NFBLMS算法增强处理后，效果明显，有利于准确检测线谱。

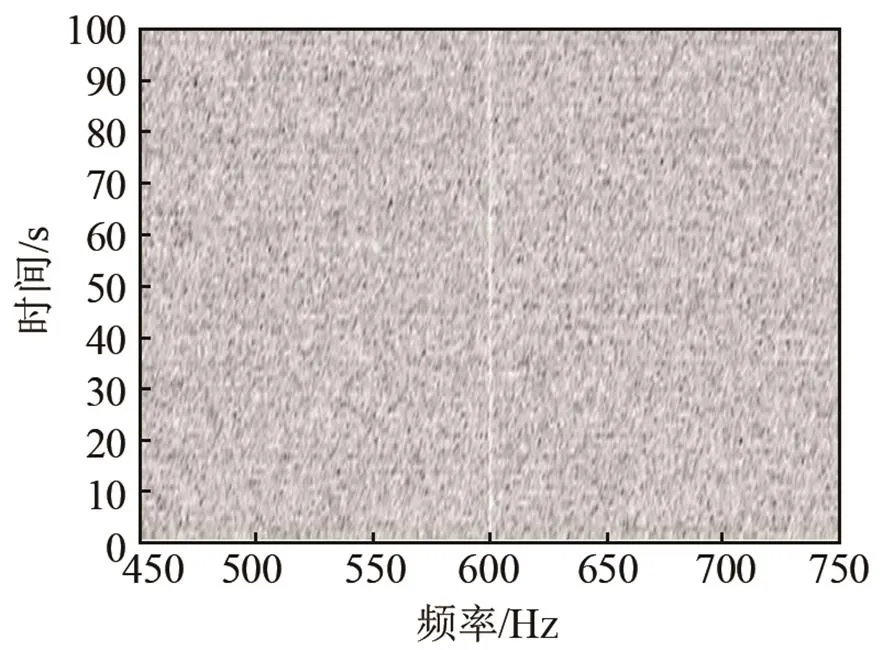
(a) 原信号LOFAR谱

(b) 采用FBLMS算法增强后信号LOFAR谱

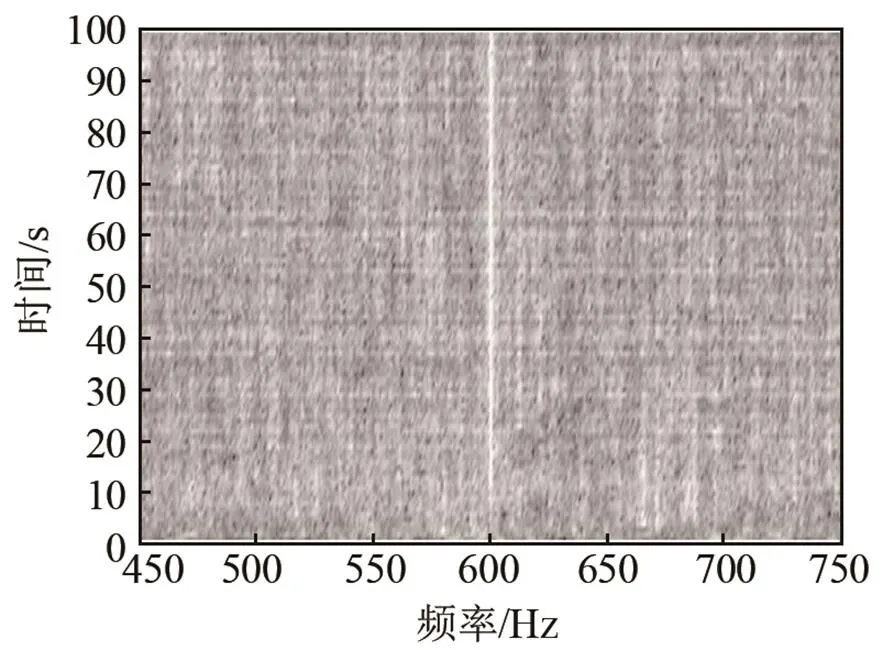
(c) 采用NFBLMS算法增强后信号LOFAR谱

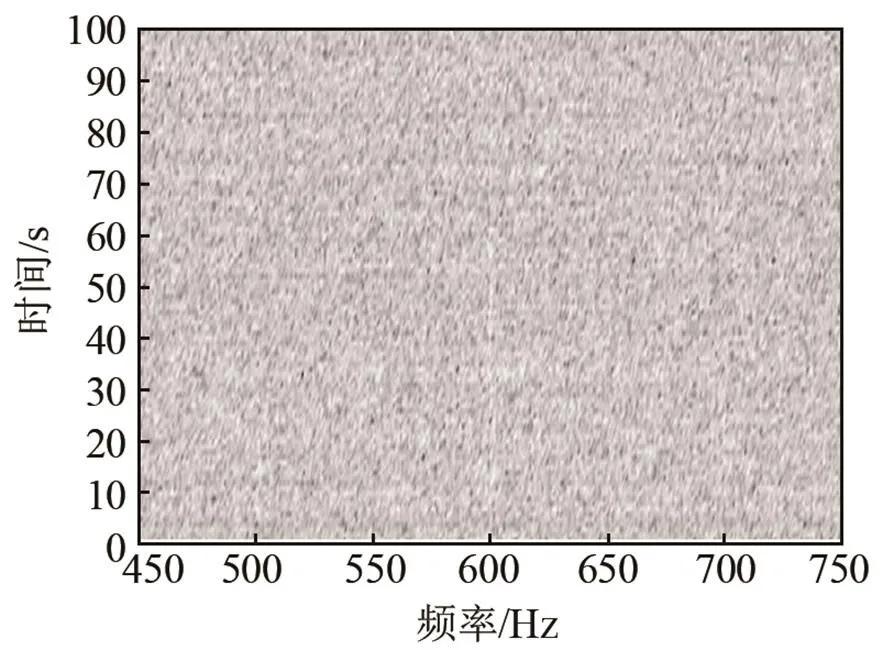
(a) 原信号LOFAR谱

(b) 采用FBLMS算法增强后信号LOFAR谱

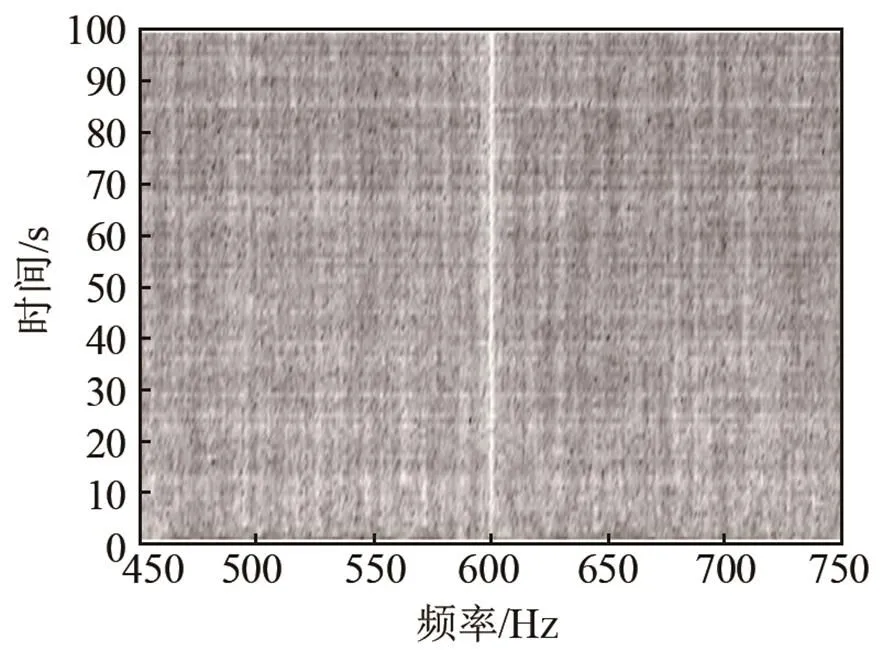
(c) 采用NFBLMS算法增强后信号LOFAR谱

综上所述，本文提出的高效线谱检测算法，能较好地检测出弱目标线谱，其在提高系统稳态增益的基础上，大大减少了算法的计算量及改善了算法收敛性能，并且还兼顾了稳态误差，为长线阵的工程实际应用提供了良好的理论基础。

4 结论

本文在分析常规ALE技术基础上，针对其计算量大难以工程实际应用的问题，引入了FBLMS算法，并提出了一种能降低计算量的高效线谱检测算法——NFBLMS算法。该算法不仅很好地解决了ALE算法实时处理运算量问题，在获得高系统增益的同时还兼顾了收敛速度和稳态误差。通过仿真分析研究，验证了NFBLMS算法的正确性及有效性，具有一定的实际工程意义及实用价值。

[1] 李启虎. 水声信号处理领域新进展[J]. 应用声学, 2012, 31(1): 2-9. LI Qihu. New advances of underwater acoustic signal processing[J]. Applied acoustic, 2012, 31(1): 2-9.

[2] 李启虎. 声呐信号处理引论[M]. 北京: 海洋出版社, 2000: 90-93. LI Qihu. Sonar signal processing[M]. Beijing: Ocean Press, 2000: 90-93.

[3] 王露, 雷波, 杨坤德. 基于谐波小波变换的舰船辐射噪声线谱提取方法[J]. 探测与控制学报, 2012, 34(3): 52-55. WANG Lu, LEI Bo, YANG Kunde. Based on harmonic wavelet transform method of line-spectrum extraction of ship radiation noise[J]. Journal of Detection & Control, 2012, 34(3): 52-55.

[4] Abutaleb AS. Adaptive line enhancement using a random AR model[J]. IEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(7): 1211-1215.

[5] Widrow B, Glover J R, McColl J M, et al. Adaptive noise canceling principles and applications[J]. Proceedings of IEEE, 1975, 63(4): 1692-1716.

[6] FAN Shuyu, DOU Heng. An improved variable step frequency-domain block LMS adaptive filtering algorithm[J]. Modern Electronic Technology, 2007, 258(19): 7-10.

[7] Lee J C. Performance analysis of frequency domain block LMS adaptive[J]. IEEE Transations on Circuits and Systems,1989, 36(2): 173-189.

[8] 威德罗, 斯蒂恩著. 自适应信号处理[M]. 王永德, 龙宪惠, 译. 北京: 机械工业出版社, 2008. Bernard Widrow, Samuel D Stearns. Adaptive signal processing[M]. WANG Yongde, LONG Xianhui, translate. Beijing: China Machine Press, 2008.

[9] Lee J, Huang H. On the step-size bounds of frequency-domain block LMS adaptive filters[J]. IEEE Signal Processing Letters, 2013, 20(1): 24-26.

[10] Shynk J J. Frequency-domain and multirate adaptive filter[J]. IEEE Signal Processing Mag, 1992, 12(1): 14-37.

A highly efficient weak target line-spectrum detection algorithm

LUO Bin, WANG Mao-fa, WANG Shi-chuang

(Hangzhou Applied Acoustics Research Institute, Hangzhou 310012, Zhejiang, China)

To detect underwater weak targets, we propose an efficient line spectrum detection algorithm based on adaptive line spectrum enhancement (ALE) and frequency-domain block processing. The proposed algorithm is termed as normalized frequency-domain block least mean square (NFBLMS) algorithm, which is not affected by the input signal power in the weight iteration process. Through theoretical analysis and numerical simulation, it is shown that compared with existing algorithms, NFBLMS algorithm can implement ALE in real time and obtain higher system gain, furthermore, NFBLMS algorithm is more robust to step size, thereby producing a tradeoff between the convergence speed and the steady-state error. Therefore, NFBLMS algorithm is more suitable for the engineering application.

line spectrum; Adaptive Line Enhancement(ALE); Normalized Frequency-domain Block Least Mean Square(NFBLMS) algorithm; robustness

TB566

A

1000-3630(2017)-02-0171-06

10.16300/j.cnki.1000-3630.2017.02.013

2016-07-14;

2016-09-20

罗斌(1989－), 男, 江西吉安人, 硕士, 研究方向为水声信号处理

罗斌, E-mail: luob_hz715@163.com。