基于噪声抵消技术的时延估计

郭昕钰，刘嘉琦，王良，宋志杰



基于噪声抵消技术的时延估计

郭昕钰，刘嘉琦，王良，宋志杰

(中国海洋大学信息科学与工程学院，山东青岛266100)

阐述了噪声抵消时延估计法(Time Delay Estimation based on Noise-canceling，TDENC)的基本原理，建立了TDENC分析的估计模型；并进行了大量仿真计算和初步海上试验。仿真结果表明：低信噪比且干扰噪声间相关性较强时，TDENC估计延时明显优于常规方法，但其主峰较宽；干扰噪声间彼此相关但信噪比高，估计时延精度则较差。海上试验结果和理论仿真一致。

时延估计；噪声抵消；最小均方误差；反转修正算法

0 引言

常规相关法是经典的时延估计方法，该方法利用相关函数峰值估计信号之间的延迟时间差，人们在不同方面做了大量研究工作[1-4]。在白噪声背景下，常规时延估计是最佳估计；而存在相关噪声时，常规估计性能变差。广义相关法[5]在对信号进行相关运算之前，对信号进行了加权处理；提高信噪比较高的信号频率成分，抑制低信噪比的信号频率成分，以达到提高信号整体信噪比的目的，最终提高时延估计的精度。B Widrow等[6]提出的自适应时延估计算法可以克服广义相关时延估计法加权固定的局限性。景思源等[7]根据平面四元法目标定位计算式，研究发现广义互相关时延估计算法具有精度高、稳定性好的特点。自适应时延估计算法可自动调节滤波器结构以及滤波器参数以达到最优准则[7-10]。

本文基于噪声抵消理论，提出一种新的时延估计方法——噪声抵消时延估计法(Time Delay Estimation based on Noise-canceling，TDENC)。基于自适应噪声抵消原理，对于彼此存在一定时延的两路同源信号，对信号进行抵消，当两路信号同步时，输出功率中信号残差最小，从而抵消后的输出功率最小，由此获得时延估计。通过对TDENC的仿真研究和海上实验数据处理，并与常规估计法进行对比，最后给出结论。

1 理论基础

1.1 自适应噪声抵消时延估计法(TDENC)

由文献[11]可知，自适应噪声抵消流程如图1所示。

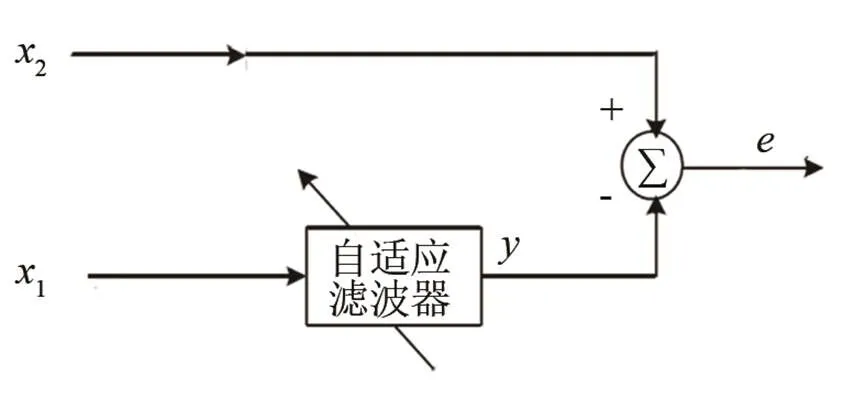
图1 自适应噪声抵消流程图

噪声抵消误差为

其中，为时间采样点，均方误差表示为

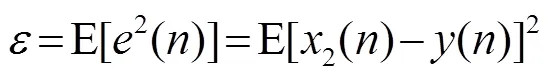
由于

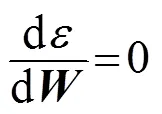
可得最优滤波器设计为

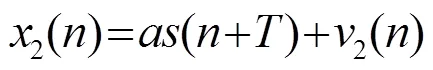
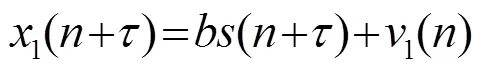
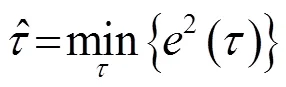
该估计过程中存在两步优化过程：

时延估计具体做法如下：

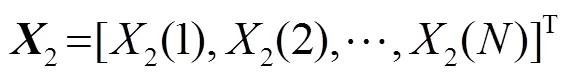
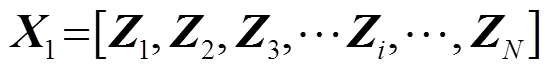
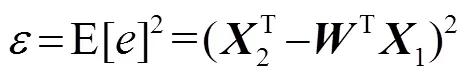
其中权向量为

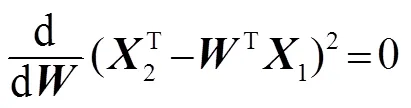
可得最优滤波器为

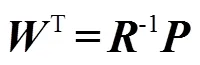
1.2 时延估计修正

由式(4)~(9)可看出，设计滤波器时利用一点对多点的方法进行抵消。由于选取参考点的差异，在估计过程中可能会出现偏移现象。针对这种现象，本文利用时间反转来修正偏差。修正思路为：对信号进行时间反转后再进行估计时，估计产生的偏移将会出现在相反方向，再对两次估计结果取平均处理，偏移即可修正。

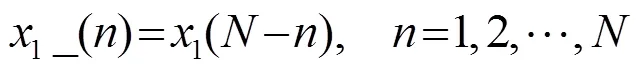
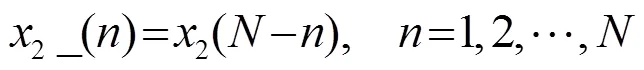
“其他同学的父母因为忙于工作不能到场，你们回去后也可以和父母说一声‘您辛苦了’，他们也会非常高兴的。”

2 数值仿真

本节通过数据仿真研究噪声抵消原理进行时延估计的性能。仿真条件为：主输入为1~2 kHz的限带白噪声信号，长度为8192点，采样率为48 kHz。将原始信号进行某一确定时延得到参考信号。为方便显示，将原始结果减去其最大值，再取绝对值，以使最小值变为最大值。

2.1 反转修正算法

原始算法和反转算法效果如图2所示。图2(a)中，信号时延设置在2 000点，背景噪声为白噪声。应用1.1节中的算法进行估计，常规方法最大值点出现的位置为2 000点，TDENC法最大值点出现的位置为2 003点，产生了较大的偏移。图2(b)给出了应用1.2节中反转算法的结果。其中，常规方法最大值点出现的位置为2 001点，TDENC法最大值点出现的位置为1996点，平均处理后，得到常规方法最大值在所在的位置为2000.5点，修正后的噪声抵消法最大值点出现的位置为1999.5点。该结果说明，反转算法能够有效修正1.2节中所提到的由于滤波器阶数影响所产生的偏移现象。另外，由图2可知，与常规相关时延估计法相比，在白噪声背景下，TDENC估计结果图主峰较宽，相对估计精度较差。该结论与引言中提出的常规相关时延估计在白噪声背景下为最优估计相一致。

(a) 原始算法

(b) 反转算法

图2 原始算法与反转算法效果图

Fig.2 Effect drawings of original algorithm and inversion algorithm: (a) original algorithm, (b) inversion algorithm

2.2 噪声相关性的影响

如果主输入和参考输入的长度均为1024点，是幅值为1的白噪声序列，时延为300点，对两路信号分别加入存在一定时延的相同白噪声序列作为相关干扰，相关干扰长度为256个点，是局部干扰，幅值为1.5，存在时延为310个点。再引入两路非同源白噪声作为背景噪声，幅值为0.2。噪声抵消时延估计算法中，滤波器阶数为5。

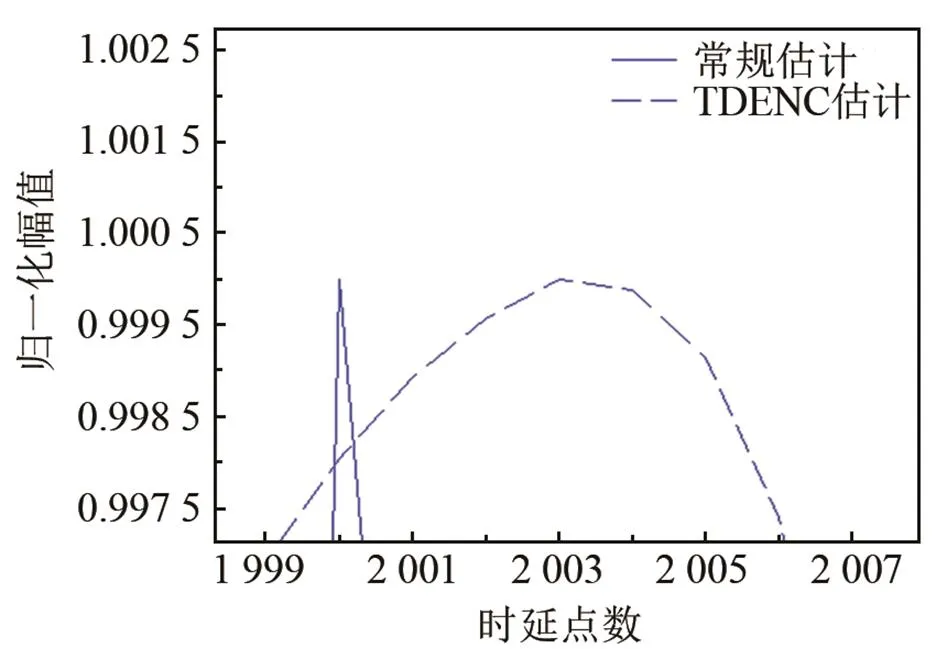
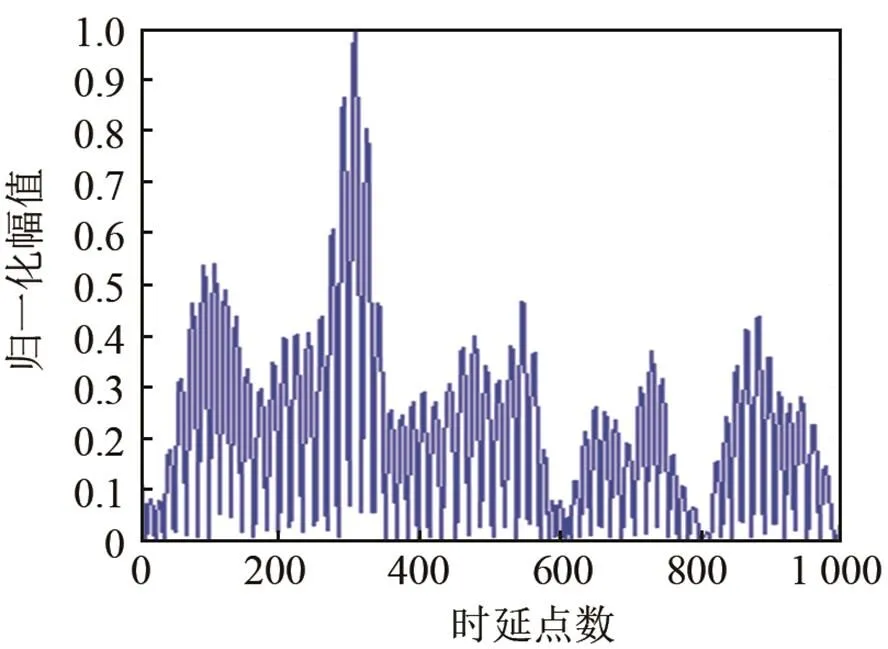
图3为常规相关时延估计和TDENC性能对比图。由图3可知，当存在相关噪声时，常规时延估计法受噪声影响较大，图3(c)为峰值所在位置的局部放大图，由于受到相关噪声影响，常规估计发生较大偏移，最大值出现在309点，利用TDENC进行估计时，最大值点出现在303点，相比于常规方法，偏移量更小。由此可知，TDENC可以有效减小相关噪声对估计结果的影响，提高了时延估计的准确度。

(a) 常规方法

(b) TDENC方法

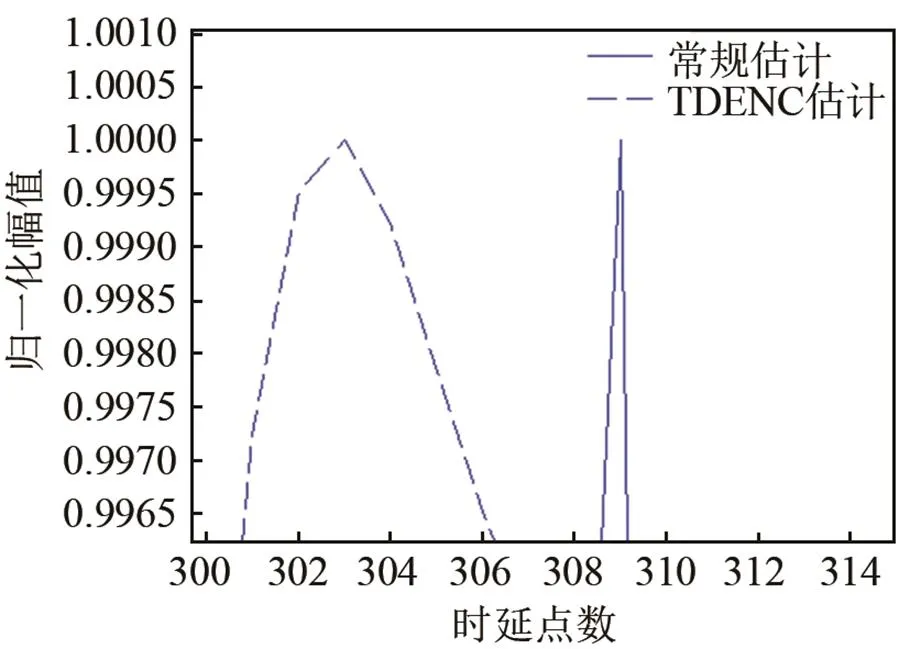
(c) 常规方法和TDENC方法时延估计性能对比图

2.3 带宽影响

将白噪声分别经4~5 kHz和2.5~6.5 kHz带通滤波后产生中心频率相同、带宽不同的两种限带信号，再将其一经2 000点延时构成两组信号，对其进行噪声抵消时延估计。

由图4可知，TDENC对带宽较宽信号的估计性能明显优于带宽较窄信号。在纵坐标处于半功率点(即0.5)时，1 kHz带宽对应的主峰半宽度为71个点，4 kHz带宽对应的主峰半宽度为23个点，主峰宽度随带宽增大而减小，同时，信噪比明显提高，从而提高了时延估计精度及稳定性。由此可见，TDENC法对宽带信号有较好的估计性能，得到了与1.1节中理论分析一致的结论。

(a) 带宽为1 kHz

(b) 带宽为4 kHz

图4 带宽对TDENC结果的影响

Fig.4 The influences of bandwidth on TDENC results

3 实验数据处理

3.1 常规相关法与噪声抵消法处理结果对比

分别采用常规相关和TDENC处理某一时刻数据，信号频段为1~8 kHz，信号长度为1 024点，滤波器阶数为8阶。实验中存在两个目标，目标1位于时延500点附近，较弱的目标2位于时延700点附近。

图5为320 s时，常规相关法和TDENC性能对比图，横坐标为时延点数，纵坐标为归一化后的幅值。由图5可知，当噪声相关性较强时，用常规方法进行估计时会出现较多虚警，难以准确识别。TDENC能较好抑制相关噪声，减少了虚警。图5(a)中，时延700点附近目标被淹没，在1400点、900点、250点附近出现较多虚警。图5(b)中，利用TDENC能有效抑制相关噪声，获得较高的信噪比处理增益，较准确估计出两个目标的时延点数。

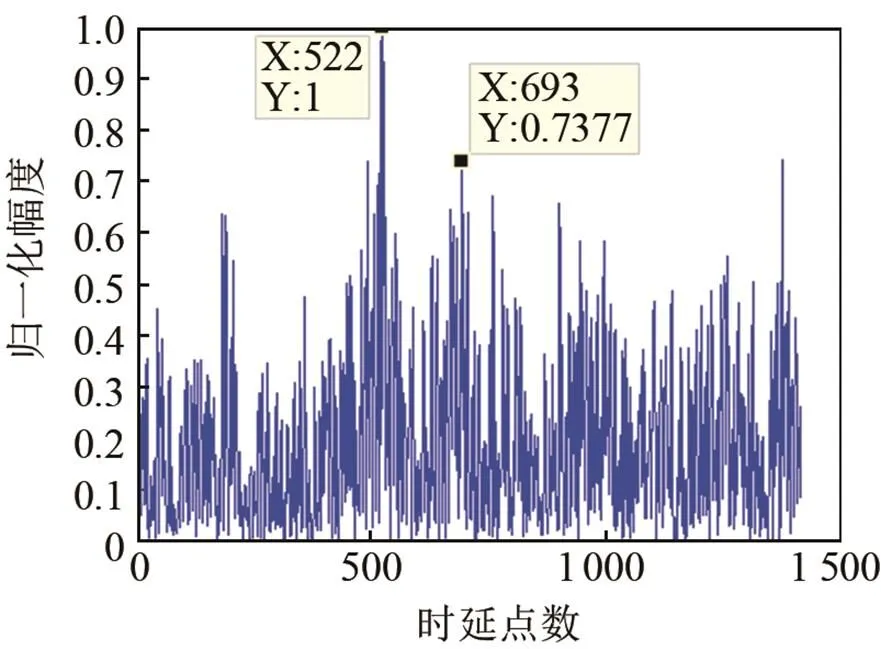
(a) 常规相关法

(b) TDENC估计性能对比图

图5 某一时刻(a)常规相关法和(b)TDENC估计性能对比图

Fig.5 Comparison charts of estimation performance (a) conventional correlation method, (b) TDENC

3.2 常规相关法与噪声抵消法估计精度对比图

选取某一时刻的数据，研究对目标2的估计精度，如图6所示。

(a) 常规相关法

(b) TDENC方法

图6 (a) 常规相关法与(b) TDENC时延估计结果随时间变化图

Fig.6 Variation of time delay estimation results with time (a) conventional correlation method, (b) TDENC

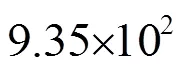
图7为截取前90 s两种估计结果历程图，图中20 s时刻对应的波形图见图5。由图7中可以明显看出，当存在较强的相关噪声干扰时，常规估计效果较差，目标淹没在背景噪声中，难以分辨。TDENC则能有效抑制相关噪声，获得较大的信噪比增益，使估计性能稳定，目标更加清晰。

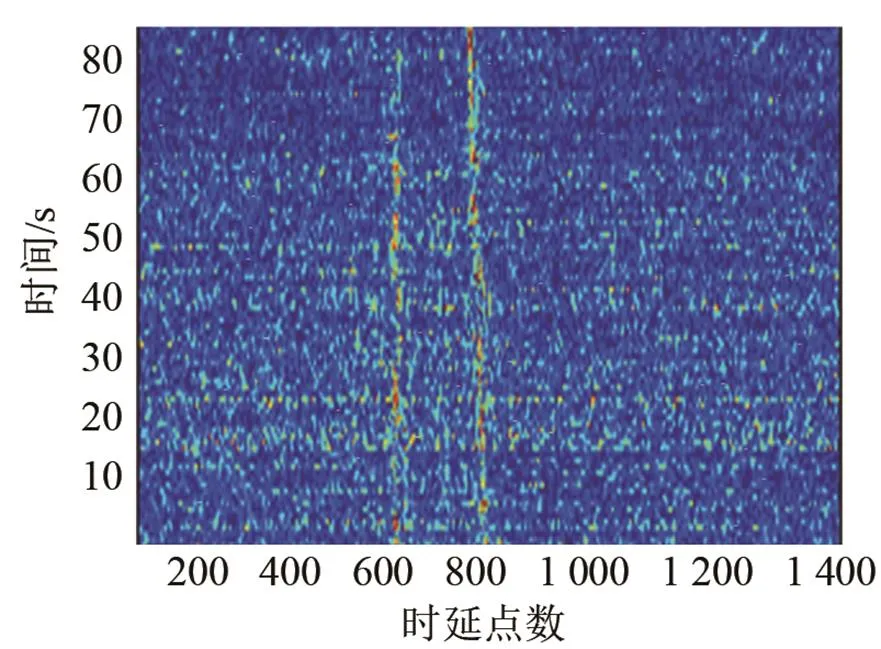
(a) 常规估计

(b) TDENC估计

图7 前90 s历程图(a) 常规估计(b) TDENC估计

Fig.7 Processing maps in the first 90 s (a) conventional correlation method, (b) TDENC

4 结论

本文以噪声抵消技术为理论基础，设计了一种时延估计方法——TDENC估计法。针对接收信号中存在相关噪声而导致常规相关时延估计性能变差的情况，TDENC能有效抑制相关噪声，从而提高时延估计精度。

本文通过仿真实验与海上数据处理，得出以下结论：

(1) TDENC对宽带信号有较好的处理结果，带宽越宽，估计性能越好。在3.3节仿真条件下，带宽增加为原来的4倍，主峰半宽度减少了67.6%。

(2) 相比常规检测，当噪声相关性较强时，TDENC方法能更有效地抑制相关噪声，获得更大的信噪比处理增益，提高时延估计精度。

(3) 高信噪比条件下，TDENC方法比常规方法时延估计精度低，表明它更适用于信噪比较低且干扰噪声相关性较强条件下的时延估计。在文中的海试条件下，性能提高了63.7%。

[1] Knapp C H, Carter G C. The generalized correlation method for estimation of time delay[J]. IEEE Trans. Acoust, Speech, Signal Processing, 1976, 24(8): 320-327.

[2] Messer H, Shor G. Passive time delay estimation in non-gaussian noise[J]. IEEE Trans, 1999, 7(9): 2531-2534.

[3] Xiao Lai, Hans Torp. Interpolation methods for time-delay estimation using cross-correlation method for blood velocity measurement[J]. IEEE Trans on Ultrasonics, Ferroelectrics, and Frequency Control, 1999, 46(2): 277-289.

[4] Stephenne A, Champagne B. A new cepstralperfiltering technique for estimating time delay under reverberant conditions[J]. IEEE Trans, 1997, 59(3): 253-266.

[5] 行鸿彦, 赵守国, 邸继征, 等. 广义相关时延估计算法的自适应实现形式[J]. 西安石油学院学报(自然科学版), 2001, 16(6): 47-51. XING Yanhong, ZHAO Shouguo, DI Jizheng, et al. Adaptive realizing form of generalized algorithm for time delay estimation[J]. Journal of Xi’an Petroleum Institute(Natural Science Edition), 2001, 16(6): 47-51.

[6] Widrow B, Steam S D. Adaptive signal processin[M]. Englewood. Cliffs: Prentice-Hall. Inc. 1993.

[7] 景思源, 冯西安, 张亚辉. 广义互相关时延估计声定位算法研究[J]. 声学技术, 2014, 33(5): 464-468. JING Siyuan, FENG Xi’an, ZHANG Yahui. Study of a generalized crosscorrelation time delay estimation based acoustic positioning algorithm[J]. Technical Acoustics, 2014, 33(5): 464-468.

[8] 詹国强, 吴正国. 一种新的变步长LMS自适应滤波算法[J]. 海军工程大学学报, 2006, 18(2): 109-112. ZHAO Guoqiang, WU Zhengguo. Anovel variable step size adaptive filtering LMS Algorithm based on sample function[J]. Journal of Naval University of Engineering, 2006, 18(2): 109-112.

[9] 冯桂, 张继贤. 噪声的分布层次分析及其自适应滤波算法[J].测绘科学, 2000, 25(3): 12-13. FENG Gui, ZHANG Jixian. The study of noise hierarchical distribution and corresponding adaptive filtering algorithms[J]. Science of Surveying and Mapping, 2000, 25(3): 12-13.

[10] Chang C Y, Shyu K K. Active noise cancellation with a fuzzy adaptive filtered-x algorithm[J]. IEE Proc. Circuits Devices Syst. 2003, 150(5): 416-422.

[11] 曹斌芳. 自适应噪声抵消技术的研究[D]. 长沙: 湖南大学, 2007. CAO Binfang. Research on adaptive noise cancelling technology[D]. Changsha: Hunan University, 2007.

Time delay estimation based on noise-canceling

GUO Xin-yu, LIU Jia-qi, WANG Liang, SONG Zhi-jie

(College of Information Science and Engineering, Ocean University of China, Qingdao 266100,Shandong, China)

A time delay estimation method based on noise canceling called TDENC (Time Delay Estimation based on Noise-Canceling)is proposed to improve the time delay estimation performance when the background noise is correlative. A TDENC model is formed firstly in this paper, and then computer simulations are carried out to study the performance and applicable range of TDENC. Simulation results show thatin the case of low SNR and strong correlation between noises, TDENC method is obviously superior to the conventional methods, but the main lobe is broad. However, when SNR is high, the performance of TDENC is worse than the conventional method. The experimental data processing results agree well with the simulation.

time delay estimation; noise-canceling; Minimum Mean Square Error(MMSE); inversion correction algorithm

TN911.7

A

1000-3630(2017)-02-0177-06

10.16300/j.cnki.1000-3630.2017.02.014

2016-07-29; 修改日期:2016-10-22

郭昕钰(1993－), 女, 山东东营人, 硕士研究生, 研究方向为水声信号处理。

郭昕钰, E-mail: 453237740@qq.com。