基于分块矩阵变换的线性分组码盲识别*
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
基于分块矩阵变换的线性分组码盲识别*
赵 亮**,张天骐,杨 强
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
为了解决传统矩阵分析方法存在的误码扩散问题,提出了一种基于分块矩阵变换的线性分组码盲识别方法。首先,将截获序列按照估计码长构造出分析矩阵,将分析矩阵分块后分别进行矩阵下三角变换;然后,以各列列重为度量,根据相关列重量的统计分布特性设置相关列阈值,并统计出符合阈值的相关列的个数,当相关列的个数最大时即为真实码长的情况。该方法还可以识别码字同步点,识别方法简单。理论分析及仿真结果表明,该识别方法的容错性能较好,在误码为5%的条件下,对(15,7)线性分组码的正确识别率依然能达到80%。
线性分组码;盲识别;分块矩阵变换;相关列
1 引 言
分组码包括线性分组码和非线性分组码,线性分组码是重要的一种,它具有良好的检错和纠错能力。在实际工程领域,信息传输过程中不可避免地要受到信道中噪声的影响,使传输的信息发生误码。为了提高通信系统的可靠性,可引入纠错编码的方法,对需要传输的信息进行编码,为其加入一些冗余校验比特,使其具有一定的抗误码能力。在信息对抗和电子侦察领域,如何通过截获的数据,快速准确地识别出传输数据的编码参数,进而获取信息,是一个具有重要现实意义的问题[1-3]。
文献[4]对分析矩阵求秩获取码长和码率,但只考虑理想信道而没有考虑误码的影响。文献[5]利用汉明距离出现的概率分布和随机序列的汉明距离出现的概率分布相比较,偏移量越大,说明线性约束的关系越强,可以识别码长和码字起点,进而识别生成矩阵;且与码重分析法相比,识别结果清晰,在真实码长位置才出现峰值,其他位置不会出现峰值。但上述两种方法都未考虑误码的影响。文献[6]提出基于欧几里得算法的最大公因式识别算法,该方法在有误码时需要大量的分析数据。文献[7]首次提出码根信息熵的概念,利用码根统计的方法解决了误码条件下的二进制本原BCH码盲识别问题,但识别的计算量较大。文献[8]利用码根信息熵的思想获得码长以后,根据有限域同构的原理,利用统计得到的码根经过有限域乘法并化简直接求出BCH码的生成多项式,但计算复杂度较高。文献[6-8]中的识别方法只限于对线性分组码的子类BCH码的识别,适用范围比较局限。文献[13]首次引入数据挖掘中的关联规则挖掘算法,但容错性能较差,不能很好地适用于在高误码率下对线性分组码的盲识别。
针对上述问题,本文提出了一种基于分块矩阵变换的识别方法。首先根据估计码长,对截获序列构造分析矩阵,再将分析矩阵进行分块,在每个矩阵块中做矩阵变换,以达到抑制误码扩散的目的。在无误码的情况下,校验位所在的列可以被化为全零列,称其为相关列,信息位所在列为独立列。然后以各列的重量为度量,根据相关列和独立列的列重的统计分布特性,设置阈值判断各列是否为相关列,统计相关列的个数,当相关列个数最大时,即为真实码长的情况。码长识别出来以后,通过循环移位,按照码长识别的方法,当相关列个数最大时即为正确码字起点。本方法适用于多种码率的线性分组码参数识别,运算复杂度相对较低,且容错性能较好。
2 线性分组码盲识别原理
定义1[2]在GF(2)上的2k个k维信息向量可以生成2k个二进制的n维向量,它们的集合构成(n,k)线性分组码。k维信息向量也叫做信息位,生成的n维向量叫做其对应的码字。线性分组码构成了GF(2)上n维线性空间的k维子空间。
由于常用的线性分组码码字都是系统码,所以c=(c1,c2,…,ck,…,cn)的前k位就是信息位u=(u1,u2,…,uk),码字的后k位(c1+k,c2+k,…,cn)就是校验位。对线性分组码有
c=uG。
(1)
式中:G表示(n,k)线性分组码的生成矩阵。
生成矩阵确定了信息位和校验位的线性映射关系,不同的编码方式使用的生成矩阵不同,也就有不同的映射关系,但是(n,k)线性分组码的2k个码字必定由对应的k个信息比特位构成的独立向量线性表示。由此可知,码字c中的(n-k)位校验位是k位信息位的线性组合。因此,将码字按真实码长排列成矩阵形式,进行矩阵变换以后,校验位对应的列将被化为全零列,称校验位所在的列为相关列,信息位所在列为独立列。在真实码长和码字正确起点时,码字之间的信息位和校验位对齐,可以被化为全零列的列数最多,即此时相关列最多。而在非真实码长时信息位和校验位未对齐,不存在相关列,在无误码时就没有能够化为全零的列存在;有误码时,不存在0的比例比1的比例大的列。本文就是基于这个思想提出了码长和同步点的识别算法。本文中考虑的信息传输信道是二进制对称信道(Binary Symmetric Channel,BSC),这是一种无记忆信道,即二进制符号数据序列在传输过程中前后出现的错误是相互无关的。对于线性分组码,其码字之间的约束关系仅限于码长范围以内,不受信道中的误码影响。
传统的矩阵分析方法,将矩阵变为下三角矩阵的操作,对矩阵整体进行行变换和列变换,虽然互换行、列只是交换码字或者码元的位置,均不会改变信息位和校验位的线性约束关系,也不会造成误码扩散,但是行之间的模2加会造成误码在码字之间传播,列之间的模2加会造成误码在码字内的扩散。基于传统方法改进后提出的高斯列消元方法,在矩阵变换时只使用列操作,避免了错误码元在码字之间的传播,但依然存在较为严重的误码扩散现象。为了抑制这种现象,可以利用分块处理的思想,为分析矩阵按行分块,分别在每个矩阵块内进行矩阵变换,误码影响只在窗内传播并不影响其他窗内的码字,而且矩阵块的规模越小,误码传播范围就越小。
算法步骤如下:


Step3 记X1为对A1处理后的下三角矩阵。依次对At(t=2,3,…,c),进行上述处理,直到处理完Ac。
Step4 记录经过矩阵变换后的矩阵X=(X1,X2,…,Xc)T,并统计其各列的重量W=(w1,w2,…wc)。
3 统计特性分析及阈值的设置
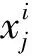
当xj是相关列时,
(2)
(3)
则xj的重量wj服从伯努利分布B(m,(1-(1-2pe)wb)/2),wb是其对偶向量的重量;
当xj是独立列时,
(4)
(5)
则xj的重量wj服从伯努利分布B(m,1/2),其中,
(6)
取码字个数m=400,pe=0.12,wb=4,相关列和独立列的列重wj的概率分布图如图1所示。
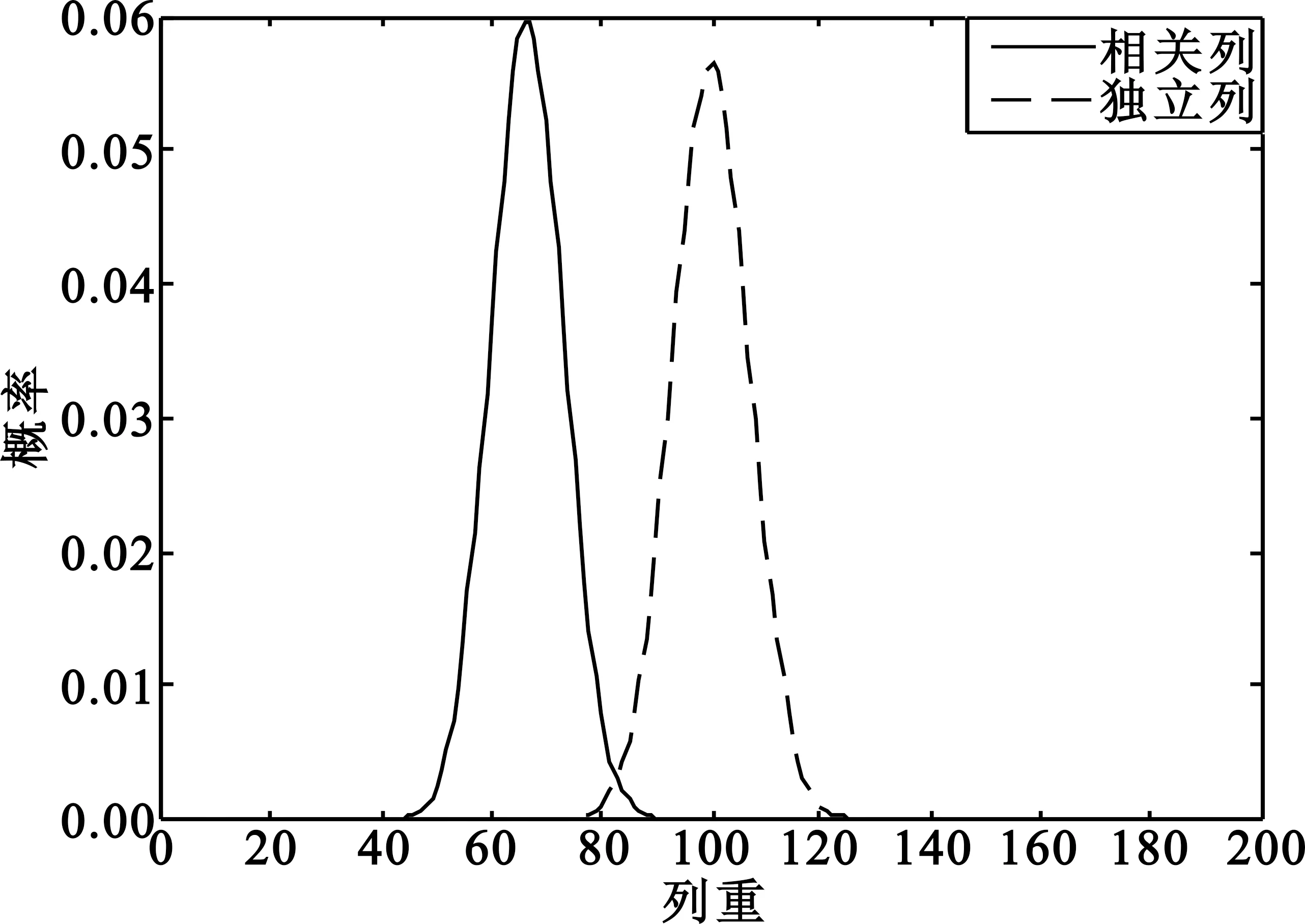
图1 相关列和独立列的重量wj对应的概率分布图Fig.1 The corresponding wj′s probability distribution of dependent column and independent column
在每个估计码长下,对矩阵X进行循环移位,记每次移位的矩阵A(n0,d),d为移位数,且0≤d≤n-1。
定义识别的数学模型:
φ(j)=wj/(m/2)=2wj/m。
(7)
经过分析可以知道,φ(j)越小,xj的重量越小,1的比例越低,也越符合相关列的情况;反之,则符合独立列。因此,设置阈值T,当φ(j)≤T时,判定为相关列;反之则判定为独立列。对每个移位矩阵A(n0,d)都有相关列的集合:
{j1,j2,…,jΘn0,d|φ(j)≤T} 。
(8)
式中:ji表示满足阈值T的列所在位置。当真实码长和正确同步点时,集合的基数Θn,d达到最大,即相关列的数目最多。
对每一个估计码长下相关列个数集合的Θn,d归一化处理,有
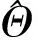
(9)
可知,当n0=αn(α∈+)时,n0为极大值。取α=1时的n0为码长,即第一个极大值出现的位置就是真实码长的位置。
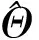
对最优阈值的求解如下:
令虚警概率为Pfa,漏警概率为Pnd,则
(10)
(11)
令
P=Pfa+Pnd,
(12)
定义阈值T使得概率P达到极小值,得
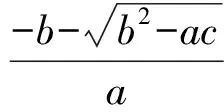
(13)
其中:

(14)
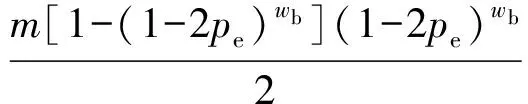
(15)
c=m[1-(1-2pe)wb](1-2pe)wb-
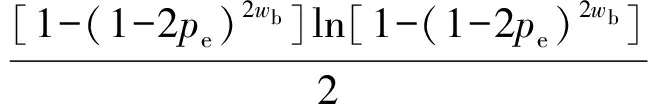
(16)
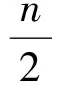
(17)
对于服从标准正态分布的变量x~N(0,1),数学上认为|x|≥0.39是不可能事件,所以需要有

(18)
则取阈值为
T=min(T1,T2) 。
(19)
综合以上分析,本文算法的流程图如图2所示。

图2 算法流程图Fig.2 Flow chart of the proposed algorithm
4 仿真分析
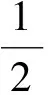
对(7,4)循环码进行码长和同步点的识别,仿真参数为:数据截获长度300 bit,同步点5,误码率0.02。识别结果分别如图3和图4所示。
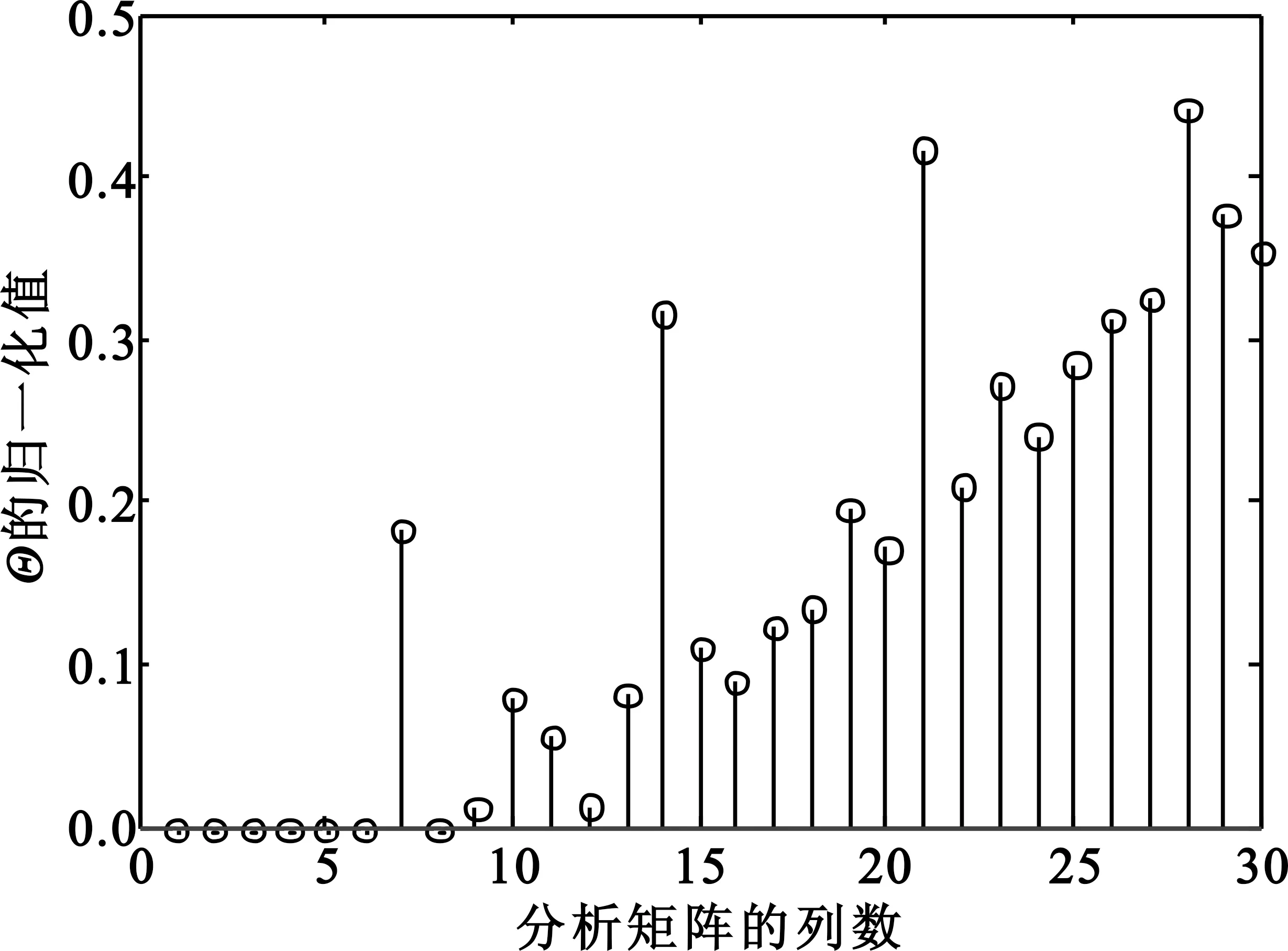
图3 (7,4)循环码的码长识别结果Fig.3 Recognition result of (7,4) cyclic code
图4 (7,4)循环码码字起点识别结果Fig.4 Recognition result of the code start bit for (7,4) cyclic code
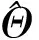
识别出正确码长后,按正确码长构造分析矩阵,经过矩阵变换后,统计各种移位情况下的Θ值。从图4可以看出,Θ的值在移位值为5时取得最大值,识别码字起点为5,识别结果正确。
对(15,7)循环码进行识别,仿真参数为:截获数据长度300 bit,同步点13,误码率0.02。码长和同步点的识别结果分别如图5和图6所示。
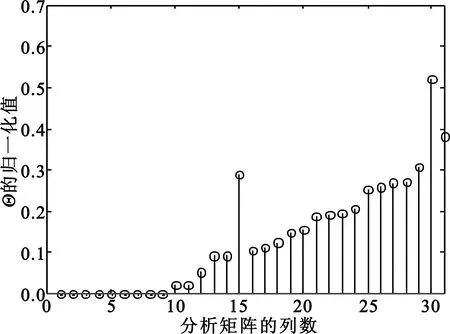
图5 (15,7)循环码的码长识别结果Fig.5 Recognition result of(15,7) cyclic code
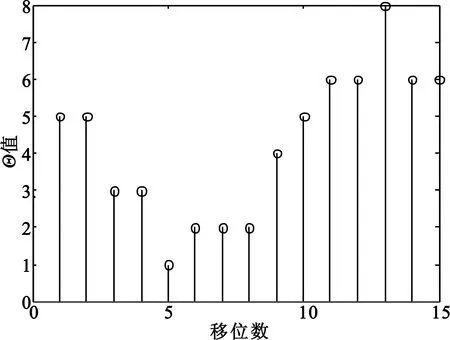
图6 (15,7)循环码码字起点识别结果Fig.6 Recognition result of the code start bit for (15,7) cyclic code
识别出码字长度为15以后,继续估计码字起始点,如图6所示,在移位数为13时,Θ取得最大值,识别码字起点为13,识别结果正确。
从以上(7,4)循环码和(15,7)循环码的识别情况可以看出,当识别码字起点时,Θ取得最大值所在的移位数即为正确码字起点。但是,有时识别码字起始点时,Θ的最大值不唯一,此时就需对其进行多次识别然后取均值,找到最大值唯一的情况。
在pe=0.02下对序列进行(15,11)循环码编码,识别出码长后,识别码字起点的结果如图7所示。
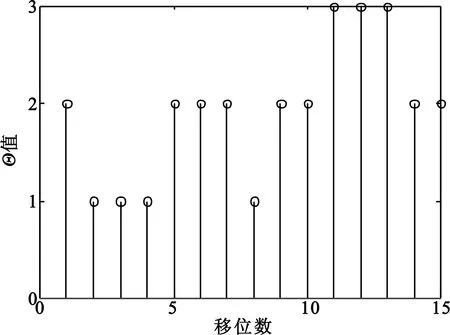
图7 (15,11)循环码码字起点识别结果Fig.7 Recognition result of the code start bit for (15,11) cyclic code
此时,最大值不止一个,在11、12、13处均有最大值。选取这三处的移位情况做多次求解Θ的值后做均值,次数为15次时识别结果如图8所示。
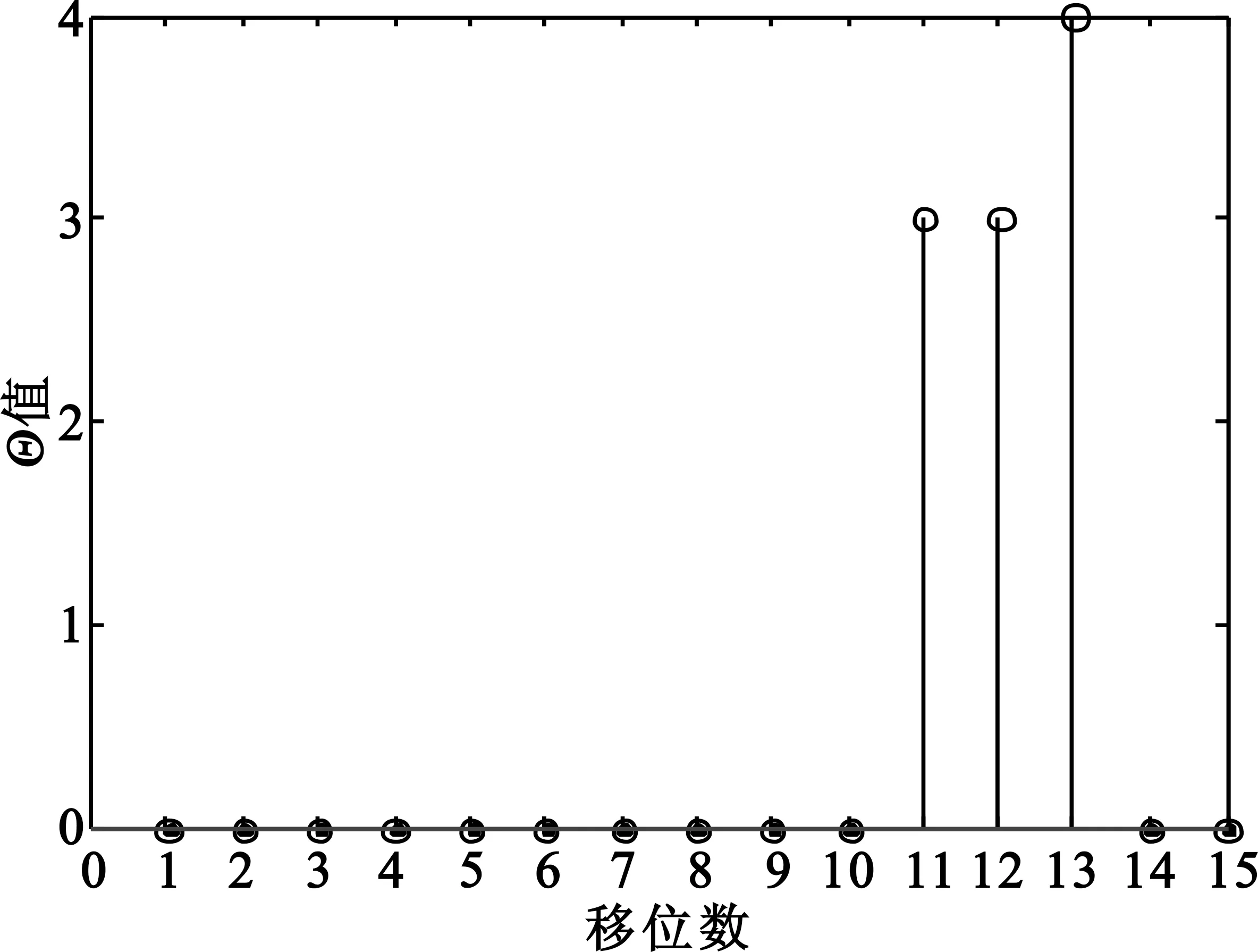
图8 (15,11)循环码码字起点最后的识别结果Fig.8 Final recognition result of the code start bit for (15,11) cyclic code
下面针对不同码长的码字进行仿真分析,分别选取(7,3)循环码、(7,4)循环码、(15,7)循环码、(15,11)循环码进行分析,在不同误码率下做100次蒙特卡洛仿真,仿真参数设置如表1所示,识别概率见图9。
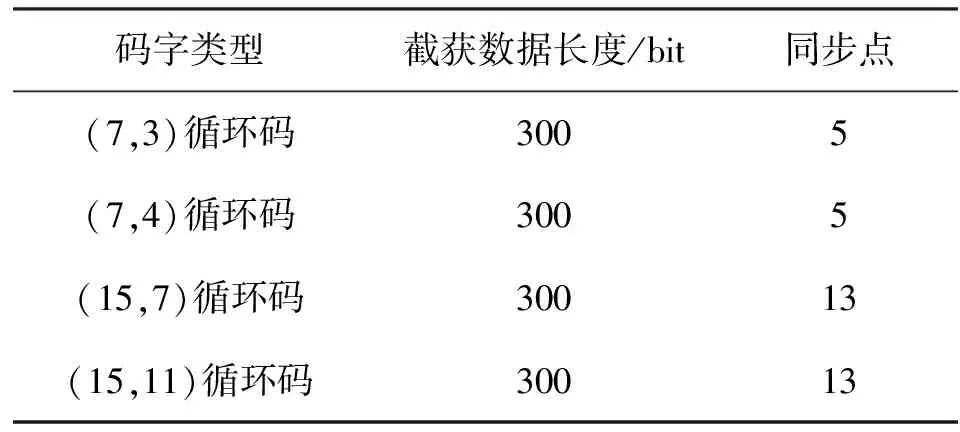
表1 对不同码型识别性能实验的仿真参数Tab.1 Simulation parameter
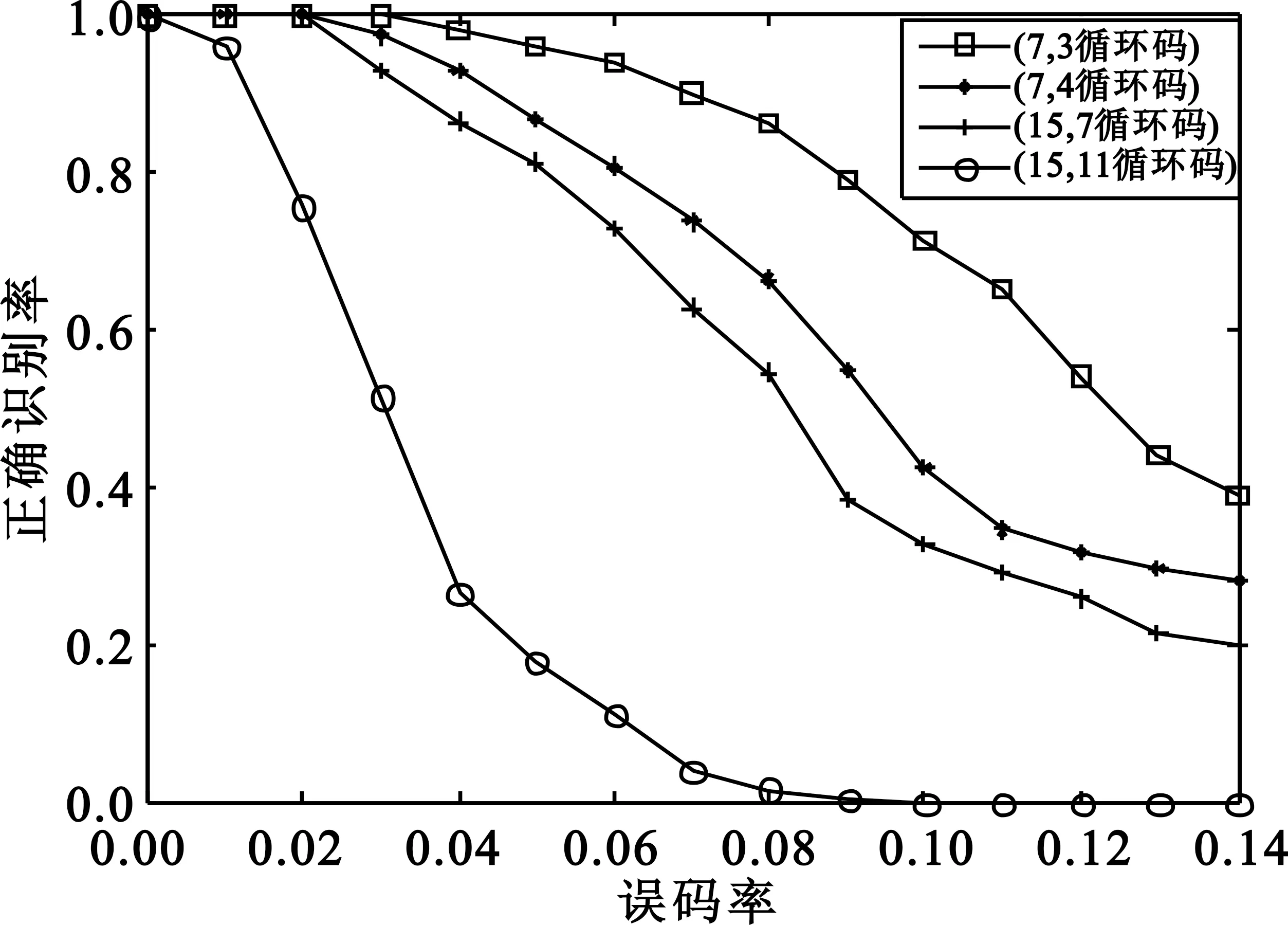
图9 算法在不同误码率下的正确识别率Fig.9 The correct recognition rate of the algorithm under different bit error rate
从图9可以看出,(7,4)循环码、(7,3)循环码比(15,7)循环码、(15,11)循环码的识别效果好,说明对于本算法来说,码长越长,识别效果越差。(7,3)循环码、(15,7)循环码分别比(7,4)循环码、(15,11)循环码的识别效果好,说明码率越高识别效果越差。对于(7,3)循环码,在误码率为0.09时识别概率依然可以达到80%以上。
图10给出了3种算法对(15,7)循环码在不同误码率情况下的识别概率对比结果。仿真参数设置同前。与文献[11]的性能相比,在误码率低于0.06时,文献[11]的识别效果略优于本文算法,但随着误码率的提高,识别效果明显比本文算法要差,且考虑文献[11]的计算量较本文算法要大得多,因此本文算法依然具有优势。与文献[12]中所提的传统矩阵分析算法相比,本文识别效果具有明显的正确识别优势,而且与文献[13]中所用的关联规则算法识别性能优势更加明显。在误码率为0.05时,本文算法的正确识别率可以达到80%,而文献[12]仅能达到50%左右,文献[13]则仅能达到20%。本文算法对p×q阶矩阵进行处理时,因为只需要进行O(N3)模2加法运算,其中N为分析矩阵的最大列数。因此,本文算法在性能和复杂度上与已有算法相比具有较为明显的优势。
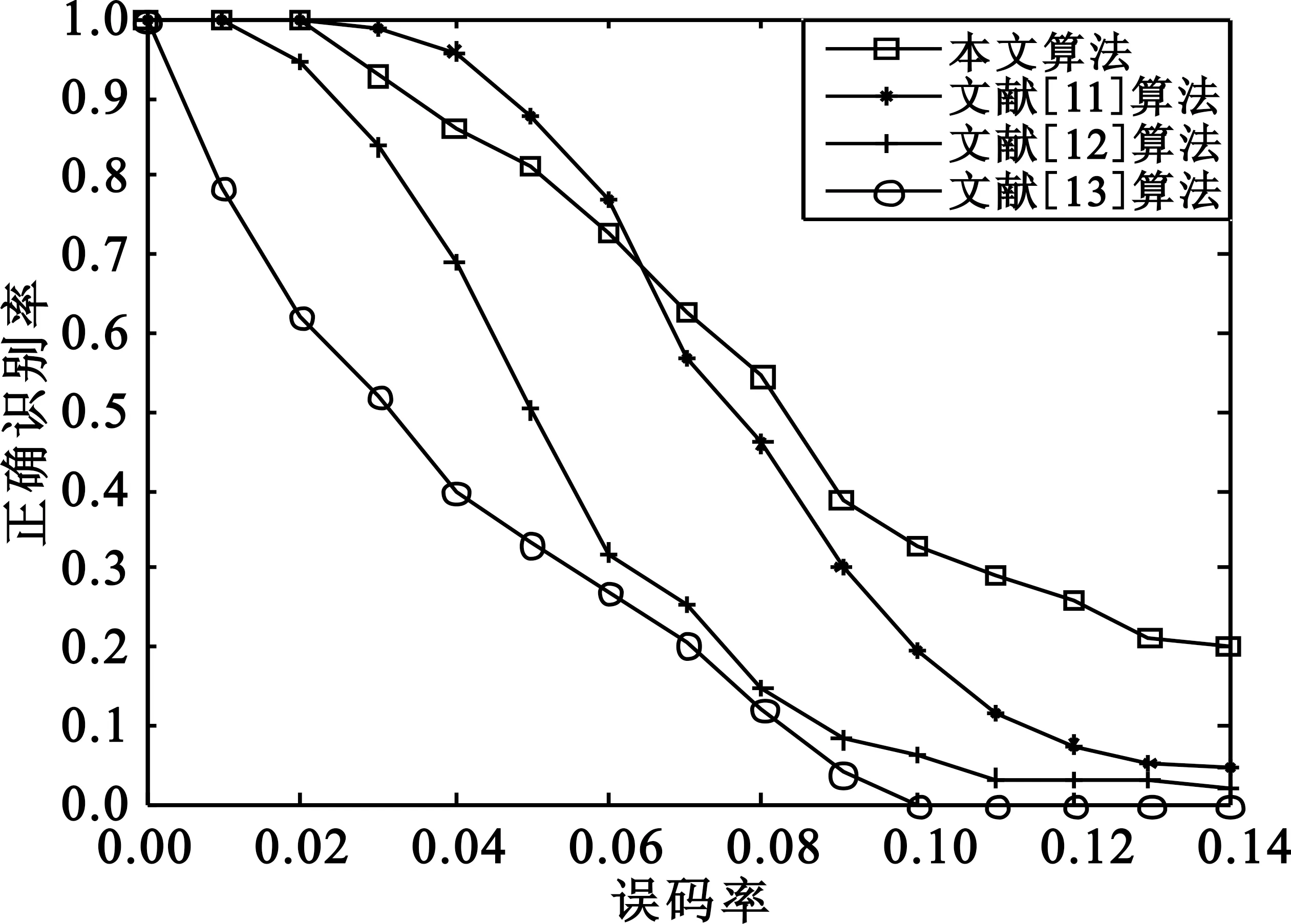
图10 不同算法性能对比Fig.10 Performance comparision among different algorithms
5 结 论
为抑制误码的扩散提出的基于分块矩阵变换的线性分组码盲识别方法,本文利用线性分组码相关列可以被化为0的特性,使用各列的列重来判断是否为相关列,再根据真实码长时相关列个数最大,成功识别码长和码字起始点。仿真实验证明,在和传统方法计算复杂度相当的情况下,有效抑制了误码的扩散,在高误码条件下依然可以有效识别码长和码字起点,而且与传统方法相比,本文方法提高了在高误码条件下的正确识别概率,显然有效抑制了误码的扩散。然而,如何进一步提升算法的容错性能是需要后续研究的难点。
[1] 王俊霞,张天骐,强幸子. 基于迭代列消元法的线性分组码参数盲识别[J].电讯技术,2017,57(2):197-202.
WANG Junxia,ZHANG Tianqi,QIANG Xingxi. Blind recognition of linear block codes parameters based on iterative column elimination algorithm[J].Telecommunication Engineering,2017,57(2):197-202.(in Chinese)
[2] MARAZIN M,GAUTIER R,BUREL G. Dual code method for blind identification of convolutional encoder for cognitive radio receiver design[C]//Proceedings of 2009 Global Telecommunications Conference.Hawaii,USA:IEEE,2009:1-6.
[3] MARAZIN M,GAUTIER R,BUREL G. Algebraic method for blind recovery of punctured convolutional encoders from an erroneous bitstream[J].IET Signal Processing,2012,6(2):122-131.
[4] BUREL G,GAUTIER R. Blind estimation of encoder and interleaver characteristics in a non cooperative context[C]//Proceedings of the Second IASTED International Coference on Communications,Internet and Information Technology.Scottsdale,AZ,USA:IEEE,2003:75-280.
[5] 闫郁翰,汤建龙. 基于汉明距离的二进制线性分组码盲识别方法[J].通信对抗,2011(4):20-23.
YAN Yuhan,TANG Jianlong. Blind recognition method of binary linear block codes based on hamming distance[J].Communication Countermeasures,2011(4):20-23.(in Chinese)
[6] 王兰勋,李丹芳,汪洋. 二进制本原BCH码的参数盲识别[J].河北大学学报(自然科学版),2012,32(4):416-420.
WANG Lanxun,LI Danfang,WANG Yang. Blind recognition of binary primitive BCH codes parameters[J].Journal of Hebei University(Natural Science Edition),2012,32(4):416-420.(in Chinese)
[7] 杨晓静,闻年成. 基于码根信息差熵和码根统计的BCH码识别方法[J].探测与控制学报,2010,32(3):69-73.
YANG Xiaojing,WEN Niancheng. Recognition method of BCH codes based on roots information dispersion entropy and roots statistic[J].Journal of Detection and Control,2010,32(3):69-73.(in Chinese)
[8] 吕喜在,黄芝平,苏绍璟. BCH码生成多项式快速识别方法[J].西安电子科技大学学报(自然科学版),2011,38(6):159-162.
LYU Xizai,HUANG Zhiping,SU Shaojing. Fast recognition method for generator polynomial of BCH codes[J].Journal of Xidian University(Natural Science Edition),2011,38(6):159-162.(in Chinese)
[9] LIN S,COSTELLO D J.Error control coding[M].2nd ed. New Jersey,USA:Prentice Hall,2005:44-45.
[10] CHABOT C. Recognition of a code in a noisy environment[C]//Proceedings of 2007 International Symposium on Information Theory.Nice,France:IEEE,2007:2211-2215.
[11] 张天骐,易琛,张刚. 基于高斯列消元法的线性分组码参数盲识别[J].系统工程与电子技术,2013,35(7):1514-1519.
ZHANG Tianqi,YI Chen,ZHANG Gang. Blind identification of parameters of linear block codes based on columns Gaussian elimation[J].Systems Engineering and Electronics,2013,35(7):1514-1519.(in Chinese)
[12] 张永光,楼才义,王挺.一种线性分组码编码参数的盲识别方法:201010131103.3[P].2010-10-13.
[13] 张旻,李歆昊. 基于关联规则的二进制线性分组码盲识别[J].系统工程与电子技术,2014,36(5):979-984.
ZHANG Min,LI Xinhao. Binary linear block code blind recognition based on association rules[J].Systems Engineering and Electronics,2014,36(5):979-984.(in Chinese)
BlindRecognitionofLinearBlockCodesBasedonBlockMatrixTransformation
ZHAO Liang,ZHANG Tianqi,YANG Qiang
(Chongqing Key Laboratory of Signal and Information Processing,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
To solove the problem of error diffusion in traditional matrix analysis methods,a linear block code blind recognition method is proposed based on block matrix transformation. Firstly,the analysis matrix is constructed according to the estimated code length,and the matrix is transformed into the low triangular matrix after the analysis matrix is divided. Then,the thresholds of the relevant columns are set according to the statistical distribution characteristics of the relevant column weights,and the number of correlation columns corresponding to the thresholds is counted when the number of related columns is the largest. The method is simple and can also identify codeword synchronization points. Theoretical analysis and simulation results show that the fault recognition performance of the method is good,and the correct recognition rate of(15,7) linear block codes can reach 80% under the condition of bit error rate of 5%.
linear block codes;blind recognition;block matrix transformation;related columns
date:2017-01-04;Revised date:2017-04-10
国家自然科学基金资助项目(61671095,61371164);信号与信息处理重庆市市重点实验室建设项目(CSTC2009CA2003);重庆市教育委员会科研项目(KJ130524,KJ1600427,KJ1600429)
**通信作者:535836848@qq.com Corresponding author:535836848@qq.com
TN911.22
A
1001-893X(2017)10-1107-07

赵亮(1991—),男,河南洛阳人,硕士研究生,主要研究方向为信道编码参数的盲识别;
Email:535836848@qq.com
张天骐(1971—),男,四川眉山人,博士(后),教授,主要研究方向为语音信号处理、通信信号的调制解调、盲处理、神经网络实现以及FPGA、VLSI实现;
杨强(1991—),男,四川岳池人,硕士研究生,主要研究方向为通信信号处理。
10.3969/j.issn.1001-893x.2017.10.002
赵亮,张天骐,杨强.基于分块矩阵变换的线性分组码盲识别[J].电讯技术,2017,57(10):1107-1113.[ZHAO Liang,ZHANG Tianqi,YANG Qiang.Blind recognition of linear block codes based on block matrix transformation[J].Telecommunication Engineering,2017,57(10):1107-1113.]
2017-01-04;
2017-04-10

