基于最长公共子序列的非同步相似轨迹判断*
(中国西南电子技术研究所,成都 610036)
基于最长公共子序列的非同步相似轨迹判断*
刘 宇,王前东**
(中国西南电子技术研究所,成都 610036)
针对非同步相似轨迹判断问题,提出了一种基于最长公共子序列理论的相似轨迹判断新算法。首先,求出查询轨迹线段与候选轨迹线段之间的距离;其次,利用最长公共子序列算法,计算两轨迹的最长公共子轨迹长度;最后,根据相似度门限,判断轨迹是否相似。数值实例验证了所提算法能够提高非同步轨迹的相似度。
侦察监视;最长公共子序列;非同步相似轨迹;最长公共子轨迹
1 引 言
近年来,目标的行为活动规律备受关注。在目标侦察监视系统中,目标经常在某个区域进行着相似的侦察行动,这使得目标的运动轨迹具有较强的相似性。通过对获取的目标的轨迹进行分析、理解并判断目标的行为活动规律是侦察监视系统的重要任务之一。
对于目标轨迹的分析,关键是轨迹间相似性的判断。轨迹间的相似性判断可以通过轨迹间的距离来表示。现有的轨迹距离表示方法主要有欧式距离(Euclidean)、动态时间弯曲距离(Dynamic Time Warping,DTW)[1]、最长公共子序列[2-14](Longest Common Subsequence,LCS)等。欧式距离法使用较早、计算简单,但要求所有的轨迹不能有强噪声,而且所有的轨迹必须有相同的点数。动态时间弯曲距离法对所有的轨迹不再要求有相同的点数,但要求所有的轨迹不能有强噪声。最长公共子序列法对所有的轨迹不再要求有相同的点数,能处理具有少量强噪声的轨迹,即最长公共子序列方法既能处理不同点数的轨迹,又能处理具有强噪声的轨迹,已成为轨迹相似判断的重要方法之一。
文献[3]将轨迹看作序列,将相似轨迹问题转化为最长公共子序列问题,提供了一个基于最长公共子序列算法的相似度量,用实验证明了该度量既能处理不同点数的轨迹,又能处理具有强噪声的轨迹,比常用的欧式距离和动态时间弯曲距离鲁棒,但该文没有处理轨迹不同步的情形。
在实际中,获取的目标轨迹起点不同,采样周期也不同,因此目标轨迹是不同步的。本文利用文献[3]的思想,针对这种非同步的轨迹,将轨迹之间点与点的比较转化为轨迹之间线段与线段的比较,提出一种基于最长公共子序列的相似轨迹判断新算法。
2 相似轨迹基础知识
2.1最长公共子序列
设两序列Qm=(q1,q2,…,qm)与Cn=(c1,c2,…,cn)的公共子序列为Zr=(z1,z2,…,zr),则Zr必须满足
(1)
Zr为两序列Qm与序列Cn的最长公共子序列,当且仅当Zr为满足上述条件中最长的公共子序列。
令L(m,n)表示序列Qm与序列Cn的最长公共子序列长度,则L(m,n)有如下递推计算公式:
(2)
L(m,n)为一般的最长公共子序列算法,其推导见参见文献[1]。L(m,n)计算的时空复杂度为O(mn)。
2.2基于最长公共子序列的相似轨迹
设有轨迹Qm=((qx,1,qy,1),…,(qx,m,qy,m))与轨迹Cn=((cx,1,cy,1),…,(cx,n,cy,n)),则有如下定义:
定义1 令ε>0为距离阈值,令L1ε(m,n)为轨迹Qm与轨迹Cn按点迹距离定义的最长公共子轨迹长度,则L1ε(m,n)可由如下递推公式求出:
(3)
其中:dis(qi,cj)为两点qi与cj的欧式距离。计算L1的初始值为:对任意i≥0,L1ε(i,0)=0;对任意j≥0,L1ε(0,j)=0。
根据公式(3)求出的L1ε(m,n)即为L1ε(Qm,Cn)。
定义2 令ε>0为距离阈值,令f1为轨迹Qm与轨迹Cn按点迹距离定义的相似度,则f1可由如下公式求出:

(4)
定义3 令λ>0为相似度阈值,则轨迹Cn与轨迹Qm按点迹距离相似轨迹当且仅当:
f1ε(Qm,Cn)≥λ。
(5)
例1:基于最长公共轨迹的相似轨迹判断
设有如下3个轨迹序列:查询轨迹Q={10,20,30,40,50,60,70,80,90,100}及两候选轨迹C1={1,11,21,31,41,51,61,71,81,91,101}和C2={5,15,25,35,45,55,65,75,85,95,105}。
令距离阈值为ε=2,λ=0.5,则轨迹Q与C1的相似度f1ε(Q,C1)= 100%>λ,两轨迹Q与C1相似;轨迹Q与C2的相似度f1ε(Q,C2)=0<λ,两轨迹Q与C2不相似。这两轨迹Q与C2判为不相似与实际不符。实际上,Q与C2明显是同一轨迹,只是采样点时间不同步造成了轨迹数值有差异。
3 非同步相似轨迹判断新算法
设有轨迹Qm=((qx,1,qy,1),…,(qx,m,qy,m))与轨迹Cn=((cx,1,cy,1),…,(cx,n,cy,n)),则有如下定义:
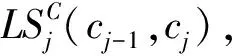
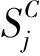
(6)
其中:dis(qi,c)为两点qi与c的欧式距离。

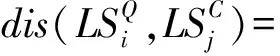

(7)
定义6 令ε>0为距离阈值,令L2ε(Qm,Cn)为轨迹Qm与轨迹Cn按线段距离定义的最长公共子轨迹长度,则L2ε(Qm,Cn)可由如下递推公式求出:
(8)
其中:计算L2的初始值为L2ε(i,1)=0或L2ε(1,j)=0,i=2,3,…,m;j=2,3,…,n。
根据公式(8)求出的L2ε(m,n)即为L2ε(Qm,Cn)。
定义7 令f2为轨迹Qm与轨迹Cn按线段距离定义的相似度,则f2可由如下公式求出:
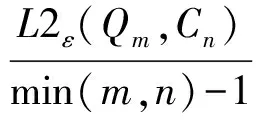
(9)
定义8 令λ>0为相似度阈值,则轨迹Cn与轨迹Qm按线段距离相似当且仅当
f2ε(Qm,Cn)≥λ。
(10)
根据以上定义,有如下的非同步轨迹相似判断的计算流程:
Step1 用0初始化长度为m、n的公共轨迹长度矩阵L(m,n)。
Step2 利用公式(8),通过两重循环算法计算两轨迹的公共轨迹长度矩阵L(m,n),L(m,n)即为Qm与Cn的最长公共轨迹长度L2ε(Qm,Cn):
Fori=2:m
Forj=2:n

L(i,j)=L(i-1,j-1)+1;
Else
L(i,j)=max(L(i-1,j),L(i,j-1));
End
End
End
Step3 根据公式(9)计算两轨迹的相似度f2ε(Qm,Cn)。
Step4 根据公式(10)和设定的阈值λ判断两轨迹是否相似。
根据以上的计算流程可以看出有如下两个定理成立:
定理1 令ε>0为距离阈值,计算轨迹Qm与轨迹Cn的最长公共子轨迹长度L2ε(Qm,Cn)的时间复杂度为O(mn),其中m、n分别为查询轨迹Qm、候选轨迹Cn的轨迹长度。
证明:从计算流程中可以看出,Step1,初始化矩阵L的时间复杂度为O(mn);Step2,为计算L(m,n)的关于m、n的两重循环,其时间复杂度为O(mn);Step3与Step4的时间复杂度为O(1)。故计算L2ε(Qm,Cn)的时间复杂度为O(mn)。
定理2 令ε>0为距离阈值,f1和f2分别为轨迹Qm与轨迹Cn按点迹距离和按线段距离定义的相似度,则有f2≥f1。
证明:由点迹距离与线段距离定义可有如下结论成立:
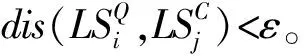
利用此结论,由最长公共子序列递推公式(3)和公式(8)可推出如下结论成立:
L1ε(m,n)≤L2ε(m,n)+1 。
(11)
由此即可推出如下结论成立:

(12)
两序列的最长公共子序列长度肯定小于等于两序列长度定义,即
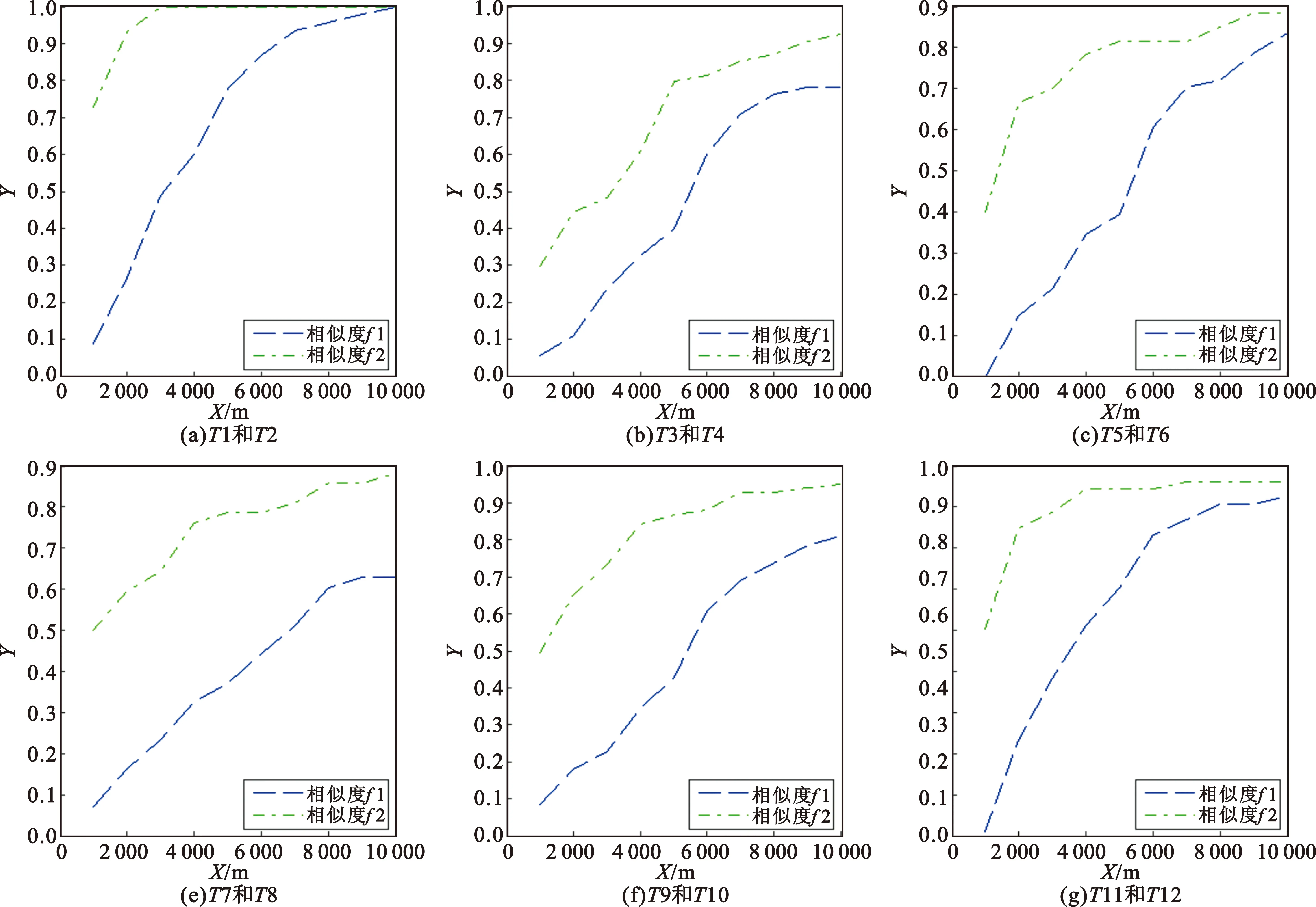
L2ε(m,n) (13) 由公式(12)和公式(13),有 (14) 利用此不等式,由相似度定义可推出f1ε(Qm,Cn)≤f2ε(Qm,Cn)。 例2:改进的相似轨迹判断 设有3个轨迹序列:查询轨迹Q={(0,1 000),(1 000,2 000),(2 000,4 000),(3 000,6 000),(4 000,9 000),(5 000,8 000),(6 000,6 000),(7 000,3 000),(8 000,4 000),(9 000,6 000)}m及两候选轨迹C1={(0,1 001),(1 000,2 001),(2 000,4 001),(3 000,6 001),(4 000,9 001),(5 000,8 001),(6 000,6 001),(7 000,3 001),(8 000,4 001),(9 000,6 001)}m和C2={(500,1 500),(1 500,3 000),(2 500,5 000),(3 500,7 500),(4 000,9 000),(4 500,8 500),(5 500,7 000),(6 500,4 500),(7 000,3 000),(7 500,3 500),(8 500,5 000)}m。其中轨迹Q与轨迹C1是同步轨迹(点数和周期都相同),每点位置距离只差1 m,如图1中的同步轨迹所示;轨迹C2与轨迹Q是异步轨迹(点数和起点都不相同),除了C2中的第5点(4 000,9 000)m和第9点(7 000,3 000)m分别与Q中的第5点和第8点相同外,轨迹C2中其他点与轨迹Q的点之间的距离至少相差500 m,如图1中的异步轨迹所示。 图1 同步与异步轨迹图Fig.1 Synchronous track and asynchronous track 令距离阈值为ε=2,λ=0.5,则按文献[3]的方法计算的轨迹Q与C1的最长公共轨迹长度为10,轨迹Q与C1的相似度f1ε(Q,C1)= 100%,两轨迹Q与C1判为相似;轨迹Q与C2只有两点接近,轨迹Q与C2的最长公共轨迹的长度为2,轨迹Q与C2的相似度f1ε(Q,C2)=20%,两轨迹Q与C2判为不相似。 同样令距离阈值为ε=2,λ=0.5,按本文新方法计算的轨迹Q与C1的公共轨迹的长度为9,轨迹Q与C1的相似度f2ε(Q,C1)= 100%,两轨迹Q与C1判为相似;轨迹Q与C2的公共轨迹长度为9,轨迹Q与C2的相似度f2ε(Q,C2)=100%,两轨迹Q与C2判为相似。 从上面的例子看出,本文的新方法既可以用于同步轨迹(Q与C1)的判断,又可以用于非同步轨迹(Q与C2)的判断。 在某次仿真实验中,仿真了12个目标的6组典型轨迹,6组轨迹几乎不同步(轨迹起始点和终止点不同,轨迹点数不同,轨迹采样周期不同)。6组12个目标的运动轨迹如图2所示。 图2 目标的运动轨迹图Fig.2 Motion track of targets 从图2中可以看出,12个目标组成的6组轨迹{T1,T2}、{T3,T4}、{T5,T6}、{T7,T8}、{T9,T10}、{T11,T12}几乎相同,故可用这6组数据进行轨迹相似性检验。 设距离阈值ε为1~10 km,则6组目标按点迹距离计算的相似度和按线段距离计算的相似度分别为f1和f2,如图3所示。 图3 不同距离门限阈值的相似度图Fig.3 Similarity measure for different distance gate 从图3可以看出,针对不同目标和不同距离门限阈值,本文提出的新方法计算的相似度f2都比文献[3]提出的相似度f1高,本文提出的方法更能适应非同步的相似轨迹的判断;随着门限值增大,本文提出的新方法计算的相似度f2逐渐逼近文献[3]提出的相似度f1。 本文利用线段距离,通过LCS算法改进轨迹相似度判断方法,使算法更适用于不同步轨迹之间的判断。数值实例表明,本文的改进方法更适用于非同步的轨迹判断中。数值仿真实验表明,本文计算的相似度f2比文献[3]计算的相似度f1高,本文算法能够提高非同步轨迹计算的相似度。 本文算法可以进一步应用于轨迹的聚类、轨迹的规律分析及轨迹的查询、识别等。在实际应用中,相似度的计算跟距离阈值ε有关,阈值的大小需要根据具体的应用要求修改。 [1] AGRAWAL R,FALOUTSOS C,SWAMI AN. Efficient similarity search in sequence databases[C]// Proceedings of International Conference on Foundations of Data Organization and Algorithms. Chicago:Springer-Verlag,1993:69-84. [2] LI Q,SUN M. On discovery of learned paths from taxi origin-destination trajectories[C]// Proceedings of 2015 34th Chinese Control Conference (CCC).Hangzhou:IEEE,2015:3896-3901. [3] VLACHOS M,GUNOPOULOS D,KOLLIOS G. Discovering similar multidimensional trajectories[C]// Proceedings of International Conference on Data Engineering. San Jose:IEEE Computer Society,2002:673. [4] PELEKIS N,KOPANAKIS I,MARKETOS G,et al. Similarity search in trajectory databases[C]// Proceedings of International Symposium on Temporal Representation and Reasoning. Alicante:IEEE,2007:129-140. [5] SKOUMAS G,SKOUTAS D,VLACHAKI A. Efficient identification and approximation of k-nearest moving neighbors[C]//Proceedings of ACM Sigspatial International Conference on Advances in Geographic Information Systems. New York:ACM,2013:264-273. [6] YUAN Y H,RAUBAL M. Measuring similarity of mobile phone user trajectories-a spatio-temporal edit distance method[J].International Journal of Geographical Information Science,2014,28(3):496-520. [7] YING J C,LU H C,LEE W C,et al. Mining user similarity from semantic trajectories[C]//Proceedings of ACM Sigspatial International Workshop on Location Based Social Networks. San Jose:ACM,2010:19-26. [8] WANG H,LIU K. User oriented trajectory similarity search[C]//Proceedings of ACM SIGKDD International Workshop on Urban Computing. Beijing: ACM, 2012:103-110. [9] WANG H,ZHONG J,ZHANG D. A duplicate code checking algorithm for the programming experiment[C]//Proceedings of Second International Conference on Mathematics and Computers in Sciences and in Industry. Sliema:IEEE,2016:39-42. [10] REKABDAR B,NICOLESCU M,NICOLESCU M,et al. Scale and translation invariant learning of spatio-temporal patterns using longest common subsequences and spiking neural networks[C]//Proceedings of International Joint Conference on Neural Networks. Killarney:IEEE,2015:1-7. [11] GU Y,CHEN M,REN F,et al. HED:handling environmental dynamics in indoor wifi fingerprint localization[C]//Proceedings of Wireless Communications and NETWORKING Conference. Doha,IEEE,2016:1-6. [12] HO S S,DAI P,RUDZICZ F. Manifold learning for multivariate variable-length sequences with an application to similarity search.[J].IEEE Transactions on Neural Networks & Learning Systems,2015,27(6):1333-1344. [13] BEAL R,AFRIN T,FARHEEN A,et al. A new algorithm for the LCS problem with application in compressing genome resequencing data[C]//Proceedings of IEEE International Conference on Bioinformatics and Biomedicine. Washington DC:IEEE,2015:69-74. [14] PROZOROV D,YASHINA A. The extended longest common substring algorithm for spoken document retrieval[C]//Proceedings of International Conference on Application of Information and Communication Technologies. Rostov-on-Don,Russia:IEEE,2015:88-90. ComputingSimilarMeasurebetweenTwoAsynchronousTrajectoriesBasedonLongestCommonSubsequenceMethod LIU Yu,WANG Qiandong For the problem of judging the asynchronous similar trajectory,a new algorithm for computing the similar trajectories is proposed based on the Longest Common Subsequence (LCS) method. Firstly,the line segment distances,which are between line segments of the query trajectory and the line segments of the candidate trajectory,are computed by the line segment distance. Secondly,the length of the longest common sub-trajectory,which is between the query trajectory and the candidate trajectory,is computed by the LCS method. Finally,the similarity measure between two trajectories is computed and the similar trajectory is got. Simulation shows the new method can improve the similarity measure between two asynchronous trajectories. reconnaissance and surveillance;longest common subsequence;asynchronous similar trajectory;longest common sub-trajectory date:2017-04-01;Revised date:2017-08-23 **通信作者:wangqiandong@sohu.com Corresponding author:wangqiandong@sohu.com TN957.52 A 1001-893X(2017)10-1165-06 刘宇(1977—),男,四川广汉人,2000年于四川大学获学士学位,现为工程师,主要研究方向为情报侦察及情报处理; 王前东(1977—),男,四川西充人,2004年获硕士学位,现为高级工程师,主要从事情报数据融合处理研究。 Email:wangqiandong@sohu.com 10.3969/j.issn.1001-893x.2017.10.011 刘宇,王前东.基于最长公共子序列的非同步相似轨迹判断[J].电讯技术,2017,57(10):1165-1170.[LIU Yu,WANG Qiandong.Computing similar measure between two asynchronous trajectories based on longest common subsequence method[J].Telecommunication Engineering,2017,57(10):1165-1170.] 2017-04-01; 2017-08-23
4 数值实例

5 数值仿真试验

6 结 论
(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

