卫星导航中XFAST捕获的降计算量去模糊处理算法*
(北京信息科技大学 信息与通信工程学院,北京 100101)
卫星导航中XFAST捕获的降计算量去模糊处理算法*
赵盼盼,姚彦鑫**
(北京信息科技大学 信息与通信工程学院,北京 100101)
卫星导航系统中,采用扩展复制重叠法(Extended Replica Folding Acquisition Search Technique,XFAST)对长PN码进行直接捕获时,粗捕后得到的对齐码相位存在重叠模糊度。为减少去模糊处理的计算量,提高捕获速度,提出了一种新的去模糊处理算法。新算法在得到粗捕对齐码相位结果后,先对本地码序列重新按照对齐相位进行排列、分段、段内循环移位等操作,然后进行段间叠加,再与接收码序列通过FFT-IFFT运算实现循环相关运算,从而确定对齐码相位所在的子码段,得到无模糊度的捕获结果。理论分析与仿真结果证明,该算法可以在分段叠加段数和子段长满足一定关系的条件下,在检测性能满足系统要求下,大大降低去模糊处理的计算量和操作时间,从而提高捕获速度。
卫星导航系统;长码直捕;快速捕获;去模糊;计算量;折叠相关
1 引 言
GPS信号采用C/A码和P码两种不同的伪随机码。其中C/A码称为粗码,是一种低码率、周期重复的短码;P码称为精码,是一种高码率、长周期、加密的伪随机码[1]。传统的P码捕获一般采用C/A码引导的方式,但是C/A码码率低、容易受敌方干扰和欺骗,在强干扰和欺骗的战争环境中,辅助捕获很难实现。由于P码具有比C/A更强的反干扰和反欺骗的特性,因此要求在军事通信和导航系统中具备对P码快速直接捕获的能力。
因为P码具有6.1871×1012个码元[2],完成P码直接捕获需要很长的捕获时间和巨大的计算量。针对此问题,近年来国内外对于P码的直接捕获算法进行了大量的研究。按照捕获策略可分为串行、并行和混合型,按照处理域又可以分为时域和频域两种处理方式。由于串行搜索方法[3]是逐个检测码相位,导致搜索过程非常长,搜索效率低,不适用于大范围搜索。分块并行搜索码相位的混合型方法成为许多快速捕获P码方案的基础。
典型的P码直接捕获算法有补零法 (Zero-Padding Method,ZPM)[4]、扩展复制重叠法 ( Extended Replica Folding Acquisition Search Technique,XFAST)[5]、直接平均法 (Direct Average Method,DAM)[6]、重叠平均法 (Overlap Average Method,OAM)[7],以及在此基础上的各种演变算法[8-10]。其中XFAST由Yang等人[5]于1999年提出,其核心是通过将长度为M×N的本地码序列进行M段叠加,利用分段叠加码序列与长度为N的接收码序列进行循环相关运算,使伪码相位并行搜索范围扩大至(M-1)N+1个码相位。与其他方法相比,XFAST可以显著提高搜索效率。
文献[11-12]对XFAST算法性能及应用进行了广泛的讨论,但都是从算法参数方面进行优化。本文以解决XFAST粗捕后码相位存在重叠模糊度的问题为目标,提出了一种卫星导航中XFAST捕获的降计算量去模糊处理算法。与XFAST去模糊处理算法进行计算量和操作时间的对比分析,当本地码序列分段叠加段数和子段长度满足一定条件时,本文提出的去模糊算法使得计算量和操作时间明显降低,从而提高了去除模糊度的速度。文中还对新去模糊处理算法的检测性能进行了理论分析和仿真分析。
2 算法描述
2.1XFAST捕获算法
接收的基带信号可用以下公式表示:
sl=sI,l+jsQ,l(l=0,1,2,…) 。
(1)
式中:sI,l=Adl+λcl+λcos(2πfDlΔt+φ)+nI,l为同相分量,sQ,l=AdQ+λcQ+λsin(2πfDlΔt+φ)+nQ,l为正交分量,A为信号幅度,dl+λ∈{+1,-1}为导航电文,cl+λ∈{+1,-1}为调制扩频码,fD为多普勒频偏,Δt为采样间隔,φ为载波初始相位,l为采样索引,λ为接收信号的伪码相位,nI,l、nQ,l分别为同相和正交分量中的加性高斯白噪声。
接收信号采样序列s=sI+jsQ长度取N,其中sI=[sI,0,sI,1,…,sI,N-1]T为同相序列,sQ=[sQ,0,sQ,1,…,sQ,N-1]T为正交序列。接收机以标称伪码频率产生本地伪随机码,经采样后码序列为[cδ,c1+δ,c2+δ,…,cl+δ]T(l=0,1,2,…),δ为本地伪码相位。
XFAST算法是建立在被捕获伪码的优良自相关特性的基础之上,码的自相关性能越好,则处理效率越高;码周期越长,因分段叠加引起的干扰越小。XFAST算法的原理是,根据接收信号采样序列s=sI+jsQ的长度N,在本地伪码序列扩展M段的情况下,接收机产生长度为M×N的本地伪码序列[cδ,c1+δ,c2+δ,…,cMN-1+δ]T,将其分成M段长度为N的子码序列
rm=[cmN+δ,cmN+1+δ,…,cmN+N-1+δ]T,
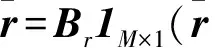

由于XFAST粗捕得到的码相位具有模糊度,即重叠模糊度,为了得到精确的伪码相位值,需要进行去除重叠模糊度处理,也可称为精捕。根据粗捕得到的对齐码相位,对本地码序列进行重新排列,方法为:根据粗捕得到的对齐码位置对本地码序列进行循环左移,移位位数为粗捕得到的对齐码位置值减1(例如:粗捕得到的对齐码位置值为3,则移位位数为2),从而以粗捕得到的对齐码中第一个原始码片为本地码序列的起点,即c1成为本地码序列的起点。将重新排列的本地码序列分成M段长为N的子码段序列,各个新子码序列分别与接收码序列在时域中进行线性相关运算,在得到的M个相关值中,最大值对应的子码段即为粗捕得到的码相位所在的子码段,如图1所示。
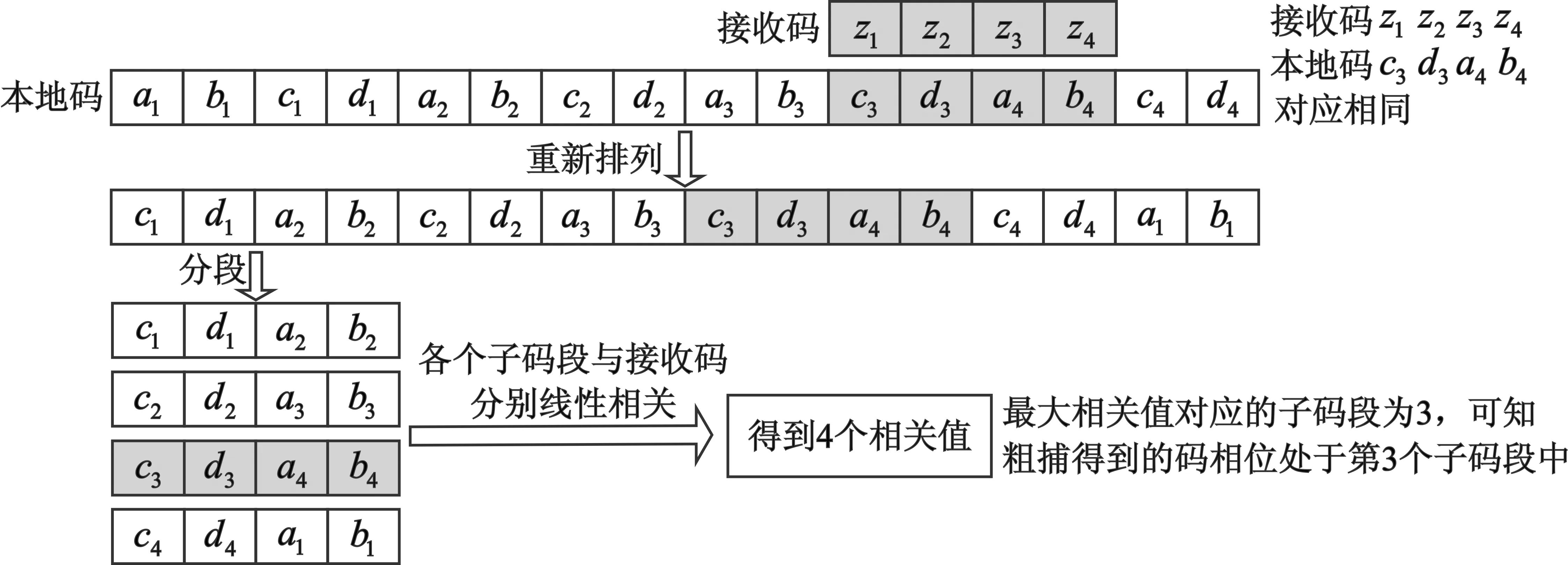
图1 XFAST去模糊算法(精捕)Fig.1 The algorithm of XFAST ambiguity resolution(fine capture)
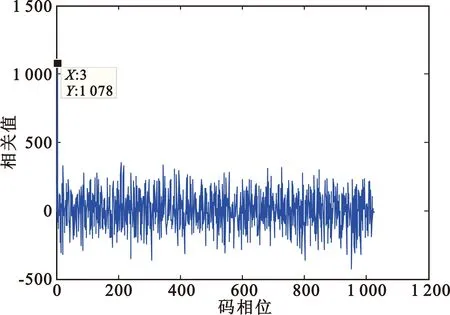
图1中最大相关值为接收码序列与第3段本地子码序列的相关值,即粗捕得到的码相位处于第3个子码段中。根据粗捕得到对齐码片位置3和去模糊处理得到的码相位所处的子码段3,可以计算得出接收码序列与本地码序列在第11(计算过程为3+(3-1)×4=11)个码片c3处对齐。
2.2新去模糊处理算法
本文提出的去模糊算法同样是利用P码具有优良的自相关性的特点,从而获得较高的处理效率。其步骤是对本地码序列重新排列、分段、段内循环移位后叠加,然后再与接收码序列通过FFT-IFFT运算实现循环相关运算,根据相关结果最大值确定粗捕得到的对齐码所在的具体子码段,如图2所示。

图2 新去模糊处理算法Fig.2 The new algorithm of ambiguity resolution
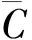
Step2 各个子码段序列分别循环右移,移位位数为相应的子码段号减1。例如:第1段循环右移0位,第2段循环右移1位,以此类推,第M段循环右移M-1位。
Step3 将移位后的各子码段序列对应相加,得到一个新的长为N的分段叠加码序列,对新的分段叠加码序列进行N点FFT运算。
Step4 将Step 3中的计算结果与接收码序列的FFT计算结果进行复共轭相乘。
Step5 将得到的结果进行N点IFFT运算,在得到的N个相关值中,最大值对应的本地码片位置序号即为粗捕得到的对齐码相位所在的本地子码段序号。
根据粗捕得到对齐码片位置和去模糊处理得到的码相位所处的子码段,可以计算得出接收码序列与本地码序列对应相同的唯一码相位。
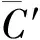
3 性能分析
3.1捕获概率和虚警概率
3.1.1XFAST新去模糊算法捕获概率分析
新去模糊算法与XFAST粗捕算法的唯一不同之处在于,新去模糊算法对重新分段的本地子码段序列进行了循环移位。根据P码优良的自相关特性,码对齐出现的相关峰值位置跟随对齐码循环移位而相应地移位,而对于峰值大小没有影响,同样对于码未完全对齐产生的互相关噪声也没有影响。因此,移位前、后的子码段序列与接收码序列进行循环相关的两种结果,对峰值的检测性能是相同的。此处用非移位子码段的叠加码序列与接收码序列的循环相关结果进行检测性能分析。
接收码序列与本地分段叠加码序列进行相关运算,相关结果包括同相相关和正交相关两部分,对同相相关结果CI进行详细分析,正交相关结果CQ与之类似。同相相关结果表达式如下:

(2)
同相相关结果CI由3项构成:相干积分、自噪声和加性高斯白噪声。假设接收信号的同相采样序列sI与本地码序列有n(n=0,1,…,N)个码元对应相同,接收信号同相采样序列的sI,g~sI,g+n-1与本地码序列的ch+δ~ch+δ+n-1对应相同,g、h分别为接收码序列和本地码序列对应相同码段的首个码相位的索引,则相干积分项为
(3)
其中:φ1=2πfDΔtg+φ。在相干积分过程中,认为导航电文为常数dλ。n=0说明不存在相干积分项,n=N说明本地信号包含所有的接收信号。ΩI的均值为
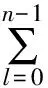
(4)
其中:p=[(g+λ)-(h+δ)]-⎣(g+λ)-(h+δ)」为残余码相位偏移(⎣y」表示不大于y的最大整数)。假设H0表示被检测信号不存在,即接收信号只含有噪声,则R0(p)=0;H1表示被检测信号存在,即接收信号中同时含有信号和噪声,则R1(p)=1-|p|。由于ΩI的方差不大于A2nGi(p),近似认为ΩI的方差为A2nGi(p),其中G1(p)=p2,G0(p)=(1-|p|)2。根据中心极限定理,相干积分项近似服从高斯分布,即ΩI~ψ(EΩI,nA2Gi(p))。
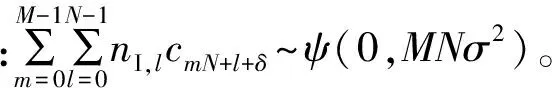
CI~ψ(EΩI,MN(σ2+A2)+nGi(p)A2-nA2),i=0,1。
(5)
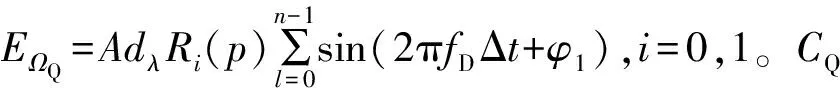
CQ~ψ(EΩQ,MN(σ2+A2)+nGi(p)A2-nA2),i=0,1。
(6)

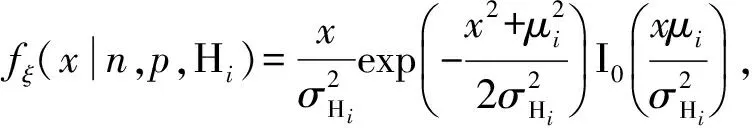
(7)
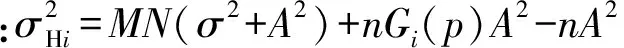
当接收信号中没有被检测信号时,令μi=0,得到fξ(x|0,p,H0)服从瑞利(Rayleigh)分布。概率密度函数
(8)
从而,虚警概率为
(9)
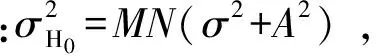
(10)
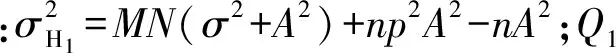
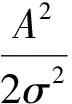
(11)
3.1.2XFAST的两种去模糊算法捕获概率对比
XFAST去模糊度算法将重新排列的各个新子码序列分别与接收码序列在时域中进行线性相关运算,同向相关结果表达式为
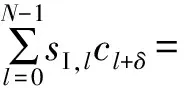
(12)

(13)
3.2计算量分析
3.2.1XFAST去模糊算法计算量
根据XFAST去模糊算法,将重新分段的各个本地子码段序列与接收码序列在时域中分别进行线性相关,共进行M次。每次相关运算乘法计算量为N,加法计算量为N-1,则总的乘法计算量为M×N,总的加法计算量为M×(N-1)。
3.2.2新去模糊算法计算量
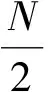
3.2.3计算量对比分析
相对来说,乘法计算量比加法计算量大很多,因此只考虑乘法的计算量。XFAST去模糊算法的乘法计算量为M×N,新去模糊算法的乘法计算量为NlbN+N。对两种去模糊算法的乘法计算量进行比较,当满足
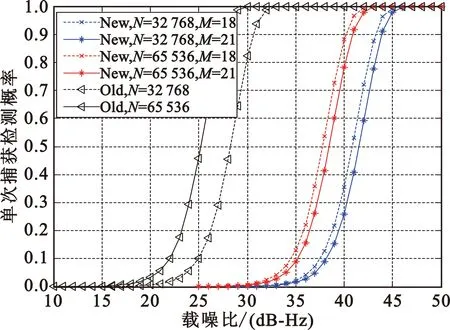
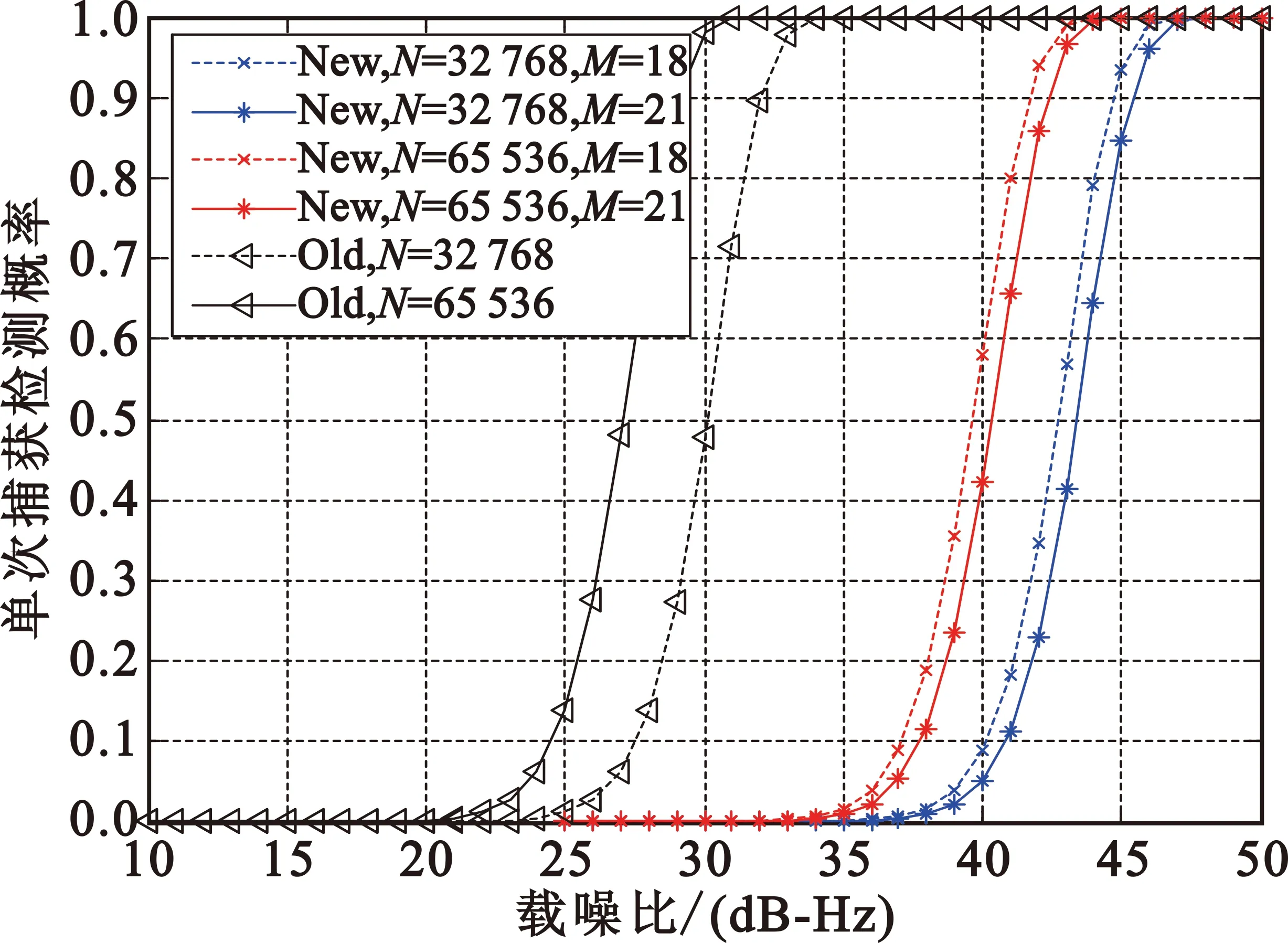
NlbN+N (14) 即N<2M-1时,本文提出的新去模糊算法比XFAST去模糊算法计算量小,相应地加快了去模糊处理的速度。当满足上述条件时,新去模糊算法相对于XFAST去模糊算法的计算量降低百分比为 (15) 其中:M为本地码序列分段叠加的段数,N为接收码序列长度。 3.3捕获时间分析 T1=(3lbN+2)t1。 (16) XFAST去模糊算法的乘法计算量为M×N,则完成一次XFAST去模糊处理算法需要的时间为 T2=2Mt1。 (17) 新去模糊算法的乘法计算量为NlbN+N,则完成一次新去模糊处理算法需要的时间为 T3=2(lbN+1)t1。 (18) 若用XFAST去模糊算法,则一次完整的P码捕获消耗的时间为 T4=T1+T2=(3lbN+2+2M)t1。 (19) 若采用新去模糊算法,则一次完整P码捕获消耗的时间为 T5=T1+T3=(5lbN+4)t1。 (20) 根据公式(19)可知,当接收码序列长度N一定时,新算法的捕获时间不随本地码序列叠加段数M变化;当本地码序列长度M×N一定时,本地码叠加段数M减小,随之选取的接收码序列长度N增大,则捕获时间随之变长,反之,捕获时间变短。 对两种去模糊算法的耗时进行对比分析,当满足T2>T3即N<2M-1时,本文提出的新去模糊算法比XFAST去模糊算法耗时短,相应地加快了去模糊处理的速度。当满足N<2M-1时,新去模糊算法相对于XFAST去模糊算法的消耗时间降低百分比为 (21) 4.1功能仿真 在Windows平台下,通过Matlab对本文提出的新去模糊算法进行功能仿真。此部分是说明新算法可以完成去模糊处理,暂时不考虑子码段序列长度和段数对性能方面的影响,选取了一组较短数据进行仿真说明。假设接收码长N为1 024;本地码总长16 384,分段叠加段数M为16,每段长度N为1 024;接收码序列与本地码序列中的第2 109~3 132的码片对应相同。图3中(a)为粗捕仿真图,(b)为新去模糊算法仿真图。 (a)XFAST粗捕 (b)新去模糊算法图3 XFAST粗捕和新去模糊算法Fig.3 XFAST coarse acquisition & new algorithm of ambiguity resolution 观察以上仿真波形图,由XFAST粗捕得到的对齐码相位在本地分段叠加码序列的第61个码片处,去模糊处理得到对齐码相位在本地码的第3个子码段,从而可以计算得知接收码序列与本地码序列对齐的具体码相位在本地码序列的第2 109(即61+1 024×(3-1))个码片处,与仿真条件中的假设相同。仿真结果表明,本文提出的新的去模糊算法可以准确地确定对齐码相位所在的本地码子段。 4.2检测性能仿真 为了方便理论分析,假设残余码相位偏移p=0,多普勒频偏fD=0,接收码序列长度N分别取32 768和65 536,本地码序列分段叠加段数M分别取18和21。在给定虚警概率Pfa=10-5和Pfa=10-7情况下,单次捕获检测概率随接收信号载噪比C/N0的变化如图4所示。 对于XFAST去模糊算法,检测概率与本地码序列分段叠加段数无关,随着接收码序列长度增加,捕获概率提高;当接收码序列长度以及接收信号载噪比一定时,随着虚警概率变大,则捕获概率变高。 (a)虚警概率Pfa=10-5 (b)虚警概率Pfa=10-7图4 单次检测概率随C/N0变化Fig.4 The probability of single detection vs. C/N0 对于新去模糊处理算法,当本地码序列分段叠加段数和接收信号载噪比一定时,随着接收码序列长度增加,捕获概率提高;当接收码序列长度和接收信号载载噪比一定时,随着本地码分段叠加段数增加,捕获概率降低。当本地码序列分段叠加段数、接收码序列长度以及接收信号载噪比一定时,随着虚警概率变大,则捕获概率会变高,当然虚警概率不能设定过大,否则会使得捕获性能变差。 两种去模糊算法检测概率对比分析可知,新去模糊处理算法的检测性概率有所降低。 4.3计算量仿真 FFT运算的数据个数必须为2的整数次幂,从而如果将FFT运用到P码捕获过程中,数据长度最长可取65 536(即216)约6.4 ms的数据记录。根据以上分析,截取不同长度的P码数据进行计算量对比分析,参数均满足条件N<2M-1,结果如表1所示。 表1 不同长度P码数据使用不同分段数处理的结果Tab.1 The results of different lengths P-code data processed using a different number of segments 由表1中的数据分析得知,在捕获P码过程中,选取合适的参数满足N<2M-1时,新去模糊算法的计算量得到明显降低。 4.4捕获时间仿真 截取不同长度的P码数据进行操作时间对比分析,参数均满足条件N<2M-1,根据公式(21),分析结果如表2所示。 表2 不同长度P码数据使用不同分段数捕获时间降低分析Tab.2 The capture time reduction analysis with different lengths P-code data using a different number of segments 由表2中的数据分析得知,在捕获P码过程中,选取合适的参数满足N<2M-1时,新去模糊算法的捕获时间得到明显降低。 采用扩展复制重叠法(XFAST)对长码捕获后,得到的对齐码相位存在重叠模糊度,XFAST去模糊处理需要逐段进行线性相关运算,多次线性相关的计算量与子码段长度和段数都成正比,计算量是偏大的。为了提高去模糊处理的计算效率,本文提出了一种卫星导航中XFAST捕获的降计算量去模糊处理算法,通过对本地码序列进行重新排列、分段、段内循环移位后叠加,再与接收码通过FFT-IFFT运算实现循环相关,确定对齐码相位所在的具体子码段,实现去模糊处理。 文中从理论上分析、比较了新旧去模糊处理算法的计算量,并推导出当接收码序列长度N与本地码序列扩展分段叠加段数M满足公式(14)中的条件时,采用本文提出的算法进行去模糊处理计算量明显降低,并通过仿真数据进行了分析验证。类似地,对比分析新旧去模糊处理算法的操作时间,在满足降低计算量的条件下,新算法捕获时间大大降低。对XFAST新去模糊处理算法的检测性能进行了理论与仿真分析,得出新算法的检测概率有所降低,但是检测性能可以满足系统要求。下一步研究的工作是在此基础上找到提高算法检测概率的方法策略。 [1] ELLIOTT D K,CHRISTOPHER J H. Understanding GPS:principles and applications[M]. 2nd Ed. Boston:Artech House Inc.,2006. [2] TSUI J B. Fundamentals of global positioning system receivers a software approach[M]. 2nd Ed. New Jersey:Wiley Interscience,2005. [3] POLYDOROS A,WEBER C L. A unified approach to serial search spread-spectrum code acquisition-part I & II[J]. IEEE Transactions on Communication. 1984,32(5):542-560. [4] LI H,LU M Q,FENG Z M. Improved zero-padding method for rapid long PN-code acquisition[J]. IEEE Transactions on Signal Processing,2008,56(8):3795-3799. [5] YANG C,VASQUEZ J,CHAFFEE J. Fast direct P(Y)-code acquisition using XFAST[C]//Proceedings of ION GPS 1999. Nashville:ION,1999:317-324. [6] PANG J. Direct global positioning system P-code acquisition field programmable gate array prototyping[D]. OH,USA:Ohio University,2003. [7] CUI H,LIAN B W. Study of GPS P-code direct acquisition technique[C]// Proceedings of IEEE International Conference on Broadband Network and Multimedia Technology.Beijing:IEEE,2010:1111-1114. [8] LI H,CUI X W,LU M Q et al. Dual-folding based rapid search method for long PN-code acquisition[J]. IEEE Transactions on Antennas and Propagation,2008,12(7):5286-5296. [9] XU Y,XU L J,YUAN H,et al. Direct P-code acquisition algorithm based on bidirectional overlap technique[J]. Journal of Systems Engineering and Electronics,2014,25(4):538-546. [10] FENG W Q,XING X D,ZHAO Q,et al. Dual-channel method for fast long PN-code acquisition[J]. Communications China,2014,11(5):60-70. [11] 唐小妹,庞晶,黄仰博,等.XFAST长码直捕算法参数优化设计[J]. 中南大学学报(自然科学版),2014,45(4):1113-1118. TANG Xiaomei,PANG Jing,HUANG Yangbo,et al. Optimization of XFAST design[J]. Journal of Central South University (Science and Technology),2014,45(4):1113-1118. (in Chinese) [12] 唐小妹,雍少为,王飞雪. 存在伪码多普勒条件下的XFAST性能分析[J].通信学报,2010,31(8):54-59. TANG Xiaomei,YONG Shaowei,WANG Feixue. Performance of XFAST in the presence of code Doppler[J]. Journal on Communications,2010,31(8):54-59. (in Chinese) [13] 黄劲松,刘峻宁,刘成宝,等.GPS信号载噪比研究[J].武汉大学学报(信息科学版),2007,32(5):427-430. HUANG Jinsong,LIU Junning,LIU Chengbao,et al. On C/N0 of received GPS signal.[J]. Geomatics and Information Science of Wuhan University,2007,32(5):427-430. (in Chinese) AnAmbiguityResolvingAlgorithmforXFASTAcquisitionwithLessComputationalAmountinSatelliteNavigation ZHAO Panpan,YAO Yanxin In satellite navigation system,extended replica folding acquisition search technique (XFAST) is used to capture long PN-code directly,but the aligned code phase obtained after coarse acquisition has overlapped ambiguity. In order to reduce the computational amount of resolving ambiguity and to speed up acquisition process,a new method is proposed. Firstly,local code chips are arranged according to the coarsely captured aligned code phase,segmented and shifted circularly within separate segments,and then all new local code sub-segments are folded together. Further,the code and the new local folded code are performing circular correlation operations through FFT-IFFT,and the precise code sub-segment of the aligned code phase can be determined. Thus the ambiguity of coarse acquisition can be solved. Theoretical analysis and simulation results demonstrate that,under the condition that the number of sub-segments and the length of the sub-segment satisfy certain relations,the proposed algorithm can reduce the computational amount of resolving ambiguity and operating time to speed up acquisition process greatly with the detection performance meeting the system requirements. satellite navigation system;direct acquisition of long code;rapid acquisition;ambiguity resolution;computational amount;folded correlation 10.3969/j.issn.1001-893x.2017.10.017 赵盼盼,姚彦鑫.卫星导航中XFAST捕获的降计算量去模糊处理算法[J].电讯技术,2017,57(10):1205-1212.[ZHAO Panpan,YAO Yanxin.An ambiguity resolving algorithm for XFAST acquisition with less computational amount in satellite navigation[J].Telecommunication Engineering,2017,57(10):1205-1212.] 2017-03-13; 2017-07-14 Received date:2017-03-13;Revised date:2017-07-14 国家自然科学基金资助项目(61302073);北京市自然科学基金资助项目(4172012,Z160002);北京市教委面上项目(KM201711232010) **通信作者:yanxin_buaa@126.com Corresponding author:yanxin_buaa@126.com TN967.1 A 1001-893X(2017)10-1205-08 赵盼盼(1990—),男,河北沧州人,硕士研究生,主要研究方向为GNSS关键技术; Email:zhaopanp321@163.com 姚彦鑫(1982—),女,河北人,2009年于北京航空航天大学获博士学位,现为副教授,主要研究方向为无线通信与节能通信网络、压缩感知与智能信号处理。 Email:yanxin_buaa@126.com


4 仿真分析




5 结束语
(School of Information and Communication Engineering,Beijing Information Science and Technology University,Beijing 100101,China)

