基于Kronecker积的无线通信系统参量分离方法*
(南通大学 电子信息学院,江苏 南通 226019)
基于Kronecker积的无线通信系统参量分离方法*
袁红林**,江立伟
(南通大学 电子信息学院,江苏 南通 226019)
针对无线通信系统中发射机非线性与多径衰落信道问题,提出了一种根据接收无线信号联合估计无线设备功率放大器(PA)非线性与无线信道单位脉冲响应的方法。首先,根据通信帧训练符号及发射机非线性模型构造卷积矩阵;接着,采用一次最小二乘(LS),根据接收信号估计PA的非线性模型系数与实际发送符号;然后,再采用一次LS,得到无线信道的单位脉冲响应估计;两估计可迭代或直接加取平均进行积累。理论推导与实验结果显示,采用过采样技术,所提方法可应用于单载波或多载波通信,实现PA非线性与无线信道单位脉冲响应的有效分离。新方法在无线通信的物理层射频指纹认证与信号可靠传输中具有应用价值。
无线信道;功率放大器非线性;参数分离; Kronecker积;射频指纹识别;射频指纹认证
1 引 言
通信发射机的非线性与无线多径衰落信道影响无线通信信号的可靠传输。然而,它们也被作为射频指纹[1-5]用于无线网络设备的物理层安全增强。
无线通信设备大都具有功率放大器(Power Amplifier,PA)与数模转换器(Digital Analog Converter,DAC)等非线性器件,这些器件具有的非线性会引起通信频带的带内失真与带外频谱再生等。其中,带内失真对于数据传输、相关检测与信道均衡等具有很大影响,而带外频谱再生会引起邻道干扰等。因此,估计无线设备的非线性并进行补偿,有利于通信系统性能的提高。文献[6]讨论了信道非线性特征引起的各种失真特征,总结并分析了常用的信道线性化技术。文献[7]基于Hammerstein模型和维纳模型模拟非线性结构,提出了一个由Hammerstein模型和维纳模型构建的非线性信道传输系统模型,并推导了3种非线性信道的均衡方法。文献[8]提出了一种基于维纳模型的非线性信道接收端均衡方案。
无线设备的非线性特征被作为一种射频指纹应用于无线网络设备的物理层认证[9-12]。文献[9]基于模型法提取通信发射机的非线性特征进行了无线设备个体识别的研究。文献[10]提取信号的互信息熵作为非线性动力学特征用于无线网卡的识别。文献[11]提出了一种非线性射频指纹变换方法。然而,文献[9-10]都未考虑无线多径衰落信道对射频指纹稳定性的影响。文献[12]提出了一种消除多径信道影响的无线设备非线性估计方法,基于发射机非线性模型因子的估计进行无线设备的个体识别实验,取得了95%的正确识别率。
另一方面,无线网络物理层安全的主流技术正是利用无线信道的唯一性以及其具有的互易性来提供安全服务[13]。
因此,准确估计无线设备非线性与无线信道特征,对于通信系统的性能改善以及无线网络的物理层信息安全都具有重要作用。
与已有其他文献不同,本文提出了一种通过两次最小二乘估计对无线设备非线性与无线信道单位脉冲响应进行积累估计与分离的方法,可应用于无线通信系统的非线性信道均衡与无线网络的物理层射频指纹认证等。
2 系统模型
假设无线设备的非线性主要由PA产生,并假设无线设备与无线信道在短时内时不变,则系统的基带等效模型如图1所示。

图1 系统基带等效模型Fig.1 Equivalent baseband system model
图1中,d[n]为基带发送信号;x[n]为经过PA功率放大后的基带发送信号;h[n]为无线信道的单位脉冲响应;v[n]为加性高斯白噪声(Additive White Gaussian Noise,AWGN);r[n]为基带接收信号,满足
r[n]=h[n]*x[n]+v[n]。
(1)
式中:*表示卷积运算。
设PA满足记忆多项式(Memory Polynomial,MP)模型[14],则x[n]与d[n]满足
(2)
式中:p=1,3,…,P与m=0,1,…,M分别是模型的非线性阶数与记忆长度;bp,m是相应的多项式因子,并假设b1,0=1。当M=0时,式(2)为无记忆系统;当M≠0时,式(2)为有记忆系统。式(2)可写成矢量形式:
(3)
其中:dp,m(n)是由p与m枚举组合而成的d[n-m]|d[n-m]|p-1构成的列矢量,bp,m是由相应bp,m构成的列矢量。
3 方法推导
假设第i帧的发送符号个数为Lx,采样率与符号率相同,无线信道径数为Lh,则接收符号长度为Lr=Lx+Lh-1。仅考虑当发送符号全部进入信道时情况,式(1)的矩阵表示为

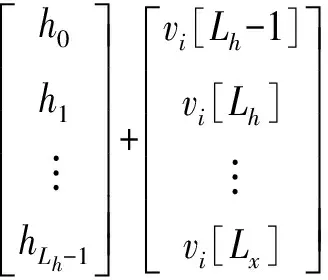
(4)
设ri=[ri[Lh-1],ri[Lh],…,ri[Lx]]T为接收信号矢量,h=[h0,h1,…,hLh-1]T为无线信道单位脉冲响应矢量,vi=[vi[Lh-1],vi[Lh],…,vi[Lx]]T为噪声信号矢量,则式(4)可表示为
ri=[xi(Lh-1)T,xi(Lh)T,…,xi(Lx)T]Th+vi。
(5)
式(5)中的行矢量
xi(m)=[xi[m],xi[m-1],…,xi[m-Lh+1]]∈1×Lh,
(6)
Lh-1≤m≤Lx。把式(3)代入式(6),则

(7)
其中:ILh为Lh×Lh的单位阵。把式(7)代入式(5)后得
ri=Di(h⊗bp,m)+vi。
(8)
式中:⊗为Kronecker积运算。
由于di[n]为先验的通信帧训练序列符号,因此根据式(8)可得h⊗bp,m的最小二乘(LS)估计为
(9)

进一步,根据式(2),可得经过PA后的发送符号估计为
(10)
根据式(5)与式(6),可得无线信道单位脉冲响应矢量的LS估计为
(11)

基于以上理论推导,可把不同帧的估计结果直接加取平均进行积累,或者进行迭代积累。一种迭代算法(PA非线性与无线信道脉冲响应的迭代积累分离算法)如下:
Step1 初始化:设置帧序号i=1,非线性因子估计和sumb=0,无线信道脉冲响应估计和sumh=0以及总帧数N。
Step2 初始估计:根据第1个通信帧的符号样值,构造dp,m,1与卷积矩阵D1。



Step6 重复。
Step7i←i+1。



Step12 后处理并输出。
算法的实质即基于不同帧的估计结果进行累加并取平均,只是迭代积累中利用了前次的无线信道单位脉冲响应估计。研究表明,两种积累方法的估计性能相近,具体见数值仿真实验。
4 数值仿真实验
为评估理论推导的正确性以及PA非线性与无线信道的联合估计性能,进行了基于加性高斯白噪声(AWGN)的数值仿真实验。
数值仿真实验分多载波OFDM及单载波通信两种场景进行。在OFDM通信场景下,分别对不同符号长度分离性能趋势以及有记忆与无记忆PA情况下的分离性能进行仿真;在单载波通信场景下,对算法分离与分类性能进行仿真。其中,4.2节与4.3节采用直接加取平均积累方法。
为衡量估计性能,定义bp,m与h的归一化均方误差(Normalized Mean Square Error,NMSE)为[15]

(12)
4.1OFDM下迭代积累算法的性能趋势
随机产生OFDM符号,根据接收信号进行一对发射机非线性与无线多径信道脉冲响应的迭代积累估计实验。
OFDM符号参数如下:16-QAM调制,符号长度Nfft为1 024、2 048或4 096,保护间隔Ng=Nfft/4,虚载波数Nvc=Nfft/4,循环前缀模式,OFDM符号个数Nvc为100或300。信噪比(Signal-to-Noise Ratio,SNR)设为10 dB,不同长度、不同个数OFDM符号时的NMSE如图2所示。

图2 10 dB 信噪比下不同长度/个数OFDM符号的NMSEFig.2 The NMSEs of the nonlinear coefficients and channel impulse response under 10 dB SNR environment with different length/number of OFDM symbols
图2显示,发射机的非线性因子与无线信道脉冲响应估计的NMSE随着积累OFDM符号个数的增加而呈降低趋势。然而,两估计的NMSE随着OFDM符号长度的变化而呈相反趋势,主要原因是迭代算法中信道脉冲响应的估计被用作除数估计非线性因子。
当SNR改变时,基于不同长度OFDM符号的估计NMSE如图3所示。

图3 不同长度OFDM符号随SNR变化的估计NMSEFig.3 The NMSEs of the nonlinear coefficients and channel impulse response versus SNR with different length of OFDM symbols
图3中,OFDM符号数为100,两个估计的NMSE随SNR的增加而线性降低,性能随OFDM符号长度变化的趋势没有改变。
4.2OFDM下PA有/无记忆场景
采用长度为160的IEEE 802.11 a/g[16]OFDM系统的长训练序列作为产生基带输入信号d[n]的基本单位(简称为1个header);对PA系数进行归一化,并对d[n]按照实验中所需的PA输出信号功率进行放大。
仿真采用PA为文献[17]中的Wiener Hammerstein (WH)模型,其结构如图4所示。

图4 仿真采用PA的WH模型结构
Fig.4 The structure of WH model of PA in simulations
图4中的H(z)、G(z)与A(ρ)、φ(ρ)分别为

(13a)

(13b)
(13c)
其中:式(13a)与式(13b)体现PA的记忆功能,而式(13c)体现PA的非线性;A(ρ)与φ(ρ)分别表示PA的归一化AM/AM与AM/PM特性;vA、ψA、vφ与ψφ分别为1、0.25、0.26与0.25。
假设无线信道的单位脉冲响应为h[n]=0.7δ[n]+0.3δ[n-1]+0.1δ[n-2]。仿真实验分PA的MP模型参数设定、无记忆与有记忆情况下MP模型多项式因子与无线信道脉冲响应估计性能三个方面进行。
4.2.1MP模型参数设定
首先进行参数为式(13)的WH模型PA的相应MP模型参数的设定与获取实验,MP模型参数包括阶数p、记忆深度m与多项式因子bp,m,分是否存在记忆两种情况进行。

无记忆MP模型的阶数与PA输出的NMSE之间关系如图5所示。

图5 无记忆MP模型输出NMSE与阶数之间关系Fig.5 The relationship between memoryless MP model output NMSE and orders
从图5可知,当P>7时,NMSE下降变缓,MP模型输出与WH模型实际输出之间差值约为NMSE=-15.7 dB,该无记忆PA的MP模型参数可以取P=7、M=0(泰勒级数),相应的奇数项因子见表1中设定值。

表1 无记忆MP模型PA的多项式因子Tab.1 The polynomial factors of the memoryless MP model
有记忆MP模型的阶数p、记忆深度m与PA输出的NMSE之间关系如图6所示。

图6 有记忆MP模型输出NMSE与阶数及记忆深度之间关系Fig.6 The relationship between memory MP model output NMSE and orders and memory depths
从图6可知,阶数越高,记忆深度越大,则MP模型越准确;但是多项式因子也越多,计算量也会急剧增多。当P=7且M=3时,NMSE=-19.99 dB,多项式奇数项因子个数为16。
4.2.2无记忆下MP模型因子与无线信道估计实验
基于上文中无记忆MP模型PA与无线信道参数进行仿真实验。帧训练序列长度分别为1~16个headers,不同SNR下的估计性能如图7所示。

图7 无记忆下MP模型因子与无线信道估计性能Fig.7 The estimation performance of factors of MP model without memory and wireless channel
如图7所示,随着SNR的增大,PA多项式因子与无线信道的NMSE都呈下降趋势;随着训练序列headers加倍,相应的NMSE基本下降3 dB,这与估计理论相符。
当SNR=30 dB、headers=16时,PA多项式因子的设定值与估计值如表1所示,相应的无线信道脉冲响应的设定值与估计值如表2所示。

表2 无线信道脉冲响应Tab.2 The impulse response of wireless channel
4.2.3有记忆下MP模型因子与无线信道估计实验
当P=7且M=3时,MP模型PA多项式因子与无线信道的估计实验结果如图8所示。

图8 有记忆下MP模型因子与无线信道估计性能Fig.8 The estimation performance of factors of MP model with memory and wireless channel
与图7相比,图8所示性能明显下降,原因是由于待估计的多项式因子数明显增多等。另外,图8中,随着帧训练序列的headers数加倍,NMSE不再呈现下降3 dB趋势,部分原因是由于LS估计时式(9)卷积矩阵不满秩与条件数不满足等。
4.3单载波通信场景
单载波通信场景下的仿真实验分两部分进行:首先,基于一对无线设备与相应的无线信道,进行发射机PA非线性模型系数与无线信道单位脉冲响应的分离实验;然后,采用基本的k-NN分类器,基于分离参数组合而成的特征矢量,进行两对无线设备与相应无线信道的分类实验。
数值仿真的实验场景如图9所示。

图9 数值仿真实验场景Fig.9 Experimental scene for numerical simulation
图9中,两个不同的无线设备用Transmitter-1与Transmitter-2表示,Channel-1、Channel-2分别为Transmitter-1、Transmitter-2与接收机之间的无线信道。两个无线设备的发射机PA非线性模型系数如表3所示。

表3 无线设备发射机PA的非线性模型系数Tab.3 The coefficients of the nonlinear model of the PA of the wireless transmitter
无线信道为Rayleigh多径衰落信道,单位脉冲响应如表4所示。

表4 Rayleigh衰落信道的单位脉冲响应Tab.4 The impulse response of the Rayleigh fading channel
实验中,通信帧的先验训练序列随机产生,调制模式分别为BPSK、QPSK或16PSK,通信帧长分别为1 024、2 048与4 096。该部分实验采用过采样技术,采样率为符号率的8倍。两无线设备发射机的基带发送滤波器均为升余弦奈奎斯特滤波器。
4.3.1分离实验
当待分离参数的无线设备为Transmitter-1、无线信道为Channel-1时,通信帧训练序列的调制模式设为BPSK,每个通信帧含1 024个基带符号,基带符号星座随机产生,共产生100个随机通信帧样本。


图10 调制模式为BPSK、不同通信帧长的分离性能Fig.10 The separation performance of BPSK signal under different length of communication frames
当SNR为20 dB时,100个帧得到的分离参数如表5所示。

表5 100个帧得到的分离参数Tab.5 The separated parameters with 100 frames
把表5中分离的Transmitter-1与Channel-1参数与表3与表4中的相应设定值对比可知,当SNR为20 dB时,两参数得到了较好的分离。
4.3.2分类实验
在不同SNR、不同通信帧长与不同调制模式下进行了基于f1与f2的分类实验。其中,每次分类实现的的训练样本个数为10,测试样本个数为10;k分别取为1、2、3。
当调制模式为BPSK,通信帧长分别为512、1 024与2 048时,把f1与f2的实部与虚部分别作为特征矢量,基于k-NN分类器统计得到的Transmitter-1/Channel-1与Transmitter-2/Channel-2的错误分类率随SNR的变化规律分别如图11与图12所示。

图11 调制模式为BPSK、不同k与不同通信帧长时的错误分类率(实部)Fig.11 The misclassification rate with different length of frame and k under BPSK modulation (real part)

图12 调制模式为BPSK、不同k与不同通信帧长时的错误分类率(虚部)Fig.12 The misclassification rate with different length of frame and k under BPSK modulation (imaginary part)
由图11与12可知,Transmitter-1/Channel-1与Transmitter-2/Channel-2的正确分类率随SNR的增加而增加,随通信帧长的加长而更优。
5 结束语
本文提出了一种根据通信帧的先验前导信号,采用两次LS估计对无线发射机PA非线性的模型系数与无线信道单位脉冲响应进行联合估计的方法,分别对多载波OFDM/单载波通信、PA有/无记忆、直接加取平均/迭代积累、算法趋势及分离/分类性能进行了数值仿真实验,结果显示了所提方法的正确性与有效性。所提方法可应用于无线网络设备的物理层射频指纹认证,以及无线通信的非线性信道估计与均衡等。
然而,有记忆MP模型下的估计精度仍不能满足实用要求,这是正在进行的研究工作。
[1] 彭林宁,胡爱群,朱长明,等. 基于星座轨迹图的射频指纹提取方法[J]. 信息安全学报,2016,1(1):50-58.
PENG Linning,HU Aiqun,ZHU Changming,et al. Radio fingerprint extraction based on constellation trace figure[J]. Journal of Cyber Security,2016,1(1):50-58. (in Chinese)
[2] ZHANG J,WANG F,OCTAVA A D. Specific rmitter identification via Hilbert-Hung transform in single-hop and Relaying scenarios[J]. IEEE Transactions on information Forensics and Security,2016,11(6):1192-1105.
[3] 张国柱,夏鲁宁,贾世杰,等. “牵星法”:一种基于射频指纹的高频RFID克隆卡检测方法[J]. 信息安全学报,2017,2(2):33-47.
ZHANG Guozhu,XIA Luning,JIA Shijie,et al. “Star drawing operation”:a method to identify HF RFID cloning card based on RF fingerprinting [J]. Journal of Cyber Security,2016,1(1):50-58. (in Chinese)
[4] GUNGOR O,KOKSAL C E.On the basic limits of RF-fingerprint-based authentication[J]. IEEE Transactions on Information Theory,2016,62(8):4523-4543.
[5] 袁红林,胡爱群,陈开志. 射频指纹的唯一性研究[J]. 应用科学学报,2009,27(1):1-5.
YUAN Honglin,HU Aiqun,CHEN Kaizhi. Uniqueness of radio frequency fingerprint [J]. Journal of Applied Science,2009,27(1):1-5. (in Chinese)
[6] 校莉. 射频信道非线性失真对多载波数字通信的影响及常用线性化技术分析[J]. 电讯技术,2011,51(7):122-127.
XIAO Li.Impact of non-linear distortion of RF channel on multi-carrier communication systems and analysis of commonly-used linearization technology [J]. Telecommunication Engineering,2011,51(7):122-127. (in Chinese)
[7] 刘顺兰,蒋树南. 非线性信道的均衡算法研究[J]. 电子学报,2010,38(10):2219-2223.
LIU Shunlan,JIANG Shunan. Equalization algorithms based on nonlinear channel[J]. Acta Electronica Sinica,2010,38(10):2219-2223. (in Chinese)
[8] 宋玙薇,杨守义,齐林. 基于维纳模型的非线性信道接收端均衡方案[J]. 电视技术,2012,36(5):83-85.
SONG Yuwei,YANG Shouyi,QI Lin. Receiving-end equalization scheme for nonlinear channel based on Wiener model[J]. Video Engineering,2012,36(5):83-85.(in Chinese)
[9] POLAK A C,DOLATSHAHI S,GOECKEL D L. Identifying wireless users via transmitter imperfections[J]. IEEE Journal on Selected Areas in Communications,2011,29(7):1469-1479.
[10] HUANG G,YUAN Y,WANG X,et al. Specific emitter identification based on nonlinear dynamical characteristics[J]. Canadian Journal of Electrical and Computer Engineering,2016. 39(1):34-41.
[11] 江立伟,袁红林,严燕,等.一种低信噪比下的高精度射频指纹变换方法[J]. 数据采集与处理, 2015, 30(5): 1036-1042.
JIANG Liwei, YUAN Honglin, YAN Yan, et al. High-accuracy radio frequency fignerprint transform method in low SNR environment[J]. Journal of Data Acquisition and Processing, 2015, 30(5): 1036-1042. (in Chinese)
[12] LIU M W,DOHERTY J F. Nonlinearity estimation for specific emitter identification in multipath channels[J]. IEEE Transactions on Information Forensics and Security,2011,6(3):1076-1085.
[13] LIU Y,CHEN H H,WANG L. Physical layer security for next generation wireless networks:theories,technologies,and challenges[J]. IEEE Communications Surveys & Tutorials,2017.19(1):347-376.
[14] TEHRANI A S,CAO H,AFSARDOOST S,et al. A comparative analysis of the complexity/accuracy tradeoff in power amplifier behavioral models[J]. IEEE Transactions on Microwave Theory and Techniques,2010,58(6):1510-1520.
[15] LIU M W,DOHERTY J F.Frequency-selective multiple-input multiple-output channel estimation with transmitter non-linearity[J]. IET Signal Processing,2009,3(6):467-475.
[16] IEEE.Wireless LAN medium access control (MAC) and physical layer (PHY) specifications:high-speed physical layer in the 5 GHz band:IEEE Std 802.11a-1999[S].[S.L.]:IEEE,2000:1-102.
[17] HEMESI H,ABDIPOUR A,MOHAMMADI A. Analytical modeling of MIMO-OFDM system in the presence of nonlinear power amplifier with memory[J]. IEEE Transactions on Communications,2013,61(1):155-163.
AKroneckerProductBasedParameterSeparationMethodforWirelessCommunicationSystems
YUAN Honglin,JIANG Liwei
(School of Electronics and Information,Nantong University,Nantong 226019,China)
For the problem of transmitter nonlinearity and wireless multi-path fading channel in wireless communication systems,a combined estimation of the nonlinearity of power amplifier (PA) and impulse response of wireless channel with the
signal is proposed. Firstly,a convolution matrix is constructed based on the training symbols and model structure of the nonlinearity,then once least squares (LS) is used to estimate the coefficients of the model of the PA and actual transmitted symbols through the PA. Secondly,the estimation of the impulse response of the wireless channel is obtained with another LS. And the integration of the two estimations can be iterative or with direct summation and mean. Theoretical derivation and experimental results demonstrate that the method can be used in single-carrier or multi-carrier communication with oversampling technology,and can separate the nonlinearity of PA and impulse response of wireless channel effectively. The novel method can be used for the physical-layer radio frequency(RF) fingerprint authentication and reliable signal transmission.
wireless channel;power amplifier nonlinearity;parameter separation;Kronecker product;radio frequency(RF) fingerprint identification;RF fingerprint authentication
10.3969/j.issn.1001-893x.2017.10.001
袁红林,江立伟.基于Kronecker积的无线通信系统参量分离方法[J].电讯技术,2017,57(10):1099-1106.[YUAN Honglin,JIANG Liwei.A Kronecker product based parameter separation method for wireless communication systems [J].Telecommunication Engineering,2017,57(10):1099-1106.]
2017-04-24;
2017-06-15 Received date:2017-04-24;Revised date:2017-06-15
国家自然科学基金资助项目(61371111);交通运输部应用基础研究项目(2012-319-813-270);江苏政府留学奖学金(University of Kent)项目
**通信作者:yuan.hl@ntu.edu.cn Corresponding author:yuan.hl@ntu.edu.cn
TN918.91
A
1001-893X(2017)10-1099-08

袁红林(1971—),男,江苏如皋人,博士,副教授,主要从事无线通信系统与信息处理的研究;
Email:yuan.hl@ntu.edu.cn
江立伟(1987—),男,江苏宿迁人,2015年于南通大学获硕士学位,现从事集成电路设计工作。
Email:jianglwxm@foxmail.com

