声波方程数值模拟矩形网格有限差分系数确定法

梁文全 王彦飞 杨长春

（①龙岩学院资源工程学院，福建龙岩364000；②中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室，北京100029）

声波方程数值模拟矩形网格有限差分系数确定法

梁文全①王彦飞*②杨长春②

（①龙岩学院资源工程学院，福建龙岩364000；②中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室，北京100029）

压制数值频散是有限差分方法的关键问题之一。目前压制数值频散的方法大多假设不同方向空间偏导数的空间步长相同，导致算法精度低，计算效率低。为此，提出使用线性方法压制声波方程矩形网格有限差分算子的数值频散，并进行了稳定性分析、频散分析和数值模拟。通过频散分析和数值模拟，验证了本文方法能够有效压制矩形网格有限差分数值频散，相较于泰勒展开方法和最小二乘方法，线性方法计算有限差分系数的效率更高，可以替代传统的正方形有限差分网格和相应的系数用于声波方程数值延拓。

声波模拟 时间—空间域 有限差分格式 矩形网格 数值频散

1 引言

地震波数值模拟延拓是地震学和勘探地震学的重要基础，在理论和应用中都发挥了重要的作用［1］。地震波数值模拟延拓的方法包括有限差分法、伪谱法、传统有限元法、谱元法、有限体积法、间断Galerkin法等［2，3］。有限差分方法因为计算效率高、所需内存小、实现简单而广泛应用于地震正演研究，同时是叠前逆时深度偏移成像、全波形反演、速度分析技术迅速发展的基础［4，5］。

数值频散是对波动方程的时间和空间偏导数的离散化造成的，使相速度变成了网格间距的函数，降低了模拟的精度。在地震波数值模拟中，一般使用正方形（正方体）差分网格进行数值模拟［6，7］。在实际地震资料处理中，需要使用矩形网格有限差分格式。Chen［8］基于平均导数法提出一种新的9点有限差分算子，可以解决频率—空间域数值模拟中不同方向空间采样间距不同的问题，并提高了频率域数值模拟的精度。Tang等［9］使用平均导数法优化了17点矩形网格有限差分格式在频率—空间域声波方程中的应用。Chu等［10］讨论了矩形网格（立方体）隐格式有限差分地震波数值模拟。但是鲜见对时间域矩形网格（立方体）有限差分算子系数如何确定的讨论，并且一般采用泰勒展开法确定有限差分系数［11］。为此本文使用效率较高的线性方法确定声波方程矩形网格的有限差分算子系数，以期提高地震波模拟的精度和效率。

通常在空间域确定波动方程空间偏导数的有限差分算子系数。但是，地震波在时间域和空间域同时传播，因此在时间—空间域确定空间偏导数的有限差分算子系数能同时抑制时间频散和空间频散。Liu等［12］通过平面波理论和泰勒展开方法在时间—空间域确定有限差分算子系数，在压制空间频散的同时压制了时间频散。Yang等［13］提出和改进了近似解析离散化方法以提高数值模拟的精度。Zhang等［14］提出使用模拟退火方法确定有限差分系数并指出选择合适的频散误差范围的重要性。Liu等［15］提出新的差分模板并用优化方法确定相应的系数，提高了数值模拟的精度。文中运用线性方法确定了声波方程矩形网格有限差分系数，并进行稳定性分析、频散分析和数值模拟，验证了本文方法的有效性。

2 有限差分算子确定方法

对于二维声波方程

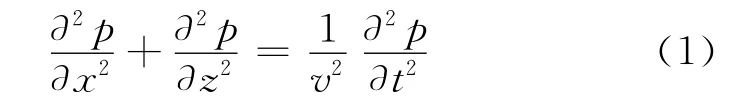
在（x，z）两个方向上的二阶空间偏导数，使用不同的空间步长计算，可以得到

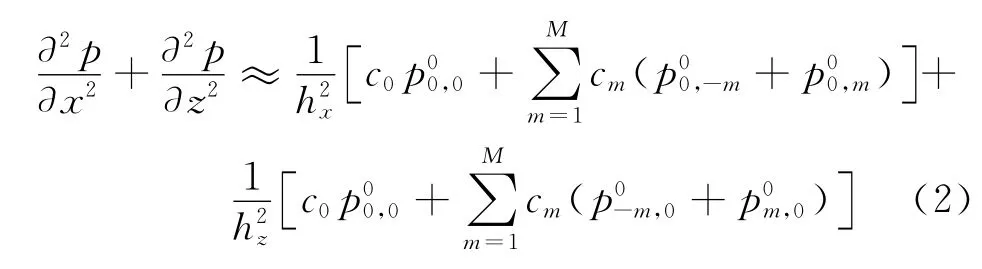
对于时间偏导数，采用二阶有限差分近似，得到

将式（2）和式（3）代入式（1），可得

对式（4）进行傅里叶变换，可得

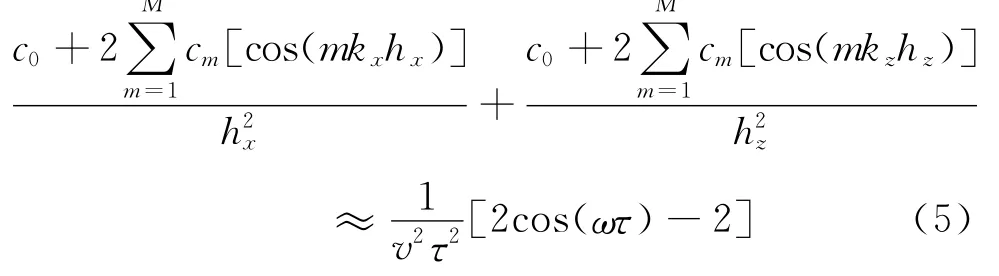
式中：k x=kcosθ，k z=ksinθ；k为波数；θ是平面波的传播角。

根据震源频率、波传播速度和网格间距确定需要满足频散关系的波数占总波数的比例［16］，即

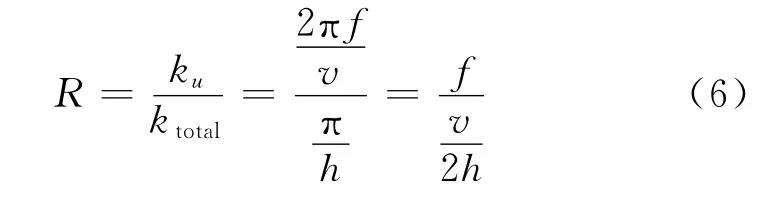
式中：f是震源最高频率；v表示地震波速度；h=max（h z，h x），假设h z＜h x；ku表示有限差分算子需要优化的波数；ktotal表示总的波数。

在式（6）确定的波数范围内，假设M+1个均匀分布的波数点满足式（5）所示的时间—空间域频散关系，则得到线性方程组

式中：ki，l（i=1，2，…，M+1；l=x，z）均匀分布于0和之间，而R通过式（6）确定；由式（7）可以确定声波方程矩形网格有限差分算子系数。

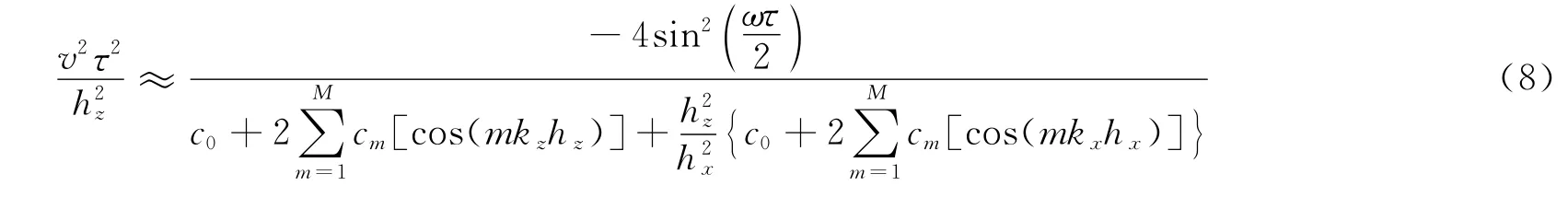
由式（5）可以得到一般来说，随着波数（频率）的增加，频散误差增大，令

将式（9）代入式（8），得到声波方程矩形网格有限差分算子的稳定性条件，即

图1是声波方程矩形网格有限差分算子的稳定性条件。从图1可以看出，在hz确定时，h x越大，稳定的时间范围越大。以Marmousi模型为例，其最高波速为4700m／s，假如hz=h x=4m，则其最大时间步长≤0.46ms；假如h z=4m，h x=12.5m，则其时间步长可以达到0.6ms。

3 频散分析

二维声波方程数值频散定义为［17］

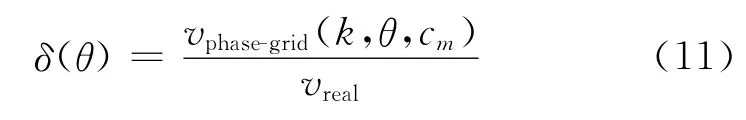
式中：vphase-grid表示离散相速度；vreal表示真实相速度；1-δ（θ）表示数值频散，1-δ（θ）的绝对值越小，数值频散越小。

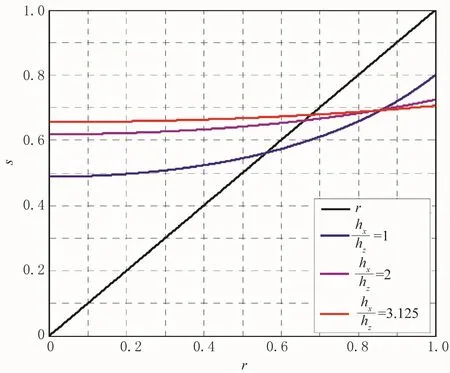
图1 矩形网格有限差分的稳定性条件

有限差分方法在一个空间网格上传播的时间误差为［17］

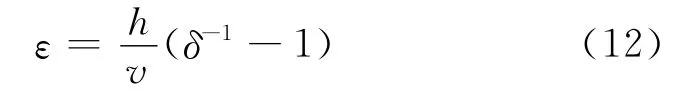
图2为泰勒展开方法和本文方法确定的矩形网格有限差分系数的数值频散，以M=30，τ=0.5ms泰勒展开方法作为近似解析解。由图2可以看出，在kh∈［0，2.5］范围内，本文方法的数值频散（图2b、图2e）要小于泰勒展开方法的数值频散（图1a、图1d），而接近于近似解析解数值频散（图1c、图1f）。

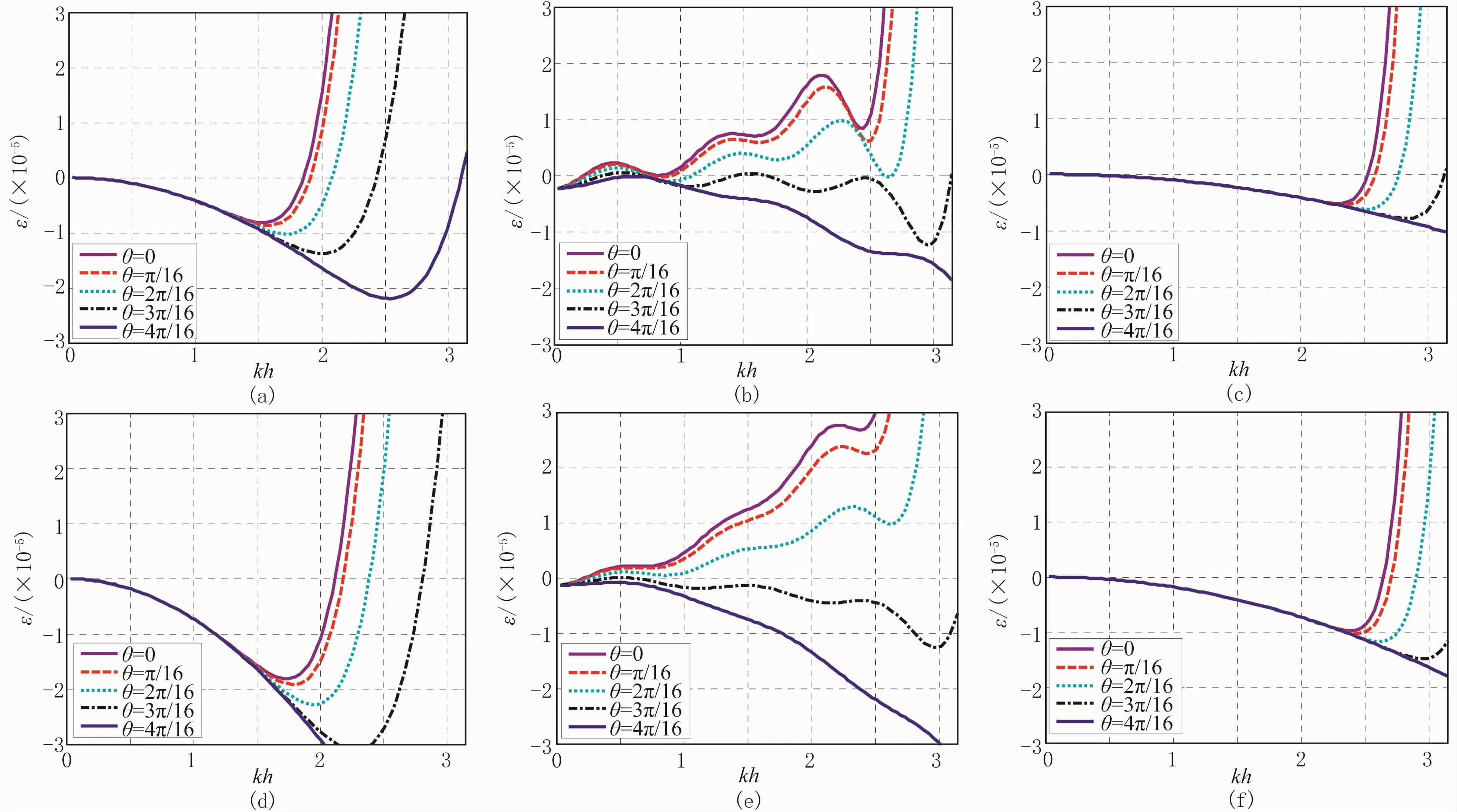
图2 不同方法矩形网格有限差分系数数值频散误差

4 数值模拟

4.1 均匀介质模型

首先考虑均匀介质模型，对于所有有限差分算子v=2000m／s，h z=10m，h x=20m，τ=1ms，M=7。模型网格数为350×700。震源在模型的中心位置，震源是高斯函数的二阶导数［18］，即

式中：f0=55Hz；是主频频率；c是常数。

图3为不同有限差分算法对应的1500ms时的波场快照及t=1500ms时的横向地震记录。使用τ=0.5ms，M=30的传统泰勒展开方法有限差分算子系数模拟结果作为近似解析解。由图可见，对于各种方法确定的有限差分算子系数，z方向的网格间距小，数值频散都不明显；x方向网格间距较大，数值频散明显（图3a、图3b）。由图3d、图3e以及泰勒方法和本文方法与近似解析解方法的残差（图3f）可见，较泰勒展开方法，本文方法压制了数值频散，更适用于确定矩形网格有限差分算子系数。对比图3d和图3f可知直达波的误差达到了10%左右，主要是由于本文方法时间步长较大引起的。如果将图3b和图3c的时间步长各缩小为原来时间步长的一半，则直达波的误差可以限制在2.5%以内。

图3 不同有限差分方法对应的1500ms处波场快照（上）及t=1500ms时的横向地震记录（下）

4.2 双层介质模型

不同的采样间隔比dx／dz显著提高了地震波数值模拟的效率，但是对地震记录的走时有较为显著的影响。例如一个双层介质模型，从0～1000m深度的波速是2000m／s，大于1000m深度的波速是2500m／s（图4a）。深度z方向分别采用5、10、20m的网格划分，其界面深度分别在1002.5m（200.5×5m），1005m（100.5×10m），1010m（50.5×20m图4b），因此造成了地震记录走时的不同。双层介质模型（图4a）得到的地震记录如图4c（震源在地表）所示。三种采样间隔比得到的单道地震记录如图4d（震源处接收）所示。由图4e和图4f可知，当深度z方向分别采用5、10、20m的网格划分时，其反射波第一个波峰时间分别是1076、1080、1086ms。dz=5m与dz=10m时网格划分走时相差4ms（理论上是2.5ms），dz=10m与dz=20m网格划分走时相差6ms（理论上是5ms）。因此网格间隔比的设计要根据实际情况综合考虑计算效率和精度。

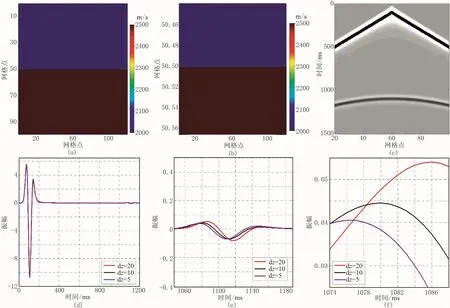
图4 双层介质模型地震波数值模拟结果

4.3 Marmousi模型

图5为Marmousi速度模型。震源函数采用式（13），其中震源频率f0=70Hz。对于所有的有限差分算子hx=12.5m，hz=4m。使用单程波和双程波混合边界条件压制边界反射［19］。图6为不同有限差分算子对应的地震记录及t=600ms时的横向地震记录。其中传统泰勒展开方法时间步长τ=0.6ms，M=7；本文方法时间步长τ=0.6ms，M=7；以τ=0.3ms，M=30的泰勒展开法数值模拟作为解析解。从图6a～图6c可以看出，本文方法较传统泰勒展开方法在相同算子长度和时间步长时有效压制了空间频散（图中框内），效果更接近于近似解析解。图6d～图6f比较了600ms时的横向地震记录（z=0），同样可以看出，本文方法有效地压制了数值频散。

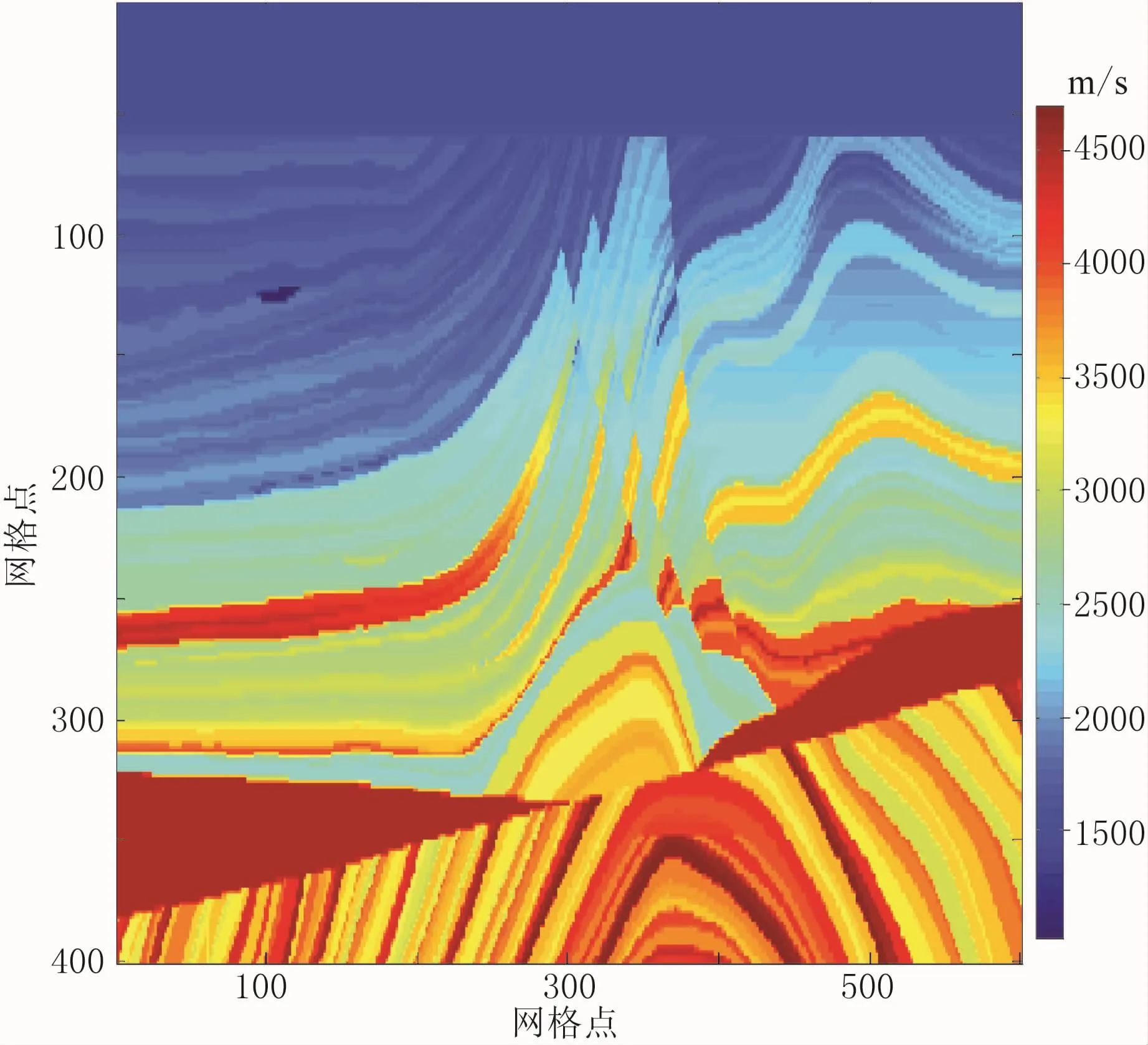
图5 Marmousi速度模型

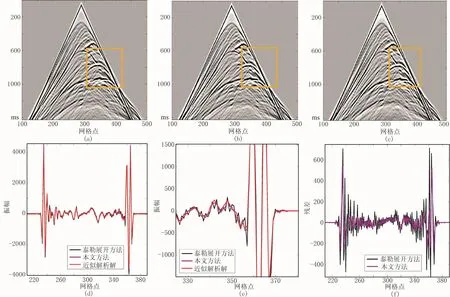
图6 不同有限差分方法对应的地震记录（上）及t=600ms时的横向地震记录（下）

5 结论

（1）在相同算子长度和时间步长时本文方法较传统泰勒展开方法有效地压制了空间频散，效果更接近于近似解析解。

（2）不同的网格间隔比dx／dz显著提高了地震波数值模拟的效率，但是对地震记录的走时有较显著的影响，因此网格间隔比的设计要根据实际情况综合考虑计算效率和精度。

（3）通过频散分析和数值模拟，验证了本文方法能够有效压制矩形网格有限差分数值频散，相较于泰勒展开方法和最小二乘方法，线性方法计算有限差分系数的效率更高。因此本文方法可以替代传统的正方形有限差分网格和相应的系数用于声波方程数值延拓。

［1］ Dablain M A.The application of high-order differencing to the scalar wave equation.Geophysics，1986，51（1）：54-66.

［2］ De Basabe J D and Sen M K.Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations.Geophysics，2007，72（6）：T81-T95.

［3］ De Basabe J D and Sen M K.A comparison of finitedifference and spectral-element methods for elastic wave propagation in media with a fluid-solid interface.Geophysical Journal International，2015，200（1）：278-298.

［4］ Liu H W，Li B，Liu H et al.The issues of prestack reverse time migration and solutions with graphic processing unit implementation.Geophysical Prospecting，2012，60（5）：906-918.

［5］ 刘洋.波动方程时空域有限差分数值解及吸收边界条件研究进展.石油地球物理勘探，2014，49（1）：35-46.Liu Yang.Research progress on time-space domain finite-difference numerical solution and absorption boundary conditions of wave equation.OGP，2014，49（1）：35-46.

［6］ 梁文全，杨长春，王彦飞等.用于声波方程数值模拟的时间—空间域有限差分系数确定新方法.地球物理学报，2013，56（10）：3497-3506.Liang Wenquan，Yang Changchun，Wang Yanfei et al.Acoustic wave equation modeling with new time-space domain finite difference operators.Chinese Journal of Geophysics，2013，56（10）：3497-3506.

［7］ 张志禹，谭显波，黄璐瑶等.抗频散有限差分波动方程数值模拟及逆时偏移.石油地球物理勘探，2014，49（6）：1115-1121.Zhang Zhiyu，Tan Xianbo，Huang Luyao et al.Antidispersion finite difference simulation and reversetime migration for wave equations.OGP，2014，49（6）：1115-1121.

［8］ Chen J B.An average-derivative optimal scheme for frequency-domain scalar wave equation.Geophysics，2012，77（6）：T201-T210.

［9］ Tang X，Liu H，Zhang H et al.An adaptable 17-point scheme for high-accuracy frequency-domain acoustic wave modeling in 2D constant density media.Geophysics，2015，80（6）：T211-T221.

［10］ Chu C and Stoffa P L.Implicit finite-difference simulations of seismic wave propagation.Geophysics，2012，77（2）：T57-T67.

［11］ Chen H，Zhou H and Li Y.Application of unsplit convolutional perfectly matched layer for scalar arbitrarily wide-angle wave equation.Geophysics，2014，79（6）：T313-T321.

［12］ Liu Y，Sen M K.Acoustic VTI modeling with a timespace domain dispersion-relation-based finite-difference scheme.Geophysics，2010，75（3）：A11-A17.

［13］ Yang D，Lu M，Wu R et al.An optimal nearly analytic discrete method for 2D acoustic and elastic wave equations.Bulletin of the Seismological Society of A-merica，2004，94（5）：1982-1992.

［14］ Zhang J H，Yao Z X.Optimized finite-difference operator for broadband seismic wave modeling.Geophysics，2012，78（1）：A13-A18.

［15］ Liu H F，Dai H X，Niu F L et al.An explicit time evolution method for acoustic wave propagation.Geophysics，2014，79（3）：T117-T124.

［16］ Wang Y F，Liang W Q，Nashed Z et al.Seismic modeling by optimizing regularized staggered-grid finitedifference operators using a time-space-domain dispersion-relationship-preserving method.Geophysics，2014，79（5）：T277-T285.

［17］ Liu Y，Sen M K.A new time-space domain high-order finite-difference method for the acoustic wave equation.Journal of Computational Physics，2009，228（23）：8779-8806.

［18］ 王彦飞，斯捷潘诺娃I E，提塔连科V N等.地球物理数值反演问题.北京：高等教育出版社，2011.

［19］ Liu Y，Sen M K.A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation.Geophysics，2010，75（2）：A1-A6.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.009

梁文全，王彦飞，杨长春.声波方程数值模拟矩形网格有限差分系数确定法.石油地球物理勘探，2017，52（1）：56-62.

1000-7210（2017）01-0056-07

*北京市朝阳区北士城西路19号，100029。Email：yfwang＠mail.iggcas.ac.cn

本文于2015年11月3日收到，最终修改稿于2016年11月1日收到。

本项研究受国家自然科学基金项目（41325016，91630202）及福建省自然科学基金（2016J05104）和龙岩学院博士科研启动基金（LB2014010）资助。

（本文编辑：金文昱）

梁文全 讲师，1983年生；2006年获南阳师范学院计算机系学士学位；2009年获得中国地质大学（北京）地理信息系统专业硕士学位；2012年获得中国科学院地质与地球物理研究所固体地球物理专业博士学位；目前在龙岩学院从事地震波数值模拟、偏移及反演研究及教学工作。