多信息融合的近地表速度建模技术及应用

赵玲芝 谷跃民 张建中

（①中国海洋大学海洋地球科学学院，山东青岛266100；②东方地球物理公司研究院，河北涿州072750）

多信息融合的近地表速度建模技术及应用

赵玲芝*①②谷跃民②张建中①

（①中国海洋大学海洋地球科学学院，山东青岛266100；②东方地球物理公司研究院，河北涿州072750）

为了提高复杂区近地表速度模型的构建精度，提出并实现了基于多信息融合的近地表速度模型构建技术。采用协同克里金的插值方法，根据初至反演的近地表速度与近地表调查速度的相关性及变化趋势，确定对应的变差函数和用于插值的权系数，对速度变量进行协方差的空间估计，使横向的速度变化趋势既与大炮初至层析反演的结果较吻合，数值上又与近地表调查的结果基本一致。该方法可以提高复杂近地表速度模型的精度。在中国西部复杂区地震资料的应用取得了较好的效果，进一步验证了该方法的有效性。

大炮初至 近地表调查 近地表模型 协同克里金插值

1 引言

近地表速度模型的精度直接影响静校正及叠前深度偏移成像的效果，如何得到高精度的近地表速度模型一直以来是陆上地震勘探的难题之一。

为了获得高精度的近地表速度模型，许多工区开展了微测井和小折射等近地表调查，大炮初至层析反演技术也得到了广泛的应用［1］。对复杂区近地表速度建模的结果研究表明：近地表调查的速度基本代表了该位置近地表的垂向速度，精度较高，但平面上呈散点分布，横向密度低，分布不均匀，不易刻画速度的空间变化［2］；而大炮初至层析反演技术所反演的速度不只受炮点位置速度的影响，还受炮检距大小、射线追踪的空间分布特征及速度的空间变化等影响，反演的速度模型可以作为真实模型的“等效模型”，能反映近地表速度的变化趋势，但数值上与微测井、小折射的速度存在一定的差异。因此，仅靠单一类型的资料无法满足复杂区地震资料近地表建模精度的需求［3-5］，尤其无法满足叠前深度偏移浅表层速度精度的需求。为此，人们开展了大量的研究，期望获得高精度的近地表速度模型和更高精度的静校正量。为了提高近地表速度模型的精度，为叠前深度偏移提供有效的近地表速度模型，提出了多信息融合的近地表速度建模技术，建立更加符合实际的近地表模型。

2 方法原理

由于近地表调查速度约束初至层析速度模型会在约束点（近地表调查点：一般速度较低，走时长）周围出现显著异常（速度突高），导致反演的速度模型不能真实地反映近地表的变化（图1）。为此，基于多信息融合的近地表速度建模技术，利用离散的近地表调查速度和大炮初至层析反演速度的变化趋势，通过协同克里金插值技术将两者的有效信息进行融合，估算近地表任意一点的速度，建立较精确的近地表速度模型。该方法的应用前提是这两种速度数据是相关的。

协同克里金的插值公式为

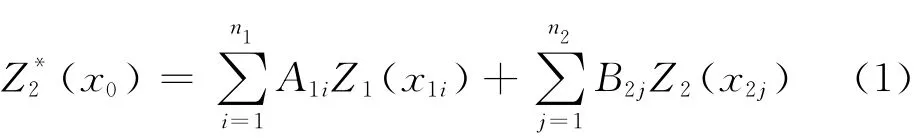
式中：Z1（x1i）为x1i处初至层析反演的速度（协变量，又称次变量）；Z2（x2j）为x2j处近地表调查的速度（主变量）；A1i和B2j分别为次变量、主变量的加权系数；是利用Z1、Z2两个变量的观测值加权平均预测的x0处的近地表速度值；n1、n2为Z1、Z2的个数，一般n1＞n2。

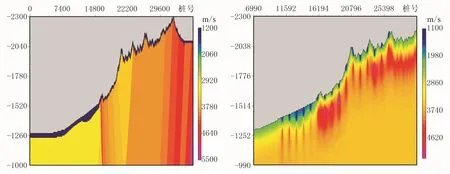
图1 理论速度模型（左）与点约束后的初至层析速度模型（右）

协同克里金估计方程组通过引入两个拉格朗日乘数u1和u2，利用克里金估计方法的无偏性和最小二乘法表示为

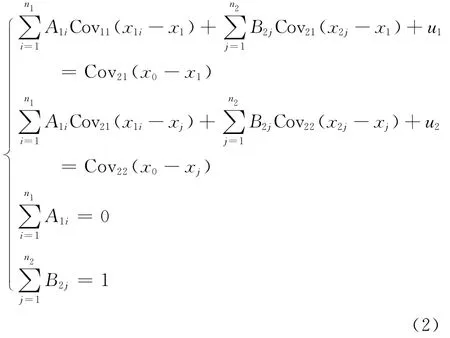
式中：Cov11和Cov22分别是Z1和Z2的协方差函数；Cov21为二者之间的协方差函数，其中Cov21=Cov12。由式（2）可知，只有求出准确的协方差函数，才能获得式（1）的权系数A1i和B2j以及两个拉格朗日乘数，然后通过克里金插值得到研究区域内任意点的插值估计。因此，协方差函数的估计是协同克里金插值的关键。

数学上协方差函数与变差函数是可以转换的，其关系为

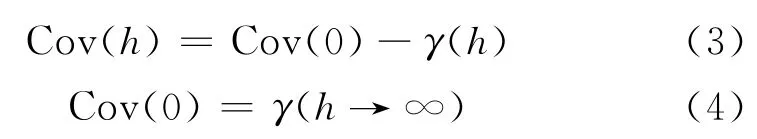
式中：γ为变差函数；h为两点的矢量距；Cov为协方差。由此可知：协方差与变差函数的关系是负相关，即随着变差函数的增加，其对应的协方差减小。因此，在进行协克里金插值之前，必须求取变差函数。

变差函数的主要含义为：当试验数据满足平稳性假设时，区域变量Z（x）在i方向上在x i和x i+h处的差的方差的其中，h为两点的距离。因此，变差函数与距离有关，它表示变量在空间的变异性（不相似性）［6-8］，即随着距离的变化，空间的变异程度也发生变化，距离越大，空间的变异程度越高，变量对插值的贡献就越小。

根据主、次变量的特点，变差函数可分为自变差函数和互变差函数（又称交叉变差函数），即

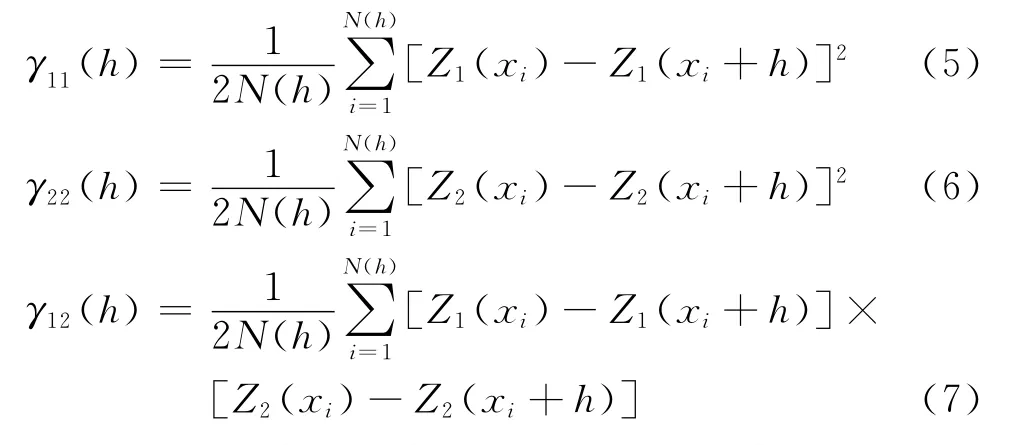
式中：γ22、γ11分别为主变量、次变量的自变差函数；γ12为二者的交叉变差函数，且γ12=γ21；N（h）是分割距离为h时的样本对数。

变差函数需要根据原始数据的特点选择相应的变差函数模型，不同的变差函数模型对插值的结果影响也不同。一个符合资料特点的变差函数模型可以较好地拟合样本的变异性，减少插值的误差，提高插值的精度，因此，变差函数模型的选取十分重要。常规三维资料通常选用球形模型，主要原因是球形模型具有灵活性大、适应性强的特点，适合各种复杂形状的变差函数［6-8］。

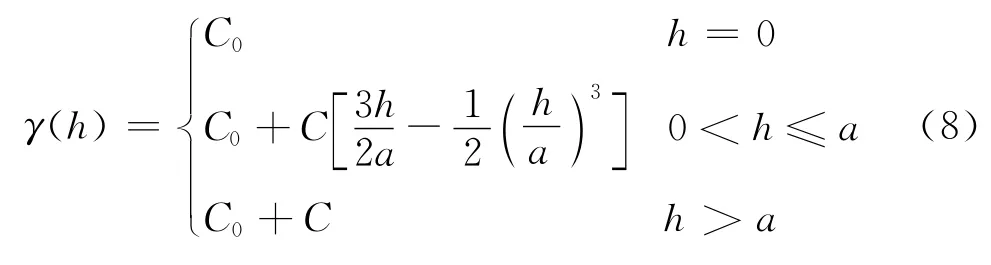
球形模型的变差函数为对应的变差函数曲线如图2所示。

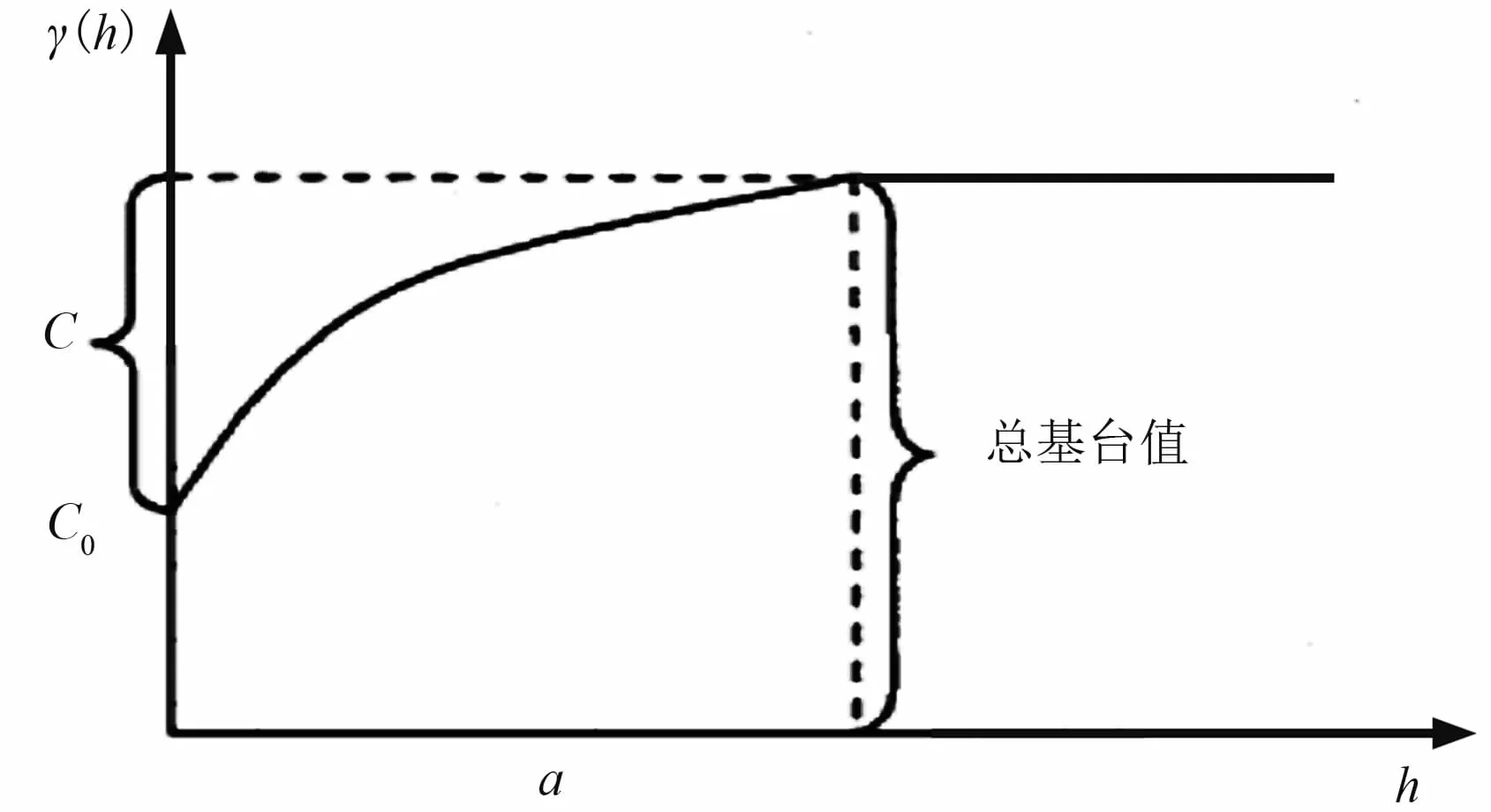
图2 球形模型的变差函数曲线

图2中a为变程，反映变量在空间上具有相似（关）性的最大距离。在变程范围内（当0＜h≤a时）数据是相关的，相关性随h的增大而逐渐减弱，用于插值的权重也随之降低，反之亦然；在变程范围外（当h＞a时）数据就失去了相关性，此时的变差函数一般等于协方差Cov（0）。由此可知，在进行多信息融合近地表速度建模时，如果观测点间距离大于这个范围，则此时数据的关系就表现为不相关，就不能用来求解。因此，本方法要求近地表调查点的分布不能太稀疏，且该范围内近地表调查与初至层析的速度具有相关性。

C0为块金值，是变程为零时的变差函数，相当于变量中的随机部分，表现为变量的不确定性。在应用过程中通常定义为0，也就是说变差函数在变程为零时与观测点的值保持一致。C为拱高，表示在变程范围内有效数据的变异性；C0+C为总基台值，反映变量在空间上（变程范围内）的总变异性大小，总基台值越大说明数据的波动程度越大，参数变化的幅度也越高。由此可知，原始变量的分布及变差函数的参数试验和确定是建立球形模型变差函数的关键，也是影响插值精度和效果的重要因素［12-15］。

应用球形模型对变量进行空间估计时，需要获取估计点周围的数据，其搜索数据的范围是一个球体的空间。因此，在球形模型中还需要定义球体的长轴、短轴和中长轴变差函数的变程（分别对应于主变程、垂直变程和次变程）及相应的变差函数参数（块金、拱高、基台），同时，还需要定义球体的空间走向，这就是变差函数的方位参数。也就是说求解球形模型的变差函数时需要确定三个轴方向的变程、块金、拱高、基台和方位等参数。

确定变差函数之后，可根据式（3）计算出对应的协方差，代入式（2）即可求出式（1）中的次变量、主变量的加权系数，进而得到空间区域内经过协同克里金插值的速度，这就是将近地表调查和初至层析的速度进行融合的高精度近地表速度。

通过以上分析可知，基于多信息融合的协同克里金近地表速度建模技术是利用近地表调查速度与初至层析反演速度的相关性，考虑到插值点与主、次变量的距离，对这两个变量进行加权平均，使得插值的结果既忠实于近地表调查的速度精度，又忠实于初至层析反演的近地表速度模型的空间关系，达到提高近地表不同位置速度精度的目的。

3 实现步骤

（1）对数据进行分析，确定二者的相关性。协克里金插值要求主、协变量数据间在变程范围内具有相关性。因此，在插值之前需要对近地表调查点与初至层析反演的相同位置的速度进行相关性分析，确保二者具有相关性，对不具有相关性的数据进行分析和删除，确保数据的合理性和有效性。

（2）对数据进行整理和采样。由于近地表调查的速度（如小折射、微测井等）垂向采样较为稀疏，且每个数据的垂向采样不规则，而初至层析的近地表速度模型垂向采样为等间隔的规则采样，为此需要对近地表调查的数据重采样，使近地表调查速度的采样与初至层析反演的速度垂向采样一致，便于后期的速度插值和建模。

（3）求变差函数，建立近地表深度速度模型。根据数据的特点，依据已有的数据类型、精细程度以及地表的复杂性等，选择并确定球形模型的相关参数并进行协同建模。试验确定球形模型三个轴方向的三个变差函数（近地表调查速度的变差函数、初至层析反演速度的变差函数及二者的交互变差函数）及其对应的参数（块金值、拱高、基台、变程等），然后根据变差函数确定协克里金插值的权系数，进行插值并平滑插值结果，形成最终融合的近地表速度模型。

4 应用实例

在以上分析研究的基础上，选择一个典型的具有复杂近地表的山地三维地震工区，开展相关的应用研究。

由于该区近地表复杂，近地表速度模型的合理构建及静校正量的计算一直是影响该区地震资料后续处理的关键因素。因此，在野外开展了近地表调查，调查点较多且呈散点分布（图3的离散点）。为了能够精细描述近地表速度的变化特征，近地表调查点的布设相对比较均匀。尽管如此，仍不能满足近地表速度建模的需求；利用初至层析技术反演的结果也不理想。因此，考虑采用多信息融合的近地表速度建模技术，充分利用二者的优点，提高近地表速度建模的精度。

在融合速度建模之前，首先分析近地表调查与初至层析反演的速度的相关性。图3是该区近地表调查的速度（离散的点）与初至层析反演的近地表速度（连续的面）叠合图。由图可见，二者所反映的速度趋势基本一致。沿图中黑线拉出一条初至层析速度剖面（图4a），量化分析过剖面某一位置（图4a中黑线）的微测井速度与初至层析反演速度的时深关系曲线（图4b）。从图4b的量化分析图中可以看出，初至层析反演的速度与微测井计算的速度变化趋势基本一致，说明二者是正相关，但在数值上存在差异，初至层析的速度一般要高于微测井的速度。因此，需要利用近地表调查速度模型的可靠性与初至反演速度模型的规律性及二者的相关性，通过多信息融合的协同克里金插值建模方法构建近地表速度模型，以提高近地表速度模型的精度。

图3 近地表调查与初至层析反演的近地表速度叠合图

其次，对近地表调查点的速度进行垂向采样。在对近地表调查点的速度进行垂向采样时，为了提高采样的合理性，通过研究和试验，提出并实现了慢度域平滑采样技术（即对每点的速度倒数进行平滑），然后再做重采样。

最后，求取变差函数，进行多信息融合速度建模。如前所述，在进行多信息融合的速度建模过程中，所应用的变差函数模型是球形模型。为了构建该模型，需要试验和求取一些基本参数，比如：球体空间展布方位及主变量、次变量、主次变量交叉的变差函数在球体三轴方向的相关参数。

根据工区不同位置的速度变化趋势确定球体的主轴方位分别是68°、55°、115°、145°。68°方位描述的是浅表层速度的变化趋势，55°是由物源方向决定的速度趋势，115°和145°分别描述的是高速层速度的变化规律，由本区的构造长轴和剥蚀背景决定。

根据以上方向分别计算相应的主变量、次变量及主次变量交叉的变差函数，同时拟合出不同球体所对应的长轴、短轴和中长轴的变程以及其他相关参数。不同方位的三维球形变差函数模型参数详见表1～表3。表1是主变量（近地表调查速度）不同方位的变差函数参数；表2是次变量（初至层析反演速度）不同方位的变差函数参数；表3是主次变量（近地表调查速度与初至层析速度）不同方位的交叉变差函数参数。图5是55°方位球形模型对应的三个变差函数。通过对比可以看出，对于待插值的目标区，在不同的位置及不同的方位，需要描述的变量特性是不同的，其对应的变差函数也不同，对插值的贡献也随之变化。

图4 近地表微测井与初至层析近地表模型的量化关系

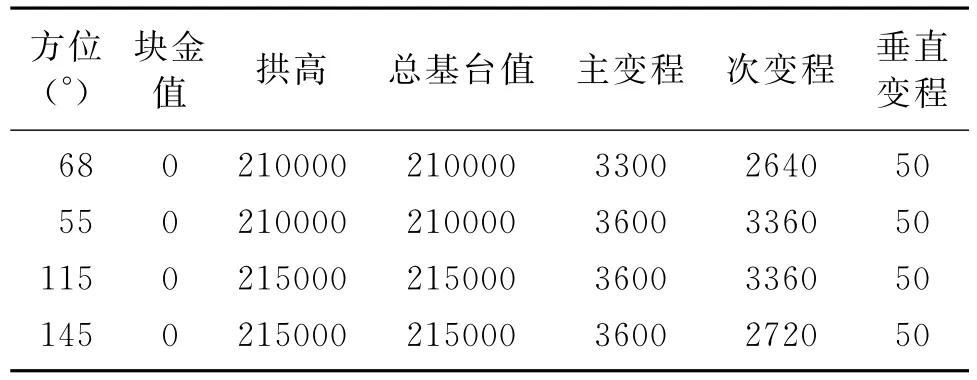
表1 主变量（近地表调查速度）不同方位的变差函数

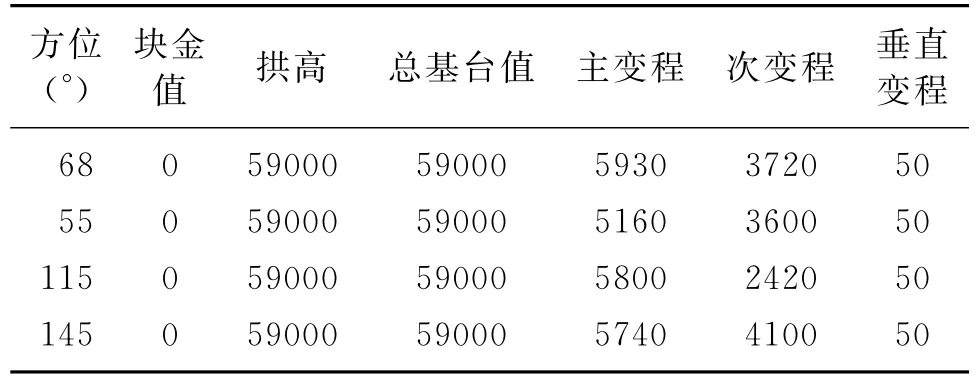
表2 次变量（初至层析反演速度）不同方位的变差函数

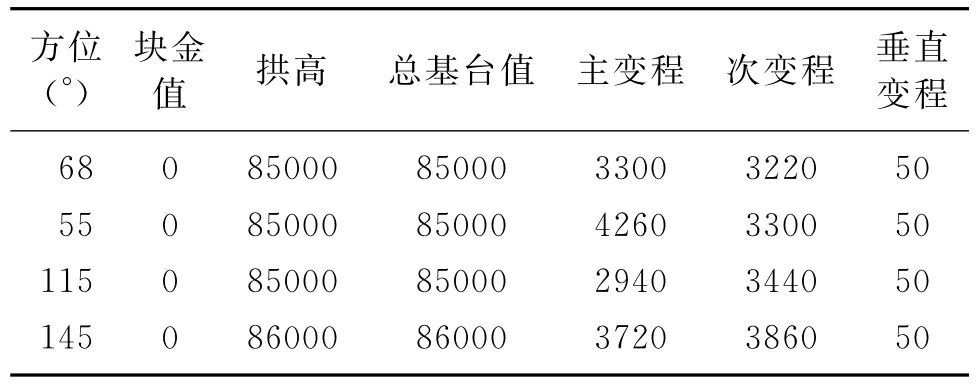
表3 主次变量（近地表调查速度与初至层析速度）不同方位的变差函数

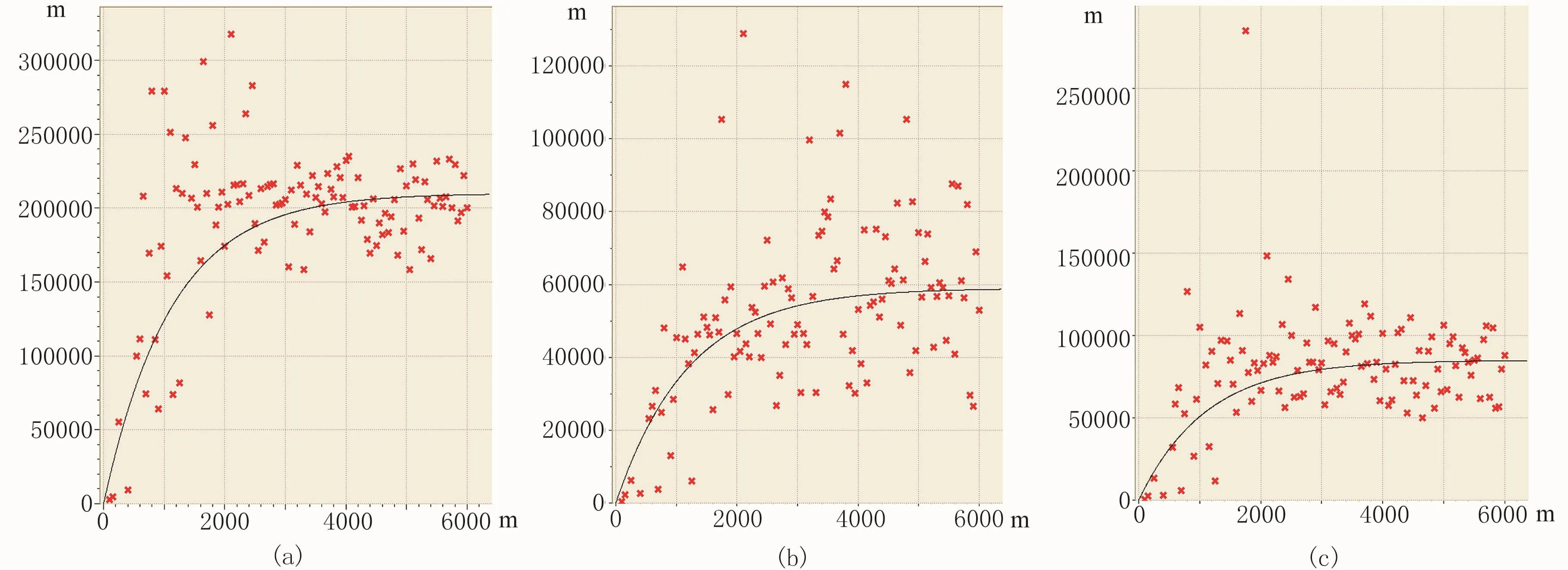
图5 55°方位球形模型对应的三个变差函数

根据以上变差函数，求取主、次变量的权系数，然后通过协同克里金插值形成相对精确的近地表速度模型。

图6为大炮初至层析与多信息融合协克里金插值的速度模型对比。可以看出，多信息融合近地表速度模型（图6右）与大炮初至层析反演速度模型（图6左）的速度趋势基本一致，速度值等同于近地表调查的速度。图7为近地表调查控制点处多信息融合的速度与原始近地表调查速度在地表下50m处的深度切片的速度交会图。可以看出，经过多信息融合的速度与近地表调查的速度值比较接近。图8是该区一个近地表调查点处的微测井速度、初至层析速度及多信息融合速度的垂向对比。可以看出，初至层析浅表层的速度由于缺乏小炮检距的信息及射线追踪方向主要沿地表，因此浅表层的速度偏高，深层速度由于受旅行时一致性的影响而偏低，经过多信息融合后，速度向近地表调查的速度靠近，速度趋势保留了初至层析速度模型的特点。

通过以上应用及分析不难看出，基于多信息融合的近地表速度模型构建技术利用了近地表初至层析速度的合理趋势，解决了稀疏近地表调查信息所引起的速度横向插值精度低的问题，充分利用了两者的优势，提高了近地表速度模型的精度。

为了进一步检验本文方法在实际资料中的适用性，用多信息融合的近地表速度模型与初至层析反演的速度模型分别计算静校正量，并应用于地震数据处理中，通过叠加剖面检查该方法所建立模型的精度。图9左是应用初至层析反演的近地表速度模型计算的静校正量的叠加剖面，图9右是应用多信息融合近地表速度模型计算的静校正量的叠加剖面。通过对比可以看出，初至层析近地表叠加剖面浅、中、深层的同相轴连续性较差，串相位问题突出，信噪比低（图9左）；多信息融合近地表叠加剖面的浅、中、深层信噪比和连续性都得到了较大提高（图9右）。说明多信息融合近地表速度模型是合理和准确的，较初至层析的速度模型精度高。图10是应用初至层析的近地表速度模型与多信息融合的近地表速度模型的叠前深度偏移剖面对比。可以看出，多信息融合近地表叠前深度偏移剖面浅、中、深层构造偏移归位精度明显高于初至层析近地表偏移。

图6 大炮初至（左）与多信息融合协克里金插值（右）速度模型对比

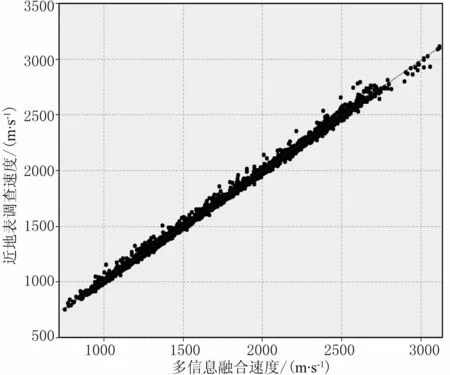
图7 近地表调查控制点处多信息融合的速度与原始近地表调查速度交会图

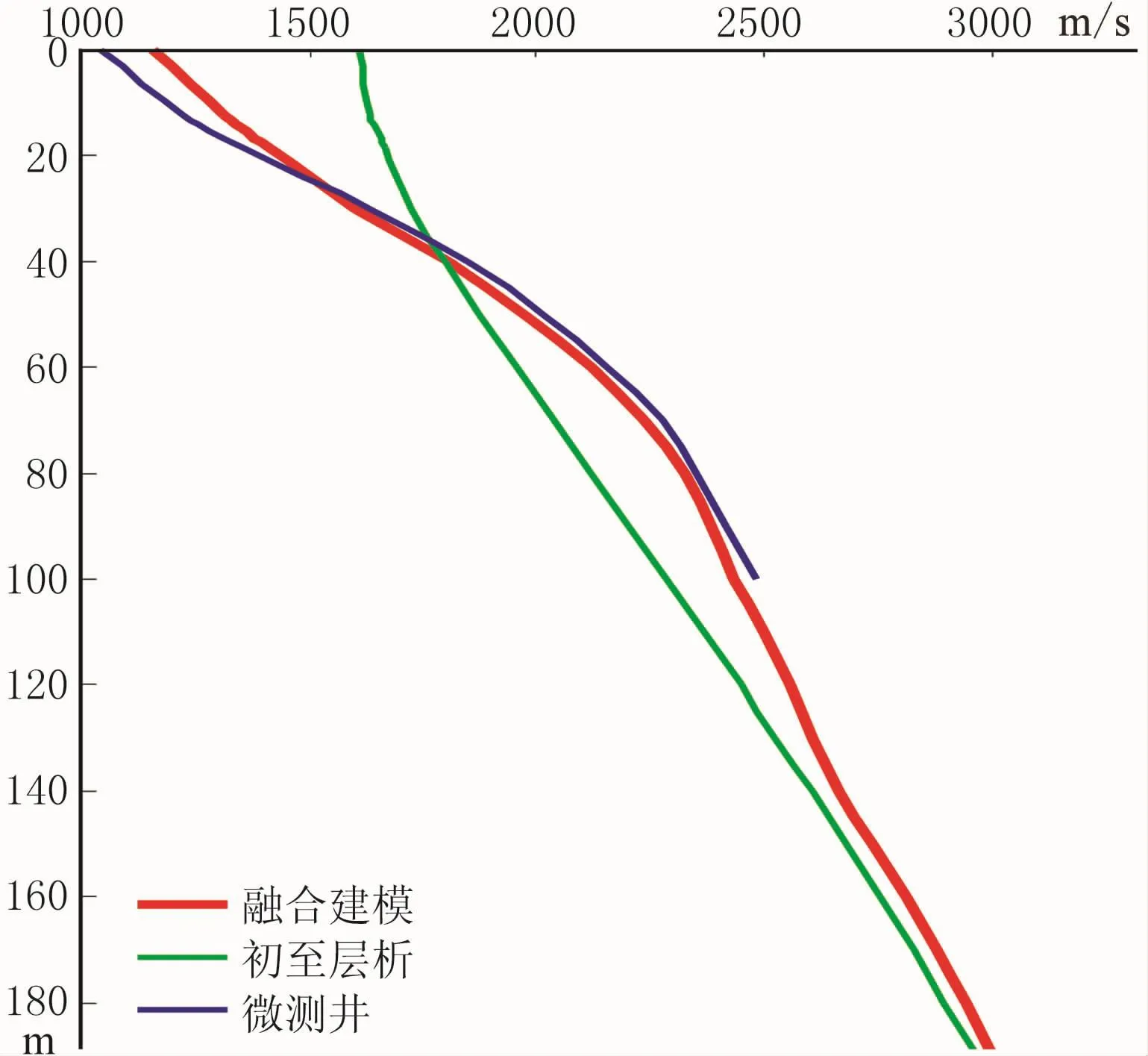
图8 近地表调查速度、初至层析速度与多信息融合的垂向速度对比

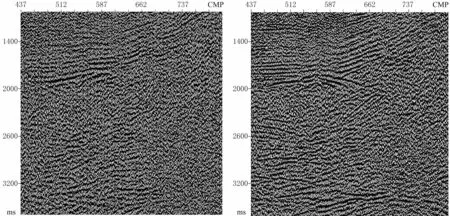
图9 应用初至层析近地表速度模型（左）与多信息融合近地表速度模型（右）计算的静校正量的叠加剖面对比

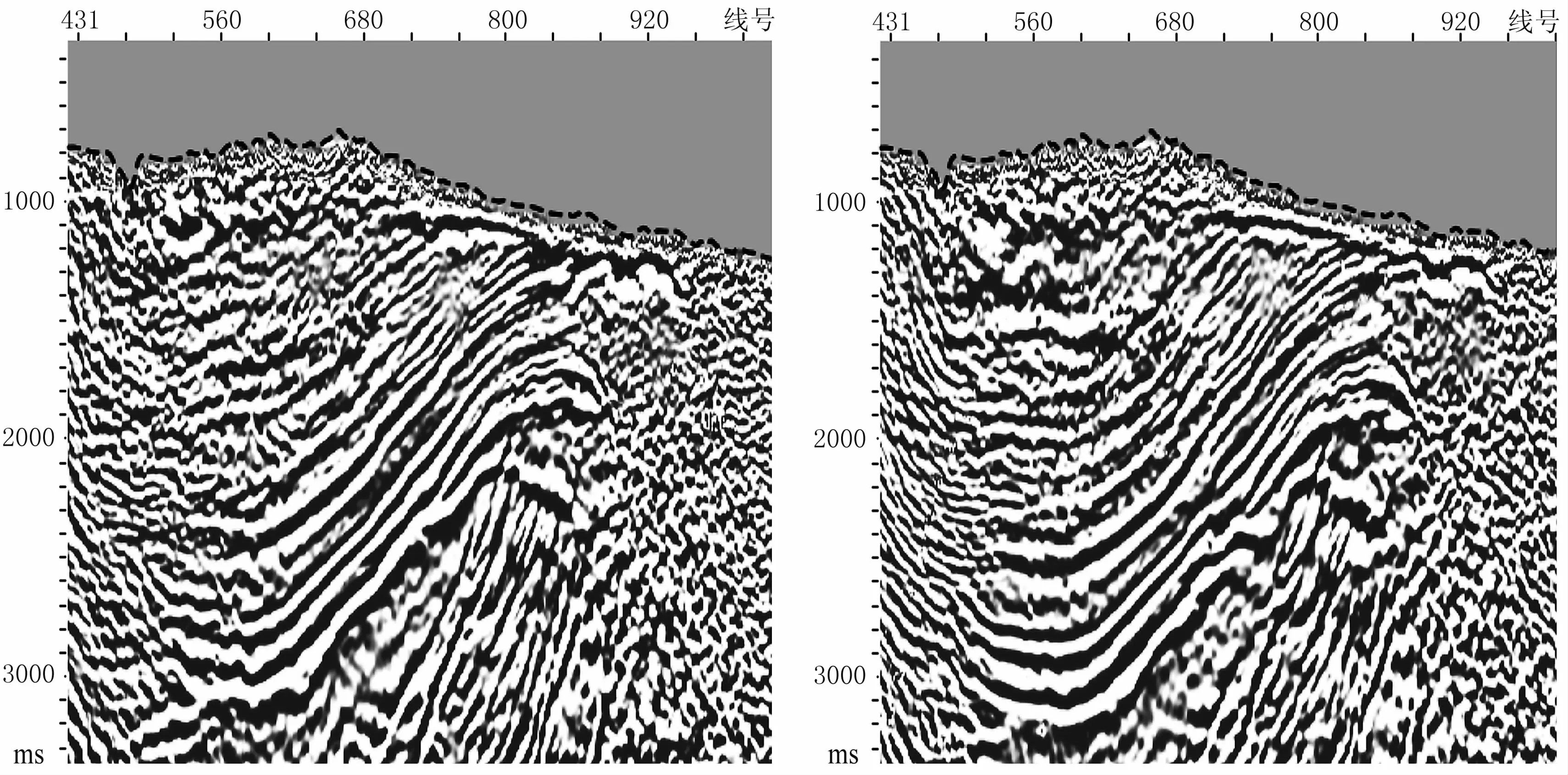
图10 应用初至层析近地表速度模型（左）与多信息融合近地表速度模型（右）的深度偏移剖面对比

5 结论

（1）近地表速度模型是影响复杂地表区静校正计算精度及叠前深度偏移速度建模的关键因素，近地表速度模型的精度直接影响对地下介质的客观认识。因此，在复杂区有必要运用近地表速度模型的精细构建技术建立精确的近地表速度模型。

（2）实际地震资料处理结果表明，多信息融合近地表速度建模技术可充分利用近地表调查速度模型与初至层析速度模型的优势，弥补其缺陷，达到提高近地表速度模型精度的目的。

（3）需要指出的是，根据工区近地表速度的分布特点合理选取变差函数模型及参数是确保速度模型构建精度的关键环节；如果参数选取不当、模型与实际速度的分布特点不吻合会影响该方法的效果。同时，要求近地表调查点的空间分布不能太稀疏，在变程范围内具有相关性，对不具有相关性的点要进行分析和删除。因此，具有有效空间约束的近地表调查点的空间分布是该技术应用的前提。

致谢在研究过程中得到了东方地球物理公司采集技术支持部祖云飞、马清坡两位专家的支持和帮助，在此深表感谢！

［1］ 李录明，罗省贤.复杂三维表层模型层析反演和静校正.石油地球物理勘探，2003，38（6）：636-642.Li Luming and Luo Xingxian.Tomographic inversion for 3-D complex near-surface model and static correction.OGP，2003，38（6）：636-642.

［2］ 王彦春，余钦范，李峰等.交互迭代静校正方法.石油物探，1998，37（2）：63-70.Wang Yanchun，Yu Qinfan，Li Feng et al.The method of static correction by interactive iteration.GPP，1998，37（2）：63-70.

［3］ 王振宇，杨勤勇，李振春等.近地表速度建模研究现状及发展趋势.地球科学进展，2014，29（10）：1138-1148.Wang Zhenyu，Yang Qinyong，Li Zhenchun et al.Research status and development trend of near-surface velocity modeling.Advances in Earth Science，2014，29（10）：1138-1148.

［4］ Berryhill J R.Wave equation datuming before stack.Geophysics，1984，49（11）：2064-2067.

［5］ Zhou Zhengzheng.Velocity Model in Depth Domain.2012 SEG Workshop，2012，Beijing.

［6］ 周游，程时清，张敏等.储层建模中变差函数参数设置.西安石油大学学报（自然科学版），2010，25（5）：25-27.Zhou You，Cheng Shiqing，Zhang Min et al.Setting of variogram parameters in reservoir modeling.Journal of Xi＇an Shiyou University（Natural Science Edition），2010，25（5）：25-27.

［7］ 汪彦龙，刘金华，张挺等.一种基于 Markov模型和COSGSIM的插值方法.计算机辅助设计与图形学学报，2010，22（10）：1715-1720.Wang Yanlong，Liu Jinhua，Zhang Ting et al.An interpolation method using the Markov model and COSGSIM.Journal of Computer-Aided Design＆Computer Graphics，2010，22（10）：1715-1720.

［8］ 胡丹桂，舒红.基于协同克里金空气湿度空间插值研究.湖北农业科学，2014，53（9）：2045-2049.Hu Dangui，Shu Hong.Air humidity based on co-Kriging interpolation.Hubei Agricultural Sciences，2014，53（9）：2045-2049.

［9］ Mesnard L D.Pollution models and inverse distance weighting：Some critical remarks.Computers＆ Geoscience，2013，52（1）：459-469.

［10］ Oliver M A，Webster R.Kriging：A method of interpolation for geographical information systems.International Journal of Geographical Information Systems，1990，4（3）：313-332.

［11］ 孟令顺，朱仁学，周云轩等.泛克里金法在大庆油田徐家围子西北地区密度建模上的应用.石油物探，2001，40（1）：88-96.Meng Lingshun，Zhu Renxue，Zhou Yunxuan et al.Application of universal Kriging to the density modeling in northwestern Xujiaweizi area of Daqing oil field.GPP，2001，40（1）：88-96.

［12］ Hass A G，Viallix J R.Kriging applied to geophysics：The answer to the problem of estimates and contouring.Geophysical Prospecting，1976，24（1）：49-69.

［13］ Olea R A.Optimal contour mapping using universal Kriging.Journal of Geophysical Research，1974，79（A2）：695-702.

［14］ 高美娟，朱庆忠，张淑华等.利用贝叶斯-克里金估计技术进行储层参数预测.石油地球物理勘探，1999，34（4）：390-397Gao Meijuan，Zhu Qingzhong，Zhang Shuhua et al.Reservoir parameter prediction using Bayes-Kriging estimation technique.OGP，1999，34（4）：390-397.

［15］ 年静波，汤磊，刘喜武等.地质统计分析在地震资料砂泥岩分布预测中的应用.石油物探，2004，43（3）：278-282.Nian Jingbo，Tang Lei，Liu Xiwu et al.Application of geostatistical analysis in prediction of sand／shale distribution from seismic data：a case study.GPP，2004，43（3）：278-282.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.006

赵玲芝，谷跃民，张建中.多信息融合的近地表速度建模技术及应用.石油地球物理勘探，2017，52（1）：34-41.

1000-7210（2017）01-0034-08

*河北省涿州市华阳东路东方地球物理公司科技园研究院处理中心，072750。Email：843422508＠qq.com

本文于2016年5月3日收到，最终修改稿于同年10月28日收到。

（本文编辑：金文昱）

赵玲芝 高级工程师，1970年生；1994年毕业于江汉石油学院物探专业，获学士学位；2008年毕业于中国石油大学（北京）地质工程专业，获硕士学位；现在中国海洋大学攻读海洋地球物理学博士学位；主要从事近地表建模及叠前成像技术方面的研究与应用工作，发表论文多篇。