多路段元胞自动机交通流模型∗
梁经韵 张莉莉 栾悉道 郭金林 老松杨 谢毓湘
1)(国防科学技术大学信息系统与管理学院,长沙 410072)
2)(长沙学院计算机工程与应用数学学院,长沙 410022)
多路段元胞自动机交通流模型∗
梁经韵1)张莉莉1)栾悉道2)†郭金林1)老松杨1)谢毓湘1)
1)(国防科学技术大学信息系统与管理学院,长沙 410072)
2)(长沙学院计算机工程与应用数学学院,长沙 410022)
在经典单路段元胞自动机交通流模型的基础上,将多个路段视为一个道路系统,提出并研究了多路段条件下的交通流问题.针对多路段道路的特点,通过引入车辆流入规则、路口随机慢化规则和路口车辆流入规则,控制车辆从上一路段流入下一路段.首先提出了“汽车池”的概念,来控制每一路口车辆的流入;然后通过路口随机慢化,来模拟路口对交通的影响;最后,当车辆离开时,依直行率进入下一路段,实现车流的继续流动.同时,通过数值模拟,仿真了不同条件下的交通情况,对重要参数进行了研究.结果表明,出现了混合流这一新的现象,拥堵地段与非拥堵地段间存在明显的界限.拥堵往往最先从路口开始,然后蔓延到整个路段.多路段道路还存在临界突变的特性.随着车辆流入概率的增大,路口对平均速度和车流密度的影响愈加明显.当流入概率超过一定阈值时,车辆缓慢地增加也会引起整体道路通行能力的迅速下降.
多路段,交通流,元胞自动机,微观仿真
1 引 言
21世纪,机动车已成为主要的道路交通工具,交通问题也成为衡量城市发展的一个重要因素[1].交通流的非线性、复杂性和离散性使得物理学、数学等多学科的研究者投入交通流问题的研究[1−32].元胞自动机具有时间离散化、空间离散化、相互作用的局域化和动力学演化同步性等特点,与交通流问题的特性相符合,且规则简单、灵活可调、便于程序仿真,因此在交通流问题的研究中得到了广泛应用[7−32].
NaSch模型[13]是由Nagel和Schreckenberg在1992年最先提出的.模型制定了车辆的加速、减速、随机延迟和车辆位置更新等4条演化规则,为交通流问题的研究打下了基础.1996年,Fukui和Ishibashi[14]提出了FI模型,考虑了车辆的迅速加速,是交通流研究中的另一重要模型.基于NaSch模型,人们提出了许多改进模型[7−32],用于研究交通流的性质和解决不同条件下的交通流问题.2000年,王雷等[15]调整了后车的随机减速规则,提出了WWH模型.2003年,考虑到驾驶员的不确定性敏感预期行为,雷丽等[16]将随机延迟置于确定性减速之前,提出了敏感驾驶模型.彭莉娟和康瑞[17]融合了NaSch模型和FI模型,将驾驶员分为激进型、中立型和保守型三类,提出Driver-SDNaSch模型.2014年,张柠溪等[18]提出考虑动态车间距的车辆演化规则,改进了单车道的元胞自动机交通流模型,María等[19]提出了安全驾驶条件下的改进模型.2016年,Chen和Wang[20]考虑了非机动车辆对整体交通的影响,Zhao等[21]对行人横穿街道的影响进行了建模,邱小平等[22,23]考虑了车辆之间的安全距离,进一步发展了交通流模型.2017年,Bouadi等[24]对NaSch模型中的再进入现象进行了理论分析和解释.
当前的研究主要集中在单段的道路上.然而,在真实的交通中,情况却更加复杂.不同道路相互交错、相互影响,很难找到一条孤立的道路.在实际出行中,为了到达目的地,往往要经过多个路段.要提高整体的通行能力,对多路段的研究也迫在眉睫.多路段模型是指综合研究多个路段的交通流模型,且路段之间存在路口,不同路段可能有不同的路段长度、车道数、最高速度等有关参数.如图1所示,箭头代表车流方向,上一路段s的车辆可能会流入下一路段s+1,也有可能离开系统;下一路段的车辆包括上一路段流入的车辆和新进入的车辆.本文对单路段模型进行了调整和改进,首次提出并研究了多路段道路问题.
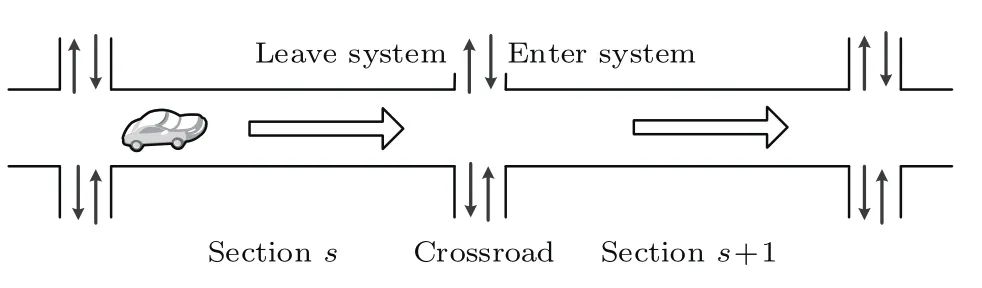
图1 多路段模型示意图Fig.1.Sketch of multi-section model.
多路段模型的难点在于处理不同路段车流之间的关系.在基于安全距离的交通流模型的基础上,本文引入了车辆流入规则、路口随机慢化规则和路口车辆流入规则,提出将不同路段串联起来,使上一路段的车辆能够“流入”下一路段,得到了多路段元胞自动机模型.同时,为了更好地了解多路段模型的性质,针对关键的参数如车流流入概率、路口最大速度和路口随机慢化概率等进行了相关实验,分析了时空图和车流密度等相关指标的变化规律.本文提出的多路段模型,可作为多路段道路建模的一个基本框架.通过该框架,可以将已有的单路段模型很好地迁移到多路段模型中来,从而更好地分析多路段条件下的交通变化规律.
2 多路段交通流模型
2.1 基本的单路段模型
单路段模型是指研究某一独立路段的交通流模型,在这一路段上,车道数、最高速度等有关参数视为相同.经典的单路段模型包括NaSch模型[13],FI模型[14],WWH模型等[15]. 本文的单路段模型主要基于NaSch模型,并考虑了Gipps安全距离[22,23−29].此外,针对多路段模型特点,引入了车辆流入规则.
NaSch模型是一个基于元胞自动机的单车道交通流模型,时间、空间和状态均离散.车道可以看做L个元胞组成的一维离散格点链,每一个格点在某一时刻最多被一辆车占据.第n辆车的状态由速度vn∈{0,1,···,vmax}和位置xn∈{1,2,···,L}表示,vmax代表允许的最高速度.所有的车辆按照定义的加速规则、减速规则、随机慢化规则和更新规则进行更新.考虑了Gipps安全距离和引入车辆流入规则后,具体演化规则如下.
1)计算安全距离[21,22]
为了保证行车安全,每一车辆必须与前一车辆保持适当的距离.过大的距离无法提高道路的整体交通流量,过小的距离则容易发生交通事故.Gipps安全距离是指当前一车辆紧急刹车时,车辆为了避免发生追尾而必须保持的一个安全距离.它可以综合考虑车辆的长度、加减速性能和司机的反应时间,动态地调整与前车所需保持的距离,进一步提高模型的精度.第n辆车与前方车辆的实际距离Gapn和Gipps安全距离Gapsafe,n的计算公式如下:

其中,xn(t)和xn+1(t)分别为t时刻第n辆车和其前方车辆所在位置,ln+1为前方车辆的长度,vn(t)和vn+1(t)分别为t时刻第n辆车和其前方车辆的速度,amax,n和amax,n+1分别为第n辆车和其前方车辆的最大减速度,τn为第n辆车驾驶员的反应时间.
2)加速规则
当第n辆车与前车的距离大于安全距离,即Gapn>Gapsafe,n时,为了更快地通行,车辆可以继续加速,加速度为aacc,n.在车辆行驶过程中,车辆速度应当保证不超过最大速度vmax和与前方车辆的距离Gapn.车辆按照如下规则加速:

3)随机慢化规则
为了更贴近实测数据,根据雷丽等[16]提出的敏感驾驶模型,优先考虑驾驶员的不确定性行为,将随机慢化规则放在减速规则之前.由于驾驶过程中的不确定性,引入随机慢化概率pbrake,以加速度adec,n进行随机减速.车辆按照如下规则进行随机慢化:

4)减速规则
当第n辆车与前车的距离小于安全距离,即Gapn<Gapsafe,n时,应当进行减速以确保安全.车辆按照如下规则进行减速:

5)位置更新规则
在速度更新之后,进行车辆位置的更新.当位置大于路段长度L时,视为车辆离开本路段,移除该车辆,路段总车辆数N减少.按照如下规则更新位置和移除车辆:

当xn(t+1)≤L时,N不变;当xn(t+1)>L时,有

6)车辆流入规则
考虑周期性封闭条件只适用于模拟环形公路或者一段高速公路的状态,没有新车辆的“流入”,本路段的车辆也无法“流入”下一路段,这并不合理.为了更准确地模拟和分析实际道路通行状况,采取开放式边界条件[30,31],增加了车流流入规则.可以依概率pin产生车辆,并根据当前道路状况决定是否进入道路,更符合真实场景,也便于管理部门调节交通.新的车辆进入或者上一路段的车辆流入下一路段时,需要长度为ln的空间.由于安全距离的限制,可能由于开始路段的车辆移动过慢而无法进入道路,导致道路流量降低.本文提出“汽车池”的概念来解决这个问题.每一次迭代,当p<pin时,新产生的车辆先进入汽车池中;若当前时刻道路上第一辆车的位置(以车头为准)大于其长度,即x1(t)>l1,新车辆从汽车池中进入车道,路段总车辆数增加.Ncarpool为汽车池中汽车的数量,N为路段总车辆数.按照如下规则更新汽车池和进入车辆:
当p≥pin时,Ncarpool不变;当p<pin时,有

当x1(t)≤l1时,Ncarpool和N不变;当x1(t)>l1时,有

2.2 多路段模型
在单路段模型的基础上,通过引入新的规则,将多个单路段模型串行连接,最终得到多路段模型.为了符合路口的特点和实现交通流在相邻路段之间的流动,增加了路口随机慢化规则和路口车辆流入规则.
7)路口随机慢化规则
与单路段模型不同,多路段模型某一路段的出口是有限制的.车辆临近路口时,由于交通信号灯处的等待或者其他车辆的转向等原因,速度会大大降低.参考经典NaSch模型中随机慢化的思想,引入整体的路口随机慢化概率pcross以简化问题,不具体分析交通信号灯等对车辆的影响.当车辆离路口的距离小于路口减速距离Gapcross,n且速度大于路口最大速度vcross时,以加速度across,n进行随机减速.车辆按照如下规则进行路口慢化减速:

8)路口车辆流入规则
当车辆从上一路段离开时,有直行和转弯两种可能.设车辆以直行率λ(λ∈[0,1])继续直行进入下一路段,且车辆的速度、驾驶员的反应时间等其他参数保持不变.设相邻的两个路段s和s+1的流量分别为Js和Js+1,λ0为最大直行率,Jnew为路段s+1新进入的车流量.当Js+1>λ0Js时,路段s+1的车辆由路段s直行的车辆和从路口新进入的车辆共同组成;当Js+1≤λ0Js时,可认为车辆大量离开本道路,新进入的车辆很少,路段s+1的车辆由路段s直行的车辆组成.相邻两个路段车流量关系满足下式:
当Js+1>λ0Js时,有

当Js+1≤λ0Js时,有

此外,考虑到转弯让直行的交通规则,直行车按照离开路段s的时间间隔依次进入路段s+1;新进入的车辆按照单路段中的车辆流入规则进入路段,当x1(t)>l1时先进入汽车池.
3 数值模拟与分析
3.1 仿真设置
数值模拟时,取两个路段s1和s2,长度L1=L2=3 km,每个道路元胞长为1 m,则每个路段被分为3000个格点.路段s1和s2新进入车辆的初始速度均为2—4 m/s,服从均匀分布.对于路段s1,上一路段到达本路段的车流量为零;对于路段s2,车流量包括来自路段s1的车流量和新流入的车流量,且来自路段s1的车辆的初始速度与离开路段s1时相同.经实验,路口减速距离Gapcross,n和直行率λ0的取值对交通流影响不大,实验中取Gapcross,n=200 m,λ0=0.9.模型规则中其他参数的取值如表1所列.使用加速规则和减速规则时,涉及Gipps安全距离的计算,对于计算得到的速度值,四舍五入取整.每一次模拟迭代2×104步,步长为0.5 s,统计时取后1×104步以消除暂态的影响.为了减少随机性的影响,每一组参数配置重复运行10次并取平均值.通过改变两个路段的车流流入概率pin,1和pin,2、路口最大速度vcross和路口随机慢化概率pcross模拟不同情况下的交通流状况.

表1 模型参数取值Table 1.Parameter value of model.
实验中用到的有关统计量的计算如下.记ρ为路段平均车流密度,v为路段平均速度,J为路段平均流量.由于边界条件是开放式的,每个时间步的车辆数不一定相同,各参数取每个时间步的平均值.

其中,T表示统计时所取的时间步数(从t0到T+t0−1),Nt表示t时刻的车辆总数,L为路段的长度,vn(t)表示第n辆车在t时刻的速度.计算整条道路的统计量时,则依据路段的长度取其加权平均值.
3.2 时空特征分析
图2为不同车流流入概率pin,1和pin,2下路段s1和s2的时空图,横轴方向为时间7500—7700 s,纵轴方向为位置0—3 km. 取路口最大速度vcross=6 m/s,路口随机慢化概率pcross=0.8.可以看出,随着pin,1和pin,2的增大,车流密度不断增大,道路拥堵程度也更加严重.
当pin,1和pin,2较小时,如图2(a1)和图2(a2),车流量相对较小,车流运行非常通畅,处于低密度的自由流状态[32],仅在靠近路口处偶尔有局部的拥堵情况,这与现实中车辆因为红灯等原因而在路口等待的情况是相符的.
当pin,1和pin,2增大时,如图2(b1)和图2(b2),车流整体运行平稳,路段上游车流密度加大,路口附近出现稳定的拥堵现象.此时,可以观察到一种新的混合流现象.不同于单路段模型,一个路段不再只处于自由流、同步流或者宽幅运动阻塞状态,而是可能为一种混合流的状态.路段上游处于自由流状态,路段下游处于同步流状态,两者之间有明确的分界线.图中的分界线可以视为路段开始拥堵的地点.由于到达车辆较多,而直行方向交通信号灯有时间限制,车辆在路口附近排队,往往需要等待一段时间才能通过路口,这与实际生活中路口的状况是相符的.且由于在路段s1末端车辆有减速和停滞,路口控制了车流的速度和流量,使得路段s2末端拥堵距离变短.这说明当车辆流入概率相同时,路段s1拥堵反而可能使得路段s2变得更顺畅.
当pin,1和pin,2继续增大时,如图2(c1)和图2(c2),车流密度较大,车辆通行不畅,整个路段出现拥堵,车辆速度时快时慢.当pin,1和pin,2极大时,如图2(d1)和图2(d2),整个路段出现严重拥堵,车流基本停滞,路段处于“堵死”状态.

图2 不同车辆流入概率下的时空图 (a)车辆流入概率pin,1=0.65,路段s2车辆流入概率pin,2=0.65;(b)pin,1=0.75,pin,2=0.75;(c)pin,1=0.85,pin,2=0.85;(d)pin,1=0.95,pin,2=0.95;(a1)—(d1)路段s1;(a2)—(d2)路段s2Fig.2.Space-time graph with di ff erent vehicle in flow probability:(a)Vehicle in flow probability pin,1=0.65 for section s1,vehicle in flow probability pin,2=0.65 for section s2;(b)pin,1=0.75,pin,2=0.75;(c)pin,1=0.85,pin,2=0.85;(d)pin,1=0.95,pin,2=0.95;(a1)–(d1)section s1;(a2)–(d2)section s2.
3.3 平均速度和平均车流密度
图3展现了不同车流流入概率pin,1和pin,2下整条道路的平均速度和平均车流密度的变化情况.实验中分别取车辆流入概率为0.1—1(间隔0.1)和0.82—0.9(间隔0.02),其他参数设置与图2相同.由图3可知,车辆流入概率对平均速度和平均车流密度有决定性的影响.当pin,1和pin,2在0.1—0.7之间时,如图3(a1)和图3(a2),平均速度保持在18.13 m/s附近几乎不变.此时,道路处于自由流状态,增加车辆的数量对平均速度影响很小,而平均车流密度处于缓慢增加状态.当pin,1和pin,2在0.7—0.8之间时,平均速度开始下降,说明车辆之间已经开始相互干扰.当pin,1和pin,2到达0.8后,平均速度急剧下降,并达到最小值7.35 m/s,平均车辆密度增加到0.1132 veh/m.当车辆继续增加时,由于安全距离的限制,车辆无法进入路段,达到最大车流量0.83 veh/s.由此可见,当车辆流入概率达到临界值后,继续增加车辆会极大地降低整体道路通行能力.进一步研究pin,1和pin,2在0.8—0.9之间的系统状态,如图3(b1)和图3(b2).可以发现,靠近临界值时,与pin,1相比,pin,2对平均速度的影响更大,改变pin,2的值,平均速度下降得更快.这说明,当车流量趋于饱和时,路段s2对于整个道路通行能力影响更大.

图3 (网刊彩色)不同车流流入概率下的速度与密度的变化 (a1)—(b1)速度;(a2)—(b2)密度;(a)pin,1=0.1,0.2,···,1,pin,2=0.1,0.2,···,1;(b)pin,1=0.81,0.82,···,0.9,pin,2=0.81,0.82,···,0.9Fig.3.(color online)Speed and density with di ff erent vehicle in flow probability:(a1)–(b1)speed;(a2)–(b2)density;(a)pin,1=0.1,0.2,···,1,pin,2=0.1,0.2,···,1;(b)pin,1=0.81,0.82,···,0.9,pin,2=0.81,0.82,···,0.9.
3.4 路口最大速度对交通流特性的影响
图4所示为路口最大速度vcross对整条道路交通流的影响.取路口随机慢化概率pcross=0.8.从图中可以看出,vcross取值对交通流的状态有较大的影响.当vcross较小时,大部分车辆到达路口前都经历了路口随机慢化的过程,速度很小.这导致道路平均速度v很小,路段s1和路段s2的流量J1和J2也很小,大量的车辆由于安全距离的限制无法进入路段,只能停留在汽车池中.当vcross增大时,v不断增大,同时,道路容量不断增大,使得J1和J2增大、Ncarpool减小.当vcross>10 m/s时,vcross对交通流的影响减小,系统各项指标趋于稳定.由图4(a)和4(b)可知,车流流入密度pin,1和pin,2较小时,对vcross的增长更为敏感,较小的vcross即可使v达到最大,使Ncarpool降为0,道路可以顺畅通行.由图4(c)和4(d)可知,当vcross较小时,pin,1和pin,2的取值对J1和J2的影响并不显著.当vcross较大时,pin,1和pin,2的取值影响增大.此时,通过改变pin,1和pin,2的值,可以很好地控制道路车流量.

图4 路口最大速度对道路交通流的影响 (a)速度;(b)汽车池车辆数目;(c)路段s1流量;(d)路段s2流量Fig.4.In fl uence of maximum crossroad speed on overall traffic:(a)Speed;(b)number of vehicles in car pool;(c)volume of section s1;(d)volume of section s2.
3.5 路口随机慢化概率对交通流特性的影响
图5展示了路口随机慢化概率pcross对整条道路交通流的影响.取路口最大速度vcross=6 m/s.当pin,1和pin,2取值较小时,pcross对道路交通流各项指标影响很小,平均速度v、汽车池大小Ncarpool、流量J1和J2都较为稳定.当pin,1和pin,2较大时,pcross对交通流影响较大.如图5(a),当pcross>0.4时,pin,1=0.85,pin,2=0.85和pin,1=0.95,pin,2=0.95对应的道路平均速度先后下降,最终稳定在6.8 m/s附近.而且,pin,1和pin,2取值越大,交通流对pcross的取值越敏感.如图5(b),当pcross>0.5和pcross>0.8时,pin,1=0.95,pin,2=0.95和pin,1=0.85,pin,2=0.85对应的道路容量分别接近阈值,车辆无法流入路段,Ncarpool不断增大.如图5(c)和5(d),流量J1和J2随pcross的增加逐渐下降.pin,1和pin,2越大,J1和J2下降得越快.且流量J2的下降幅度略大于流量J1,说明pcross对路段s2影响更大.
4 结 论
本文在单路段交通流模型的基础上,建立了多路段模型.核心思想是通过引入车辆流入规则、路口随机慢化规则和路口车辆流入规则,使得车辆能够从上一路段流入下一路段,实现对多个路段车辆的控制.同时,通过数值模拟,分析了不同车辆流入概率下多路段道路的基本时空图和速度与密度的变化情况,并探讨了路口最大速度和路口随机慢化概率等关键参数对多路段交通流的影响.
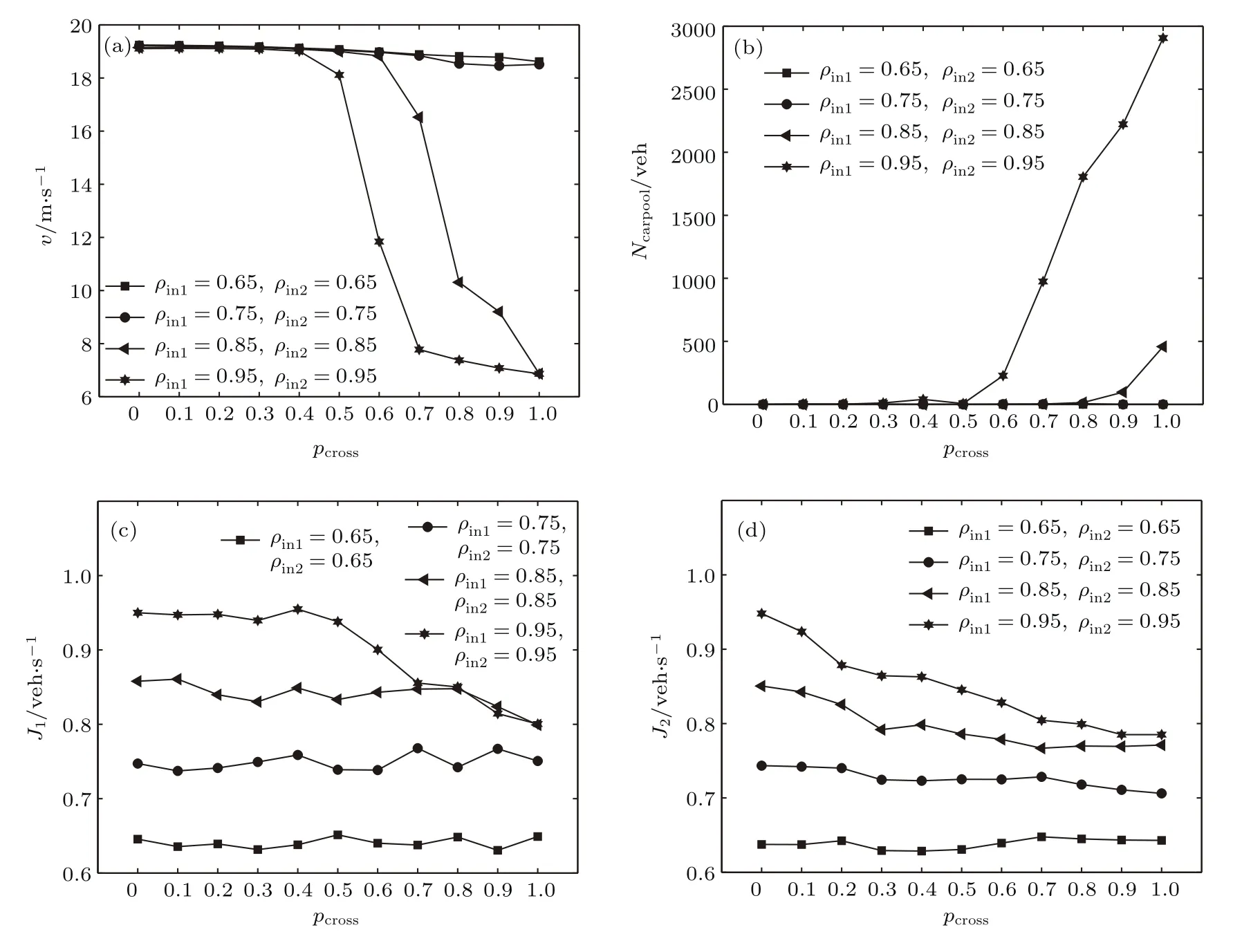
图5 路口随机慢化概率对道路交通流的影响 (a)速度;(b)汽车池车辆数目;(c)路段s1流量;(d)路段s2流量Fig.5.In fl uence of crossroad randomization brake probability on overall traffic:(a)Speed;(b)number of vehicles in car pool;(c)volume of section s1;(d)volume of section s2.
本文研究表明,多路段道路中,拥堵往往最先从路口开始,蔓延到整个路段.随着车辆流入概率的增大,路口的状态对交通流的影响也增大,出现了一种新的混合流现象.而且上一路段的拥堵,反而可能缓解下一路段的交通状况.从平均速度和平均车流密度的角度考虑,道路系统存在临界突变的特性.当车流流入概率小于阈值时,增加车辆数目不会影响整体的通行效率;当到达阈值时,车辆数目的缓慢增加也会迅速引起道路的拥堵.当车流量趋于饱和时,下游路段的车辆流入概率对道路整体通行能力影响更大.这些结论有利于更好地了解多路段道路的性质,也可用于指导交通的疏导和控制.例如,可以通过对实际道路的调查,进行仿真建模,得到临界车辆流入密度,用于防治拥堵.
多路段模型综合研究了多个路段的交通流特性,与传统模型相比,考虑了不同路段之间的影响,更加符合实际情况.而且模型的适用范围广,为多路段交通流的研究提供了一个基本的框架.在单路段交通流模型上的研究和进展,可以很好地迁移到多路段模型上来.但是,本文采用的单路段模型不够精细,对整体交通情况的仿真还不够贴近.另一方面,没有考虑车辆在路口附近行为的细节,与现实情况还存在一定差距.将来的研究工作需要进一步改进单路段模型,也需要更加细致地讨论路口的影响.
[1]Hua X D,Wang W,Wang H 2016Acta Phys.Sin.65 084503(in Chinese)[华雪东,王炜,王昊 2016物理学报65 084503]
[2]Wen J,Tian H H,Kang S J,Xue Y 2010Acta Phys.Sin.59 7693(in Chinese)[温坚,田欢欢,康三军,薛郁2010物理学报59 7693]
[3]Nagatani T 2015Physica A419 1
[4]Gao Y,Liu Y,Hu H,Ge Y 2016J.Adv.Transport.50 1470
[5]Tang T Q,Shi W F,Yang X B,Wang Y P,Lu G Q 2013Physica A392 6300
[6]Qian Y S,Feng X,Zeng J W 2017Physica A479 509
[7]Hua X D,Wang W,Wang H 2011Acta Phys.Sin.60 084502(in Chinese)[华雪东,王炜,王昊 2011物理学报60 084502]
[8]Jing M,Deng W,Wang H,Ji Y J 2012Acta Phys.Sin.61 244502(in Chinese)[敬明,邓卫,王昊,季彦婕2012物理学报61 244502]
[9]Zhang B,Zhao H Y 2016J.Kunming Univ.Sci.Technol.(Natural Science Edition)4 45(in Chinese)[张博,赵慧英2016昆明理工大学学报自然科学版4 45]
[10]Tang T Q,He J,Yang S C,Shang H Y 2014Physica A413 583
[11]Tang T Q,Lou C,Wu Y H,Huang H J,Yang X B 2014J.Adv.Transport.48 304
[12]Lakouari N,Bentaleb K,Ez-Zahraouy H,Benyoussef A 2015Physica A439 132
[13]Nagel K,Schreckenberg M 1992J.Phys.I France2 2221
[14]Fukui M,Ishibashi Y 1996J.Phys.Soc.Jpn.65 1868
[15]Wang L,Wang B H,Xu B M,Hu B B 2000Acta Phys.Sin.49 1926(in Chinese)[王雷,汪秉宏,许伯铭,胡斑比2000物理学报49 1926]
[16]Lei L,Xue Y,Dai S Q 2003Acta Phys.Sin.52 2121(in Chinese)[雷丽,薛郁,戴世强 2003物理学报52 2121]
[17]Peng L J,Kang R 2009Acta Phys.Sin.58 830(in Chinese)[彭莉娟,康瑞 2009物理学报 58 830]
[18]Zhang N X,Zhu H B,Lin H,Huang M Y 2015Acta Phys.Sin.64 024501(in Chinese)[张柠溪,祝会兵,林亨,黄梦圆2015物理学报64 024501]
[19]Lárraga M E,Luis A I 2014Chin.Phys.B23 057101
[20]Chen Q,Wang Y 2016J.Adv.Transport.50 949
[21]Zhao H T,Yang S,Chen X X 2016Physica A462 1301
[22]Qiu X P,Ma L N,Zhou X X,Yang D 2016J.Transport.Syst.Engineer.Inform.Technol.16 101(in Chinese)[邱小平,马丽娜,周小霞,杨达2016交通运输系统工程与信息16 101]
[23]Qiu X P,Yu D,Sun R X,Yang D 2016Appl.Res.Comput.33 2611(in Chinese)[邱小平,于丹,孙若晓,杨达2016计算机应用研究33 2611]
[24]Bouadi M,Jetto K,Benyoussef A,Kenz A E 2017Physica A469 1
[25]Zhang X Q,Wang Y,Hu Q H 2014Acta Phys.Sin.63 010508(in Chinese)[张兴强,汪滢,胡庆华2014物理学报63 010508]
[26]Zhao H T,Mao H Y 2013Acta Phys.Sin.62 060501(in Chinese)[赵韩涛,毛宏燕 2013物理学报 62 060501]
[27]Dong L Y,Xue Y,Dai S Q 2002Appl.Math.Mech.23 331(in Chinese)[董力耘,薛郁,戴世强 2002应用数学和力学23 331]
[28]Ge H X,Meng X P,Zhu H B,Li Z P 2014Physica A408 28
[29]Gipps P G 1981TransportationResearchPartB Methodological15 105
[30]Tan H L,Liu M R,Kong L J 2002Acta Phys.Sin.51 2713(in Chinese)[谭惠丽,刘慕仁,孔令江2002物理学报51 2713]
[31]Peng L,Tian H L,Kong L J,Liu M R 2003Acta Phys.Sin.52 3007(in Chinese)[彭麟,谭惠丽,孔令江,刘慕仁2003物理学报52 3007]
[32]Kerner B S,Rehborn H 1996Phy.Rev.E53 4275
Multi-section cellular automata model of traffic fl ow∗
Liang Jing-Yun1)Zhang Li-Li1)Luan Xi-Dao2)†Guo Jin-Lin1)Lao Song-Yang1)Xie Yu-Xiang1)
1)(School of Information System and Management,National University of Defense Technology,Changsha 410072,China)
2)(School of Computer Engineering and Applied Mathematics,Changsha University,Changsha 410022,China)
It is more common for drivers to pass through multiple sections to reach destinations instead of single road section.Howerver,most of researches concentrate on improving the e ff ect in an independent section.Based on traditional cellular automata traffic model,a multi-section model is proposed by regarding serverl road sections as a traffic system.In this model,di ff erent sections of the road might have di ff erent lengths,numbers of lanes or maximal speeds.And vehicles travel from one section to another.The main difficulty lies in dealing with the relationships among the traffic fl ows of di ff erent sections.Besides basic rules in NaSch model,the vehicle in flow rule,crossroad randomization brake rule and crossroad in flow rule is added in this paper to enable vehicles to flow between sections.At the beginning of section,to avoid con fl icting at crossroads under open boundary condition,the concept of car pool is introduced when new vehicles enter into sections.Before arriving at the end of section,crossroad randomization brake is used to simulate the in fl uences of crossroads.Speed decreases in probability until lower than a maximal crossroad speed.When leaving the section,vehicles go to the next section with a straight ratio.Also,new vehicles may enter according to traffic condition.Therefore,cellular automata of di ff erent sections can be connected in series.Finally,numerical simulation is demonstrated to study the in fl uences of important parameters,including traffic in flow probability,maximal crossroad speed and crossroad randomization brake probability.Compared with traditional models,this model focuses on connecting sections.And improvements of basic models can be implanted easily,thereby increasing the accuracy of the whole model in the future.
The experimental result are as follows.1)According to space-time graphs of di ff erent in flow probabilities,there is a new kind of traffic flow called mixed fl ow.Traffic congestion often starts from crossroads,and spreads to the whole section.And traffic jams in previous section might relieve traffic pressure in latter section.2)With the increase of traffic in flow probability,crossroads tends to have a greater in fl uence on average speed as well as average traffic density.What is more,the moderate increase of vehicle numbers could cause the road capacity to drop rapidly if it exceeds the threshold value.
multi-sections road,traffic fl ow,cellular automata,microscopic simulation
27 May 2017;revised manuscript
18 August 2017)
(2017年5月27日收到;2017年8月18日收到修改稿)
10.7498/aps.66.194501
∗国家自然科学基金(批准号:61571453)、湖南省自然科学基金(批准号:14JJ3010)和湖南省教育厅重点项目(批准号:15A020)资助的课题.
†通信作者.E-mail:xidaoluan@ccsu.cn
©2017中国物理学会Chinese Physical Society
PACS:45.70.Vn,89.40.–a
10.7498/aps.66.194501
*Project supported by the National Natural Science Foundation of China(Grant No.61571453),the Natural Science Foundation of Hunan Province,China(Grant No.14JJ3010),and the Research Foundation of Education Bureau of Hunan Province,China(Grant No.15A020).
†Corresponding author.E-mail:xidaoluan@ccsu.cn

