永磁同步风力发电机随机分岔现象的全局分析∗

杨黎晖 葛扬 马西奎

(西安交通大学电气工程学院,电力设备电气绝缘国家重点实验室,西安 710049)

永磁同步风力发电机随机分岔现象的全局分析∗

杨黎晖†葛扬 马西奎

(西安交通大学电气工程学院,电力设备电气绝缘国家重点实验室,西安 710049)

永磁同步风力发电机在运行过程中不可避免地会受到风能的随机干扰,本文建立了在输入机械转矩存在随机干扰情况下永磁同步风力发电机的数学模型,采用胞映射方法分析了随机干扰强度变化时系统全局结构的演化行为,并通过数值模拟对理论分析进行验证.研究结果表明,随着随机干扰强度的增大,系统中会出现随机内部激变和随机边界激变,即由于随机吸引子与其吸引域内的随机鞍发生碰撞而产生的随机分岔现象和由于随机吸引子与其吸引域边界发生碰撞而产生的随机分岔现象.研究结果揭示了随机干扰对永磁同步风力发电机运行性能影响的机理,为永磁同步风力发电系统的运行和设计提供了理论依据.

永磁同步风力发电机,随机分岔,非线性,胞映射

1 引 言

近年来风力发电快速发展,永磁同步发电机作为主流机型在风力发电领域中被广泛应用,因此对永磁同步发电机稳定性和可靠性的研究受到了人们的广泛关注.永磁同步电机是一个强非线性系统,其中必然会存在丰富的非线性动力学行为.近几年来,国内外许多文献应用非线性动力学理论和方法对永磁同步电机进行了深入研究［1−9］.文献［1,2］发现在某些参数及工作条件下永磁同步电机中会出现Hopf分岔和混沌现象,从而导致电机振荡失稳.文献［3］发现倍周期分岔是永磁同步电机进入混沌的途径之一.文献［4］给出了预测永磁同步电机发生混沌的参数空间,为系统的参数和控制器设计提供了理论参考.文献［5—9］发现用于风力发电的直驱永磁同步风力发电机中也会出现混沌现象,从而导致系统发生“无序”振荡.上述研究工作揭示了永磁同步电机失稳的动力学机理,为其设计和优化提供了理论基础.但是,这些研究工作都是在确定性系统理论的范围内进行的,而实际上永磁同步电机应用于风力发电时,在运行过程中不可避免地会受到风能的随机干扰.随机干扰可能引起发电机强烈的非线性随机振荡、失稳甚至崩溃.随机干扰对永磁同步风力发电机动力学行为的影响将直接关系到对其稳定工作范围的正确评估,是一个不能忽略的实际问题.因此,研究永磁同步风力发电机在随机干扰下的动力学行为,特别是全局动力学性态是使其安全可靠运行的重要保证.然而,目前尚未见到关于永磁同步风力发电机随机动力学行为的研究报道.

为了对随机动力系统全局的拓扑性质进行分析,就需要对系统进行相空间结构分析.为了克服直接数值模拟法对系统全局分析时效率低、存在有限步截断问题的不足,Hsu［10］在20世纪80年代提出了胞映射方法,该方法一步转移矩阵决定了相空间的最终性态,无时间截断,是一种对随机系统进行全局分析的有效工具［11］.近年来,在最早提出的简单胞映射方法的基础上发展形成了多种改进方法［12−15］,胞映射方法的理论已逐渐成熟.目前,已有文献采用胞映射方法对非线性系统的随机动力学行为进行全局分析,但大多是针对一些经典模型［16−18］,将其应用于分析实际系统的研究工作并不多见.

本文考虑风能的随机性对永磁同步风力发电机全局动力学特性的影响,在建立永磁同步风力发电机非线性随机模型的基础上,将胞映射方法应用于该系统非线性随机动力学行为的研究,分析随机干扰作用下系统全局结构性态的演化,给出系统中随机分岔的发生和发展过程,揭示随机干扰对永磁同步风力发电机运行性能影响的动力学机理.

2 随机输入转矩作用下永磁同步风力发电机的数学模型

直驱式永磁同步风力发电机组的基本结构如图1所示,机组由风力机、永磁同步电机、电力电子变换器及其控制器组成.风力机在风能的作用下旋转并带动永磁同步发电机转动,当达到切入风速后永磁同步发电机将机械能转化为电能并通过电力电子变换器将符合电网频率和电压要求的电能馈入电网.为了简化分析,忽略电力电子变换器及其控制器的动态过程,得到在转子磁场定向坐标系(d-q坐标系)下永磁同步风力发电机的动态方程为

其中,isd,isq和Usd,Usq分别为定子电流和定子电压的d轴和q轴分量;Rs为定子电阻;Lsd和Lsq分别为d轴和q轴电感,ψr为转子磁链,ωr为发电机转子转速,Tm为机械转矩,J为发电机的转动惯量,β为黏性阻尼系数,np为转子极对数.

假定发电机气隙均匀,则Lsd=Lsq,通过仿射和时间变换［1］,可得(1)式的无量纲状态方程为

风能的随机波动会引起永磁同步风力发电机的机械转矩呈随机变化.考虑风能的随机性,永磁同步风力发电机在随机输入转矩作用下的数学模型为

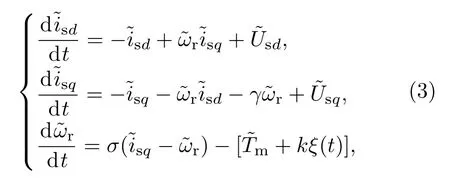
式中,ξ(t)为标准高斯过程,k为随机强度.因为在较短的时间内,转矩是围绕某一个均值波动的,所以这种波动在一般情况下可以近似为高斯过程.

3 随机输入转矩作用下永磁同步风力发电机的随机分岔

3.1 随机分岔的定义

随机干扰导致的系统定性性态的变化称为随机分岔.对于随机分岔的研究尚处于起步阶段,其理论体系尚不完善,缺少严格的一般性定理与准则.目前,描述随机分岔的方式主要有三类:系统稳态概率密度形状的突变(P-分岔)［19］,系统最大Lyapunov指数符号的变化(D-分岔)［19］和系统随机吸引子(或随机鞍)形态的突变［16］.其中,第三类定义可以表征在随机干扰作用下随机系统的全局拓扑性质变化,并且能够描述具有多吸引子的系统在随机激励作用下动力学特性的变化,而前两类随机分岔的定义对此几乎无法讨论［11］.因此,针对永磁同步风力发电机的系统特征和进行全局分析的要求,本文基于系统随机吸引子(或随机鞍)形态(包括尺寸、周期)的突变这一定义进行随机分岔分析.

3.2 胞映射方法

胞映射的基本思想是把动力系统的状态空间离散化为大量状态胞的集合,系统中状态的转移对应胞与胞的转移,通过对胞之间转移关系的研究来描述原系统的动力学行为［11］.在众多版本的胞映射方法中,广义胞映射图论方法因具有显著优点而被认为是一种用于研究随机动力系统的有效工具.特别是该方法可以得到动力系统的不稳定解集(鞍),这是其他方法不易得到的.为了更全面地反映永磁同步风力发电机的随机动力学全局特性,本文采用广义胞映射图论方法作为基本胞映射方法.由于本文研究的永磁同步风力发电机的模型为3阶,因此为了降低需要计算的胞空间的维数、减小计算量,在进行胞映射数值计算之前,先采用Poincarè型胞映射方法［20］将系统转化为Poincarè截面上的点映射系统,再求出系统在Poincarè截面上的胞映射关系.在分析多吸引子共存的情况时,由于系统的全局特性较复杂,为了既能准确反映系统的复杂空间结构又能提高计算效率,本文采用基于复合胞化空间的迭代方法［21］,根据状态空间的不同采用不同尺度的胞化方案,以得到更精细的胞映射动力系统.本文胞映射算法实现的主要过程为:

1)选取合适的Poincarè截面Σ, 将(3)式转化为Poincarè截面Σ上的点映射系统x(n+1)=g(x(n)),其中

2)在Poincarè截面Σ上选取研究范围R,R为二维平面,在R内分别沿坐标轴x1和x2划分为间距分别为h1和h2的N维胞状态空间,记为Γ={z1,z2,···,zN},其中zi为胞状态空间中的胞元素;

3)在每个胞内取M个采样点,对每个点记其坐标为(x1j,x2j),以每个点为初值,经过映射g后的像点为根据每个胞内采样点和其像点的关系,求出每个胞的像胞及一步转移概率pij.pij构成转移概率矩阵P,用pj(n)表示系统在第n步映射中位于胞j的概率,p(n)是以pj(n)为元素的N维矢量,则得到广义胞映射关系p(n+1)=P·p(n);

4)将每个胞对应于有向图的一个顶点,若两个胞之间存在一步可达关系,则在相应的顶点之间建立一条有向边,从而根据P建立有向图D=(V,E),其中V表示顶点集合,E表示有向边的集合;

5)对形成的有向图D=(V,E)进行分析得到强联通子图,根据强联通子图的特征得到系统的吸引子、吸引域、鞍和吸引域边界等信息;

6)若所分析的全局特性较复杂,则适当选取需要精细分割的胞状态集合Γ1,对Γ1进行细分为n1×n2的复合胞化空间.根据上述方法生成有向图D′=(V′,E′),并对其进行强联通分析以得到相应的结果;

7)如有必要,返回6),否则停止.

在分析多吸引子共存的系统的全局特性时,判断每个吸引子的稳定裕度是十分必要的.本文采用广义胞映射中保护层厚度这个概念来定量刻画吸引子被其吸引域保护的程度,即可反映吸引子的稳定裕度.通过比较保护层厚度这个值的大小来判断在多个吸引子共存的系统中随着随机强度的增加,哪个吸引子将会首先消失.第i个永久族(吸引子)的保护层厚度的定义为［22］

它表示第i个永久族集合A(i)与多驻处胞集合(吸引域边界)B(i,j)之间的距离.

3.3 随机内部激变

图2 (网刊彩色)参数选取sd=−75,sq=−15,m=−50时,随着随机强度k的变化永磁同步风力发电机全局性态的变化情况(红色区域为吸引子A(1),灰色区域为A(1)的吸引域B(1),蓝色区域为鞍S(1)) (a)k=0;(b)k=0.11;(c)k=0.12;(d)k=0.13;(e)k=0.14;(f)k=0.15Fig.2.(color online)The changes in global character of the permanent magnet synchronous generator with the variations of the stochastic intensity k,when the parameters are set assd=−75,sq=−15,m=−50(the attractor A(1)is marked as red area,its attraction basin B(1)is marked as gray area,the saddle S(1)is marked as blue area):(a)k=0;(b)k=0.11;(c)k=0.12;(d)k=0.13;(e)k=0.14;(f)k=0.15.

当k=0时,即输入机械转矩不存在随机扰动时永磁同步风力发电机的全局性态如图2(a)所示.此时,系统有1个吸引子A(1)和1个鞍S(1),且鞍存在于吸引子的吸引域B(1)内部.考虑随机强度k的变化对永磁同步风力发电机全局特性产生的影响.随着随机强度k的增大,随机吸引子和随机鞍变大.当k=0.11时,系统的全局特性如图2(b)所示,随机吸引子逐渐伸向随机鞍,其指端即将接触到随机鞍的右上半支.进一步增大k,当k=0.12时,随机吸引子与随机鞍发生碰撞,导致随机鞍的右上半支消失,成为随机吸引子的一部分,吸引子的形态发生突变,系统发生了随机分岔,如图2(c)所示.继续增大随机强度,随机吸引子再次逐渐靠近随机鞍的右下半支和左半支,如图2(d)和图2(e)所示.当随机强度k由0.14增至0.15时,随机吸引子与随机鞍再次发生碰撞,随机鞍突然消失并成为随机吸引子的一部分,在关心的区域内仅有一个大的随机吸引子,如图2(f)所示.此时鞍变为吸引子,吸引子的几何空间体积突然增大,形态发生了突变,系统再次发生随机分岔.表1给出了随着随机强度k的变化,系统的吸引子和鞍的胞的变化情况.这种随机分岔实际上是一种由于随机吸引子与其吸引域内的随机鞍发生碰撞而产生的随机激变现象,即随机内部激变［24］.

由上述永磁同步风力发电机全局性态的变化可以看出,当输入转矩存在较小强度的随机扰动时,永磁同步风力发电机会围绕一个稳定运行点做小幅的随机振荡,随着随机强度的增大,随机吸引子的胞数增多,以致随机振荡的幅值也会增大.当随机吸引子与随机鞍首次碰撞而发生随机分岔时,随机吸引子胞数的突增导致永磁同步风力发电机会突然发生更为明显的随机振荡.当随机吸引子与随机鞍再次碰撞,随机鞍突然消失,随机吸引子形态突变,系统再次发生随机分岔时,永磁同步风力发电机将突然剧烈、无序地振荡,甚至发电机的转速r会出现负值,系统失去稳定性.可见,随机扰动强度增大而引起的随机内部激变是导致永磁同步风力发电机失稳的动力学本质.

表1 随着随机强度k的变化吸引子和鞍的胞数目的变化情况Table 1.The changes in the number of the attractor and saddle with the variations of the stochastic intensity k.

3.4 随机边界激变

当k=0时,即不存在随机扰动时永磁同步风力发电机的全局性态如图3(a)所示.此时,系统有2个共存的吸引子A(1)和A(2),2个吸引子对应的2个吸引域B(1)和B(2)的交界处存在多驻处胞,即吸引域边界B(1,2).根据(4)式可计算出吸引子A(1)的保护层厚度为d1=18.35,吸引子A(2)的保护层厚度为d2=310.82.由于d1＜d2,因此可预判随着随机强度的增大,吸引子A(1)将会首先消失.

考虑随机强度k的变化对永磁同步风力发电机全局特性产生的影响.随着随机强度k的增大,2个随机吸引子和吸引域边界都逐渐增大,如图3(b)所示.当k=0.0033时,系统的全局特性如图3(c)所示,随机吸引子A(1)逐渐伸向吸引域边界,其指端即将接触到吸引域边界.进一步增大k,当k=0.0034时,随机吸引子A(1)与吸引域边界B(1,2)发生碰撞,该吸引子连同其吸引域及吸引域边界消失,而在消失的吸引子的位置上出现了一个随机鞍S(1),此时在研究的区域内系统仅存在一个随机吸引子A(2).由于吸引子的数量和性质都发生了突变,系统发生随机分岔,如图3(d)所示.这里验证了前面得到的结论,即当随机强度增大到一定程度时,随机吸引子A(1)首先消失.表2给出了随着随机强度的变化,系统的吸引子和鞍的胞数的变化情况.上述随机分岔是一种由于随机吸引子与其吸引域边界发生碰撞而产生的随机激变现象,即随机边界激变［24］.

由上述永磁同步风力发电机全局性态的变化可以看出,当输入转矩中的随机扰动强度较小时,永磁同步风力发电机会围绕一个稳定运行点做小幅的随机振荡,随着随机强度的增大,随机振荡的幅值逐渐增大,且对该稳定工作点起到保护作用的吸引域边界也在增大,导致随机振荡的范围逐渐靠近吸引域边界,系统的稳定裕度变小.当此随机吸引子与其吸引域边界碰撞而发生随机分岔后,原来的稳定解集(吸引子A(1))消失,取而代之的是不稳定解集(鞍S(1)),在研究的区域内仅存在一个随机吸引子A(2).由于仅存的随机吸引子所对应的发电机转速为负,所以对于工程实际中的永磁同步风力发电机来说,发电机将发生运行的突然崩溃.可见,随机扰动强度增大而引起的随机外部激变是导致永磁同步风力发电机运行崩溃的动力学本质.

图3 (网刊彩色)参数选取sd=10,sq=−50,m=−55时,随着随机强度k的变化永磁同步风力发电机全局形态的变化情况(红色区域为吸引子A(1)和A(2),白色区域为A(1)的吸引域B(1),灰色区域为A(2)的吸引域B(2),绿色区域为吸引域边界B(1,2),蓝色区域为鞍S(1)) (a)k=0;(b)k=0.0025;(c)k=0.0033;(d)k=0.0034Fig.3.(color online)The changes in global character of the permanent magnet synchronous generator for wind turbine with the variations of the stochastic intensity k,when the parameters aresd=10,sq=−50,m=−55(the attractor A(1)and A(2)is marked as red area,the attraction basin B(1)of A(1)is marked as white area,the attraction basin B(2)of A(2)is marked as gray area,the boundary of the attraction basin B(1,2)is marked as green area,the saddle S(1)is marked as blue area):(a)k=0;(b)k=0.0025;(c)k=0.0033;(d)k=0.0034.

表2 随着随机强度k的变化,吸引子、鞍和吸引域边界的胞数目的变化情况Table 2.The changes in the number of the attractor,saddle and boundary of the attraction basin with the variations of the stochastic intensity k.

4 数值模拟

为了更直观地描述第3节中所分析的永磁同步风力发电机的随机分岔现象,并验证采用胞映射方法得到的分析结果的正确性,本节采用Euler-Maruyama(EM)方法对随机输入转矩作用下永磁同步风力发电机的随机响应进行数值模拟.从统计学角度来看,用EM方法求解随机微分方程组时,每一条维纳过程路径上的解过程可以看成是总体中的一个抽样样本.为了阐释数值模拟的结果,本节中分别给出仿真结束时刻发电机转速的分布直方图［25］(仿真结束时刻转速的所有随机路径在不同转速区间的个数)以描述转速的分布情况;转速的样本均值［25］曲线(所有随机路径上解过程的平均值)、第一四分位数和第三四分位数［25］曲线(每个时刻所有随机路径的数据排序后处于25%和75%位置上的值所构成的曲线)以描述随机响应的波动情况;某一随机路径的时域波形图.

4.1 随机内部激变

永磁同步风力发电机参数γ和σ、定子电压sd和sq以及机械转矩m的取值与3.3节相同,仿真时间50 s,取2000个随机路径,初值取在吸引子A(1)附近,为当随机强度k=0.1,系统未发生随机分岔时,发电机转速的随机响应数值模拟结果如图4所示.可以看出,发电机的转速分布于13.9—14.7之间,风力发电机围绕r=14.29的平衡点以较小幅度平缓地随机波动,处于稳定运行状态.

当随机强度k=0.5,系统发生随机内部激变后,发电机转速的随机响应情况如图5所示.可以看出,与图4相比发电机转速的随机振荡幅值明显增大,分布于−20—30之间,在剧烈振荡过程中转速出现负值,实际系统无法正常运行,失去稳定性.与图2对比可以看出,发生随机分岔后转速的分布与图2(f)中吸引子所覆盖的转速范围相同.图5所示的失稳现象正是由于随机吸引子与其吸引域内的随机鞍发生碰撞导致随机鞍消失、随机吸引子的几何空间体积突然增大而引起的.

图4 参数选取sd=−75,sq=−15,m=−50,系统稳定时永磁同步风力发电机转速的随机响应(a)t=50 s时在2000条路径上的分布直方图;(b)在2000条路径上解过程的样本均值(Mean)曲线、第一四分位数(Q1)和第三四分位数(Q3)曲线;(c)某一随机路径的时域波形Fig.4.The stochastic responses of the rotor speed of the permanent magnet synchronous generator for wind turbine when the system is stable,with the parameterssd=−75,sq=−15,m=−50:(a)The histogram at t=50 s over 2000 trajectories;(b)the mean and the fi rst-third quartile quartiles over 2000 trajectories;(c)the waveform of one sample trajectory.

4.2 随机边界激变

发电机参数γ和σ、定子电压sd和sq以及机械转矩m的取值与3.4节相同,仿真时间为50 s,取10000个随机路径,初值设在吸引子A(1)的吸引域B(1)内,为当随机强度k=0.0025,系统未发生随机分岔时,发电机转速的随机响应情况如图6所示.可以看出,由于初值设在吸引子A(1)的吸引域内,因此发电机围绕r=8.07的平衡点以较小幅度随机振荡,转速的振荡幅值在7.85—8.3之间,永磁同步风力发电机处于稳定运行状态.

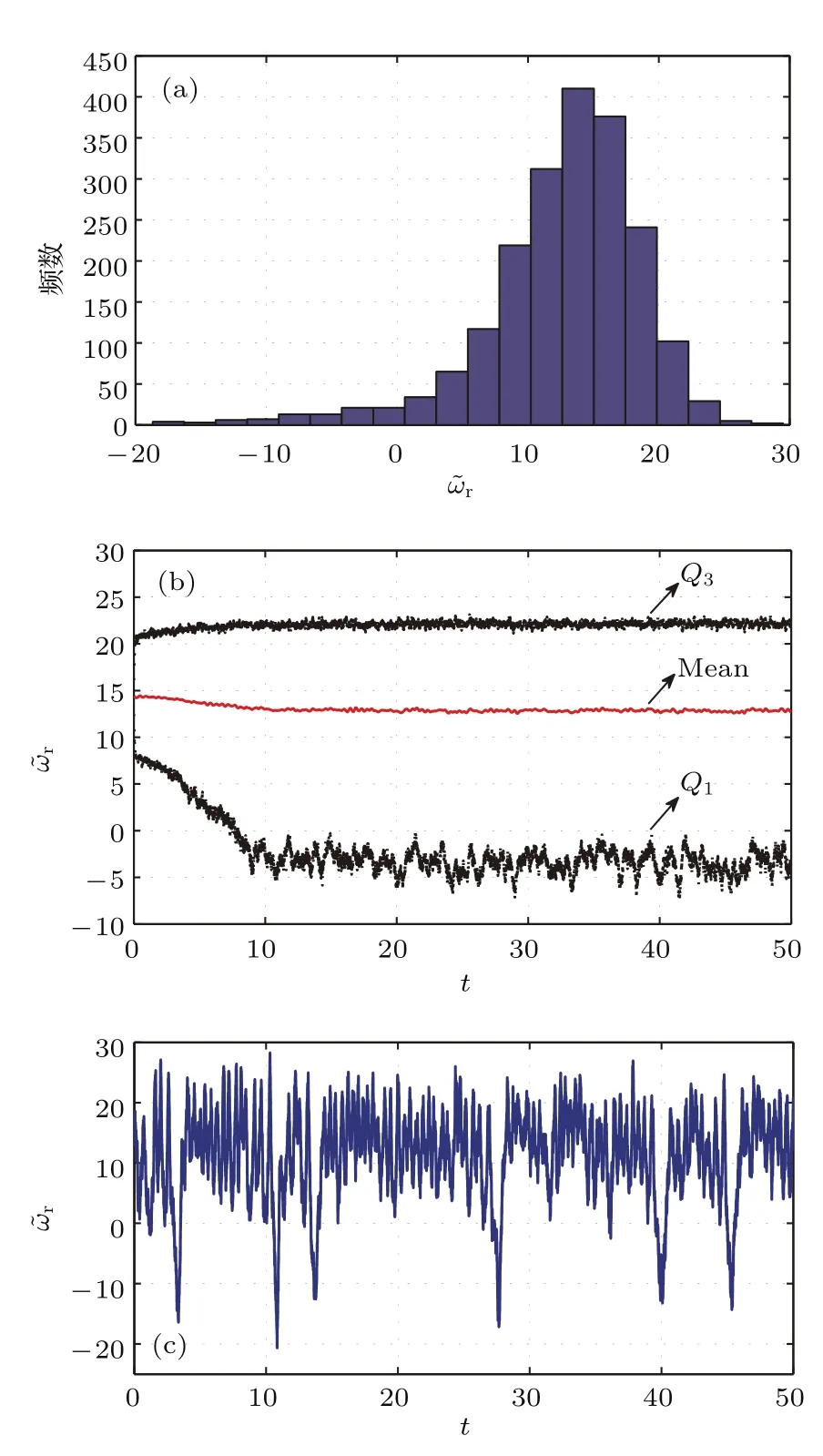
图5 参数选取sd=−75,sq=−15,m=−50,发生随机分岔后永磁同步风力发电机转速的随机响应 (a)t=50 s时在2000条路径上的分布直方图;(b)在2000条路径上解过程的样本均值(Mean)曲线、第一四分位数(Q1)和第三四分位数(Q3)曲线;(c)某一随机路径的时域波形Fig.5.The stochastic responses of the rotor speed of the permanent magnet synchronous generator for wind turbine after the stochastic bifurcation happens,with the parameterssd=−75,sq=−15,m=−50:(a)The histogram at t=50 s over 2000 trajectories;(b)the mean and the fi rst-third quartile quartiles over 2000 trajectories;(c)the waveform of one sample trajectory.

图6 参数选取sd=10,sq=−50,m=−55,系统稳定时永磁同步风力发电机转速的随机响应 (a)t=50 s时在10000条路径上的分布直方图;(b)在10000条路径上解过程的样本均值(Mean)曲线、第一四分位数(Q1)和第三四分位数(Q3)曲线;(c)某一随机路径的时域波形Fig.6.The stochastic responses of the rotor speed of the permanent magnet synchronous generator for wind turbine when the system is stable,with the parameterssd=10,sq=−50,m=−55:(a)The histogram at t=50 s over 10000 trajectories;(b)the mean and the fi rst-third quartile quartiles over 10000 trajectories;(c)the waveform of one sample trajectory.

当随机强度k=0.015,系统发生随机边界激变后,发电机转速的随机响应情况如图7所示.可见,当t=50 s时发电机转速r在10000条路径上的分布直方图出现了双峰,转速的样本均值曲线不断下降.具体到某一随机路径,发电机在运行一段时间后,转速突然降为负值,实际系统失稳崩溃.与图3对比可以看出,转速分布直方图中两个双峰的中心r=8.07和r=−1.44,分别与图3(a)中吸引子A(1)和A(2)所对应的转速符合.当随机强度增大而导致随机吸引子A(1)与其吸引域边界碰撞而发生随机分岔后,原来的稳定解集(吸引子A(1))消失并变为不稳定解集(鞍S(1)),在研究的区域内仅存在一个随机吸引子A(2).由于数值模拟的初值设在原吸引子A(1)的吸引域内,即发生随机分岔后的鞍S(1)区域内,因此在运行一段时间后,发电机的运行状态被吸引子A(2)所吸引,以A(2)为平衡点做随机振荡.由于吸引子A(2)所对应的转速为负,因此永磁同步风力发电机的运行崩溃.

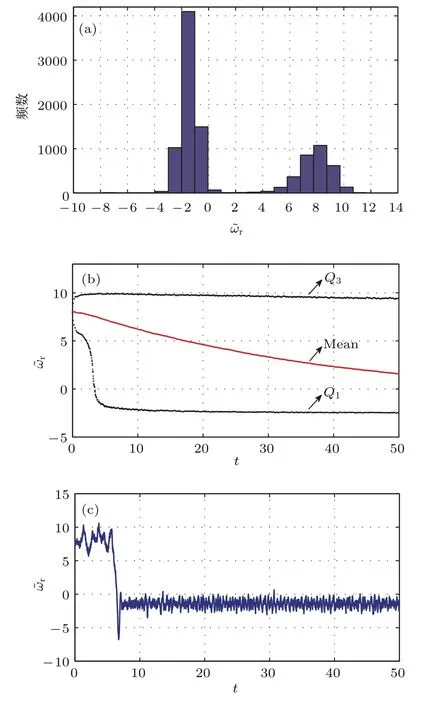
图7 参数选取sd=10,sq=−50,m=−55,发生随机分岔后永磁同步风力发电机转速的随机响应 (a)t=50 s时在10000条路径上的分布直方图;(b)在10000条路径上解过程的样本均值(Mean)曲线、第一四分位数(Q1)和第三四分位数(Q3)曲线;(c)某一随机样本的时域波形Fig.7.The stochastic responses of the rotor speed of the permanent magnet synchronous generator for wind turbine after the stochastic bifurcation happens,with the parameterssd=−75,sq=−15,m=−50:(a)The histogram at t=50 s over 10000 trajectories;(b)the mean and the fi rst-third quartile quartiles over 10000 trajectories;(c)the waveform of one sample trajectory.

4.3 结果讨论

需要说明的是,一方面,与确定性系统的分岔行为不同,由于受到随机因素的作用,随机系统即使满足一定的分岔条件也并非一定会发生随机分岔,而是具有发生分岔的可能.因此,第3节中采用胞映射法分析得到的永磁同步风力发电机发生分岔时随机强度的临界值仅能表示当随机强度大于临界值时系统发生随机分岔的概率较大.其意义在于可指导系统的运行和设计从而降低发生随机分岔的概率,但无法通过此临界值对随机系统的分岔做出确定性的预测.

另一方面,由于对随机响应的直接数值模拟需要计算大量样本轨线的长期行为才能得到更精确的结果,而受到计算机计算能力的限制,总是对有限的样本进行有限步截断,因此直接数值模拟得到的结果必然存在误差.

综上,本节对随机响应的数值模拟验证了永磁同步风力发电机中随机内部激变和随机边界激变的存在性.然而,由于随机系统的复杂性和直接数值模拟法的不足,无法对发生随机分岔时的随机强度临界值进行准确的验证.

5 结 论

本文针对风能的随机性,建立了在输入机械转矩存在随机干扰情况下永磁同步风力发电机的非线性随机模型,采用胞映射方法分析了随机干扰强度变化时系统全局结构的变化过程及出现的随机分岔现象,并通过对系统的随机响应进行数值模拟验证了理论分析的正确性.研究结果表明,随着随机干扰强度的增大,系统中出现了两种随机分岔现象:

1)当随机强度增至临界值时,随机吸引子与其吸引域内的随机鞍发生碰撞,导致随机鞍突然消失、随机吸引子的几何空间体积突增、形态发生突变,在此变化过程中,永磁同步风力发电机发生强烈的随机振荡并最终失去稳定性;

2)当随机强度增至临界值时,一个随机吸引子与其吸引域边界发生碰撞,该吸引子连同其吸引域及吸引域边界消失,在原吸引子的位置上出现了一个随机鞍,系统吸引子的数量发生了突变,在此变化过程中,永磁同步风力发电机的随机振荡幅值不断增大,最终由于稳定解集的消失,系统失稳崩溃.

总之,小强度的随机干扰就会导致系统稳定性结构的完全破坏,使原本处于稳定状态的系统发生强烈的无序振荡和运行崩溃.因此,本文研究随机干扰对系统动力学行为演化的影响对于系统的安全可靠运行具有重要的指导意义.

［1］Zhang B,Li Z,Mao Z Y,Pang M X 2001Proc.CSEE21 13(in Chinese)［张波,李忠,毛宗源,庞敏熙2001中国电机工程学报21 13］

［2］Xue W,Guo Y L,Chen Z Q 2009Acta Phys.Sin.58 8146(in Chinese)［薛薇,郭彦岭,陈增强 2009物理学报58 8146］

［3］Wei D Q,Luo X S,Fang J Q,Wang B H 2006Acta Phys.Sin.55 54(in Chinese)［韦笃取,罗晓曙,方锦清,汪秉宏2006物理学报55 54］

［4］Rasoolzadeh A,Tavazoei M S 2012Phys.Lett.A377 73

［5］Yang G L,Li H G 2009Acta Phys.Sin.58 7552(in Chinese)［杨国良,李惠光 2009物理学报 58 7552］

［6］Zheng G,Zou J X,Xu H B,Qin G 2011Acta Phys.Sin.60 060506(in Chinese)［郑刚,邹见效,徐红兵,秦钢2011物理学报60 060506］

［7］Wang L,Li Y H,Lu G L,Zhu X H 2011Electric Power Automation Equipment31 45(in Chinese)［王磊, 李颖晖,逯国亮,朱喜华2011电力自动化设备31 45］

［8］Ren L N,Liu F C,Jiao X H,Li J Y 2012Acta Phys.Sin.61 060506(in Chinese)［任丽娜,刘福才,焦晓红,李俊义2012物理学报61 060506］

［9］Messadi M,Mellit A,Kemih K,Ghanes M 2015Chin.Phys.B24 010502

［10］Hsu C S 1980J.Appl.Mech.47 931

［11］Xu W 2013Numerical Analysis Methods for Stochastic Dynamical System(Beijing:Science Press)p43(in Chinese)［徐伟2013非线性随机动力学的若干数值方法及应用(北京:科学出版社)第43页］

［12］Hsu C S 1981J.Appl.Mech.48 634

［13］Tongue B H,Gu K 1988J.Sound Vib.125 169

［14］Jiang J,Xu J X 1994Phys.Lett.A188 137

［15］Hsu C S 1995Int.J.Bifurcat.Chaos5 1085

［16］Xu W,He Q,Rong H W,Fang T 2003Acta Phys.Sin.52 1365(in Chinese)［徐伟,贺群,戎海武,方同 2003物理学报52 1365］

［17］Xu W,Yue X L 2010Sci.China:Technol.Sci.53 664

［18］Li Z G,Jiang J,Hong L 2015Int.J.Bifurcat.Chaos25 1550109

［19］Arnold L 1998Random Dynamical Systems(Berlin,Heidelberg,New York:Springer)pp34–35

［20］Levitas J,Weller T,Singer J 1994J.Sound Vib.176 641

［21］He Q,Xu W,Li S,Xiao Y Z 2008Acta Phys.Sin.57 4021(in Chinese)［贺群,徐伟,李爽,肖玉柱 2008物理学报57 4021］

［22］Gong P L,Xu J X 1998Appl.Math.Mech.19 1087(in Chinese)［龚璞林,徐健学1998应用数学和力学19 1087］

［23］Zhu W Q,Yu J S 1987J.Sound Vib.117 421

［24］Hong L,Xu J X 2002Acta Phys.Sin.51 2694(in Chinese)［洪灵,徐健学 2002物理学报 51 2694］

［25］Guan Y H 2009Statistics(Beijing:Higher Education Press)pp66–83(in Chinese)［管于华 2009统计学 (北京:高等教育出版社)第66—83页］

Global analysis of stochastic bifurcation in permanent magnet synchronous generator for wind turbine system∗

Yang Li-Hui†Ge Yang Ma Xi-Kui
(State Key Laboratory of Electrical Insulation and Power Equipment,School of Electrical Engineering,Xian Jiaotong University,Xi’an 710049,China)

The permanent magnet synchronous generator(PMSG)for wind turbine system operating under inevitable stochastic disturbance from wind power is a nonlinear stochastic dynamical system.With the random interaction and nonlinearity,the intense nonlinear stochastic oscillation is likely to happen in such a system,causing the system to be unstable or even collapse.However,the PMSG is usually considered as a deterministic system when analyzing its nonlinear dynamic behaviors in the past researches.Such a simpli fi cation can lead to wrong predictions for the system stability and reliability.This paper aims to discuss the e ff ect of the stochastic disturbance on the nonlinear dynamic behavior of the PMSG.Based on the derived PMSG model considering the stochastic disturbance from the input mechanical torque,the evolution of the system global structure with the stochastic intensity is investigated using the generalized cell mapping digraph method.Meanwhile,the occurrence process and development process of the stochastic bifurcation are illustrated.Based on this global analysis,the intrinsic mechanism for the e ff ect of the stochastic disturbance on the operating performances of the PMSG is revealed.Finally,the numerical simulations based on the Euler-Maruyama algorithm are carried out to validate the results of the theoretical analysis.The results present that as the intensity of the stochastic disturbance increases,two kinds of stochastic bifurcations can be observed in the PMSG system according to the de fi nition of a sudden change in characteristic of the stochastic attractor.One is the stochastic interior crisis that occurs when a stochastic attractor collides with a stochastic saddle in its attraction basin interior,leading to the abrupt increase of the attractor and the disappearance of the saddle.This kind of bifurcation results in the intense stochastic oscillation and instability of the PMSG system.Another stochastic bifurcation is the stochastic boundary crisis which occurs when a stochastic attractor collides with the boundary of its attraction basin and results in the disappearance of the attractor.This sudden change of the number of stochastic attractors induces the stable solution set to vanish and thus the PMSG system to collapse.In a word,even the stochastic disturbance with small intensity may lead to the complete destruction of the stable structure of the PMSG,inducing the system to su ff er a strong disordered oscillation or the operation to collapse.The results of this paper can provide signi fi cant theoretic reference for both practically operating and designing the PMSG for wind turbine systems.

permanent magnet synchronous generator,stochastic bifurcation,nonlinear,cell mapping

5 March 2017;revised manuscript

2 July 2017)

(2017年3月5日收到;2017年7月2日收到修改稿)

10.7498/aps.66.190501

∗国家自然科学基金(批准号:51207122)和陕西省自然科学基础研究计划(批准号:2016JQ5034)资助的课题.

†通信作者.E-mail:lihui.yang@mail.xjtu.edu.cn

©2017中国物理学会Chinese Physical Society

PACS:05.45.–a,88.50.G–

10.7498/aps.66.190501

*Project supported by National Natural Science Foundation of China(Grant No.51207122)and Natural Science Basic Research Plan in Shaanxi Province of China(Grant No.2016JQ5034).

†Corresponding author.E-mail:lihui.yang@mail.xjtu.edu.cn