新型干涉高光谱成像系统的光束剪切特性分析∗

李建欣 柏财勋 刘勤 沈燕 徐文辉 许逸轩

1)(南京理工大学电子工程与光电技术学院,南京 210094)

2)(南京理工大学,先进固体激光工业和信息化部重点实验室,南京 210094)

新型干涉高光谱成像系统的光束剪切特性分析∗

李建欣1)2)†柏财勋1)2)刘勤1)沈燕1)徐文辉1)许逸轩1)

1)(南京理工大学电子工程与光电技术学院,南京 210094)

2)(南京理工大学,先进固体激光工业和信息化部重点实验室,南京 210094)

提出了一种基于新型双折射横向剪切分束器的高光谱成像方法,采用的横向剪切分束器主要由Wollaston棱镜和角锥反射体组成.在分析双折射分束器的偏光结构和分光机理的基础上,利用光线追迹方法分析了光束在Wollaston棱镜中的传播特性,通过计算光束在双折射分束器中的传播方向及出射位置,推导出调制光程差的理论表达公式.根据理论推导结果,分别仿真分析了系统在不同扫描模式下光程差与入射光视场角以及角锥顶点偏移量的调制关系.基于理论分析结果搭建了实验装置,对光程差分析结果进行验证,实验结果与理论分析结果匹配较好.所提方法可以提高剪切光束的平行性,保证干涉条纹的高调制度,降低了复原光谱准确度对光学装调精度和元件加工精度的依赖性,具有结构稳定、复杂度低的显著特点.

光谱学,干涉,双折射,光程差

1 引 言

高光谱成像技术将成像技术与光谱探测技术结合在一起,可以同时获取探测目标的二维空间信息和精细光谱信息.得益于在可见光和红外波段的细分成像,该技术为物质的特性分析提供了一种有效的判定手段,在生物医疗、环境监测、精准农业、伪装识别、资源勘探、文物鉴定、刑事侦查、机器视觉和食品安全等领域具有很大的应用潜力.

干涉型高光谱成像技术由于其优异的光通量、光谱分辨率和空间分辨率特性,在众多的光谱成像技术中占有重要位置.目前的干涉型高光谱成像技术主要采用了Michelson［1−3］、Sagnac［4−9］、Mach-Zehnder［10］、Fabry-Pérot［11,12］干涉成像技术, 以及双折射偏振干涉成像技术［13−22］.其中双折射偏振干涉成像技术主要分为基于Wollaston棱镜的横向剪切干涉仪和基于Savart棱镜的横向剪切干涉仪,具有结构简单、体积紧凑的优点,在实际应用中具有很大潜力.英国Harvey和Fletcher-Holmes［15］提出了一种基于双Wollaston棱镜的干涉高光谱成像方法,系统中利用两片相同的Wollaston棱镜组成横向剪切分束器,凝视成像时通过扫描其中一片Wollaston棱镜实现对光束的连续干涉调制.国内西安交通大学李杰等［19］对基于双Wollaston棱镜的静态高光谱成像技术方案展开研究,同样利用两片相同的Wollaston棱镜组成横向剪切分束器,基于干涉光程差与光线入射角之间的调制关系,通过系统整体扫描实现对光束的连续干涉调制.另外,该系统还可以通过调整两片Wollaston棱镜的间距实现对光谱分辨率的调节.张淳民等［20,21］研究了一种基于Savart偏光镜的偏振干涉高光谱成像方法,利用Savart偏光镜的横向剪切特性,实现对光束的剪切干涉调制.通过单轴晶体组合的方法对Savart偏光镜的成像视场进行了优化设计,可以实现大视场高光谱成像探测.

双折射剪切分束器是高光谱成像系统的核心组件,需要保证它具有较高的加工精度和装调精度.但在双折射光学元件的实际加工和装调过程中,达到高精度要求具有一定难度.因此,当入射光束经过剪切分束器后,加工误差和装调误差会导致干涉条纹信号的混叠和调制度降低,影响光谱复原的精度.为得到高调制度的干涉信息,保证复原光谱信息的准确度,一方面需要提高光学元件的加工工艺水平,另一方面需要提高结构支撑精度和稳定性.然而,这两方面的技术途径却增加了系统的复杂度和制造成本.针对高光谱成像仪的复杂度和稳定性问题,本文提出一种新型双折射偏振干涉高光谱成像方法.将单个Wollaston棱镜和角锥反射体组合成横向剪切分束器［23］,由于角锥反射体具有严格的后向反射特性,即使Wollaston棱镜存在加工误差和装调误差,光束仍能够被严格地横向剪切为两束平行光并发生干涉,保证了干涉条纹的调制度,因此系统具有复杂度低、稳定性高的特点.在保证光谱复原精度的同时,通过降低加工和装调难度,可以减少仪器的制造成本.

2 双折射偏振干涉高光谱成像仪

新型双折射偏振干涉高光谱成像系统包括前置准直光学系统(L1,FS和L2),偏振分光棱镜(PBS),半波片(HP),Wollaston棱镜(WP),角锥反射体(R),成像物镜(L3)以及探测器(D),系统原理图如图1所示.某一视场角的光线经过前置准直光学系统进入偏振分光棱镜,透射光变为偏振方向平行于y轴的线偏振光.由于半波片的光轴与y轴之间存在夹角,透射线偏振光的偏振方向偏转后入射至Wollaston棱镜.Wollaston棱镜由两块光轴相互正交的晶体楔板组成,光轴分别平行于y轴与z轴,线偏振光在第一块楔板中分为振动方向互相正交的o光和e光,进入第二块楔板后,第一块楔板中的o光变为e光,反之亦然;从Wollaston棱镜出射的为两束偏振方向正交且具有一定分束角的oe光和eo光.随后两束线偏振光经角锥反射体按原方向反射回Wollaston棱镜,再次经过同一片Wollaston棱镜后,两束线偏振光的出射方向平行,且与光线入射系统时的方向相同.两束光线被横向剪切开一定距离,但此时两束光的偏振方向正交,再次经过半波片和偏振分光棱镜反射后,使得两束线偏振光具有相同的偏振方向.最终两束线偏振光经成像物镜成像在探测器靶面同一点上,并发生干涉.

目标上不同位置的物点对应着不同的视场角,而系统的调制光程差与视场角相关,因此像面上不同位置的像点对应着不同的调制光程差,所形成的像是经过光程差调制的干涉图像.系统在扫描成像过程中,每个像点在不同时刻被不同的光程差进行调制,经过完整的扫描后该像点形成干涉条纹.对该干涉条纹数据进行光谱反演,即可得到所对应物点的光谱信息.

干涉光强I(x)和光谱信息S(σ)存在以下傅里叶变换关系:

式中,σ为波数(σ=1/λ,λ为波长),x为光强的位置,L(σ,x)为波数σ的光束在位置x处的光程差.根据(1)式可知,光谱信息与光强信息以及调制光程差相关,其中光强信息可以通过探测器采集到的干涉图的像素灰度值获得,而调制光程差的确定则需要分析系统的光束剪切特性与系统参数间的关系.

图1 (网刊彩色)双折射偏振干涉高光谱成像系统Fig.1.(color online)Interferometric hyperspectral imager based on birefringence polarization interference.

3 光束剪切特性分析

3.1 光在单个Wollaston棱镜中的传播特性

光线在单轴晶体内的光程计算方法有两种:一是光线追迹法,光程为光线几何长度与光线方向折射率的乘积;二是光波法线追迹法,光程为光波法线几何长度与光波法线方向折射率的乘积.两种方法得到的光程计算结果相同,本文采用光线追迹法来精确计算光程差.

Wollaston棱镜由两块光轴相互正交的单轴负晶体楔板胶合而成,假设棱镜内部结构角为α,如图2(a)所示.视场角为θ的光线入射到Wollaston棱镜,在第一块晶体中分裂成振动方向互相垂直的两束线偏振光,eo光和oe光.在晶体I中,eo光偏振方向与光轴平行,为e光,方向与e光波法线方向一致,折射率为ne;oe光偏振方向与光轴垂直,为o光,折射率为no.入射空气介质的折射率为ni,由折射定律可得eo光与oe光与x轴的夹角βeo_I和βoe_I分别为

图2 (网刊彩色)(a)Wollaston棱镜中光的传播示意图;(b)e光波法线在晶体II中的传播示意图Fig.2.(color online)(a)The propagation of light in Wollaston prism;(b)the propagation of e-wave.

当光线从晶体I折射进入晶体II时,eo光由e光变为o光,折射率变为no,设eo光的光线方向与x轴的夹角为βeo_II,且折射角为则可求得βeo_II为

同时,oe光由o光变为e光,由于光线的波法线与光轴夹角与入射光线的视场角相关,所以oe光折射率随光的波法线方向变化.已知光轴与入射面的夹角为α,可求得oe光波法线的折射角为

由于oe光的光线方向与其波法线方向并不相同,结合图2(b)可知,oe光的波法线方向与光轴的夹角为且oe光光线方向与光轴的夹角为βoe_r,二者之间的关系为可求得oe光的光线方向与x轴的夹角βoe_II为

根据波法线之间的Snell定律,可知oe光波法线在晶体II中的折射率假设oe光的光线方向与波法线方向之间的离散角ψ=βoe_r−βoe_w,并且它与oe光折射率noe的关系为则oe光在晶体II中的折射率为

随后光线从Wollaston棱镜出射,进入空气介质.由折射定律可知,eo光和oe光与x轴的夹角ξeo和ξoe分别为

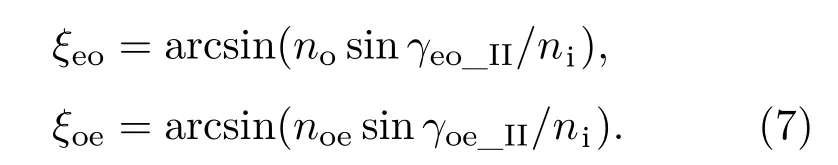
3.2 剪切平行性分析

角锥反射体是一种高精度光学元件,具有严格的后向反射特性.它的显著特点在于任意一条进入通光孔径的入射光线,无论入射角大小,光线经过角锥棱镜三个直角面反射后,都将按原方向从入射面反向出射.根据反射棱镜的等效作用与展开方法［24］,在角锥棱镜内,按照入射光线经过反射面的顺序,以反射面为对称面,依次使角锥棱镜镜像对称.以角锥棱镜的顶点O为坐标原点,以三条直角边OA,OB,OC所在的直线为x,y,z轴,建立如图3所示的坐标系.假设角锥的位置位于在三维坐标系O-xyz的第一象限,等效于三棱锥OABC,根据棱镜展开方法,三棱锥OABC分别以三个直角面作为对称面经过三次镜像对称后,位置位于第七象限,如图中三棱锥OA′B′C′所示.分析三棱锥OABC和三棱锥OA′B′C′的位置关系可知,二者关于坐标系原点(即角锥顶点)中心对称.最终,角锥反射体等效展开为平行平板,ABC所在平面为角锥等效平板的入射面,A′B′C′所在平面为角锥等效平板的出射面.分析光线在角锥内的传播特性时,可以等效地分析为光线在等效平板内传播.由于光线在等效平板出射面A′B′C′上的出射位置与在角锥实际出射面ABC的出射位置关于角锥顶点中心对称,可以容易地得出光线实际出射点坐标及出射方向.

由角锥棱镜与Wollaston棱镜组成剪切分束器,它的光束剪切平行性只与角锥棱镜的直角加工精度相关,而与角锥放置的位置无关.假设角锥的三个直角加工误差分别为ε1,ε2和ε3,则入射光线与反射光线之间的偏转角度为［25］

式中nk为角锥反射体的折射率,材料为普通K9玻璃,折射率为1.5168.现有加工工艺可以保证角锥棱镜的反射角误差小于2′′,从而造成的反射光线角度偏转误差小于9.9′′,再由(2)—(7)式可以计算出由双折射横向剪切分束器剪切开的两束线偏振光之间的夹角小于2.6′′,此角度误差远小于探测器单个像素对应的视场角(以像素尺寸为5.86µm,成像物镜焦距为75 mm为例),光束经过双折射横向剪切分束器后仍能够汇聚在同一个像素上.因此,角锥加工误差对反射光线的影响很小,可以实现光束的高精度横向剪切.利用角锥这一反射特性,使得分束器产生的剪切光束具有很高的平行度,提高了系统的成像质量以及干涉条纹的调制度,减少了由于Wollaston棱镜加工平行度误差以及横向剪切分束器的装调误差对复原光谱造成的影响.

图3 (网刊彩色)角锥棱镜等效展开图Fig.3.(color online)Tunnel diagram of the retroreflector.

3.3 双折射横向剪切干涉仪光程差计算

系统的横向剪切分束器主要由Wollaston棱镜和角锥反射体组成,它是分裂光束并产生光程差的核心元件.剪切光束产生的光程差是对探测目标进行干涉调制的关键,是复原光谱信息前提,因此推导光程差的精确计算公式,对高光谱成像系统的研究与设计具有重要意义.

根据折射定律,eo光和oe光在角锥内与x轴的夹角ϕeo和ϕoe分别为

采用光线追迹的方法分析eo光的传播光程,光线在双折射横向剪切分束器内的传播路径如图4所示,设光线在第一块Wollaston棱镜入射点A的坐标为(0,yA),分析光线与Wollaston棱镜各光学面所在直线的方程表达式,可得出以下关系:

其中B1(xB1,yB1)为光线与第一块Wollaston棱镜胶合面的交点坐标;C1(xC1,yC1)为光线在第一块Wollaston棱镜出射点的坐标;D1(xD1,yD1)为光线在角锥等效展开平板入射点的坐标:E1(xE1,yE1)为光线在角锥等效展开平板出射点的坐标;F1(xF1,yF1)为光线在第二块Wollaston棱镜入射点的坐标;G1(xG1,yG1)为光线与第二块Wollaston棱镜胶合面的交点坐标;H1(xH1,yH1)为光线在第二块Wollaston棱镜出射点的坐标.同理,可以计算出oe光线与Wollaston棱镜各光学面的交点坐标,则两束光线的光程差为

图4 (网刊彩色)双折射横向剪切分束器光路图Fig.4.(color online)Schematic of the optical path in the birefringent lateral shearing splitter.

3.4 调制度分析

干涉型高光谱成像系统中,光束在Wollaston棱镜内分裂为o光与e光,两束光的光强比主要与半波片快轴的方位角以及相位延迟量δ(σ)相关.假设半波片快轴方位角与y轴(偏振分光棱镜透振方向)的夹角为ζ,入射光的复振幅E,当入射光为单色光时,经过偏振分光棱镜反射的两束干涉光强为

当cos(2πσL)=−1时,可以得到干涉光强的最小值为零.因此,双折射横向剪切分束器产生的干涉条纹调制度为K=(Imax−Imin)/(Imax+Imin)=1,并且干涉条纹调制度与Wollaston棱镜内两束正交偏振光的光强比无关.另外,由(12)式还可以看出,半波片快轴的方位角以及相位延迟量δ(σ)直接影响干涉光强的辐值.若半波片采用消色差半波片,它的快轴方位角取22.5°时,各波段处采集到的光强幅值最大.若采用未消色差的半波片,则需要对采集到的光强幅值进行校正,利用椭偏仪测量出各波段的相位延迟量,再由(12)式可求得该校正系数.

4 实验与分析

4.1 实验装置

按照上述原理分析,搭建了实验装置进行实验测试.系统中三个成像物镜的焦距为75 mm,F数为1.8,半波片快轴方位角与y轴的夹角为22.5°.剪切干涉系统的Wollaston棱镜采用方解石(冰洲石)材料,它的Sellmeier方程式为

其双折射特性与入射光波长的关系曲线如图5所示.Wollaston棱镜结构角为α=3°,厚度t=5 mm,通光口径为14 mm×14 mm.角锥棱镜的材料为K9冕牌玻璃,折射率nk=1.5168,厚度为b=9.5 mm,通光口径为12.7 mm.Wollaston棱镜出射面与角锥棱镜入射面之间的空气隙距离为d=15 mm.探测器型号为POINT GREY GS3-U3-23S6 M-C,像素数量为1920 pixel×1200 pixel,像素尺寸为5.86µm.

图5 (网刊彩色)方解石晶体折射率随波长变化曲线Fig.5.(color online)The variation curves of refractive index with wavelength in calcite crystal.

4.2 光程差与视场角调制关系

光谱系统在窗扫模式下进行成像探测时,是基于视场角与光程差的关联调制.利用(11)式进行分析仿真,角锥顶点偏移量为h=0 mm,可以得到光程差与视场角的关系曲线.图6(a)给出了波段范围为400—1000 nm时光程差随视场角的变化曲线,图6(b)分别给出了400,700和1000 nm处的光程差曲线.从仿真结果可以看出,光程差与视场角存在非线性调制关系,并且由于双折射剪切分束器的色散特性,使得不同波长处的光程差存在差异.

进一步分析窗扫模式下剪切分束器的光程差色散非线性特性.假设以波长在633 nm处的光程差曲线I(λ0,θ)为基准,分析波长λ处光程差随视场角θ的变化曲线I(λ,θ),定义波长λ处的光程差挤压比例系数为

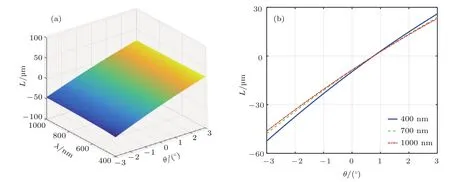
图6 (网刊彩色)光程差随视场角和波长的变化曲线Fig.6.(color online)Optical path di ff erence(OPD)distribution of incident angle θ and wavelength λ.

图7 (网刊彩色)(a)光程挤压比例系数;(b)光程差误差Fig.7.(color online)(a)Squeezing coefficient of the OPD;(b)remainder error of the OPD.

式中N为采样点个数.图7(a)给出了波长400—1000 nm范围内的光程挤压比例系数,原始光程差与按照比例系数r(λ)挤压后光程差相比,光程差误差∆L(λ,θ)为

图7(b)为误差分布情况,可以看出,光程差误差在分析波段范围内均小于100 nm,满足准零光程差条件［26］,对光谱复原精度造成的影响很小.因此,可以认为各波段的光程差具有相同的非线性程度,彼此之间只是相差一个辐值挤压比例系数.光程差的这种特性有利于使用非均匀傅里叶变换方法对干涉数据进行复原处理.

4.3 光程差与角锥顶点偏移量调制关系

光谱系统在凝视成像探测时,采用内部扫描角锥的方式改变探测目标点的调制光程差.利用(11)式进行分析仿真,分析入射光线视场角为θ=0°时,可以得到光程差与角锥顶点偏移量的关系曲线.图8(a)给出了波段范围为400—1000 nm时光程差随角锥偏移量的变化曲线,图8(b)分别给出了400,700和1000 nm处的光程差曲线.分析仿真结果可知,光程差与角锥偏移量成线性调制关系,但是由于双折射剪切分束器的色散特性,使得不同波长处的光程差同样存在差异.

按照(14)式的原理分析凝视成像探测时双折射剪切分束器的光程差色散特性.以633 nm处的光程差为基准,波长400—1000 nm范围内的光程挤压比例系数如图9(a)所示.分析图9(b)中光程差误差分布情况,光程差误差在分析波段范围内均小于100 nm,同样满足准零光程差条件,对光谱复原精度造成的影响较小.

图8 (网刊彩色)光程差随角锥偏移量和波长的变化曲线Fig.8.(color online)OPD distribution of displacement h and wavelength λ.

图9 (网刊彩色)(a)光程挤压比例系数;(b)光程差误差Fig.9.(color online)(a)Squeezing coefficient of the OPD;(b)remainder error of the OPD.

4.4 实验验证

根据系统干涉调制的原理,搭建了基于双折射剪切分束器的高光谱成像系统.利用波长为650 nm的激光作为光源进行光程差验证实验.首先,探测器采集一幅干涉图,提取一行干涉光强信息进行相位提取,得到干涉光程差与视场角的关系曲线,如图10(a)所示.实验光程差与理论光程差存在的误差如图10(b)所示,光程差误差在0.015µm范围内,误差对光谱信息复原精度影响较小.由于探测过程中无运动扫描部件,所以光程差误差主要由探测器本身噪声引起.

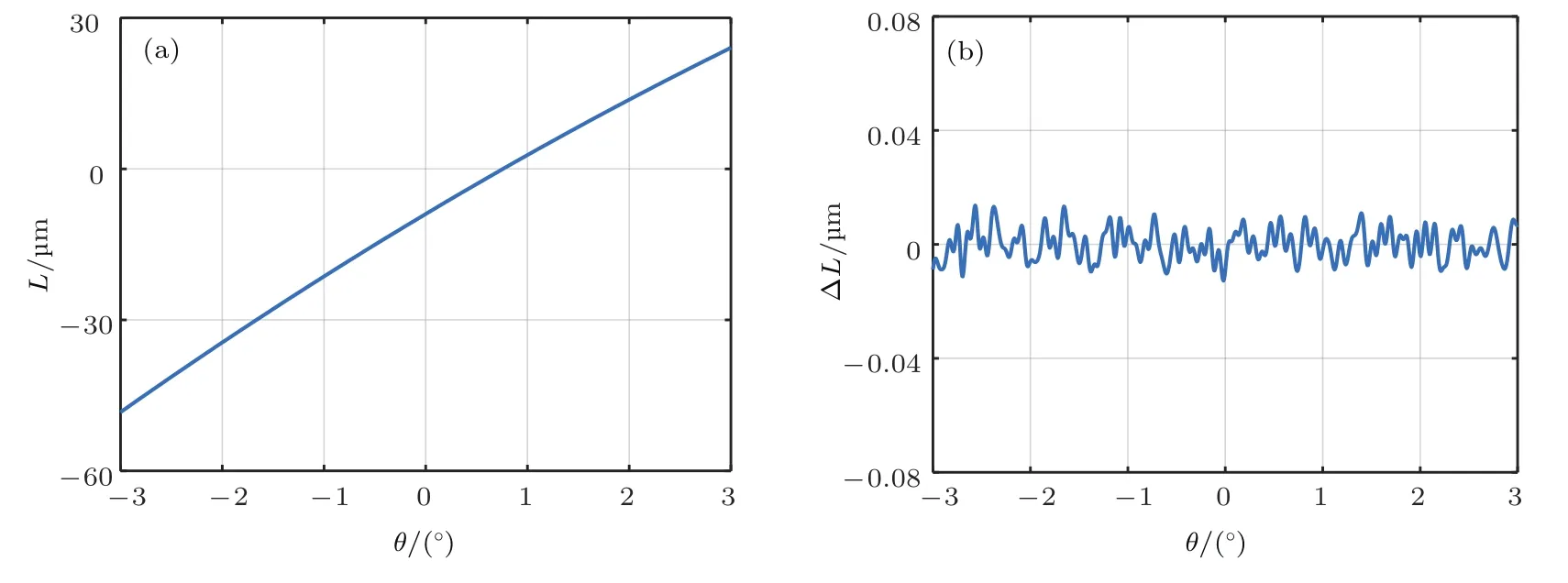
图10 (a)光程差与视场角变化曲线;(b)光程差误差Fig.10.(a)The curve of OPD at λ =650 nm with incident angle θ；(b)error of the OPD between experimental and theoretical analysis.

图11 (a)光程差与角锥偏移量变化曲线;(b)光程差误差Fig.11.(a)The curve of OPD at λ=650 nm with incident displacement h;(b)error of the OPD between experimental and theoretical analysis.

在此基础上,利用高精度电动旋转装置对角锥棱镜进行推扫,探测器视场中心像素点采集到一系列光强信息,利用相同的相位提取方法对干涉光强信息进行处理,得到干涉光程差与角锥偏移量的关系曲线,如图11(a)所示.实验光程差与理论光程差之间的误差如图11(b)所示,光程差误差在0.04µm范围内,同样满足准零光程差条件,对光谱信息复原精度影响较小.由于凝视成像模式的探测过程中存在运动扫描部件,所以光程差误差稍大于窗扫模式下的光程差误差.

图12 (网刊彩色)(a)—(c)目标场景干涉条纹;(d)矩形区域干涉条纹的放大图像Fig.12.(color online)(a)–(c)Scene interferograms;(d)enlarged interferogram of the rectangular region.

图13 (网刊彩色)不同波段处的光谱图像Fig.13.(color online)Spectral images at di ff erent wavelengths.

采用搭建的实验装置对白炽灯照射的目标场景进行成像实验,采用凝视成像探测模式,图12(a)—(c)为探测器采集到的三幅干涉图像,将图12(c)中干涉条纹所在区域放大后如图12(d)所示.可以看出,实验得到的干涉图像纹理清晰,表明基于新型双折射横向剪切分束器的高光谱成像系统能够获取清晰、对比度较好的干涉图像.按照采集序列依次提取图像中各个点的干涉光强信号并进行光谱数据反演,图13给出了四个波段处的复原光谱图像,光谱图像细节成像清晰,初步验证了本方法的可行性.

5 结 论

本文提出的新方案与基于双Wollaston棱镜和Savart偏光镜的双折射干涉型高光谱成像技术方案相比,具有以下的特点.首先,系统的复杂度低.为了保证较好的光束剪切特性,基于双Wollaston棱镜的横向剪切分束器需要保证两片Wollaston棱镜的加工结果一致性;而基于Savart偏光镜的横向剪切分束器,由于Savart单板光轴的方向与入射面不平行,在相同加工精度情况下,Savart单板的加工难度高于Wollaston棱镜.此外,基于双Wollaston棱镜或Savart偏光镜的横向剪切分束器在装调时,两片Wollaston棱镜(或两片Savart单板)的光轴方向需要严格满足设计要求,系统的装调难度大.本文提出横向剪切分束器由单个Wollaston棱镜和角锥反射体组合而成,由于角锥反射体具有严格的后向反射特性,因此任意一条进入通光孔径的入射光线,都将按原方向从入射面反向出射.入射光束在横向剪切分束器中两次经过同一片Wollaston棱镜,即使Wollaston棱镜存在加工误差和装调误差,光束仍能够被严格地横向剪切为两束平行光并发生干涉,保证了干涉条纹的调制度.因此,本文所提方法具有更低的复杂度,可以降低加工和装调难度.其次,系统的稳定性好.在新型横向剪切分束器中,剪切光束的平行性不再依赖于Wollaston棱镜和角锥反射体的放置方位,只与角锥棱镜的直角加工精度相关.在现有加工工艺水平的基础上,角锥加工误差对剪切光线平行性造成的影响远小于其他双折射横向剪切分束器加工误差和装调误差的影响,因此能够实现光束的高精度横向剪切.最后,系统的光路设置为同时实现高分辨率成像提供了一种有效的技术途径.入射光束经过PBS后,一部分光束进入WP,另外一部分被反射出去.而反射的这部分光束,正好可以被更高采样分辨率的探测器接收成像.和其他双折射干涉仪相比,双探测器形式在保持相同光通量性能的同时增强了目标的细节探测能力,可应用于微观光谱成像和其他高分辨成像领域.

为探索新的干涉高光谱成像技术方案,本文提出了一种基于双折射剪切分束器的高光谱成像新方法,利用双折射晶体分光特性以及角锥反射体的平行反射特性,实现一种结构稳定、低复杂度的高光谱成像系统.在分析横向剪切分束器中光的传播特性的基础上,详细推导了系统干涉光程差与入射光视场角以及角锥顶点偏移量之间的物理关系,并对其进行仿真分析.基于理论分析结果搭建了实验装置,利用激光光源对光程差进行分析验证,实验结果与理论分析结果匹配较好,从而验证了系统光束剪切特性分析结果的准确性,为精确光谱复原提供理论依据,对双折射偏振干涉高光谱成像系统的研究、设计和应用具有重要意义.

［1］Posselt W,Holota K,Tittel H O,Harnisch B 2001Proceedings of the Fourier Transform SpectroscopyCoeur d’Alene,Idaho,United States,February 5,2001 FMD10

［2］Ferrec Y,Taboury J,Sauer H,Chavel P,Fournet P,Coudrain C,Deschamps J,Primot J 2011Appl.Opt.50 5894

［3］Wang W C,Liang J Q,Liang Z Z,Lü J G,Qin Y X,Tian C,Wang W B 2014Opt.Lett.39 4911

［4］Rafert J B,Sellar R G,Holbert E,Blatt J,Tyler D W,Durham S,Newby H 1994Proc.SPIE2198 338

［5］Barducci A,Guzzi D,Lastri C,Marcoionni P,Nardino V,Pippi I 2010Opt.Express18 11622

［6］Cabib D,Lavi M,Gil A,Milman U 2011Proc.SPIE8012 80123H

［7］Crites S T,Lucey P G,Wright R,Garbeil H,Horton K A,Wood M 2012Proc.SPIE8385 838509

［8］Li J X,Bai C X,Shen Y,Xu D L 2016Opt.Lett.41 5329

［9］Xiang L B,Yuan Y,Lü Q B 2009Acta Phys.Sin.58 5399(in Chinese)［相里斌,袁艳,吕群波 2009物理学报58 5399］

［10］Horton R F 1996Proc.SPIE2819 300

［11］Pisani M,Zucco M 2009Opt.Express17 8319

［12］Bai C X,Li J X,Meng X,Shen Y,Zhu R H 2015Acta Opt.Sin.35 0811002(in Chinese)［柏财勋,李建欣,孟鑫,沈燕,朱日宏2015光学学报35 0811002］

［13］Smith W H,Hammer P D 1996Appl.Opt.35 2902

［14］Zhang C M,Xiangli B,Zhao B C,Yuan X J 2002Opt.Commun.203 21

［15］Harvey A R,Fletcher-Holmes D W 2004Opt.Express12 5368

［16］Craven J,Kudenov M W,Stapelbroek M G,Dereniak E L 2011Appl.Opt.50 1170

［17］Mu T K,Zhang C M,Ren W Y,Jia C L 2012Opt.Lett.37 3507

［18］Fossi A P,Ferrec Y,Roux N,D’almeida O,Guerineau N,Sauer H 2016Opt.Lett.41 1901

［19］Li J,Zhu J P,Zhang Y Y,Liu H,Hou X 2013Acta Phys.Sin.62 024205(in Chinese)［李杰,朱京平,张云尧,刘宏,侯洵2013物理学报62 024205］

［20］Quan N C,Zhang C M,Mu T K 2016Acta Phys.Sin.65 080703(in Chinese)［权乃承,张淳民,穆廷魁 2016物理学报65 080703］

［21］Zhang C M,Mu T K,Ren W Y,Zhang L,Liu N 2010Opt.Eng.49 043002

［22］Li Q W,Zhang C M,Wei Y T,Chen Q Y 2015Acta Phys.Sin.64 224206(in Chinese)［李祺伟,张淳民,魏宇童,陈清颖2015物理学报64 224206］

［23］Bai C X,Li J X,Shen Y,Zhou J Q 2016Opt.Lett.41 3647

［24］Yu D Y,Tan H Y 2015Engineering Optics(Beijing:China Machine Press)p48(in Chinese)［郁道银,谈恒英2015工程光学(北京:机械工业出版社)第48页］

［25］Lin L B 2007M.S.Dissertation(Wuhan:Huazhong University of Science and Technology)(in Chinese)［林来宾2007硕士学位论文(武汉:华中科技大学)］

［26］Wu H Y,Zhang C M,Zhao B C 2009Acta Phys.Sin.58 930(in Chinese)［吴海英,张淳民,赵葆常2009物理学报58 930］

Beam shearing characteristic analysis of interferometric hyperspectral imaging system∗

Li Jian-Xin1)2)†Bai Cai-Xun1)2)Liu Qin1)Shen Yan1)Xu Wen-Hui1)Xu Yi-Xuan1)
1)(School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
2)(MIIT Key Laboratory of Advanced Solid Laser,Nanjing University of Science and Technology,Nanjing 210094,China)

A birefringent Fourier transform imaging spectrometer with a new lateral shearing interferometer is presented.The interferometer includes a Wollaston prism and a retrore fl ector.It splits an incident light beam into two shearing parallel parts to obtain interference fringe patterns of an imaging target,which is well established as an aid in reducing problems associated with optical alignment and manufacturing precision.The proposed method provides a direct technology for robust and inexpensive spectrometers to measure spectral signatures.Formulas for the optical path di ff erence(OPD)produced by the proposed birefringent interferometer are derived by the ray-tracing method.Two experiments are carried out to demonstrate the accuracy of the formulas for OPD in the inner scanning mode and window scanning mode,respectively.A laser of wavelength 650 nm is used as a source of the experimental setup.The experimental estimations of the OPD and a reference OPD curve obtained with theoretical analysis are used for comparison.The match between the two curves is highly consistent,for the maximum deviation of the experimental OPD is less thanλ/4.For the further veri fi cation of the imaging performance of the proposed method,another experiment is performed.A scene illuminated by an incandescent lamp is used as an imaging target.The temporal rotating of the retrore fl ector produces a series of time sequential interferograms,where the target is fi xed and fringe patterns move.Performing nonuniform fast Fourier transform of the interferogram data produces a spectral data cube(i.e.,the spectral images of the target).A series of recovered spectral images whose center wavelengths range from 450 to 650 nm is presented.

In this paper,the principle of the instrument is described,and the OPD distribution formula is obtained and analyzed.The performance of the system is demonstrated through a numerical simulation and three experiments.This work will provide an important theoretical basis and the practical instruction for designing a new type of birefringent Fourier transform spectrometer based on Wollaston prism and its engineering applications.

spectroscopy,interference,birefringence,optical path di ff erence

24 April 2017;revised manuscript

26 June 2017)

(2017年4月24日收到;2017年6月26日收到修改稿)

10.7498/aps.66.190704

∗国家自然科学基金(批准号:61475072)、国家重大科学仪器设备开发专项(批准号:2013YQ150829)、中央高校基本科研业务费专项

资金(批准号:30916014112-010)和江苏省研究生科研创新计划(批准号:KYLX16_0426)资助的课题.

†通信作者.E-mail:ljx@vip.163.com

©2017中国物理学会Chinese Physical Society

PACS:07.60.Rd,42.25.Hz,42.25.Lc

10.7498/aps.66.190704

*Project supported by the National Natural Science Foundation of China(Grant No.61475072),the National Key Scienti fi c Instrument and Equipment Development Projects of China(Grant No.2013YQ150829),the Fundamental Research Funds for the Central Universities,China(Grant No.30916014112-010),and the Graduate Student Innovation Project of Jiangsu Province,China(Grant No.KYLX16_0426).

†Corresponding author.E-mail:ljx@vip.163.com