自驱动颗粒体系中的熵力∗

华昀峰 章林溪

(浙江大学物理系,杭州 310027)

自驱动颗粒体系中的熵力∗

华昀峰 章林溪†

(浙江大学物理系,杭州 310027)

在许多纳米复合材料体系中熵力(entropy force)是普遍存在的,但由于熵力的存在会导致纳米颗粒的凝聚从而降低其许多性能,因此在大多数情况下熵力的存在对体系并无益处,所以研究如何减小熵力对体系的影响是非常重要的.不带角速度的自驱动粒子在熵力作用下会集聚在纳米颗粒(或者纳米棒)周围,这会对纳米颗粒(或者纳米棒)产生很大的相互作用力.对于纳米颗粒,在不带角速度的自驱动粒子体系中存在着非常大的排斥力.而对于纳米棒,由于纳米棒内外的不对称性,使得两个纳米棒之间会产生吸引-排斥转变,同时这个吸引-排斥转变与纳米棒之间的距离有关.当自驱动粒子加上一个自转角速度ω之后,熵力的作用就大大减弱,纳米颗粒不再集聚.研究结果有助于对非平衡态下纳米颗粒(或纳米棒)之间熵相互作用力的认识.

熵力,自驱动颗粒体系,非平衡态,过阻尼郎之万方程

1 引 言

熵力(entropy force)是指一个体系中的一种宏观作用力,其性质主要不是由体系中某种特定的微观作用力决定,而是表现为整个体系对于熵增加的统计趋势［1,2］.在许多纳米复合材料体系中普遍存在熵力,但由于熵力的存在会导致纳米颗粒的凝聚,从而降低其许多性能,因此在大多数情况下熵力的存在对体系并无益处,因此深入研究如何减小体系中的熵力具有重要的科学意义［3］.

在过去几十年里,自驱动粒子体系引起了人们越来越大的兴趣.自驱动粒子体系的研究对于了解自然界中像鸟群、细菌、组织以及细胞骨架等有趣的自组织现象［4］、对医学以及生物体系中的自驱动行为的认识很有帮助［5−8］.自驱动粒子的运动与布朗运动是不同的:颗粒的布朗运动是由溶剂的随机热波动引起的,而自驱动粒子是带有随机自推进的运动(但是长时间来看自驱动颗粒的运动仍为布朗运动,其运动的均方位移与时间成正比［9］),这使得自驱动颗粒产生了很多引人注目的新现象.比如细菌的输运现象［10−16］、微尺度的湍流现象［17］以及自驱动颗粒的自组装现象等［18−21］.

Ran等［19］研究了两块固定不动的板在自驱动颗粒体系中的相互作用情况,结果显示:自驱动颗粒会集聚在两板的周围,这使得两板之间产生了不同的相互作用力,同时当两板之间的距离改变时,相互作用力会有排斥-吸引交替变化的现象,这些都是熵力作用导致的.对于另外一类自驱动粒子,不仅自身具有自驱动力,而且还会自转动,具有自转动角速度,这一类称为手性(chiral)自驱动粒子.近期关于手性自驱动粒子的研究很多［22−26］,实验工作也很多［26］:Nourhani等［22］研究了自驱动粒子在一个平稳的过阻尼周期势中各种各样的漂移行为;Friedrich和Julicher［23］的研究表明手性自驱动粒子存在噪声的三维空间中也能沿螺旋路径运动;Volpe等［24］研究了如何在复杂的环境中模拟活跃的自驱动粒子的运动;Kummel等［25］实验研究了手性自驱动粒子在基底表面以及通道边界上的旋转运动,他们发现粒子的运动整体上来看和布朗运动是完全符合的.本文主要研究自驱动粒子自带自转角速度体系中熵相互作用情况,目的在于研究自驱动颗粒的自转角速度对熵力的影响.

2 模 型

本文研究自驱动粒子和两个固定不动的纳米颗粒共混以及和两块固定不动的纳米棒共混的二维体系,如图1所示.

图1 (网刊彩色)纳米颗粒(a)/纳米棒(b)与自驱动粒子组成的体系Fig.1. (color online) Complex systems of nanoparticles/self-propelled active particles(a)and nanorods/self-propelled active particles(b).

在这个体系中,自驱动粒子的直径为σ,而纳米颗粒的直径为σC=10σ.纳米棒的直径为σ,长度L=10σ.纳米颗粒之间的距离以及棒之间的距离都用d表示.每个自驱动粒子的运动都遵循过阻尼郎之万方程［11,27］,

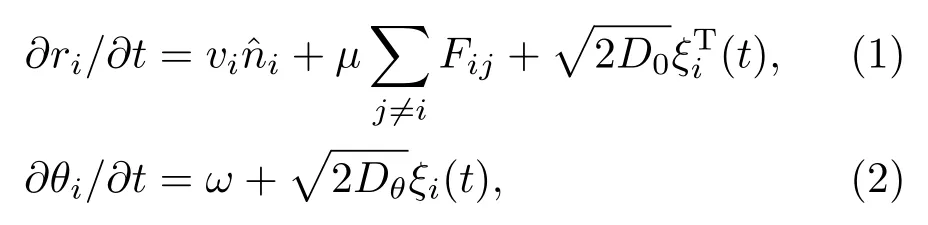
ri≡(xi,yi)表示第i个粒子质心的位置,vi和分别表示颗粒自驱动速度的大小和方向,ω表示粒子自驱动角速度,和ξi(t)表示高斯白噪声函数,满足而D0和Dθ分别表示平动和转动的扩散系数.另外,µ为阻尼系数,大小为µ=1/γ(γ为摩擦系数),是颗粒受到其他所有颗粒的合力,颗粒之间是通过Lennard-Jones(LJ)势相互作用的［11］:

这里,r表示两个颗粒之间的距离,自驱动粒子之间∆=0,而自驱动粒子与纳米颗粒之间∆=(σ+σC)/2−σ=4.5σ,LJ势作强度系数ε=5kBT,另外,我们取rc=21/6σ+∆,所以颗粒之间都是纯排斥的.

模拟过程中,纳米颗粒以及纳米棒是保持不动的,在x和y方向上都满足周期性边界条件,所有自驱动颗粒的质量相等,记为m.取kBT=1,σ=1,m=1,和τ0=(mσ2/kBT)1/2=1,分别为能量单位、单位长度σ、单位质量m和单位时间,均约化为1.体系中自驱动颗粒的密度为ϕ,自驱动粒子的自驱动速度为vi=v0=0.4(如不做其他说明),时间步长为τ=10−4τ0,且对每个体系运算1.0×108步长以确保获得稳定体系.

3 结果与讨论

图2给出了d=10,ϕ=0.1,不同ω(以v0为单位)的情况下,体系达到稳定时纳米颗粒周围自驱动颗粒的分布情况,这里ϕ=0.1对应的自驱动粒子数为234.图3给出了纳米颗粒周围自驱动粒子的径向分布函数g(r).可以清楚地看到,当ω=0时,自驱动粒子会集聚在两个纳米颗粒周围,与之相对应的,当r≈5.5时,g(r)的达到了一个峰值55,见图3,另外由于自驱动粒子的直径为1,因此在r≈6.5,7.5也出现了峰值.在纳米颗粒之间的区域(如图2所示),集聚了大量的自驱动粒子,这会产生很大的熵力,使得两个粒子之间产生很大的排斥力［19,21］.而当ω=10v0时,自驱动粒子几乎是均匀分布的,相应的g(r)没有出现峰值,此时纳米颗粒之间不存在排斥力.由图3可知,自驱动粒子的角速度越大,粒子分布的越均匀.所以,给自驱动粒子增加一个角速度可以减小熵力对体系的影响.

图2 (网刊彩色)纳米颗粒周围的自驱动颗粒分布情况(d=10,ϕ=0.1)Fig.2. (color online)Snapshots of active particles around nanoparticles with d=10 and ϕ=0.1.

图3 (网刊彩色)纳米颗粒周围自驱动颗粒的径向分布函数g(r)(d=10,ϕ=0.1)Fig.3.(color online)Radial distribution functions g(r)of active particles around nanoparticles with d=10 and ϕ=0.1.

为了证明这一结论,计算了在不同角速度ω时,x方向上大粒子之间的受力情况,结果如图4所示,F表示纳米颗粒受到的熵力,通过计算周围粒子对纳米颗粒总的作用力而得到［19,26］.图4中的三条线分别代表的是d=10,12,和15三种情形.当角速度ω很小时,大粒子之间存在着吸引-排斥相互作用力的转变.当ω=0时,d=12时的排斥力要比d=10的大,这是因为d=12时,两个大粒子之间聚集了更多的颗粒产生了更大的熵力.而当d=15时,两个纳米颗粒之间存在较小的吸引力.同时随着角速度ω的不断增大,纳米颗粒之间的相互作用力会不断减小直至为零.

图4 不同角速度ω时两个纳米颗粒之间的相互作用力Fig.4.Forces between two nanoparticles with di ff erent angular velocities ω.

由图4可知,体系中的两个纳米颗粒之间的作用力不仅与角速度的大小有关系,还与纳米颗粒之间的距离有关.图5给出了在不同的v0情况下(角速度ω=0),纳米颗粒之间的作用力与纳米颗粒之间距离d的关系.根据图3可知,在纳米粒子周围的自驱动粒子的径向分布函数的第一个峰值出现在5.5的位置上,且第一个峰值远比第二、第三个峰值大,所以当d=11时,两个纳米粒子之间会集聚很多的粒子,从而产生很大的熵力,此时的排斥力最大.随着距离的增大,纳米颗粒之间的作用力会越来越小.因此增加自驱动颗粒的自驱动速度v0可以增大两个纳米颗粒之间的排斥相互作用力.

图5 不同自驱动速度下不同距离d时两个纳米颗粒之间的作用力Fig.5.Forces between two nanoparticles with di ff erent self-propelled velocities v0.

图6分别给出了ϕ=0.4,(a)角速度ω=0不变,改变两个纳米棒之间的距离时自驱动颗粒的分布情况和(b)两棒间距d=2.5不变,改变ω时自驱动粒子的分布图.ϕ=0.4体系对应的自驱动粒子数为392.由图6(a)可以看出,ω=0的自驱动粒子会在熵力的作用下,集聚在纳米棒的周围,而随着两棒之间的距离d的变化,自驱动粒子的集聚情况会有所不同,这就对棒产生不同的作用力［19］.当ω̸=0时,自驱动粒子就会做不规则的、半径近似为r0≈ω/v0的圆周运动.当角速度ω不断增大时,自驱动粒子的运动半径会越来越小,从而不会产生集聚的现象(如图6(b)所示).

图7和图8分别给出了与图6(a)和图6(b)对应的两个纳米棒受力情况.由图7可以看出,两棒间的作用力F会随着两棒间距离的变化而交替变化,该结果与Ran等［19］的结果类似.而由图8可知,随着ω的不断增大,两棒间的作用力不断减小.该结果与纳米颗粒情况类似,这充分说明了角速度的加入可以减小熵力对体系的影响.

图6 (网刊彩色)(a)角速度ω=0不变,两棒距离d不同时自驱动颗粒的分布图;(b)两棒间距d=2.5不变,改变角速度ω时自驱动颗粒的分布图Fig.6.(color online)(a)Snapshots of active particles with di ff erent distances d of two nanorods at ω=0,and(b)snapshots of active particles with di ff erent angular velocities ω at d=2.5.

图7 角速度ω=0时两棒之间的作用力与两棒距离d的关系Fig.7.Forces between two parallel nanorods as a function of distance d with ω=0.

图8 两棒之间的作用力与角速度ω的关系Fig.8.Forces between two nanorods as a function of ω with d=2.5 and 3.0.

4 总 结

不带角速度的自驱动颗粒在熵力作用下会集聚在纳米颗粒(或者纳米棒)周围,这会对其产生很大的相互作用力,而由于两纳米颗粒(或者纳米棒)内外的不对称性,使得纳米颗粒(或者纳米棒)之间产生的吸引-排斥相互作用的转变,这个转变与纳米颗粒(或者纳米棒)之间的距离有关.当自驱动颗粒加上一个角速度ω之后,熵力的作用就会较弱,颗粒就不再集聚,这种相互作用随着自驱动粒子角速度ω增加而减弱.这些研究能够帮助我们加深对非平衡状态下纳米颗粒的分散-集聚转变的认识.

［1］Asakura S,Oosawa F 1958J.Polym.Sci.33 183

［2］Joanny J F,Leibler L,de Gennes P G 1979J.Polym.Sci.Part B:Polym.Phys.17 1073

［3］Jiang Y W,Zhang D,He L L,Zhang L X 2016J.Phys.Chem.B120 572

［4］David G R,Guevorkian K,Douezan S 2012Science338 910

［5］Fily Y S,Henkes S,Marchetti M C 2014Soft Matter10 2132

［6］Zhao B,Qi N,Zhang D S 2017Mat.Rev.31 1A

［7］Ford R M,Harvet R W 2007Adv.Mater.Res.30 1608

［8］Yang W,Misko V R,Nelissen K,Kong M,Peeters M 2012Soft Matter8 5175

［9］Hagen B T,Tee ff elen S V,Löwen H 2011J.Phys.Condens.Matter23 194119

［10］Leonardo R D,Angelani L,DellArciprete D,Ruocco G,Iebba V,Schippa S,Conte M,Mecarini F,Angelis F D,Fabrizio E D 2010Proc.Natl.Acad.Sci.USA107 9541

［11］Ai B Q 2016Sci.Rep.6 18740

［12］Kaiser A,Peshkov A,Sokolov A 2014Phys.Rev.Lett.112 158101

［13］Pototsky A,Hahn A M,Stark H 2013Phys.Rev.E87 042124

［14］Potiguar F Q,Farias G A,Ferreira W P 2014Phys.Rev.E90 012307

［15］Koumakis N,Maggi C,Leonardo R D 2014Soft Matter10 5695

［16］Ai B Q,Zhu W J,He Y F,Zhong W R 2016J.Stat.Mech.17 023501

［17］Wensink H,Dunkel J,Heidenreich S,Drescher K,Goldstein R,Löwen H,Yeomans J 2012Proc.Natl.Acad.Sci.USA109 14308

［18］Cai J H,Wei X X,Fan A 2016Polym.Bull.4 17

［19］Ran N,Martien A C S,Peter G B 2015Phys.Rev.Lett.114 018302

［20］Hooper J B,Schweizer K S 2006Macromolecules39 5133

［21］Harder J,Mallory S A,Tung C,Valerian C,Cacciuto A 2014J.Chem.Phys.141 194901

［22］Nourhani A,Crespi V H,Lammert P E 2015Phys.Rev.Lett.115 118101

［23］Friedrich B M,Julicher F 2009Phys.Rev.Lett.103 068102

［24］Volpe G,Gigan S,Volpe G 2014Am.J.Phys.82 659

［25］Kummel F,ten Hagen B,Wittkowski R,Buttinoni I,Volpe G,Lowen H,Bechinger C 2013Phys.Rev.Lett.110 198302

［26］Yamchi M Z,Naji A 2017 arXiv:1704.07262

［27］Hasnain J,Menzl G,Jungblut S,Dellago C 2017Soft Matter13 930

Entropy forces of nanoparticles in self-propelled systems∗

Hua Yun-Feng Zhang Lin-Xi†
(Department of Physics,Zhejiang University,Hangzhou 310027,China)

Entropy force is fairly ubiquitous in nature,but it is not practically bene fi cial for most cases,thus how to reduce the entropic force of the system is very important.In this paper,by employing the overdamped Langevin dynamics simulations,we explore the entropy force between two large nanoparticles(or two nanorods)immersed in a self-propelled system.Self-propelled particles can be regarded as active matter,and the active matter is an interesting subject which has been studied theoretically and experimentally over the past few years.A great many biological and physical systems can be referred to as active matter systems,including molecular motors,swimming bacteria,self-propelled colloids,motile cells,and macroscopic animals.Active matter obtains energy from an external system under non-equilibrium conditions,and active particles with suitably designed constructions are able to convert energy input into the desired control of function,which has wide potential applications in a diversity of fi elds,such as drug delivery in medicine.Self-propelled particles without angular velocity would gather around the nanoparticles(or nanorods)under the e ff ect of entropy force,which can induce large entropy force between nanoparticles.The interaction force between two nanoparticles is large enough,owing to the asymmetry of the system,and entropy force also depends on the distance between two nanoparticles(or two nanorods).For the case of self-propelled particles with an angular velocity,the entropic e ff ect is weak,and the larger the angular velocity,the weaker the entropic force is.Moreover,nanoparticles will no longer assemble together because of their weak entropic forces.Meanwhile,the entropy force between two nanorods can be tuned from a long repulsion into a long range attraction by changing the distance between two nanorods.The present investigation can help us understand the entropy forces in non-equilibrium systems.

entropy force,self-propelled particle system,non-equilibrium system,overdamped Langevin equations

14 February 2017;revised manuscript

13 June 2017)

(2017年2月14日收到;2017年6月13日收到修改稿)

10.7498/aps.66.190701

∗国家自然科学基金(批准号:21374102,21674096)资助的课题.

†通信作者.E-mail:lxzhang@zju.edu.cn

©2017中国物理学会Chinese Physical Society

PACS:07.05.Tp,77.84.Jd,78.40.Pg,78.67.Qa

10.7498/aps.66.190701

*Project supported by the National Natural Science Foundation of China(Grant Nos.21374102,21674096).

†Corresponding author.E-mail:lxzhang@zju.edu.cn