液体材料超声处理过程中声场和流场的分布规律研究∗

吴文华 翟薇† 胡海豹 魏炳波

1)(西北工业大学理学院,西安 710072)

2)(西北工业大学航海学院,西安 710072)

液体材料超声处理过程中声场和流场的分布规律研究∗

吴文华1)翟薇1)†胡海豹2)魏炳波1)

1)(西北工业大学理学院,西安 710072)

2)(西北工业大学航海学院,西安 710072)

针对合金熔体等液体材料的超声处理过程,选取水作为透明模型材料,采用数值模拟计算和示踪粒子实验方法,研究了20和490 kHz两种频率超声作用下水中的声场和流场分布.结果表明,增大变幅杆半径能够提高水中声压水平,扩大空化效应的发生区域.当超声频率为20 kHz时,水中声压最大值出现在超声变幅杆下端面处,且声压沿传播距离的增大而显著减小.如果超声频率增加至490 kHz,水中的声压级相比于20 kHz时明显提高,且声压沿着超声传播方向呈现出周期性振荡特征.两种频率超声作用下水中的流场呈现相似的分布特征,且平均流速均随着变幅杆半径增大表现出先升高后降低的趋势.变幅杆半径相同时,20 kHz频率超声作用下水中的平均流速高于490 kHz频率超声.采用示踪粒子图像测速技术实时观察和测定了水中的流速分布,发现其与计算结果基本一致.

超声,声场,流场,空化效应

1 引 言

在金属熔体凝固的过程中施加功率超声能调控金属的结晶过程、细化凝固组织,在材料制备领域有着广泛应用［1−8］.这是由于超声波在液体中传播时能够产生空化、声流等非线性效应,从而改善材料内部组织结构并优化其性能［9−14］.所谓空化效应,是指当水中的声压超过某一临界值时,其中振荡的气泡会发生破灭和崩塌,从而形成局部瞬时的高温高压,显著改变液相中的热力学状态.而声流是由于声压梯度的存在而在液体内部形成的整体性环流,能够大大加速与相变过程相关的传热和传质速度.由此可见,液相内部的声压分布、发生空化效应的体积以及声流形态和流速大小是衡量超声波对液相作用效果的主导因素.

从超声施振的方式而言,通常采用将超声变幅杆直接插入液相中一定深度进行施振.在这种情况下,超声频率、功率、变幅杆半径和液体种类等参数都能够改变液相中的声场和流场分布特征［15］,成为影响超声对液相作用效果的重要参数.如果只是进行实验研究,限于实验装置和条件,研究者通常只能改变单一或少数参量,而无法全面考察各种实验参量对声场和流场分布的作用规律.因此,建立超声波在液相中传播的声场和流场理论模型,研究各种参数对超声作用效果的影响,就成为亟待解决的科学问题.目前,国际上已经有一些相关的研究报道.如Trujillo和Kai［16］研究了超声频率为20 kHz时水中的流速分布;Kojima等［17］测量了490 kHz超声作用下水中的声压和流速分布.然而,不同超声频率和变幅杆半径作用下的声场和流场变化特征尚不明确.通过构建理论模型,能够总结出这些参量对声场和流场分布的作用规律,为揭示超声波在合金凝固过程中的传播规律奠定基础.

由于水和熔融铝的相关流体性质类似,如室温下水的动力黏度和熔融铝的动力黏度是一个量级,且二者的声谱在整个宽带频谱上分布类似,可以认为水和熔融铝在超声处理下具有相似的行为［18］.另外,合金熔体中的流场无法直接观察,而水作为透明液体,可以用示踪粒子图像测速技术直接测量出超声作用下水中的流场,与构建的模型进行比较,以此来验证模型的正确性,从而可以将模型推广到合金熔体中去.因此,本文选取水为透明模型材料,建立了超声波在液态水中传播的声场和流场理论模型,数值计算了水中声压级和流速分布,研究了超声频率和变幅杆半径对声场分布、空化体积、流场形态和流速的改变规律.同时,采用粒子图像测速技术实时观察了水中的流线分布,并通过对流速的精确测定,验证了计算结果的正确性.

图1 数值分析模型示意图 (a)三维几何模型;(b)声场边界条件;(c)流场边界条件;1,变幅杆;2,水;3,玻璃容器Fig.1.Schematic of numerical model:(a)Three-dimensional geometric model;(b)two-dimensional axisymmetric sound fi eld boundary;(c)two-dimensional axisymmetric flow fi eld boundary;1,horn;2,water;3,glass container.

2 数值模拟和实验方法

2.1 声场模拟分析

三维几何模型如图1(a)所示,半径为50 mm、高为100 mm、厚度为10 mm的圆柱体玻璃容器中装满液态水.超声变幅杆从容器顶面中心插入液面以下30 mm,变幅杆半径R分别为1,20,40和49 mm.水中的谐波方程为

方程(1)中,p代表声压;角频率定义为ω=2πf,其中f为超声频率;ρc和cc分别代表水和石英的复密度和复声速,表示为

复波数kc和阻抗Zc可用下式表示:

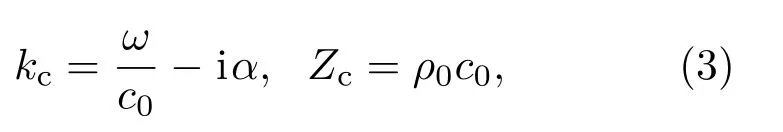
其中,α是声吸收系数,c0和ρ0分别表示水中的声速和水密度.计算过程中所用到的物理量数值如表1所列.

表1 数值模拟中用到的物理量数值Table 1.Value of parameter in numerical simulation.

由于该模型关于中心轴对称,故石英容器中的声场分布可由中心截面上的声场旋转一周生成,其几何边界条件如图1(b)所示.在水-空气和石英-空气界面上满足阻抗边界条件:

其中,Ze=ρece是外部区域的阻抗(ρe和ce分别代表空气的密度和空气中的声速),n为垂直于壁面的单位矢量.超声变幅杆的作用等效为施加在液面中心的压力,初始压强大小恒定为9.42×105Pa.在水和石英中的初始声压均设置为0 Pa,分别研究20和490 kHz频率超声作用下水中的声场分布.在计算过程中,根据有限元方法,使用三角形网格划分,将整个计算区域剖分为约10000个网格,计算的自由度数约为20000个.

2.2 流场模拟分析

流场由运动方程(方程(5))以及连续性方程(方程(6))得到:

其中,τ表示黏度的压力张量,I为单位矩阵,u和p分别是流速和液体中的压力,F表示产生声流的单位体积上的力.结合方程(5)和(6),体积力表示为［21］

µ为液体黏度,µb为体积黏性系数,p2和u2是声压和流速的二阶近似的时间独立量.在不考虑其他外力作用下,产生声流的体积力仅由声辐射力提供,此时体积力即为声场产生的声辐射力Fac,表示为［22］

其中,uac是由声波在液体中传播产生的振荡速度,使用驻波近似p≈uacρ0c0［22］,则声辐射力的大小可以表示为［23］

将通过声场模型得到的水中声压场导入到方程(9)中,计算得到声辐射力.再将声辐射力导入流场模型中,即可算出容器中的流场分布.

流场边界条件如图1(c)所示.与计算水中声压分布的模型相同,只计算石英容器中心截面上的流场分布.利用有限元计算方法,整个计算区域包括约100000个三角形网格,计算的自由度数约为260000个.

2.3 流场的实时观测

如图2所示,利用粒子图像测速技术测定了20 kHz超声作用下纯水中的流场分布.在底面半径为40 mm、高为100 mm、厚度为5 mm的烧杯里装满水,将半径为10 mm的变幅杆插入液面以下30 mm.在水中加入粒径为20—30µm、密度为1 g/cm3的硼硅酸盐空心玻璃微珠作为示踪粒子.激光光源选用功率为7 W的二极管抽运固体激光器,激光波长为532 nm.实验过程中,将激光器、烧杯和超声变幅杆的中心固定在一条直线上.当超声换能器开始作用时,打开激光光源,通过高速摄像机捕捉到2.5 s曝光时间内示踪粒子在水中的运动状态,然后将数据导入PIVlab软件中,从而测算出水中的流场分布.

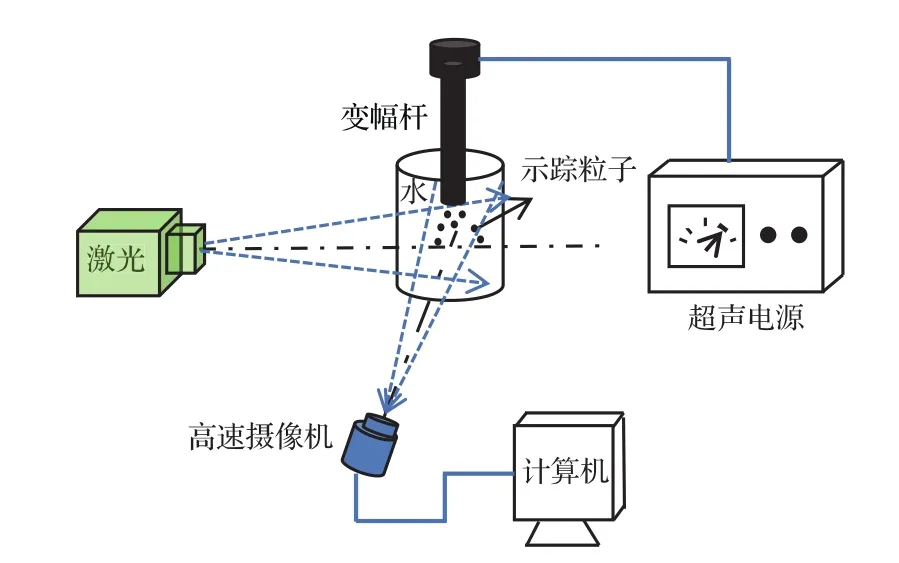
图2 示踪粒子图像测速实验示意图Fig.2.Schematic of particle image velocimetry.

3 研究结果与分析讨论

3.1 声场分布特征

图3(a)为20 kHz频率超声作用下水中声压分布随变幅杆半径的变化规律.可以看出,声压沿超声传播方向呈衰减趋势.增大变幅杆半径能有效提高水中的声压水平,但位于变幅杆下端面处的声压最大值没有发生改变,均等于初始压强9.42×105Pa.进一步研究了不同半径的变幅杆作用下水中空化区域的大小.假设液体中充满半径为r0的气泡,根据气泡内外压力平衡方程以及气体状态方程,超声作用下液体强度Pt可表示为［24］

其中,Pa为大气压,Pv为水的饱和蒸气压,σ为水的表面张力系数.设声压振幅为p0,则液体中压强的幅度为|Pa±p0|,当Pa＜p0形成负压,这时空化核在负压作用下膨胀;当|Pa−p0|≥Pt(注意:Pa−p0＜0)时形成空化,即超声空化阈值Pc为

水中气泡半径r0设为1µm,温度为25°C.将相关数据代入(11)式,通过计算可以得到空化声压阈值Pc,水中声压大于Pc的区域为空化效应发生的区域,即图3(a)—(d)中黑色虚线上方的区域.由图可知,整个空化区域近似于圆锥体,且随着变幅杆半径的增大,位于变幅杆下端面附近的空化区域体积增大.

超声频率为490 kHz时不同半径的变幅杆作用下水中声压分布如图4(a)所示.随变幅杆半径的增大,水中的声压水平增大.比较了490 kHz和20 kHz频率超声作用下水中沿z轴的声压分布,如图5(a)所示.可以看出490 kHz频率超声作用下水中声压沿超声传播方向呈周期性振荡特征,与超声频率为20 kHz时声压沿传播方向呈衰减趋势大不相同.这与超声的衰减系数有关,20和490 kHz频率超声下的衰减系数分别为25和1 m−1,衰减系数越小,超声在水中越以一种近简谐运动传播,从而改变了声压在水中的分布.490 kHz频率超声作用下水中的最大声压均大于初始压强,且声压最大值在变幅杆半径为40 mm时达到12 MPa.相应地,研究了水中的空化区域随变幅杆半径的变化规律,如图4(b)所示.图中绛红色区域表示水中的空化区域.由图可知,随着变幅杆半径的增大,水中发生空化效应的区域增大.在变幅杆正下方发生空化效应的区域呈规则条纹状分布,且空化区域体积明显大于其他区域.如当变幅杆半径为40 mm时,变幅杆正下方64.96%的空间为空化区域,而其他区域只有26.73%的空间发生空化效应.

图3 (网刊彩色)超声频率为20 kHz时水中的声场和流场分布 (a)不同半径变幅杆作用下的声压分布;(b)不同半径变幅杆作用下的流速分布Fig.3.(color online)Sound fi eld and flow fi eld distribution in water under 20 kHz ultrasound:(a)The sound fi eld distribution under the horn with di ff erent radii;(b)the flow fi eld distribution under the horn with di ff erent radii.

图4 (网刊彩色)超声频率为490 kHz时水中的声场、空化区域和流场分布 (a)不同半径变幅杆作用下的声压分布;(b)不同半径变幅杆作用下的空化区域分布;(c)不同半径变幅杆作用下的流速分布Fig.4.(color online)Sound fi eld and flow fi eld distribution in water under 490 kHz ultrasound:(a)The sound fi eld distribution under the horn with di ff erent radii;(b)the cavitation area distribution under the horn with di ff erent radii;(c)the flow fi eld distribution under the horn with di ff erent radii.

比较了20和490 kHz两种频率超声作用下声压分布和水中空化体积分数随变幅杆半径的变化规律,如图5(b)所示,由图可知,相同变幅杆半径下,490 kHz频率超声作用下水中声压水平和空化体积分数均大于20 kHz频率超声.当变幅杆半径为1 mm时,两种频率超声作用下水中均不发生空化效应.而当半径增至49 mm时,20 kHz频率超声作用下水中空化区域仅占石英容器总体积的15.7%,而490 kHz频率超声作用下水中发生空化效应的区域达到总体积的66.1%.由方程(11)可知,当假设液体中充满一定半径的微气泡时,空化阈值被确定,声压大于空化阈值的区域都将发生空化效应.比较两种频率下声压分布可知,高频超声作用下水中各个区域的声压水平高于低频超声下的声压水平,使得高频超声比低频超声作用下声压大于空化阈值的区域大,因此高频超声波的空化体积分数明显大于低频的.另外,比较图5(b)中两条曲线的斜率可知,随着变幅杆半径的增大,高频超声下的空化体积分数比低频超声下的增长得快.

3.2 流场分布规律

超声频率为20 kHz时不同变幅杆半径下水中的流场分布,如图3(b)所示.图中颜色深浅代表流速的大小,箭头代表流动的方向.由图可知,增大变幅杆半径会改变水中的流线分布.当变幅杆半径分别为1,20和49 mm时,均只在石英容器的下方出现两个对称的逆时针旋转的漩涡(即图3(b1)—(b4)中的A1和A2点处);而当变幅杆半径为40 mm时,除石英容器下方的漩涡,在靠近液面处(即图3(b3)中的B1和B2点处)还存在两个对称的逆时针旋转的漩涡.随着变幅杆半径的增大,水中的最大流速先增大后减小,在变幅杆半径为40 mm时达到最大值600 mm/s.

490 kHz频率超声作用下水中的流场分布随变幅杆半径的变化规律如图4(c)所示,流场分布与20 kHz超声频率下的流场分布相似.一股射流自变幅杆中心射出,遇到底面后向两边发散.随着变幅杆半径的增大,射流半径增大.另外,在变幅杆半径为0.04 m时,除石英容器下方(即图4(c1)—(c4)中的A1和A2点处)的漩涡外,在靠近液面处(即图4(c3)中的B1和B2点处)还存在两个对称的逆时针旋转的漩涡.而其他半径下,仅在A1和A2处存在两个漩涡.

两种频率超声作用下水中的平均流速随变幅杆半径变化的拟合曲线如图6(a)所示.相同变幅杆半径下,20 kHz超声作用下水中的平均流速均大于490 kHz超声作用下水中的平均流速.随变幅杆半径的增大,20和490 kHz超声作用下水中的平均流速均先增大后减小.20 kHz频率超声作用下水中的平均流速在R=40 mm处达到最大值243.5 mm/s.而当超声频率为490 kHz时,水中的平均流速在R=40 mm处达到最大值172.7 mm/s.研究了两种频率超声作用下水中的最大流速随变幅杆半径的变化规律,如图6(b)所示.频率为20 kHz的超声作用下,水中的最大流速随变幅杆半径的增大先增大后减小,最大流速在R=33 mm处存在一个极大值.而当超声频率增至490 kHz时,水中的最大流速随变幅杆半径的增大出现两个极大值.

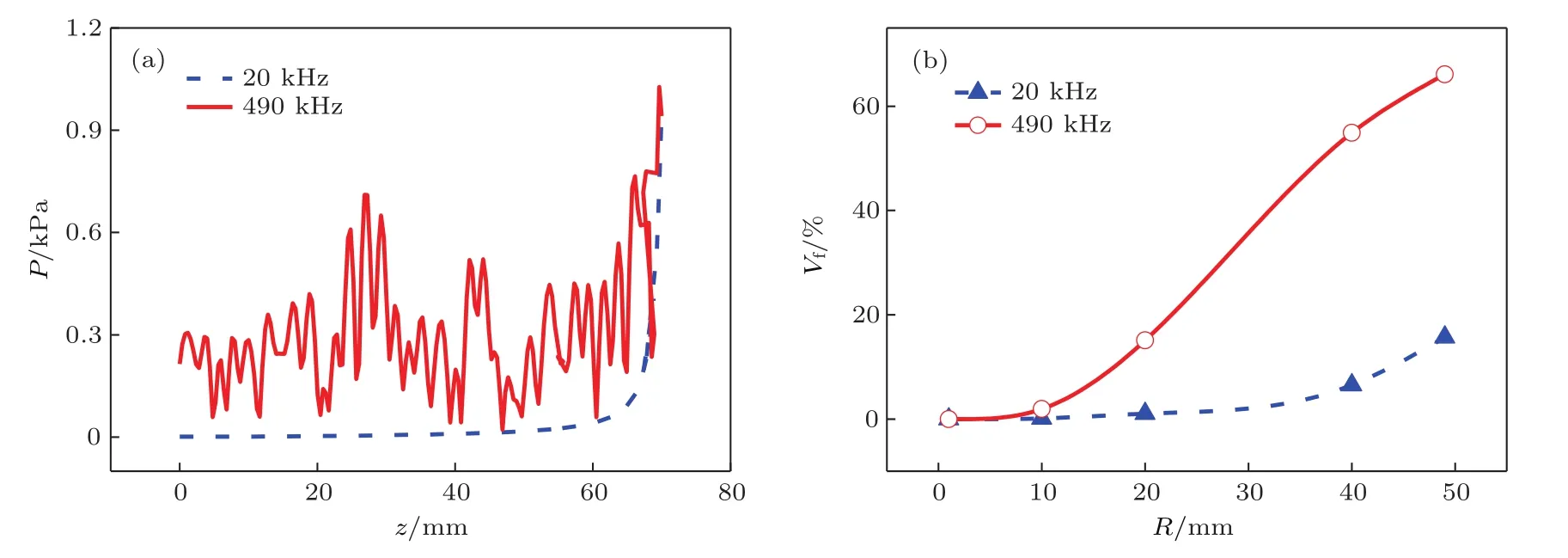
图5 (网刊彩色)不同频率超声作用下水中声场的比较 (a)z轴上的声压分布;(b)不同变幅杆半径下空化体积分数Fig.5.(color online)Comparison of sound fi eld in water under di ff erent frequency ultrasounds:(a)Sound pressure distribution on z-axis;(b)cavitation volume fraction under di ff erent horn radii.

图6 (网刊彩色)不同频率超声作用下水中流场的比较 (a)平均流速随变幅杆半径的变化规律;(b)最大流速随变幅杆半径的变化规律Fig.6.(color online)Comparison of flow fi eld in water under di ff erent frequency ultrasounds:(a)The variation of mean flow velocity with horn radius;(b)the variation of maximum flow velocity in water with horn radius.

3.3 流场的测定结果

20 kHz频率超声作用下水中流场分布的实验和模拟结果比较如图7所示.其中,M和N分别表示数值模拟和实验中漩涡出现的位置.由图可知,漩涡位置对称分布,且模拟出的流线分布与实验结果相符.另外,通过粒子图像测速技术观察到变幅杆下方水中示踪粒子的运动状态,如图7(a)所示.其中白色斑点为示踪粒子.比较变幅杆下方3 mm处(即图7(a)和图7(b)中的KL段,|KL|=20 mm)实验和数值计算的流速分布,如图7(c)所示.可以看出,实验测定和数值模拟的结果十分符合,沿KL段的流速均呈现先上升后下降的趋势,且流速最大值均出现在r=5.2 mm附近,从而验证了计算结果的可靠性.

图7 (网刊彩色)实验测定与数值模拟结果的比较(a)20 kHz超声作用下水中的流场分布;(b)变幅杆下方流场分布;(c)KL线段上实验测定与数值模拟的流速Fig.7.(color online)Comparison of experimental and numerical results:(a)The distribution of flow fi eld in water under 20 kHz ultrasound;(b)the distribution of flow fi eld under the horn;(c)the flow velocity along the KL line.

4 结 论

以水为透明模型材料,数值模拟了20和490 kHz频率超声作用下水中的声场和流场分布,并通过示踪粒子图像测速的方法进行了实验研究,得到以下主要结论.

1)当超声频率为20 kHz时,声压沿超声传播方向呈衰减趋势;而当超声频率增至490 kHz时,声压水平提高,且沿传播方向呈周期性振荡特征;增大变幅杆半径能够使水中声压和发生空化效应的区域增大.

2)相同变幅杆半径作用下,两种频率超声在水中引发了相似的流场分布,且20 kHz超声作用下水中的平均流速均大于490 kHz超声作用下水中的平均流速.

3)实验观测了水中的流场分布特征并测定了流速,发现漩涡出现的位置和流速大小均与数值计算结果较好地符合,验证了声场和流场模型的正确性.

4)研究结果可以类比出超声在合金熔体中产生的声场和流场,从而为超声处理合金熔体过程的参数优化设计提供有益指导.

［1］Jian X,Xu H,Meek T T,Han Q 2005Matter Lett.59 190

［2］Zhang S,Yin L,Fang N 2009Phys.Rev.Lett.102 194301

［3］Zhao F Z,Zhu S Z,Feng X H,Yang Y S 2015Acta Phys.Sin.64 144302(in Chinese)［赵福泽,朱绍珍,冯小辉,杨院生2015物理学报64 144302］

［4］Zhai W,Hong Z Y,Wei B B 2007Sci.China Ser.G37 367(in Chinese)［翟薇,洪振宇,魏炳波 2007中国科学G:物理学力学天文学37 367］

［5］Chen R,Zheng D,Guo J,Ma T,Ding H,Su Y 2016Mater.Sci.Eng.A653 23

［6］Bang J H,Suslick K S 2010Adv.Mater.22 1039

［7］Zhai W,Hu L,Geng D L,Wei B B 2015J.Alloy.Compd.627 402

［8］Huang H J,Xu Y F,Shu D,Han Y F,Wang J,Sun B D 2014Trans.Nonferrous Met.Soc.China24 2414

［9］Gerold B,Glynnejones P,Mcdougall C,Mcgloin D,Cochran S,Melzer A 2012Appl.Phys.Lett.100 391

［10］Zhai W,Wei B B 2015Mater.Lett.138 1

［11］Dijkink R,Ohl C D 2008Appl.Phys.Lett.93 254107

［12］Muller P B,Bruus H 2015Phys.Rev.E92 063018

［13］Loh B G,Lee D R,Kwon K 2006Appl.Phys.Lett.89 2367

［14］Zhai W,Liu H M,Hong Z Y,Xie W J,Wei B B 2017Ultrason.Sonochem.34 130

［15］Tzanakis I,Lebon G S,Eskin D G,Pericleous K A 2017Ultrason.Sonochem.34 651

［16］Trujillo F J,Kai K 2011Ultrason.Sonochem.18 1263

［17］Kojima Y,Asakura Y,Sugiyama G,Koda S 2010Ultrason.Sonochem.17 978

［18］Tzanakis I,Lebon G S,Eskin D G,Pericleous K A 2017Ultrason.Sonochem.34 651

［19］Dahlem O,Reisse J,Halloin V 1999Chem.Eng.Sci.54 2829

［20］Xu Z,Yasuda K,Koda S 2013Ultrason.Sonochem.20 452

［21］Wu J,Du G 1993Ultrasound Med.Biol.19 167

［22］Aanonsen S I,Barkve T,Tjøtta J N,Tjøtta S 1984J.Acoust.Soc.Am.75 749

［23］Nightingale K R,Trahey G E 2000IEEE Trans.Ultrason.Ferr47 201

［24］Cheng J C 2012Acoustics Principle(Beijing:Science Press)p828(in Chinese)［程建春2012声学原理(北京:科学出版社)第828页］

Acoustic fi eld and convection pattern within liquid material during ultrasonic processing∗

Wu Wen-Hua1)Zhai Wei1)†Hu Hai-Bao2)Wei Bing-Bo1)
1)(School of Natural and Applied Sciences,Northwestern Polytechnical University,Xi’an 710072,China)
2)(School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China)

When ultrasound propagates in a liquid alloy,nonlinear e ff ect takes place such as cavitation e ff ect and acoustic streaming,which accelerates the solute and thermal transportation during alloy solidi fi cation,and consequently,improves the solidi fi cation microstructures and mechanical properties of the metallic alloy.Therefore,it is signi fi cant to investigate the ultrasound propagation characteristics in liquid.Here,by choosing water as a model transparent material,the acoustic fields and flow fi elds induced by 20 and 490 kHz ultrasounds are investigated by numerical simulation,and the e ff ects of frequency and ultrasonic horn radius are studied.Firstly,the simulation results demonstrate that the sound pressure under 20 kHz ultrasound decreases obviously along the ultrasonic propagation direction,and the maximum of sound pressure value is equal to the initial pressure.In this case,the cavitation e ff ect only occurs in the region close to the ultrasonic horn.By contrast,when the ultrasonic frequency increases to 490 kHz,the sound pressure is higher than that of 20 kHz ultrasound,and displays periodical vibration characteristic along the wave propagation direction.The cavitation volume correspondingly expands to a large extent with a regular striped distribution.It can also be found that increasing the ultrasonic horn radius under 20 and 490 kHz ultrasounds can e ff ectively promote the sound pressure level in water,and hence leads to the remarkable enlargement of cavitation volume.Secondly,the calculated results of flow fi eld indicate that the streamlines in water are similar under the two ultrasounds with di ff erent frequencies.A jet produced by the center of horn spreads down and divergences to both sides after reaching the bottom.For both frequencies as the horn radius increases,the radius of jet increases and the average velocity in water fi rst increases and then decreases,whose maximum value appears when the horn radius is 40 mm.Meanwhile,the average velocity under 20 kHz ultrasound is larger than that under 490 kHz ultrasound for each horn radius.Finally,particle image velocimetry method is employed to measure the velocity fi eld in water.Both the positions of eddy and the velocity distribution are the same as the simulation results,which veri fi es the reliability of the present theoretical calculation model.The scenario in this work is analogous to the acoustic fi eld and the flow fi eld in liquid alloy,which is bene fi cial for the design of parameter optimization during ultrasonic processing in alloy solidi fi cation.

ultrasound,acoustic fi eld, flow fi eld,cavitation e ff ect

27 January 2017;revised manuscript

15 July 2017)

(2017年1月27日收到;2017年7月15日收到修改稿)

10.7498/aps.66.194303

∗国家自然科学基金(批准号:51327901,51571164)、陕西省科技新星项目(批准号:2016KJXX-85)和陕西省科技统筹创新工程重点实验室项目资助的课题.

†通信作者.E-mail:zhaiwei322@nwpu.edu.cn

©2017中国物理学会Chinese Physical Society

PACS:43.35.+d,47.35.Rs,02.60.Cb,81.20.–n

10.7498/aps.66.194303

*Project supported by the National Natural Science Foundation of China(Grant Nos.51327901,51571164),Shaanxi Province Science and Technology Star Project(Grant No.2016KJXX-85)and Shaanxi Province Science and Technology Innovation Project Key Laboratory Project,China.

†Corresponding author.E-mail:zhaiwei322@nwpu.edu.cn