统计学方法在上市公司股利分配中的应用

吉云峰

作为上市公司的核心财务问题之一，股利的分配（股利政策）不但关系到股东和债权人等利益相关者的利益，又与企业未来的发展紧密相连。因此，以合理的股利政策，协调股东和企业之间的利益分配就成为上市公司应当重点考虑的问题。而在上市公司股利分配的过程中，统计学方法得到了越来越广泛的应用。

一、研究上市公司股利分配的意义

1.股利政策不稳定。一般而言，越是成熟和发达的资本市场，上市公司采取稳定的股利政策的可能性就越高。这是因为我国市场机制还不健全，各项监管制度并不完善，致使上市公司的股利政策缺乏稳定性，具体表现为股利支付率和股利分配形式的频繁变动，连续性难以保证，长期的股利分配计划严重缺失。

2.派现水平低。从近几年各上市公司公布的年报看，尽管其盈利水平都获得较大水平的提高，但在对股东的回报方面显得极为“吝啬”。据上交所统计，沪市上市企业拟进行股利分配的占比不到半数，现金红利总额占上市公司净利润总额比例在20%左右。

3.不分配现象严重。我国上市公司不分配股利已经成为比较普遍的现象，即使证监会出台了再融资与派现相关的导向政策以后，股利不分配现象仍然严重。目前，我国企业上市后从未进行股利分配的有200多家，其中近半数从未进行过利润分配。

二、统计方法在上市公司股利分配中的典型应用

对上市公司股利分配进行研究的方法一般分为统计类与非统计类两种不同种类。统计类方法涉及回归分析、方差检验、因子分析、相关分析等；非统计类方法涉及递归划分算法、实验法和观察法以及预测法等多种方法；此外，还有综合分析法、行业分析法、模型分析法等。在统计学方法体系里，又可把它们分成参数统计和非参数统计两类。其中，参数统计方法一般借助一定的标准对选取的指标构建相关模型，借此对统计对象划分成不同的类别。而非参数统计方法涉及K-最近邻法、DEA法和聚类分析方法等。下面对上市公司股利分配中能够用到的主要的统计方法进行阐述。

1. 回归分析。上市公司股利分配中多使用的回归分析有多元线性回归和TobitⅡ线性回归两种类型。在多元线性回归中，一般以逐步回归法对现金股利政策的影响因素进行分析。

2.方差检验。传统的统计描述虽然能够反映上市公司股利分配的基本特征，但这种分析显然不够严格。因此，应该在讨论分配方案的过程中，对市场反应的差别进行检验，看其超额收益率是否达到了显著水平。具体做法是对各种分配方案进行计算，分析平均超额收益率的水平和t值。比如，在一定的显著性水平上，现金分红和混合分配方案通过了检验，但是不分配和单一的转增股本与市场分配综合未能达到这一点，就说明唯有现金分红和混合分配才能对公司股价的运行产生显著影响。更为重要的是，现金分红信息的影响并非是正面的，它会产生部分程度上的折价，但是混合分配信息的影响却是正面的，它能够产生不同程度的溢价。

因为投资行为会反映投资者在收益率与风险之间的选择，因此单一从收益率的角度分析考察股利分配就有片面。为了做进一步的验证，应该知晓在不同分配政策中，超额收益率的方差是不是有显著差别，由于方差的差异性可以反映出投资者对部分股利分配政策的喜好。为此，要对不同分配方案的超额收益率方差进行显著性检验，判断投资者偏好对证券市场的影响。检验过程与内容以两部分完成：第一部分指的是Levenes方差齐次性检验，此时在于判断方差总体的一致性。如果分配方案的F 检验值和显著性概率均小于一定水平，则说明在特定的显著性水平上，不同组之间的总体方差存在显著差异，否则就说明两两分组中总体方差并不存在显著差异；第二部分会给出不同组所在总体的方差一致性以及方差不相等时的T检验结论，然后按照第一部分的方差齐次性检验结果进行判断。

为了比较不同分配方案之间在股票價格影响方面的差异，需要确认股利分配信息会不会对股价产生明显影响，可以继续通过单因素方差分析法进行判别。若判别出F值和显著性概率都小于特定的显著性水平，则说明现有分配方案中有显著差别。进一步得出详细的结论，可以使用Tamhanes T2多重检验分析法进行判别，如果部分分配方案之间的比较能够通过特定水平的显著性检验，而其他无法通过，则表明无法判别不同分配方案之间是否存在显著差别。这样，不但能够考察证券市场对不同分配方案的反应，检验方法之间也可以进行相互验证。

3.因子分析。在应用因子分析法对上市公司的股利分配问题进行研究时，应该对变量加以标准化处理，继而进行KMO与Bartletts检验，目的在于对是否适合因子分析进行检验。如果KMO测度大于0.5，则表明原始数据能够进行因素分析，再计算Bartletts检验值、自由度和Sig.，倘若Sig.值处在特定的显著水平，就代表总体的相关矩阵之间有共同因素存在，此时运用因子分析法是适合的。其次，应确定因子个数与因子解的个数。在借助主成分分析对初始因子进行求解的过程中，特征值应处在某种程度上，并将其视为主成分影响力度大小的关键指标。通常情况下，特征值不小于等于1是其纳入标准，而舍弃特征值小于1的主成分，因为倘若特征值达不到要求，就说明该主成分的解释力度不如引入其他原变量，不如舍弃。接下来确定因子个数（m个）并计算因子值。因子值是观测变量的加权平均，求解过程要通过观测变量的线性组合表示，相应表达式为：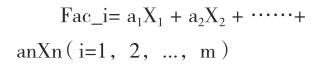

该式中，需要考虑董事长持股比例、总经理持股比例、高管人员持股比例、第一大股东持股比例、监事会持股比例等公司治理变量，以及公司股权集中度、激励、监事会的规模、实际控制人类别、治理透明度、董事会规模、独立董事比例等因素。

三、统计方法在上市公司股利分配中的进一步应用

除上述所列的回归、方差分析和因子分析等典型方法外，在上市公司股利分配中得到应用的统计学方法还有很多。比如，时间序列分析、马尔科夫链、神经网络，决策树、专家决策系统、模糊综合评判、进化算法、粗糙集、支持向量机（SVM）、多目标决策等。其中的任何一种方法都存在进一步发掘的空间，即在对统计学方法进行应用时，可以根据分析的需要向前和向后继续进行，这样有可能会得到更加有价值的信息。比如，在方差检验之前，可以利用SPSS、 MINITAB等软件得到样本数据的基本统计量，并通过标准差和不同分配方案引起的平均股价的变化率等，初步考察证券市场对股利分配方案差异性的偏好；或者在回归分析的基础上，进一步计算每股股利与净资产收益率、每股收益、每股留存收益、每股未分配利润、货币资金的比例之间的相关系数，如果在特定的显著性水平下显示为显著正相关，且相关系数较大，将能够进一步验证回归分析的结论；或者在进行因子分析或回归分析的同时，结合主成分分析进行同步的相互验证，通过计算标准化数据的相关系数矩阵、特征值与特征向量等，判断提取出主成分的个数和种类，最后使用因变量现金股利相关数据对主成分分析所得的因子进行逐步多元线性回归，将所得因素进入了回归方程进行自变量与因变量显著线性相关关系的检验。

这些方法在使用的过程中会出现不同程度上的约束。比如，模型的不同对应着需要不同的前提条件，但在实际操作中，这些条件却难以满足全部上市公司，因此，在实际应用中不但要根据具体情况进行有针对性的选定和使用，必要时还应该将多种方法结合使用，这样才能最大限度提高统计学方法在上市公司股利分配中的应用价值。（作者单位：南阳泰诺联合会计师事务所）