化繁为简不走寻常路——例谈解析几何中转化与化归思想的巧用

薛 梅

(江苏省如皋市第二中学，江苏 如皋 226575)

化繁为简不走寻常路
——例谈解析几何中转化与化归思想的巧用

薛 梅

(江苏省如皋市第二中学，江苏 如皋 226575)

解析几何是高考的重点、热点和难点，因综合性强、计算量大而让很多考生望而生畏.本文将转化与化归思想巧妙融入解析几何的解题中，提出三种方法，让学生能够化繁为简不走寻常路，巧解题，少用时，多拿分.

转化与化归思想；高中数学；解析几何

解析几何是高中数学的重点，是高考命题的热点，同时也是学生解题的难点.笔者结合平时教学，总结出转化与化归思想在解析几何解题中的三种常用方法，让学生解题时能化繁为简不走寻常路.

一、注重数形变换，巧用“数”与“形”的转化与化归

我们研究解析几何时常用代数方法来处理，但会遇到计算繁杂、费时耗力、容易出错、难得结果等情况，这时我们引入转化与化归思想，进行“数”与“形”的有机转化，巧妙地将解析几何问题转化成平面几何问题去处理，就能使解题变得简单上手.恰如著名数学家华罗庚所讲“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休”.

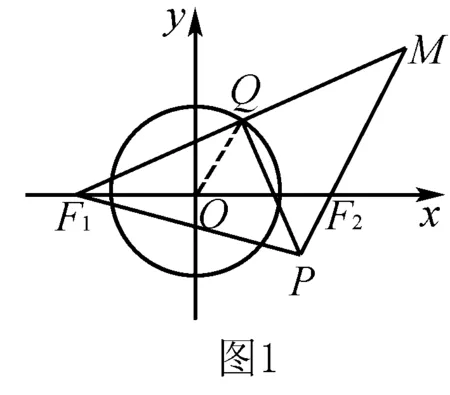
例1Q为圆x2+y2=1上任意一点，已知两个定点F1(-2,0)、F2(2，0)，F1关于Q的对称点是M，线段MF1中垂线与MF2相交于P点，求P点轨迹.

解析如果假设Q点坐标，代入圆方程进行计算则比较麻烦，如果运用数形结合思想，把问题转化为几何问题，此题就变得容易解决.

连接OQ,O是F1F2中点,O是MF1中点,所以OQ∥MF2，MF2=2即|PM-PF2|=2,因为P为线段MF1中垂线上一点，所以PF1=PM,所以|PF1-PF2|=2，又因为F1,F2为两定点，且|F1F2|=4>2,由双曲线定义易知P点轨迹是双曲线.

二、注重角色变换，巧用“动点”与“定点”的转化与化归

“动静结合”是道家研习武学的至高境界之一，而在高中数学解题中也常会用到一种与之类似的思想方法，叫做“动定结合”，通过同一对象在动与定角色间的不断转化，巧妙破解难题.就像在解析几何中，动点和定点往往不是固定而是相对的，对于同一对象可根据解题需要变换动点与定点“角色”，特别是在处理含有多个动点问题时，可先将一个动点视为定点，得出相关结论后，再考虑其是动点的问题，这样通过动点与定点的相互转化，就能使问题找到解决办法.

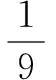
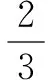
三、注重方程变换，巧用“普通方程”与“参数方程”的转化与化归

近年来，求解极值和取值范围问题是高考解析几何中的常见题型，这类题目知识面广、综合性强、新颖度高、难度也较大，因能很好地考查学生的数学思想和数学思维，一直受到命题专家的青睐.考生在处理这类题目时，如果抓不住关键而用普通方程就题解题，便会落入复杂计算的“陷阱”不能轻易“脱身”.其实，解答这类题目，我们应采用转化与化归思想，对题干进行适当的加工、改造和变化，使之变得简洁、明了和熟悉，将运算复杂的普通方程转化成便于化简的参数方程，从而省时省力事半功倍.

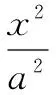
(1)求m的值和椭圆方程；

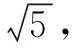
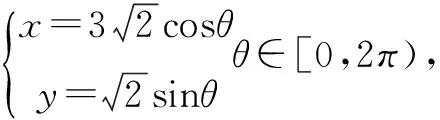
美国著名教育和心理学家布卢姆指出：数学转化与化归思想是“把问题元素从一种形式向另一种形式转化的能力”.因此，高中数学教师在平时的教学中要注重渗透转化与化归思想，有意培养转化与化归思维，着力引导转化与化归解题，让学生通过巧妙的变换，拨云见日，化繁为简不走寻常路，找到答题的“终南捷径”，从而使转化与化归思想成为解析几何的破题之法、解题之术、拿分之招.

[1]赵雪妍.向量在解析几何中的应用[J].中学生数理化(高中版·学研版)，2011(05).

[2]袁辉.运用化归思想，培养有效思维[J].数理化学习(高中版)，2011(09).

G632

A

1008-0333(2017)22-0044-02

2017-06-01

薛梅(1981.11-)，女,江苏省南通市，大学本科，中学一级，从事数学学科教学与研究.

责任编辑：杨惠民]