追本溯源 关注教材——对两道高考填空题引发的思考

张路民

(南京市大厂高级中学，江苏 南京 210044)

追本溯源关注教材
——对两道高考填空题引发的思考

张路民

(南京市大厂高级中学，江苏 南京 210044)

对2016年的江苏高考试题作了细致的研究，试题注重基础知识和通性通法的考查，同时试题也提醒我们要关注课本.高考中有相当一部分试题来自于课本中的小问题，来源于课本例题与习题变形的大问题，在高三复习中要真正认识到回归课本的重要性.

高中试题；通性通法；回归课本

认真研究了2016年的江苏高考试题，总体来说试题难度不大.虽然对这份试题或多或少的存在着一些争议，但试卷重视对数学应用意识和创新意识的考查，试题设置注重应用性和探究性，能够较好地考查学生的知识迁移水平和综合运用所学知识分析问题、解决问题的能力，这点是毋庸置疑的.其中笔者比较感兴趣的是第13题和第14题.下面就这两道题谈一些想法.

一、注重通性通法的应用，关注各地典型模拟题

数学中有许多通性通法，在平时的学习中如能适时地加以归纳总结，对于拓展解题思路，快速地解决问题有很大的帮助.

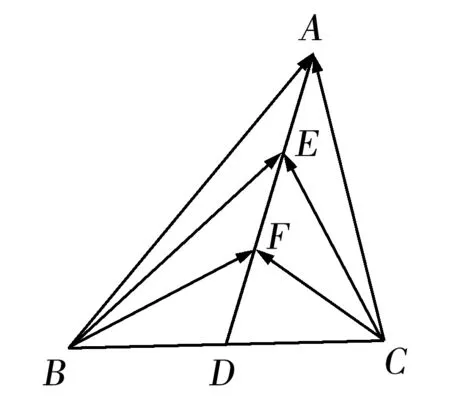
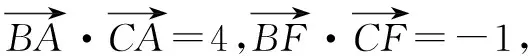
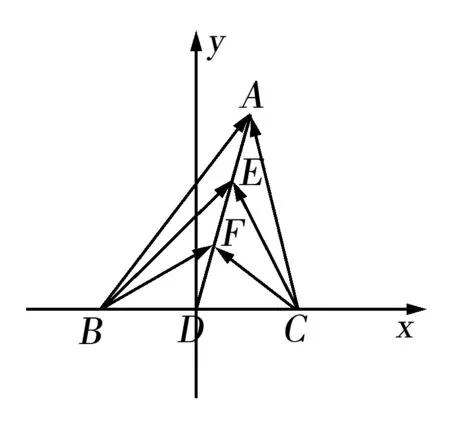
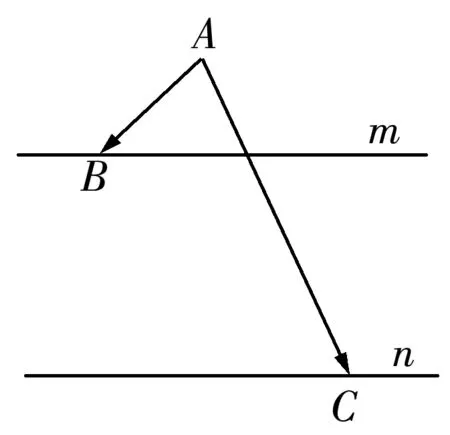
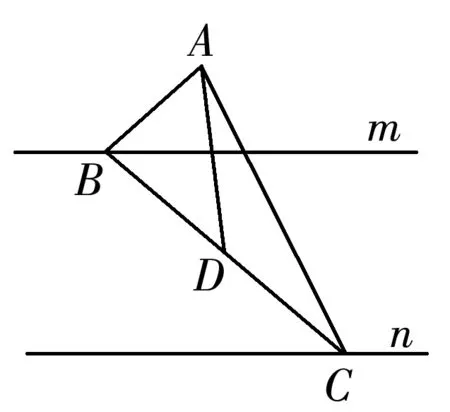
分析向量的数量积是向量中的重要知识点，也是江苏高考的C级考点.而数量积问题的解决也有通性通法，一般较简单的问题用定义即可解决，稍复杂的可以建立适当的直角坐标系或采用基底法，再难点的则要进行适当的转化.本题直接用定义不能解决，故可以尝试建立直角坐标系和基底法解决问题.

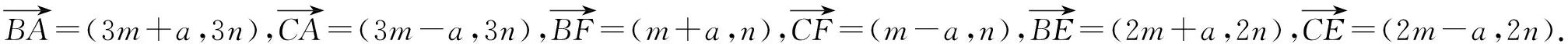
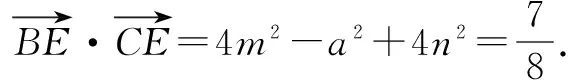
解法二(特殊化法)结合题意，本题的最终结论跟线段BC和AD的长度有关，但跟△ABC的形状无关.因此不妨假设△ABC为等腰三角形，且BC=2a,AD=3h.

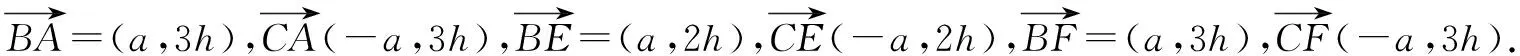
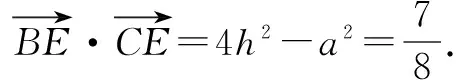
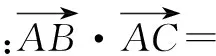
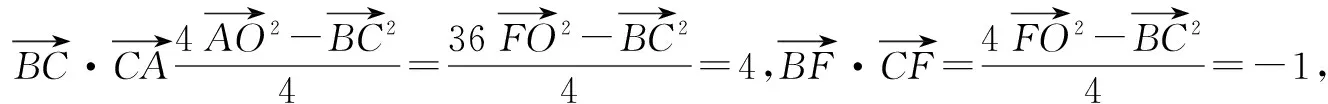
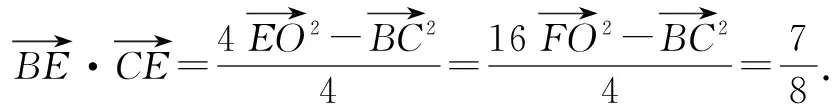
应用1 (南京市2016届高三第二次模拟第11题改编)在△ABC中，A=120°，AB=4，AC=2若点D为边BC的中点，则AD的长为____．

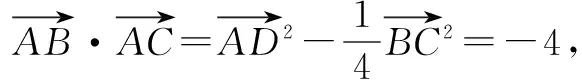
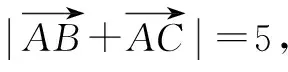
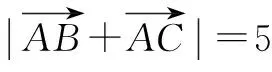
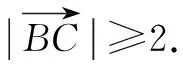
二、适时回归课本，重视典型例题

课本是学生学习数学的第一手资料，高考中有相当一部分试题来自于课本中的小问题，但是有些学生却不能正确处理，以至于在高考中出现大问题. 另外，高考试题中来源于课本例题与习题变形的大问题，也不少见.因此，要使学生在知识的海洋中如鱼得水，在高三复习中就必须真正认识到回归课本的重要性.

例题2 (2016年江苏高考试题第14题)在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是 .

知识链接(苏教必修四P116页的例题4)在斜三角形ABC中，求证：tanAtanBtanC=tanA+anB+tanC.

分析这是一道非常经典的三角恒等变换问题，学生如能做有心人记得此结论对于例题2的解答会大有帮助.(证明略)此外，该问题在课本中还有很多类似的变形.

变形1 (苏教必修四P117页的练习2)求证：tan3α-tan2α-tanα=tan3αtan2αtanα.

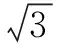
变形3 (苏教必修四P118页的习题8)求证：tan(A-B)tan(B-C)tan(C-A)=tan(A-B)+tan(B-C)+tan(C-A).

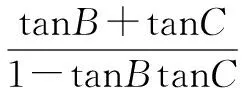
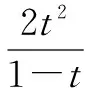
小结比较两种解法显然方法一要简洁得多，而且思路清晰.因此关注课本例题，习题和一些常规结论对于顺利解题会有很大帮助，甚至能起到事半功倍的效果.

拓展改编1 在锐角三角形ABC中，若sinA=2sinBcosC，求tanAtanBtanC的最小值.

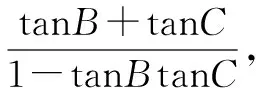
拓展改编2 在三角形ABC中，角B为不小于30°的锐角，若cosA=2sinBsinC，求tanA+tanB+tanC的取值范围.

解析在三角形ABC中由cosA=2sinBsinC可知角B,C不为直角又cosA=-cos(B+C)=-cosBcosC+sinBsinC=2sinBsinC即-cosBcosC=sinBsinC可得tanBtanC=-1.

因此tanA+tanB+tanC=tanAtanBtanC=-tanA.

总之，对于高三阶段的复习而言，回归课本、紧扣课本、吃透课本是应付高考的重要的方法，也是最佳的办法. 高考题源于课本，所涉及的知识点都在课本中，有些不起眼的例题，习题在高考中也能做大文章.在高三复习中，教师一定要坚持回归课本，以本为本，吃透教材，抓住数学本质，同时也要关注各地的模拟试题，对于一些典型的试题多加研究探讨，找到一些通性通法，能够启发学生拨开云雾见真谛，提高解题效率，从而帮助学生脱离题海，取得更加优异的高考成绩.

[1]单墫.普通高中课程标准实验教科书·数学4(必修)[M].南京：江苏教育出版社，2012.

[2]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003.

G632

A

1008-0333(2017)22-0003-03

2017-06-01

张路民 (1977-)，男，江苏南京人，中学高级教师，主要从事高中数学解题与课堂教学研究.

责任编辑：杨惠民]