三角函数求值问题的教学“纠错”实录
陈建邦 侯 军
(1.云南省石屏县第一中学,云南 662200;2.云南省红河州石屏高级中学,云南 662200)
三角函数求值问题的教学“纠错”实录
陈建邦1侯 军2
(1.云南省石屏县第一中学,云南 662200;2.云南省红河州石屏高级中学,云南 662200)
三角函数是高考的热门考点,在高中数学教材中占有重要的地位.教学中,我们发现学生在解三角函数问题时,经常出现漏解、增解、错解的现象,其根本原因是对题设条件中的隐含条件挖掘不够.本文以此为出发点,展示教师如何引导学生自主挖掘三角函数题目中的隐含条件,掌握更多的解题思想,进而达到提高学生数学解题能力的目的.
错解;三角函数求值;隐含条件
一、教材分析
三角函数与解三角形等知识在新课标人教A版的教材的必修四第一、三章,必修五第一章.从课程的设置和安排上就可以看出三角函数的重要性,必修一用集合的观点来定义函数,后续学习了函数的性质,但是没有具体的函数模型来认识函数的性质.学习了幂函数、指数函数、对数函数这些具体的函数之后,学生对定义域、值域、单调性有了深刻的认识,通过对三角函数的学习,进一步深化学生对函数的理解,它不仅体现了函数的通性,也涉及到了诸如整体代换、数形结合、分类讨论等基本数学思想.这也无形中确立了三角函数在高中数学教学中的重要地位.
二、问题提出
在涉及三角函数求值问题时,学生普遍有两大问题,第一,公式记不住或者记忆混淆.第二,不能很好地判断或分析角的范围.对于第一个问题普遍是学生懒惰造成的,第二个问题确实是个难点,也是对教师的挑战.我们知道,三角函数求值问题类型主要有三类:
(1)“给角求值”问题:主要是公式的应用.
(2)“给值求值”问题:解题的关键在于变角,注意角的拆分.
(3)“给值求角”问题:实质上是转化为“给值求值”问题,关键也是变角,把所求角用含已知的式子表示,由所得的函数值结合该函数的单调区间求得角.但是解三角函数问题,不管用什么方法,都要首先明确角的范围以及角所在的象限.
三、问题探究
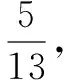
1.错解展示
学生A的解答过程是这样的:
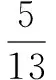
cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB.
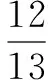
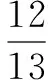
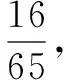
2.正解解析
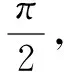
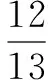
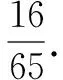
方法三(学生小组讨论后的解答)由△ABC中大角对大边以及正弦定理可以得到
若A>B⟺sinA>sinB,应用这个关系可以判定该题的sinA 易得A为锐角,很容易得正确答案. 还有没有其他解答方法呢?(教室安静) 教师补充解答: 方法四∵0 cosA>cos(π-B)⟹cosA+cosB>0. 我们可以得到这样的结论:在△ABC中,cosA+cosB>0. 学生出现错解的主要原因是他们在解题时没有注意角的范围.故教师在进行这部分内容的教学时应着重培养学生的“重视角的范围”的解题意识. 学生甲的解答: 教师给出解答: 看来答案只有一个,那这是为什么呢?学生的方法怎么改进才能正确呢?经教师引导,学生仔细思考后,部分同学的回答是这样的: ∵sin2θ>0,cos2θ<0,∴2θ是第二象限的角,则θ是第一、三象限的角,所以tanθ>0所以tanθ=2.这道题让学生深刻地感受到挖掘隐含条件明确角的范围对三角函数值的影响. 学生乙的解答是这样的: 正确的解答如下: 数学解题要注意观察、分析问题的数学表征,然而许多学生在观察问题时,往往把注意力集中在显性条件上,只要求解符合思维逻辑,就盲目地下结论.所谓差之毫厘谬以千里.挖掘题目中的隐含条件,既是数学解题的一项基本功,也是培养学生的思维品质的重要手段.建构主义的学习理论告诉我们“学习过程不是学习者被动地接受知识,而是积极主动地建构知识的过程”.在课堂教学中,教师遇到学生的错解不妨“等一等”,给学生充分的思考时间,让学生通过集体讨论、自主探究一点点地发现问题所在,教师再启发诱导,给出完美的答案,这才更符合学生的认知规律. [1]同济大学数学系.高等数学[M].北京:高等教育出版社,2007. [2]人民教育出版社等.普通高中课程标准试验教科书(必修)数学4(A版)[M].北京:人民教育出版社,2014. G632 A 1008-0333(2017)22-0022-02 陈建邦,中学一级,石屏县第一中学,主要从事高中数学教学和初等数学研究工作.侯军,中学一级,石屏高级中学,主要从事高中数学教学和初等数学研究工作. 责任编辑:杨惠民]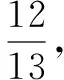
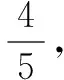
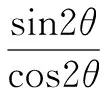
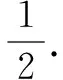
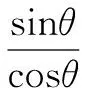
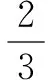
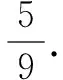
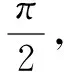

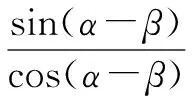

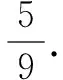
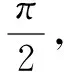
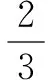


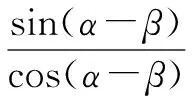
四、反思总结

