正难则反思想在高中数学解题中的应用

孙 硕

(江苏省射阳县第二中学，江苏 盐城 224300)

正难则反思想在高中数学解题中的应用

孙 硕

(江苏省射阳县第二中学，江苏 盐城 224300)

古有孙子兵法中的欲擒故纵，现有数学求解中的正难则反，这两者有着异曲同工之妙.纵观高中数学知识点，正难则反思想涵盖以下几个知识点：(1)集合求解中的补集思想；(2)概率计算中的对立事件；(3)数学证明中的反证法思想.在本文中，我们将结合实际习题，对正难则反思想在高中数学解题中的应用进行讨论.

高中数学；正难则反；数学思想

一、集合问题中的正难则反

集合问题考查的是学生的逻辑思维能力，需要学生对需要计算的集合模型具有清晰的思路.对于某些集合问题，从正面求解往往极其复杂，思路不明朗，需要考虑很多影响因素，且极容易出错.此时，我们不妨使用补集的思想，通过补集反演出欲求的结论，实现简化求解的目标.

例1 已知集合A={x|x2-4mx+2m+6=0}，集合B={x|x<0}，若是A∩B≠∅是假命题，试求m的取值范围.

思路分析由A∩B≠∅可知，集合A中至少有一个正根，由于存在x与m两个未知数，若是细分较为繁琐.此时，不妨利用正难则反的思想，利用原命题补集进行求解，即是关系式A∩B=∅，则集合A只有无根和有两个非负根这两种情况，较为容易分析.

二、对立事件中的正难则反

在事件判断时，若事件A成立时存在多种情况，难以进行分析计算.此时，可以尝试利用其对立事件进行判断.尤其是碰到至多、至少、唯一、无限等词眼时，需要机智想到正难则反思想在对立事件中的运用.如果正向判断存在多种可能时，即可从其对立事件出发，转换一下思维角度，从提问或设问的对立事件入手.值得注意的是，在给出最终结论时，必须注意将原事件与对立事件进行转换，切忌功亏一篑.

例2 已知事件A：关于x的方程x2+4ax-4a+3=0、x2+(a-1)x+a2=0、x2+2ax-2a=0中至少有一个方程有实数根，若事件A成立，求实数a的取值范围.

思路分析将上述例题中至少有一个方程有实数根的命题视为原命题，则从原命题角度出发，上述三个方程至少存在一个方程存在实数根的情况存在多种可能性，几乎难以一一分析.此时，我们可以利用正难则反思想，从其对立事件考虑，即上述方程均无实数根，再求实数a的取值范围.

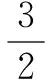
三、反证法中的正难则反

根据正难则反的原理，当从正向求证过于困难时，或者正向求证存在多种讨论情况时，我们即可从反证中寻求思路突破.反证法不仅是运用在几何知识中，在代数证明中也较为常见.如能运用得当，对简化求解过程、提高求解准确率作用显著.

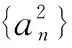
思路分析本题求证存在无穷多项为无理数，若是从正向求证，我们难以一一罗列出所有的无理数.且就算可以描述无理数，也必然需要大量的文字描述，违背了数学训练的初衷.对此，我们不妨从反证法的角度，假设数列{an}的项都是有理数，并推出矛盾即可得证.

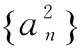
总之，正难则反的思想是一种极其重要的数学思想，是一种出奇制胜的秘密武器.在高中数学解题中，正难则反思想有着广泛的运用，在函数、方程、数列、几何等知识点中均有其身影.本文仅仅从三个极小的训练题对正难则反思想进行讨论，欲将其渗透到学生解题思维中，还需要一线教师更多的努力.

[1]周庆东.正难则反——谈逆向思维带来的启迪[J].高中数理化，2017(Z2).

[2]张金华.正难则反——巧用补集思想解题[J].高中数理化，2007(03).

G632

A

1008-0333(2017)22-0032-02

孙硕(1976.08- )男，江苏盐城人，本科学历，中学一级教师，主要从事高中数学教学与研究.

责任编辑：杨惠民]