含参不等式恒成立问题的解题技巧

潘素梅

(安徽省阜阳市临泉第一中学，安徽 阜阳 236400)

含参不等式恒成立问题的解题技巧

潘素梅

(安徽省阜阳市临泉第一中学，安徽 阜阳 236400)

由于含参不等式恒成立问题具有灵活多变，综合性强和知识点涵盖多等特点，一度成为学生们取得高分的绊脚石.含参不等式恒成立问题技巧性较强，因此，正确的解题思路和解题技巧，至关重要！

高中数学；恒成立问题；解题技巧

高中数学中，含参不等式恒成立问题多以函数、三角、解析几何以及导数等作为载体，相互转换，综合性比较强，相应的解法也是多变的，技巧性也相对比较强.学生们只要学好这些方法与技巧，灵活运用，就如同行云流水般，便可巧妙地化解含参不等式恒成立问题.因此解决含参不等式恒成立问题的关键就在于函数、数形结合以及化归与转化思想的运用.

一、变换主元，构造函数

有时候，学生们在做题时，经常会遇到一道题中有许多变换的元，想要试求去消元，结果无功而返.这时候学生们可以转换思路，看看是否可以选取其中某一个变换的元作为主元，同时将其他变换的元就看作常量，这时候就可以简化解题的过程，从而达到一种减元的效果，转化成自己熟悉的题型，可谓是“柳暗花明又一村”！

例1 已知a∈[-1,1]，不等式x2+(a-4)x+4-2a≻0恒成立，求x的取值范围.

解析由题意，可以知道，该题是一道关于含参不等式恒成立的问题，仔细观察，可以把不等式左边看成关于a的一次函数，记作f(a)=(x-2)a+x2-4x+4，则f(a)>0在a∈[-1,1]上恒成立，故{f(-1)>0f(1)≻0，代入化简解得x<1或x>3，即x的取值范围是(-,1)∪(3,+).

点拨在解含参不等式恒成立问题时，学生们要清晰地认识参数与未知数之间的关系，要能轻松地将关于x的不等式转换为关于参数的不等式.本题中关键点就是将不等式左边转换成关于a的一次函数，再根据条件，求解x的取值范围.这两者之间互相制约，互相依赖！

二、数形结合，巧求参数

在含参不等式恒成立问题的求解过程中，光凭借代数之间的转换，有的时候只能解决其中的一些问题，还有的问题依靠代数的转换可能就变得越来越复杂，这时候，如果学生们能画出相对应的图象关系，反而会更巧妙的求解出答案，因此，“数形结合”思想，也是求含参不等式恒成立问题的一把金钥匙！

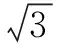
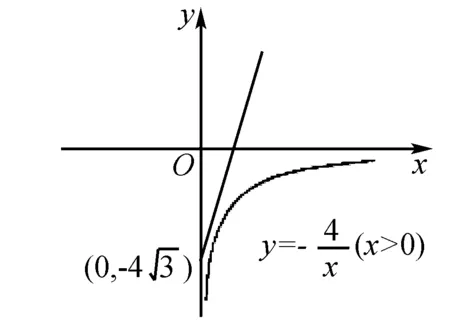
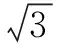
综上所述，存在实数k∈[3,+)使得关于x的不等式4-kx-≤0在x>0恒成立.

点拨本题中运用“数形结合”的思想，更加清晰明了，直观地看出了函数间的节点，就可以获得对应的数量关系，是解本道题的关键所在.因此，学生们在解含参不等式恒成立问题时，要准确无误地画出函数的图象关系，找到节点，方能给解题打开思路，同时运用“数形结合”可以简化思路，提高题解效率.

三、构造函数，巧求最值

在遇到求最值的问题时，学生们要想到构造函数的思想，通过构造出的新函数，找出数量关系.构造函数求最值一般有两种方法：一是分离参数法；二是利用二次函数性质.

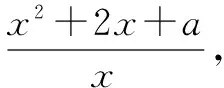
解析由题意易知，x2+2x+a≻0恒成立，故a>-(x2+2x)恒成立，x∈[1,+).此时可以看出是二次函数，可以设g(x)=-(x2+2x)，整理之后可以知道g(x)在x∈[1,+)上单调递减，故g(x)max=g(1)=-3，即a>-3，因此实数a的取值范围是a∈(-3,+).

点拨此题看似很短，可是涉及到的知道点很多，如果脑海里没有构造函数的想法，对于解这道题是比较难的.前面讲到分离参数法，有这样的结论：若函数f(x)有最小值，则a≤(<)f(x)恒成立⟺a≤(<)f(x)min，同理，若函数f(x)有最大值，则a≥(>)f(x)恒成立⟺a≥(>)f(x)max.

通过对含参不等式恒成立问题的分析，相信学生们受益匪浅，虽然含参不等式恒成立问题属于比较难的一类题型，但是只要掌握相应的解题技巧，灵活多变，就会不攻自破.当然本文只是对涉及到此类题型解题技巧的些许讲解，还有更多的解题方法与解题技巧，需要学生们在今后的学习中不断地探索与总结！

[1]马刚.含参不等式恒成立问题的求解策略[J].教育教学论坛,2012(12).

[2]楼建忠.问题驱动 引领探究——对“含参不等式恒成立问题”教学反思[J].中国校外教育,2015(9).

G632

A

1008-0333(2017)22-0056-02

2017-05-01

潘素梅(1982.11-)，女，安徽临泉人，中学一级教师，硕士学历，从事中学数学教育.

责任编辑：杨惠民]