研究高中数学解题中整体思想的应用

孙智斌

(山东省临沂第一中学,山东 临沂 276000)

研究高中数学解题中整体思想的应用

孙智斌

(山东省临沂第一中学,山东 临沂 276000)

数学科目是高中阶段的重要学科之一，并且高中数学知识相对复杂、难懂.所以为了能够提高数学题解题的速度与效率，本文将针对高中数学解题中整体思想的应用进行分析.

高中数学；三角形；函数；整体思想

在解答高中数学题的过程中，积极地运用整体思想，有助于提高解题的速度与准确性，改善学生自身的数学解题能力.

一、高中数学三角函数解题中整体思想的应用

三角函数是高中数学知识的重点难点，很多同学在学习该部分知识的时候都会被复杂的问题所难到.不过，只要掌握了三角函数的知识要点，在解题中充分地运用整体思想，所有的难题都会被迎刃而解.

例题1 求函数f(x)=sinxcosx/(1+sinx+cosx)的值域.

分析在该题的解答中，面对如此复杂的三角函数，我们首先应该想到的就是利用整体思想进行换元，重新构建简单的新函数，进行问题的处理.

又因为sinx+cosx=t,所以sinxcosx=(t2-1)/2 ②.

将①②式代入到f(x)=sinxcosx/(1+sinx+cosx)中进行整体换元可得：

f(x)=[(t2-1)/2]/(1+t)=(t-1)/2.

分析在该题的解答中，依旧要从整体的思想去考虑，根据该题的形式，我首先想到了奇函数与函数的对称性性质.另外，由于该题属于分式类函数，所以在解答的过程中可以对最大值与最小值进行整体处理，从而提高解题效率与准确性.

根据函数的性质可知，g(x)=f(x)-1=(x+sinx)/(2x2+cosx)是奇函数.

所以g(x)min+g(x)max=0.

然后将g(x)=f(x)-1代入g(x)min+g(x)max=0中，就可得到g(x)min+g(x)max=(m-1)+(M-1).

由此可知(m-1)+(M-1)=0,等价于m+M=2

二、高中数学函数解题中整体思想的应用

例题3 在x<0时，f(x)=x+1/x2-x-1/x的最小值为多少？

分析该题在解答中可以采用整体处理方法，将“x+1/x”作为整体，进行整体换元.

解令t=x+1/x，因为x<0，所以t≤-2.

所以f(x)=(x+1/x)2-(x+1/x)-2=t2-t-2=(t-1/2)2-9/4.

因为t≤-2，所以当t=-2的时候，函数f(x)存在最小值，且f(x)min=4.

三、高中数学几何问题中整体思想的应用

几何数学知识是高考必考重点知识，因此在数学知识的学习中必须重视几何问题的解答.由于当前数学习题多数都是由各种知识组合而成，因此要想提高几何问题的解题准确性，就必须大胆地运用整体思想.

例题4 现再已知有一个点P(x0,y0)和一条直线Ax+By+C=0，问点到直线的距离是多少？

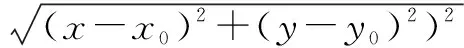
解首先，设直线l的方程为B(x-x0)-A(y-y0)=0 ①.

再把直线l的方程改写为A(x-x0)+B(y-y0)=-(Ax0+By0+C) ②.

对①②式进行整理，然后代入点到直线的公式可得

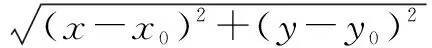
例题5 已知实数x、y满足方程x2+y2=6x-4y-9，问2x-3y的最大值和最小值的和应该是多少？

分析通过分析辨别这个方程我们可以发现，该方程属于圆的方程，在解题的过程中十分适用与整体换元法进行解题，所以可以设2x-3y=k，那么就存在2x-3y-k=0这个等式.此时可以把该等式看做是一条直线方程，那么k的最值就应该在直线与圆相切的时候才能得到.

解x2+y2=6x-4y-9整理可得(x-3)2+(y+2)2=4 ①.

然后假设2x-3y=k②.

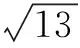
等价于k2-24k+92=0 ③.

此时2x-3y的最值分别是方程③式中的两个根.

然后根据韦达定理可以得:k1+k2=24.

所以2x-3y的最值之和就是24.

综上所述，在高中数学题解答的过程中积极地运用整体思想，不仅可以降低解题的难度，还有助于提高解题的速度与准确性，因此十分具有使用价值.

[1]高梓铭.试论如何提高数学解题速度[J].科学咨询(教育科研)，2017(01).

[2]袁双华.浅论如何培养学生数学解题的创新思维[J].科技创新导报，2016(35).

[3]石有菊.提高中职学生数学解题能力的策略[J].科学咨询(科技·管理)，2013(02).

G632

A

1008-0333(2017)22-0013-02

2017-06-01

孙智斌(2000.2- )，男，汉族，山东省临沂人，高中在读.

责任编辑：杨惠民]