圆锥曲线参数方程在高中数学解题中的应用

孙丹丹

(淮安市新马高级中学，江苏 淮安 211700)

圆锥曲线参数方程在高中数学解题中的应用

孙丹丹

(淮安市新马高级中学，江苏 淮安 211700)

本文对圆锥曲线参数方程在高中数学解题中的实际应用情况进行详细分析和研究，为学生学习成绩的提升打下良好的基础，提高学生的数学解题思路以及解题质量.

圆锥曲线参数方程、高中数学、解题、应用

数学本身就是一门比较复杂的学科，数学知识具有一定的抽象性和复杂性，学生学习起来比较困难，特别是对于高中生来说，更是如此.圆锥曲线方程是高中数学学习过程中非常重要的知识点之一，在高考当中占据的比重也比较大.在圆锥曲线定义当中，利用椭圆定义以及双曲线的具体定义，能够帮助学生更好地对数学问题进行解答.

一、利用圆锥曲线方程解决最值问题

传统数学学习方式主要是通过广泛的做题，对数学题型进行反复地训练，来达到强化学生记忆的目的，这样才能够保证学生自身的学习成绩能够不断提升.在实际教学过程中，针对学生学习能力以及学习进度问题，通过对一些典型习题的设计和应用，注重学生思维思考模式的培养，让学生能够养成举一反三的意识，这样不仅能够从根本上加强学生对于数学的感知能力，而且能够促使高中生的数学学习成绩有效提升.

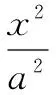
根据这道题目当中给出的条件，教师要引导学生在对这道问题进行解答的时候，不能够局限其自身的思维，要敢于想象.教师要引导学生将这道题目当中涉及的知识与其他知识之间进行有效的衔接，帮助学生找到解题思路.

解析根据题目可以设A(acosθ,bsinθ)，通过对四边形的观察，可以得到其四边与坐标轴分别保持平行状态，在这种条件下，可以推断四边形ABCD为矩形，其面积可以表示为S=4(acosθ×bsinθ)=2absin2θ.当S表示为最大值的时候，sin2θ是最大值，其值为1.当sin2θ=1的时候，S=2ab.四边形ABCD的周长可以表示为L=4(bsinθ+acosθ)=4(a2+b2)1/2sin(θ+β)，其中sinβ=a÷(a2+b2)1/2，cosβ=b÷(a2+b2)1/2.当sin(θ+β)为最大值1的时候，四边形的周长为最大.sin(θ+β)的值为1时，Lmax=4(a2+b2)1/2.

二、利用定义与正余弦定理求焦点三角形

在学生实际解题过程中，要培养学生发挥其自身的探索性思维，通过总结与小组合作的模式，从根本上提高学生的数学解题思维和能力.数学习题当中单一性的题目相对来说比较少，基本上都是与一些其他知识复合型的出现，难度系数也越来越高，这对学生的解题能力要求就比较高.

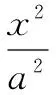
在本题中,根据基础知识，利用定义的深入了解和认识.通过正余弦定理，将面积公式与正余弦定理进行结合，能够得到准确的答案.

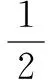
(1)

(2c)2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cosθ

(2)

通过与圆锥曲线中双曲线的定义能够得到

|PF1|-|PF2|=2a，

|PF1|2+|PF2|2-2|PF1|·|PF2|=4a2.

(3)

从而完成这道问题的解答.

三、圆锥曲线参数方程解题中应当注意的问题

在教学过程中，教师不仅要让学生能够深入地掌握一些理论性的知识或者是具体公式的用法，而且要让学生意识到如何将这些知识和公式与实践题目进行有效结合.在这种形势下，针对圆锥曲线参数方法方程的相关知识，教师要让学生多写、多练、多问、多记，让学生能够为日后的解题打下良好的基础.这样不仅能够帮助学生摸清题目的内涵，让学生在遇到数学问题时，能够了解其中所要表达的意思，完成快速有效的解题.

综上所述，高中数学在高中教育当中占据非常重要的地位，对学生高考也产生非常重要的影响.因此，在高中数学教学活动实施过程中，教师要注重对学生理论知识的强化，让学生能够将理论知识切实有效地应用到实践当中，这样不仅能够提高学生对于数学知识题目的理解力，而且能够锻炼学生举一反三的能力.通过对一些典型题目的讲解，能够促使学生解题思维以及解题质量的有效提升.

[1]毛芹.圆锥曲线参数方程在高中数学解题中的应用[J].理科考试研究：高中版，2014(21).

[2]陈荣明.直线参数方程教学设计[J].教学月刊：中学版，2011(23).

[3]李淑燕.用圆锥曲线的参数方程解题例谈[J].数理化学习：高三，2011(07).

G632

A

1008-0333(2017)22-0012-02

2017-06-01

孙丹丹(1985.1- )，女，吉林公主岭市人，中教一级，本科学历，从事高中数学教学.

责任编辑：杨惠民]