短期电力负荷时间序列预测的极限学习机方法

张宁

(闽江学院 物理学与电子信息工程系，福建 福州 350108)

短期电力负荷时间序列预测的极限学习机方法

张宁

(闽江学院 物理学与电子信息工程系，福建 福州 350108)

提出将一种进化的神经网络模型——极限学习机应用于短期电力负荷时间序列预测中，该方法具有模型参数设置少、训练速度快和良好的泛化能力等明显优点。通过实例分析表明该模型的预测精度要优于BP神经网络模型，同时也验证了该模型应用于短期负荷预测的有效性和可行性。

极限学习机;BP神经网络模型;短期电力负荷;时间序列

对短期电力负荷进行准确预测是电力系统安全稳定运行的重要前提。预测短期电力负荷经常根据气温、气压、相对湿度、降雨量、节假日等多种影响因素来进行建模。如果这些影响因素和电力负荷之间有良好的相关性，建立一定的数学模型可以获得较好的预测效果。但是，影响因素的取法众多，气温、气压、相对湿度等因素之间的组合也有多种形式，往往需根据经验来进行确定。为消除这些不确定组合方式的影响，另一种预测短期负荷的处理方法是将历史负荷值作为一时间序列进行建模分析。在此基础上，人们提出了灰色模型预报法、时间序列分析法、Kalman滤波法等[1-3]多种负荷预测方法，并取得了较好的应用效果。

随着机器学习理论的不断发展，以神经网络为代表的非线性方法在负荷预测中获得了较为成功的应用[4-5]。但神经网络方法存在参数设置较多、训练速度较慢、容易陷入局部极小等缺陷。为此，提出将极限学习机(extreme learning machine，ELM)模型应用于短期负荷预测中。该方法是由南洋理工大学Huang G B博士在2006年提出，为一种进化的神经网络方法，具有较好的泛化能力，并能避免传统神经网络方法存在的诸多问题[6]。应用该方法对实际负荷数据进行预测实验分析，结果验证了所提方法的可行性，并具有较高的预测精度。

1 极限学习机的基本原理

极限学习机是一种新型神经网络训练算法[7-9]，对于N个训练样本(xi,yi),i=1,2…,N，其中xi=[xi1,xi2,…,xin]T∈Rn为输入变量，yi=[yi1,yi2,…,yin]T∈Rm为输出变量，其ELM数学模型可以表示为：

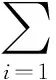
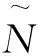
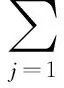
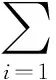
上式可表示成矩阵形式为：

其中：

H=

ELM模型的训练目标是寻找最优权值W=(w,b,β)，以使得下式成立：

ELM模型与传统BP神经网络模型的差异在于：BP神经网络模型采用梯度下降方法对W进行调整；而ELM模型是将(3)式作为一线性方程组进行求解，其输出权值β的最小二乘解为：

其中，H+为隐层输出矩阵H的Moore-Penrose广义逆[7]。则ELM模型的网络输出F为：

从上述原理可以看出，ELM模型具有训练误差最小、可得到权值的最小范式等显著的优越性。

2 基于ELM的短期电力负荷预测模型

2.1 样本数据集的构建

对于一实际短期负荷时间序列，我们假定t时刻的负荷值X(t)可以由(t-1,t-2,…,t-m)时刻的历史负荷值X(t-1),X(t-2),…,X(t-m)来进行预测，则预测模型可以表示成：

其中，f(·)为映射函数，m为嵌入维数。

由此，在选择一定的嵌入维数，即确定ELM网络输入个数的情况下，可以构造出一个多输入单输出的ELM模型。

2.2 短期负荷时间序列数据预处理

为了减少数据量纲对建模的影响，对原始短期负荷时间序列数据进行归一化处理，即使用下式将数据归一至[-1,1]：

其中，Xmin、Xmax为原序列中的最小值、最大值，X′(t)为经归一化后的负荷序列。在建模完成之后，对于输出的训练、预测数据，再进行反归一化处理，将其还原至原始区间。

2.3 模型的评价指标

3 实例分析

以国家电网浙江省台州某地区2010-02-14～2010-03-27共42d的电力负荷数据为研究对象。采集的数据为每天整点时刻的负荷值，共计1 008个，形成短期负荷时间序列。如图1所示。

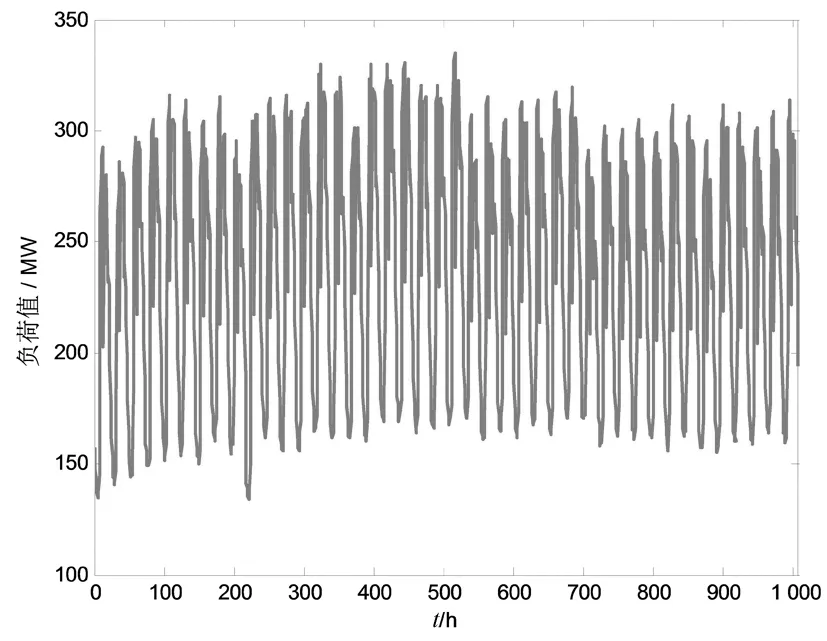
图1 原始短期负荷数据序列Fig.1 Original power load data series

对短期负荷时间序列构建样本集时，在采用不同嵌入维数的情况下，根据式(8)构建的样本数目是不相同的。为了方便数据间的对比，将嵌入维数分别设置为48、24、12，即由前两天、前一天、前半天的负荷数据预测下一整点时刻的负荷值。由此，总样本数目可构建为960、984、996个。

统一以最后一天24个负荷值为预测对象，则训练样本数目设置为936、960、972个，预测样本数目均为24个。以此为基础，建立ELM模型和常用的BP神经网络模型。其中BP模型采用稳健的Levenberg-Marquardt算法。由于两种模型原理的不同，ELM、BP的隐层神经元数对结果的影响也不同，一般ELM需设置较多的隐层神经元数。在本研究中，两种模型的隐层神经元数分别设置为30、8。激活函数统一选择为“Sig”函数。由于ELM和BP均采用随机权值，会使得模型预测单次结果出现不稳定现象，为此在进行预测时，各循环操作了50次，并取50次预测均值作为最终预测结果。

表1给出了不同嵌入维数下ELM模型、BP模型进行预测的精度统计及消耗的CPU时间。

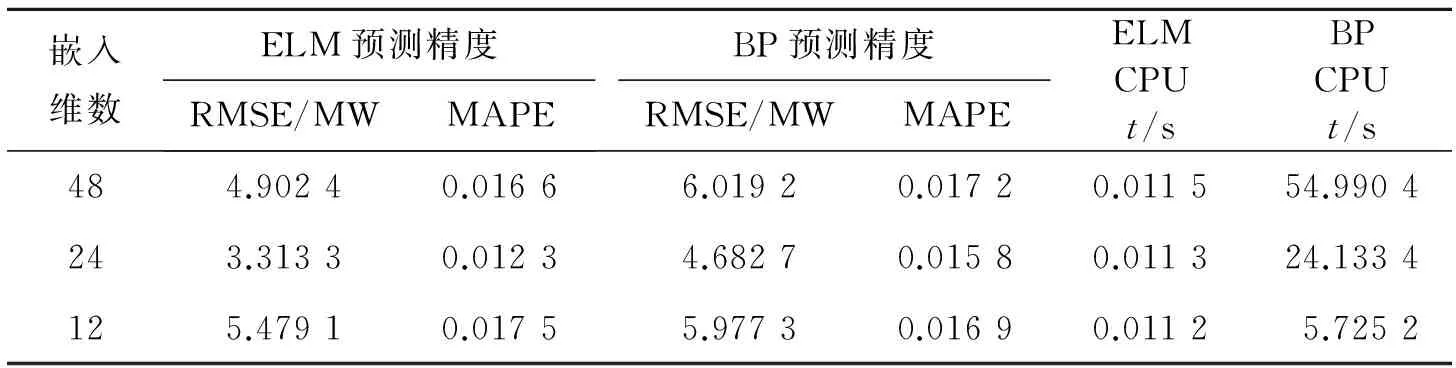
表1 两种模型平均预测精度和CPU时间Tab.1 Average predicted precision and CPU time for two models

从表1中可以看出：(1)在设置不同嵌入维数下，ELM模型的预测精度都要优于BP神经网模型，表明ELM模型具有良好的学习能力和泛化能力；(2)从CPU运行时间上对比，两种模型不在一个数量级上，ELM模型的运行速度要远快于BP神经网络模型，这是由于ELM直接解算线性方程组，而BP需要不断进行反向迭代运算造成的；(3)在嵌入维数取值为24，即以前一天的数据进行预测下一时刻负荷值时其预测精度最高。

以嵌入维数为24为例，预测最后一天24 h的负荷值，其预测值与实际负荷值的对比情况如图2所示，预测负荷的绝对误差如图3所示。

从图1中可以看出，所采用的ELM预测模型的预测结果曲线与真实负荷值曲线非常吻合。从图2中可以看出，ELM模型的预测绝对误差值分布在±5 MW范围之内，表明了ELM模型具有较高的预测精度。

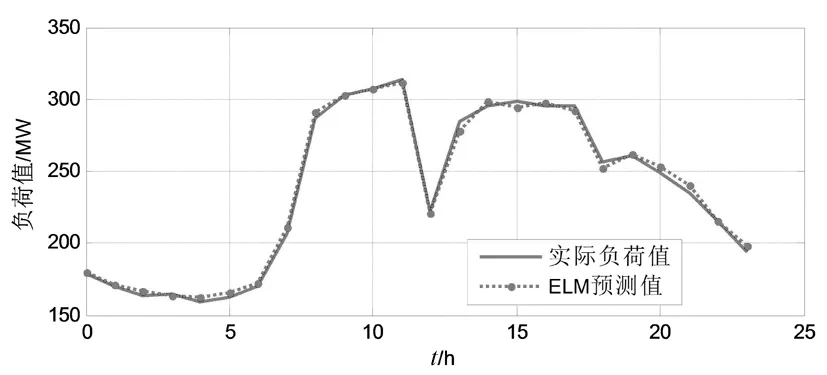
图2 实际负荷值与预测负荷值对比Fig.2 Comparison between practical load and predicted load

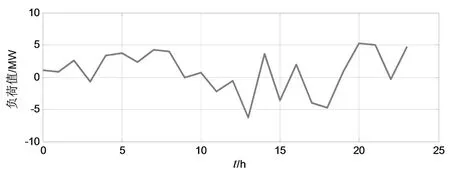
图3 负荷预测绝对误差Fig.3 Absolute error of load forecasting

4 结论

(1)将ELM模型应用于短期负荷时间序列预测中，取得了较高的预测精度，表明ELM模型在短期负荷预测中应用的可行性和有效性。

(2)本研究在对负荷时间序列进行样本构建时，其嵌入维数是根据经验来进行选取的，在实际中由于负荷时间序列具有混沌特性，可进一步通过相空间重构计算来选取最佳嵌入维数，这将在下一步的研究中予以实现。

(3)所采用的ELM模型预测精度虽较BP神经网络模型为高，但其本质仍然是一种基于经验风险最小化原则的进化神经网络，为此需利用结构风险最小化原则对其进行进一步改进，以提升其预测精度和泛化能力。

[1] 康重庆，夏清，刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007.

[2] 张思远，何光宇，梅生伟，等.基于相似时间序列检索的超短期负荷预测[J].电网技术，2008，32(12):56-59.

[3] 李明干，孙健利，刘沛.基于卡尔曼滤波的电力系统短期负荷预测[J].继电器，2004，32(4):9-12.

[4] 向峥嵘，王学平.基于小波-神经网络的电力系统短期负荷预测[J].系统仿真学报，2008，20(18):5018-5020.

[5] 李元诚 ，方廷健，于尔铿.短期负荷预测的支持向量机方法研究[J].中国电机工程学报，2003，23 (6) ：55-59.

[6] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine: theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[7] 邓万宇,郑庆华,陈琳.神经网络极速学习方法[J]．计算机学报，2010，33(2)：279-287．

(责任编辑：肖锡湘)

Extremelearningmachinemethodforshort-termpowerloadtimeseriesforecasting

Zhang Ning

(Physics &Electronic Information Engineering Department,Minjiang University,Fuzhou 350108,China)

The utilization of extreme learning machine—an evolution model of neural networks in short-term power load time series forecasting was proposed,which has the advantages of less parameter setting,fast training speed and better generalization ability.The validity and feasibility of the model were verified.The simulation results indicate that the forecasting accuracy of the model is better than that of BP neural network model.

extreme learning machine;BP neural network model;short-term power load;time series forecasting

TM715

A

1672-4348(2017)04-0367-04

10.3969/j.issn.1672-4348.2017.04.012

2017-07-20

福建省中青年教师教育科研项目(JAT170437)

张宁(1984-)，女，福建罗源人，讲师，硕士，研究方向：信号处理、智能优化算法。