最大灵敏度指标的分数阶内模控制器设计

那景童, 徐驰

(1.大连交通大学 电气信息学院,辽宁 大连 116028，2.北京化工大学 信息学院,北京 100029)

最大灵敏度指标的分数阶内模控制器设计

那景童1, 徐驰2

(1.大连交通大学 电气信息学院,辽宁 大连 116028，2.北京化工大学 信息学院,北京 100029)

针对分数阶控制器设计时参数整定复杂问题，提出一种基于最大灵敏度的分数阶内模控制器设计方法。首先采用粒子群优化算法对原系统模型进行简化处理，在模型简化基础上，根据内模控制原理设计分数阶内模控制器，该控制器仅有一个可调参数，通过这一可调参数可以实现所提控制器的快速整定。最后通过最大灵敏度指标实现分数阶内模控制器的鲁棒整定。仿真结果表明该方法具有良好的控制品质及克服参数摄动的鲁棒性。

分数阶控制；模型简化；内模控制；快速整定；最大灵敏度

0 引 言

分数阶PIαDβ控制器与传统PID控制器相比，多了两个可调参数(α,β)，当α=β=1时，控制器属于常规PID控制器，正是由于α，β连续可调，因此分数阶PIαDβ控制器具有更大的调节范围、更强的鲁棒性，为得到更优的系统动态性能创造了条件。但正是可调参数的增加增大了控制器参数的整定难度，文献[1]提出的基于控制系统期望带宽的IMC-PIαDβ控制器，但需要分析系统的频率响应特性；在其中设计的IMC-PIαDβ控制器，通过引入内模控制准则减少了分数阶控制器的整定参数，但该方法设计过程中未考虑控制模型参数变化的情况，当系统工作环境发生变化时，所设计的控制器性能会急剧下降。

针对上述问题，本文采用粒子群优化算法对原被控模型进行简化，在简化模型的基础上将内模控制思想引入到分数阶控制器设计中，利用内模控制原理有效减少分数阶控制器参数的整定，并基于最大灵敏度指标实现了控制器的鲁棒整定。

1 系统模型简化和分数阶内模控制器设计

1.1 系统模型简化

文献[2]针对分数阶微分算子，采用改进的Oustaloup滤波器进行有理传递函数逼近，得到高阶整数阶模型，这样导致系统控制器的设计变得更加复杂。所以针对分数阶系统进行模型简化是很有必要的，在模型简化过程中大部分分数阶模型都可以用如下式(1)模型结构进行逼近：

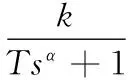
(1)

粒子群优化(PSO)算具有较强的全局搜索能力和鲁棒性且不需要目标函数的特征信息，因此本文采用该优化算法进行算法[3]模型简化处理。对于粒子群优化算法重点，目标函数的选取，本文所选目标函数为原系统模型和简化模型的单位阶跃响应误差，即:

(2)

式中n为搜索次数，y(t)和ym(t)分别为原系统模型和简化模型的单位阶跃响应。

1.2 分数阶内模控制器设计

内模控制是将实际对象与对象模型相并联，控制器取模型的动态逆，从而满足闭环系统性能，并通过添加低通滤波器来增强系统的鲁棒性。内模控制的结构如图1所示，其中R(s)、Y(s)、D(s)分别为设定值、系统输出和外来扰动,Gp(s)和GFo(s)分别为实际被控对象模型和简化模型。

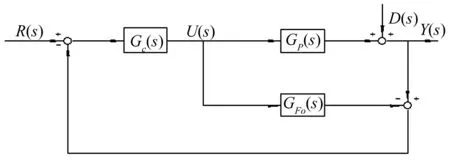
图1 内模控制框图

在传统反馈控制中，反馈控制器C(s)可通过内模结构中Gc(s)与GFo(s)结合而成:

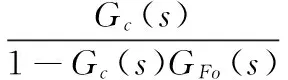
(3)

分数阶内模控制器设计与内模控制类似，主要分为如下两步：

1)模型分解：

(4)

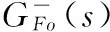
2)根据内模控制原理可得内模控制器Gc(s)可表示为：

(5)

式中f(s)为低通滤波器，其通常形式可表示为：

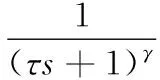
(6)

这里γ是为了保证系统的物理可实现，τ为滤波器f(s)参数，也是内模控制中唯一可调参数，减小τ系统动态性能得到提高但鲁棒性变差，增大τ情况正好相反。

2 基于最大灵敏度的分数阶内模控制器参数整定

过程控制中，用于控制器设计的系统模型一般都不够精确。因此，控制器的设计应考虑对参数变化的鲁棒性[4]。基于上述所提问题考虑，本文利用最大灵敏度Ms来设计FOIMC控制器。最大灵敏度定义如式(7)所示：

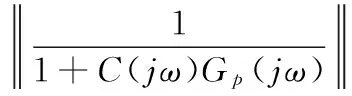
(7)

式中C(jω)Gp(jω)为系统开环传递函数，最大灵敏度是指系统开环传递函数的Nyquist曲线与临界(-1,0)的最短距离的倒数。

文献[5]指出，Ms的取值范围为1.1～2.5之间且Ms越小系统的鲁棒性越强。若：

Gl(jω)=C(jω)Gp(jω)

(8)

则有：

(9)

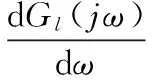
(10)

其中θ为过临界点与C点的直线与负实轴的夹角。若GFo(s)=Gp(s)，由式(3)可得系统的开环传递函数为：

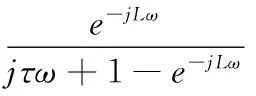
(11)

令

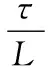
(12)

将式(12)代入到式(11)可得：

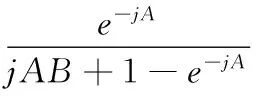
(13)

将式(13)代入到式(9)(10)，利用Matlab中fsolve函数求解可得到B与Ms的表达式：

(14)

由式(14)可得滤波器参数τ与Ms的关系式：

(15)

其中L为已知常数，由给定的Ms和式(15)可以得到滤波器f(s)的时间常数τ。

3 仿真及结果分析

考虑分数阶被控对象[6-7]：

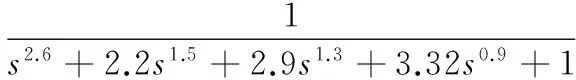
(16)

利用本文1.1节所提PSO优化算法对式(16)进行模型简化，优化结果为：

θ=[K,T,α,L]=
[0.994 6,6.230 1,1.039 4,0.299 6]

(17)

因此，可得式(16)的化简模型为：

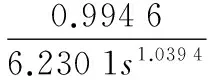
(18)

针对简化模型式(18)设计分数阶内模控制器，这里取Ms=1.2，由本文第二节控制器设计步骤可得分数阶内模控制器为：

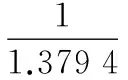
(19)

文献[6]针对式(18)给出了最优分数阶PID控制器为：

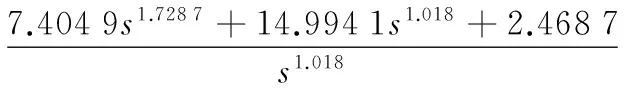
(20)

文献[7]针对式(16)给出的一种分数阶内模PID控制器为：

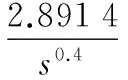
(21)

分别采用本文方法，文献[6-7]方法得到系统的单位阶跃响应如图2所示。

图2 系统单位阶跃响应对比

从图2可得，本文设计的分数阶内模控制器相比文献[6-7]所提控制器具有上升时间短、稳态误差小、存在微小超调，综合考虑本文所提分数阶内模控制器具有良好的控制品质。

4 结束语

本文针对以往分数阶控制器参数整定复杂问题，提出一种基于最大灵敏度的分数阶内模控制器设计方案。利用PSO算法对原系统模型进行简化处理，然后将内模控制思想引入到简化模型中设计分数阶内模控制器，所得控制器仅有一个可调参数，再通过灵敏度指标Ms推导出控制器唯一参数的数学表达式。仿真结果可说明文章所提方法是行之有效的。

[1] LI D Z, FAN W F, JIN Q B, et al. An IMC-PIλDμcontroller design for fractional calculus system[C].Proc of the 29th Chinese Control Conf. Beijing: IEEE, 2010:3581-3585.

[2] 薛定宇. 控制数学问题的MATLAB求解[M]. 北京: 清华大学出版社，2007．

[3] BIRGE B. 2003,PSOt, A particle swarm optimization toolbox for matlab[J]. IEEE Swarm Intelligence Symposium Proceedings, 2003(4):24-26.

[4] KAYA I. Two-degree-of-freedom IMC structure and controller design for integrating processes based on gain and phase-margin specifications[C]. IEE Proc of Control Theory and Applications. IET, 2004, 151(4): 481-487.

[5] JIN Q B, LIU Q, WANG Q, et al. PID controller design based on the time domain information of robust imc controller using maximum sensitivity[J]. Chinese J of Chemical Engineering, 2013, 21(5): 529-536.

[6] DAS S, PAN I, DAS S, et al. Improved model reduction and tuning of fractional-order PIλDμcontrollers foranalyticalrule extraction with genetic programming[J]. ISA Trans, 2012, 51(2): 237-261.

[7] 李大字，刘展，曹娇． 基于IMC方法的分数阶系统控制器设计[C]//2007 仪表自动化及先进集成技术大会论文集． 北京: 仪器仪表学报杂志社，2007.

Design of A Fractional Order Internal Model Controller with Maximum Sensitivity Index

Na Jingtong1， Xu Chi2

(1. College of Electrical Information, Dalian Jiaotong University, Dalian Liaoning 116028, China;2. School of Information, Beijing University of Chemical Technology, Beijing 100029, China)

With respect to complicated parameter setting in the design of fractional order controllers, this paper proposes a scheme for designing fractional order internal model controller based on maximum sensitivity. Firstly, the original system model is simplified through particle swam optimization (PSO) algorithm. Based on the simplified model, a fractional order internal model controller is designed in the principle of the internal model control (IMC). The proposed controller has only one adjustable parameter，through which its rapid setting can be realized. Finally, robust setting of the fractional order internal model controller is realized through the maximum sensitivity index. Simulation results show that this approach has good control quality and robustness to overcome parameter perturbation.

fractional order control； model simplification；internal model control；rapid setting；maximum sensitivity

10.3969/j.issn.1000-3886.2017.04.005

TP202.3

A

1000-3886(2017)04-0015-03

定稿日期: 2016-12-19

那景童(1989-)，男，辽宁大连人，大连交通大学硕士生。 徐驰(1990-)，男，江苏淮安人，北京化工大学博士生。