永磁同步电机变频调速系统的内模控制

李明辉

(西继迅达电梯有限公司,河南 许昌 461000)

永磁同步电机变频调速系统的内模控制

李明辉

(西继迅达电梯有限公司,河南 许昌 461000)

永磁同步电机是典型的非线性多变量强耦合系统，在同步旋转坐标系下dq轴电流存在耦合，传统的PI控制器无法实现解耦，提出一种基于内模控制原理和空间矢量算法相结合的高性能永磁同步电机解耦控制方法，用内模控制策略控制理想电机模型，对定子电流交叉耦合电势动态解耦，提高系统的动态响应性能，同时在整个电流闭环过程中对参数摄动和外扰动具有良好的鲁棒性，这种方法不需要额外的电机参数和检测硬件，实验结果验证了方法有效可行。

永磁同步电机；内模控制；解耦；稳态误差;观测器；空间矢量脉宽调制

0 引 言

永磁同步电机以其体积小、功率密度高、转矩/惯量比高等特点在电梯行业应用非常广泛，低速大转矩的应用特性决定了电梯永磁同步曳引机多采用凸极效应明显的外转子集中绕组结构，集中绕组永磁同步电机含有丰富的定子磁势谐波，在同步旋转坐标系下定子电压中耦合电压和反电势对dq轴电流交叉耦合作用复杂[1]。传统同步PI控制依赖电机本体参数，且忽略了dq轴电流交叉耦合，实际工程中，当其中一个轴上的电流改变时，对另一轴上电流产生瞬时误差，使转矩输出产生瞬时畸变，影响系统动态性能。

内模控制作为一种先进的控制技术，它不过分依赖于被控对象的准确数学模型，在PI解耦电流主控器的基础上，构造电流环的内模状态方程，利用IMC原理设计电流环观测器，实现电流补偿控制，对系统内部参数摄动及外部环境扰动具有自适应性，系统跟踪性能好，鲁棒性强 ，控制器参数单一，结构和算法简单，调整方向明确，工程上易于实现[2]。

1 PMSM的数学模型

不考虑永磁同步曳引机的制动系统，永磁同步曳引机(PMSTM)可简化为凸极效应明显的永磁同步电机(PMSM)，在同步旋转坐标系下数学模型为：

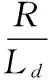
(1)

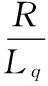
(2)

式中Ld、Lq分别为直轴和交轴电感；ψ为转子磁钢产生的永磁磁链；R为定子绕组电阻；ω为转子电角速度；id、iq分别为直轴和交轴电流；ud、uq分别为直轴和交轴电压。

由式(1)和式(2)可见模型的准确度依赖于系统参数[3]。对定子电流id、iq表现为一阶时间滞后环节，d轴和q轴电流分别对q轴和d轴方向产生耦合电动势。如果定子电流id、iq完全解耦，由式(1)和式(2)可得式(3)和式(4)：

ud0=ud+ωLqiq=Rid+Ldid

(3)

uq0=uq-ωLdid-ωψ=Riq+Lqiq

(4)

式中ud0、uq0分别为电流解耦后的直轴和交轴电压。

2 基于IMC观测器的PMSTM控制设计

内模控制的原理是利用反馈滤波器来改善鲁棒性和对抗性，本质是一种鲁棒控制方法，是PI控制的扩展，等效于交叉解耦的PI控制[4]。其原理如图1所示，图中：R(s)为参考输入，F(s)为信号反馈，E(s)为PI控制器输出，C(s)为内模控制器，G(s)为系统传递函数，Gm(s)为内模，d(s)为扰动信号，Y(s)为输出。

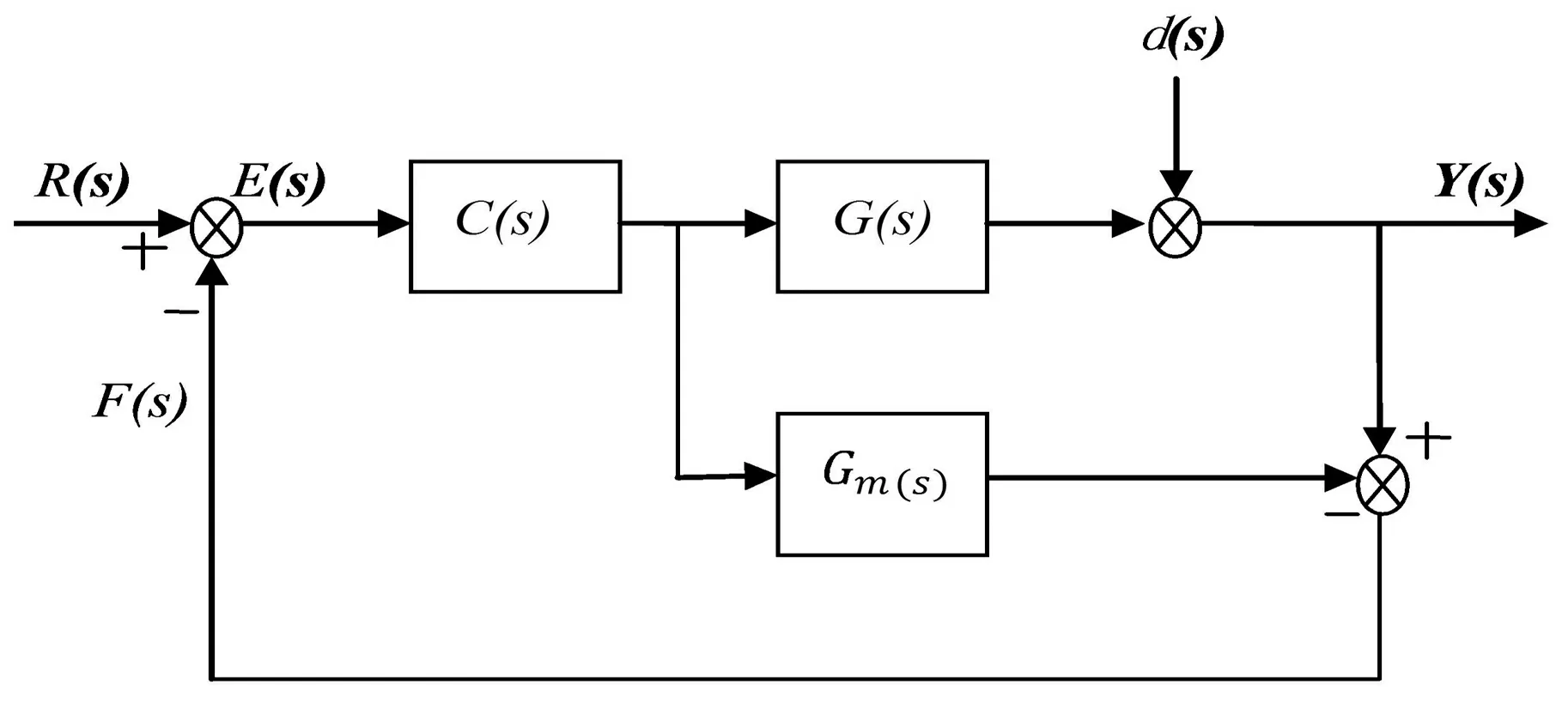
图1 内模控制原理图

根据图1得：

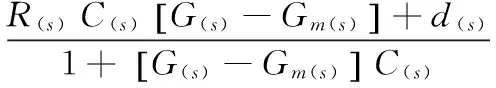
(5)

Y(s)=[R(s)-F(s)]G(s)C(s)+d(s)

(6)

如果内模建模精确，与系统模型匹配，即Gm(s)=G(s)，则由式(5)、式(6)得：

F(s)=d(s)

(7)

Y(s)=R(s)G(s)C(s)+d(s)[1-G(s)C(s)]

(8)

由式(7)可知，系统反馈信号F(s)就是扰动信号d(s)，由式(8)可知，如果C(s)G(s)=1，C(s)=1/G(s)，系统可对扰动信号进行完全补偿，Y(s)=R(s),系统实现开环系统控制，输出信号可以直接跟踪输入信号[5]。

按照上述内模控制原理，将式(3)和式(4)拉普拉斯变换后得：

Uq_f(s)=RsIq(s)+sLqIq(s)+ωrLdId(s)

(9)

Ud(s)=RsId(s)+sLdId(s)-ωrLqIq(s)

(10)

令：

可得I(s)=D(S)U(s)

(11)

其中

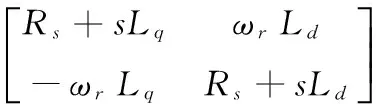
若使C(s)=D-1(s)，就构成内模控制，使得输出Y(s)=R(s)，则输出电流可以直接跟踪指令电流，由于D(s)表现为一阶系统，没有纯时延和右半平面的零点，系统是天然稳定的，为了优化控制器参数，增加一个低通滤波器，增强系统鲁棒性，定义：

C(S)=D-1(s)L(S)

(12)

式中

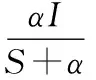
(13)

将内模结构模型等效为反馈控制模型，如图2所示。

其中

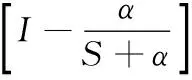
(14)

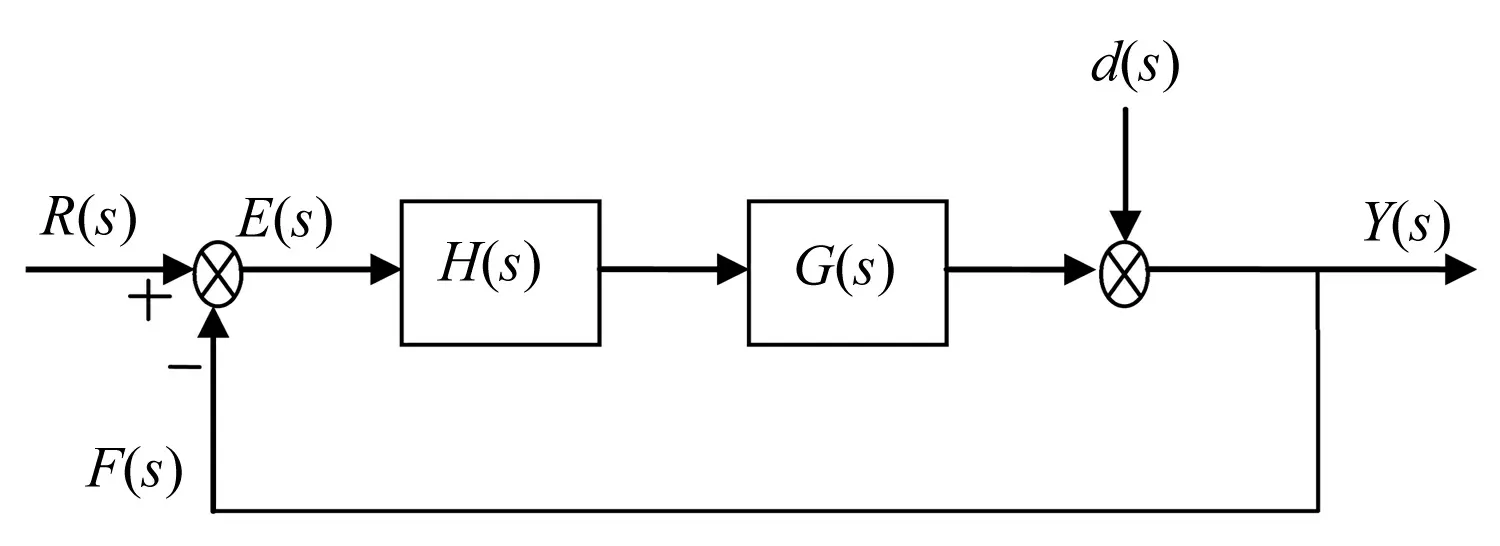
图2 等效反馈控制模型

可以看出内模控制本质是PI控制的一个扩展，等效于交叉解耦的PI控制[6]。从以上分析可以得到如图3所示的电流内模解耦控制器框图。

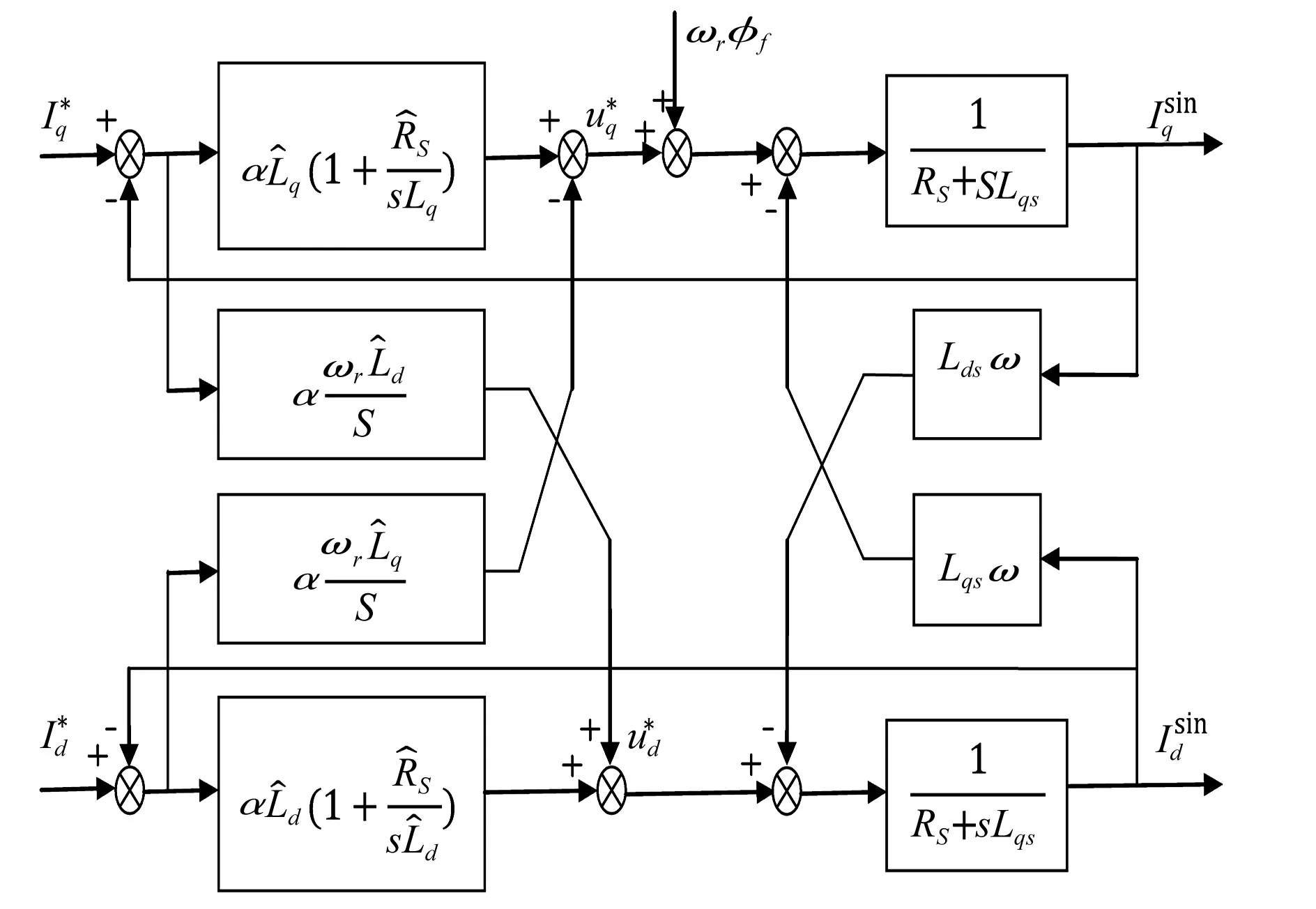
图3 电流内模解耦控制器

由图3可知，内模解耦控制调节参数只有α，算法简单，参数单一，在线调试方便，且系统没有超调，是天然稳定的，系统阶跃响应上升时间与参数α的关系为：

(15)

由式(15)可知，系统响应时间tr与调节参数α成反比例，增大调节参数α将减小系统响应时间，加快系统响应速度，但是α不能无限增大，实际工程中系统响应时间受限于硬件的电气时间常数[7]。

3 内模控制在SVPWM电流环控制中的应用

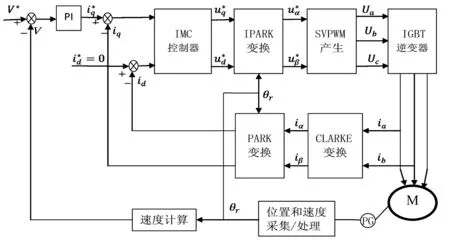
图4 带内模控制器的SVPWM控制系统图

4 实验平台的硬件和软件设计

4.1 硬件设计

实验平台硬件组成框图如图5所示：采用美国TI公司的TMS320F2812 DSP最小系统为核心算法处理器，德国SEMIKRON的SKD75为三相整流电路，日本三菱公司的PM75RLA120 IPM为三相电压源逆变器，以瑞士LA霍尔电量传感器和德国海德汉公司ERN1387 sin/cos编码器为反馈传感器，组成永磁同步电机变频调速驱动控制平台，霍尔电流传感器将A，B相电流隔离转换成电压信号，经过运放电路输入到DSP的A/D模块进行采样计算、内模控制器交叉解耦等处理得到反馈电流分量，与sin/cos编码器C、D采集的转子角度位置信息一起参与电流环的调节运算，sin/cos编码器A、B经过比较电路获取正交信号,输入到DSP的正交编码脉冲电路(QEP),通过检测脉冲的边沿信号4倍频后给DSP内部计数器，计算出转子反馈速度,参与速度环的调节运算。

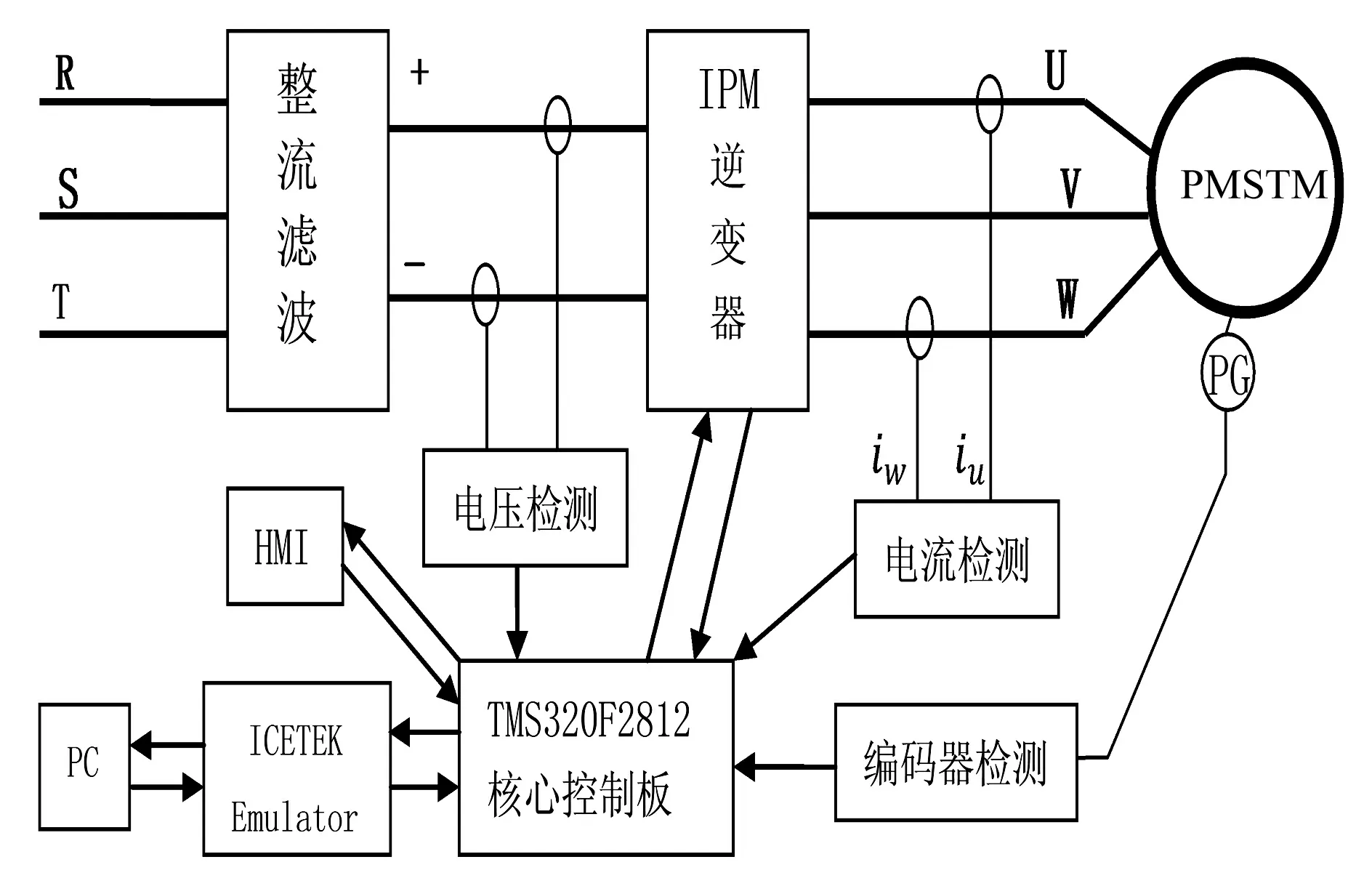
图5 实验系统组成框图

4.2 软件设计

系统软件设计主要有主程序、中断程序和子程序三部分组成。主程序主要完成DSP内部控制寄存器的初始化，系统上电自检，函数初始化，参数的设定、标幺，中断处理，HMI调用等，如图6(a)所示。考虑到永磁同步电机控制的实时性和快速响应，把电流、电压、编码器的信号采集，控制算法以及SVPWM波的产生，功率器件保护等放在定时中断程序里，如图6(b)所示。将通讯、人机交互、算法单元等编译成子程序供调用。

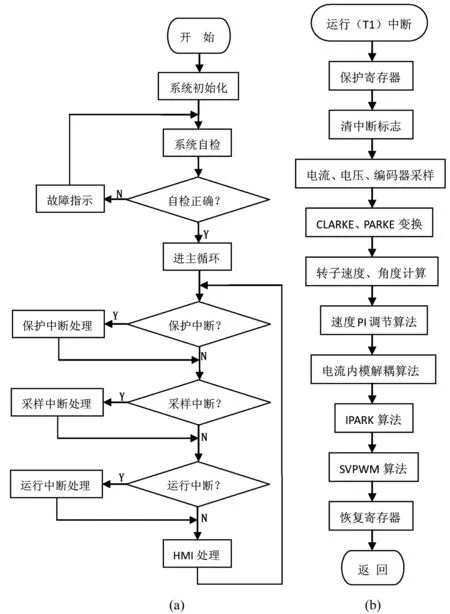
图6 电机控制程序流程图

内模控制软件实现例程如下：

Interrupt void MainISR(void)

{

. . .

EvaRegs.EVAIMRA.bit.T1UFINT =0;

ReadAdc(&adcdata);

ChangeAdc(&adcdata);

Clarke.calc(&clarke);

Park.calc(&park);

PID_spd.calc(&pid_spd);

ObserveAng.calc(&ObserveAng);

IMC_idq.calc(&imc_idq);

Ipark.calc(&ipark);

Svgen_dq.calc(&svgen_dq);

PWM.update(&pwm);

. . .

}

5 实验及结果分析

实验平台中选用的永磁同步电机额定转速为180 r/min，额定功率11.7 kW,额定电流24 A,额定转矩670 N·m，磁极数24极，定子相电阻0.345 Ω，电感14.2 mH,电流环采样频率选取16 kHz，速度环采样频率选取160 Hz，采用内模交叉解耦控制和PI控制对比，每个采样周期在TMS320F2812的缓冲区中记录速度、电流的指令值和反馈值，利用DLOG4CH四通道软件记录模块，通过XDS510仿真器将记录数据发送到CCS仿真软件，利用软件的Graph功能实时记录、比较指令值和反馈值之间的误差。通过HMI的SCI串行通信接口将采样数据传送到PC中，运用Matlab进行存储、处理分析、比较显示。

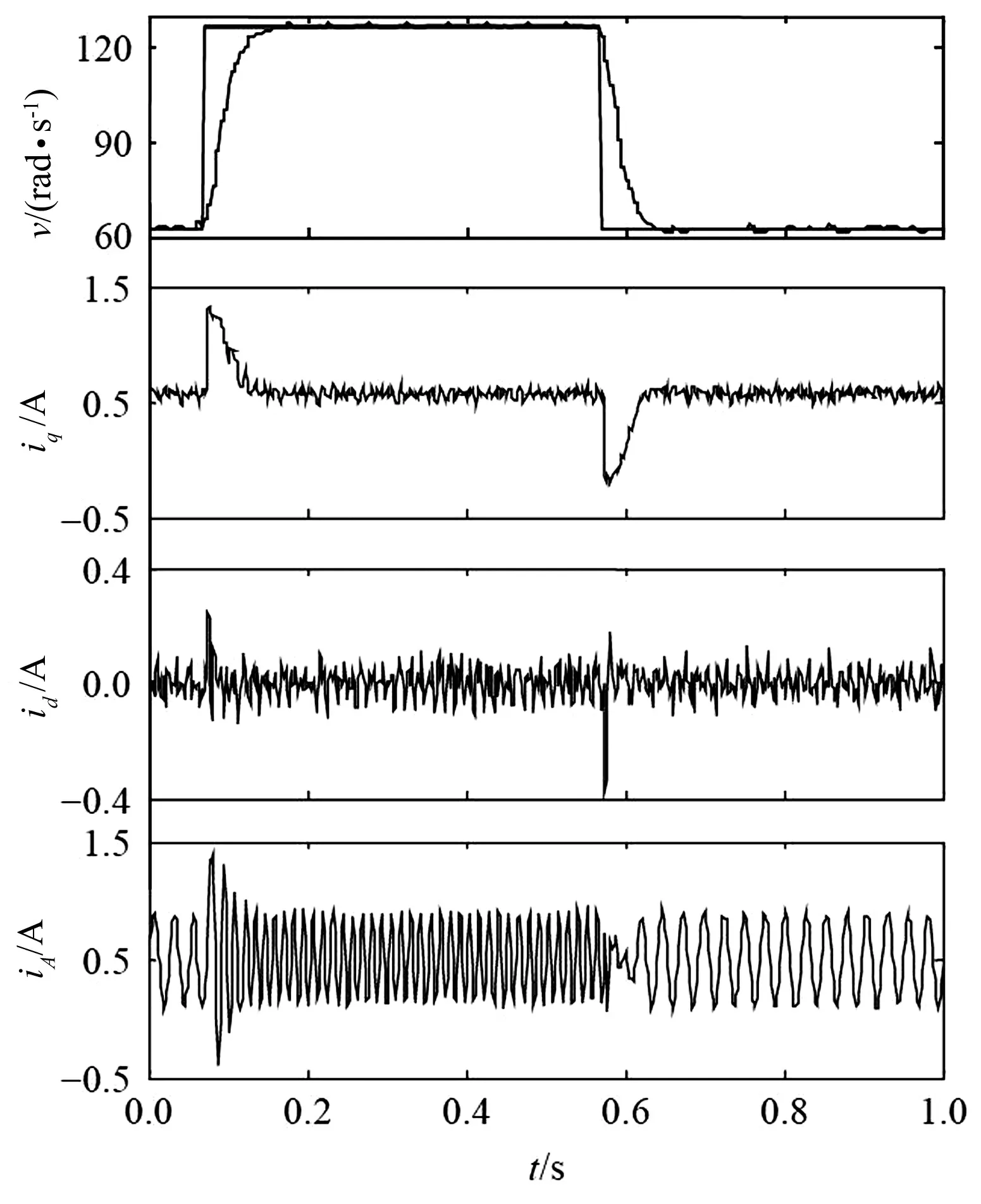
图7 IMC控制得到的ω、iq、id和iA

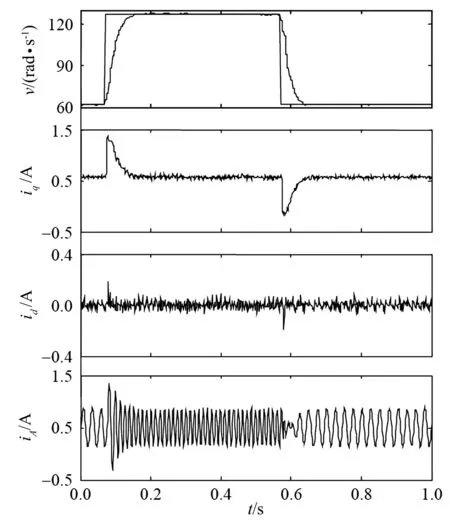
图8 PI控制得到的ω、iq、id和iA

实验中，初始角速度给定为20π rad/s,在t=0.08 s时刻角速度给定由 20π rad/s升为40π rad/s, 在t=0.57 s时刻角速度给定从40π rad/s降到20π rad/s，每间隔6.25 ms获取一组PMSTM角速度ω、电流iq、电流id、A相电流iA实验数据，将实验数据绘制成图7、图8的时域曲线，

图7和图8分别为IMC交叉解耦控制和传统PI控制所得到的角速度ω、电流iq、电流id、A相电流iA的时域曲线图，两种控制方式所得到的角速度ω的响应时间基本相同，IMC控制所得到的角速度ω的稳态误差为PI控制的40%，iq和id电流纹波值为PI控制的50%，对电流环实现更好的补偿控制。

通过对角速度ω分别为10π rad/s、20π rad/s、30π rad/s、40π rad/s、50π rad/s时，IMC和PI控制方式实验所得数据统计分析，得出如表1两种控制方式的主要参数对比，可见，在IMC控制方式下的角速度稳态误差小于PI控制方式下的角速度稳态误差，而且，随着角速度越大稳态误差越小；IMC控制方式下的iq和id电流纹波值小于PI控制方式下的iq和id电流纹波值，而且，随着角速度越大电流纹波值越小。

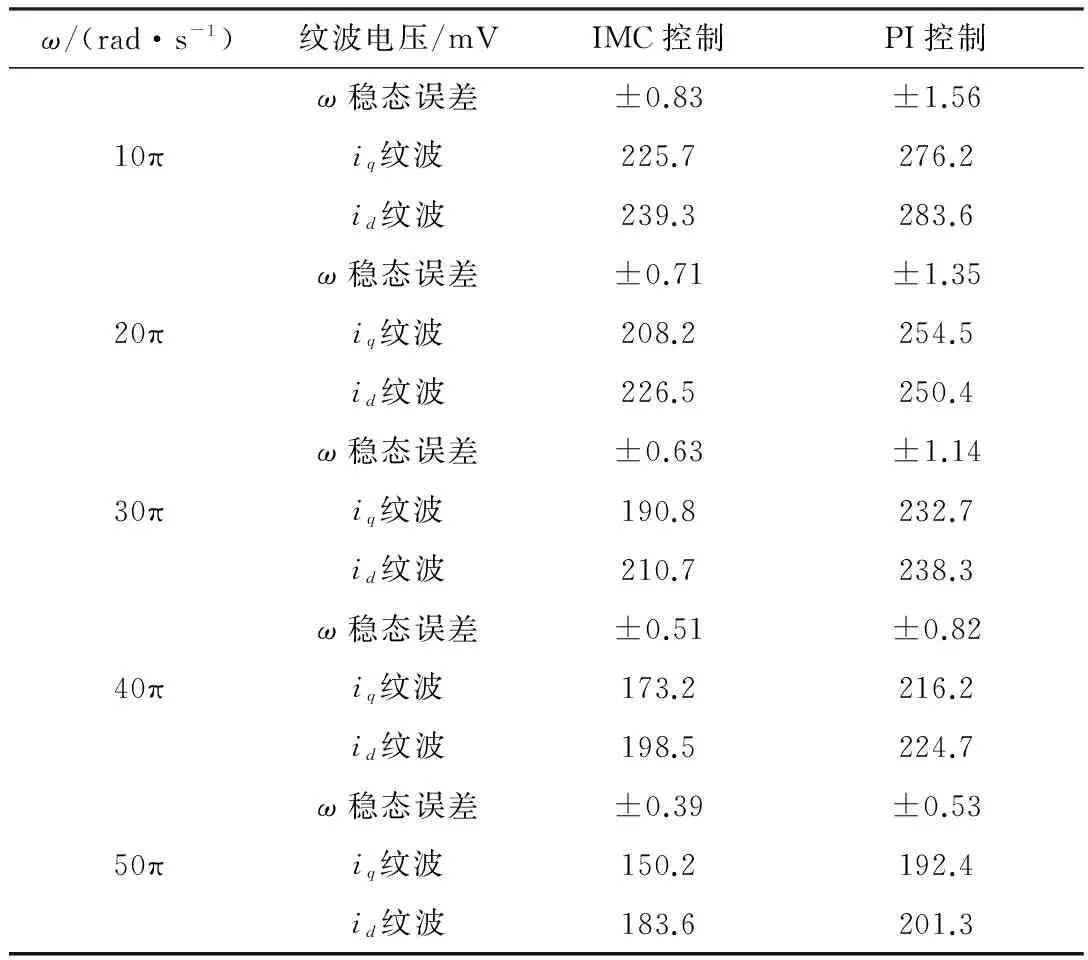
表1 IMC和PI控制方式的实验结果

6 结束语

本文针对电梯永磁同步电机多变量强耦合系统，受参数摄动和外扰动影响问题，利用IMC原理，构造电压和电流的内模方程，提出一种基于内模控制原理和空间矢量算法相结合的交叉解耦控制方法，系统响应快，鲁棒性好，在动态和稳态下都能达到很高的控制精度，控制算法易于用DSP实现，适用于转子磁场定向的SVPWM矢量控制，经过基于TMS320F2812实验平台的工程实际验证，各项指标满足电梯永磁同步电机控制要求。

[1] 郭新华,温旭辉，赵峰，等.基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J]. 中国电机工程学报, 2010,30(27):7-13.

[2] 葛宝明.永磁同步电机磁阻转矩的有效利用及其预测控制系统[J].电工技术学报，2000,15(3):6 -10.

[3] HARNEFERS L，NEE H P.Model-based current control of AC machines using the internal model control method[J].IEEE Trans.IA，1998,34(1):133-141.

[4] 陈志辉.IMC控制在双凸极发电机电压调节中的应用[J].电工技术, 2000,21(6):28-29.

[5] KARABACAK MURAT，ESKIKURT H IBRAHIM．Speed and current regulation of a permanent magnet synchronous motor via nonlinear and adaptive backstepping control[J]．Mathematical and Computer Modeling，2011，53(9)：2015-2030.

[6] 刘颖，周波，方斯琛．基于新型扰动观测器的永磁同步电机滑模控制[J]．中国电机工程学报，2010，30(9)：80-85．

[7] YASSER A R I M，EHAB F E S．A current control scheme with an adaptive internal model for torque ripple minimization and robust current regulation in PMSM drive systems[J]． IEEE Transactions on Energy Conversion，2008，23(1)：92-100．

[8] 王伟华，肖曦．永磁同步电机高动态响应电流控制方法研究[J]．中国电机工程学报，2013，33(21)：117-123．

IMC of Variable-frequency Speed Control System of Permanent Magnet Synchronous Motors

Li Minghui

(XJ Schindler Elevator Co., Ltd., Xuchang Henan 461000, China)

The permanent magnet synchronous motor is a typical nonlinear multi-variable system with strong coupling. There is coupling with dq shaft current in the synchronous rotating reference frame, and the traditional PI controller cannot realize decoupling. This paper proposes a high-performance permanent magnet synchronous motor decoupling method combining internal mode control (IMC) and space vector algorithm. IMC strategy is used to control an ideal motor model to realize dynamic decoupling of the cross-coupling potential of the stator current to improve dynamic response of the system. In the meantime, this approach shows good robustness toward parameter perturbation and external disturbance in the whole process of current closed loop, and there is no need for additional motor parameter or test hardware. Experimental results verify that this approach is effective and feasible.

permanent magnet synchronous motor; internal model control (IMC); decoupling. steady-state error; observer; space vector pulse width modulation

10.3969/j.issn.1000-3886.2017.04.004

TM341

A

1000-3886(2017)04-0011-04

定稿日期: 2016-11-08

国家质检总局公益性行业科研专项资助项目(G2013709);河南省博士后研发基地资助项目 豫人社博管[2015]8号

李明辉(1970-)，男，河南许昌人，本科，高级工程师，从事电梯驱动与控制研究。