基于TB-PC算法的MISO系统辨识的研究

耿健， 张雨飞， 范赫

(东南大学 能源与环境学院，江苏 南京 210096)

基于TB-PC算法的MISO系统辨识的研究

耿健， 张雨飞， 范赫

(东南大学 能源与环境学院，江苏 南京 210096)

如何保持MISO系统辨识的精确度、收敛度、耗时以及跳出局部最优解，是当今研究的热点和难点。提出了一种基于协同进化策略和禁忌搜索的蝙蝠和粒子群混合算法(TB-PC)，分析蝙蝠算法控制参数，提出了合理的脉冲频度和音强初值，将蝙蝠算法与粒子群算法的优势用协同进化结合起来，并引入了禁忌搜索。通过对四个测试函数和MISO系统实例的辨识仿真，验证了TB-PC算法具有稳定性能好、收敛精度高等优点，对MISO系统有优良的辨识效果。

TB-PC算法；MISO系统辨识；BA算法；POS算法；协同进化；禁忌搜索

0 引 言

在现实应用中，很多的实际过程和应用系统，比如热工过程，生物化学反应过程以及微型燃气轮机冷热电联供系统(MGT-CCHP系统)等都存在着时间延迟。所以，进行这些系统、过程辨识建模，对控制、预测、综合和分析具有重要的意义[1]。辨识带有时间延迟的系统，现阶段主流的辨识方法有两种，一种是使用有理传递函数法来进行逼近时间延迟；但是此方法需要用到大量的估计参数，对于具有很大时间延迟的系统过程来说，会带来很大的误差，偏离实际系统。另一种方法是采用非线性优化法，利用梯度逐级递推来搜索得到最优解；但是搜索得到最优解常常会收敛于局部最优解，不能得到全局最优解[2]。

对于未知时间延迟多输入单输出( MISO) 系统来说，非线性优化法方法更容易收敛到局部最优值。并且，如何保持辨识模型的精确度、收敛度以及所耗时长，都是需要解决的问题，是当今研究的热点和难点。本文的研究对象，即为含有多个未知时间延迟的MISO系统。首先，介绍了基本蝙蝠算法，其理论基础易于理解。接着，提出了一种基于协同进化策略和禁忌搜索的蝙蝠和粒子群混合算法(bat algorithm cooperative with particle swarm optimization based on tabu search strategy，TB-PC)，改进了蝙蝠算法难以跳出局部最优值、收敛速度不高、准确度低的缺点。然后，对TB-PC算法做了性能测试，其具有全局寻优搜索性能好、稳定性能好和收敛精度高等优点。最后利用仿真实验，验证这种算法对MISO系统辨识显著有效性以及准确性。

1 蝙蝠算法基本原理

蝙蝠算法(bat algorithm ,BA)是将自己追捕猎物的动作模仿为智能体随机分布在搜索空间范围内，衡量个体与猎物空间距离采用的是目标函数；蝙蝠自身搜索目标和移动滑行行动作模拟成用更加接近目标简单迅速动作来代替寻优过程可行解[3]。此时，对蝙蝠的回声定位系统提出以下假设，用来模拟其追捕猎物的过程[4-5]：

(1) 感应蝙蝠个体与猎物之间的距离，用的是自身的回声定位；并且其能够准确的区分出猎物与其他障碍物之间的区别。

(2) 蝙蝠在固有位置xi上是利用速度vi任意飞行，音强A0、可改变波长λ和频率f大小值去寻找猎物的；并且其可以利用猎物以及蝙蝠个体之间距离差大小来改变波长，在离猎物很近时及时改变蝙蝠个体发出波频度r∈[0,1]。

(3) 音强A从最大值(正值)A0减小到固定最小值Amin。

蝙蝠算法中并没有采取光线追踪来预算空间规模以及时间延迟大小，这就大大减少了多维问题的计算量。由于波长λ和频率f符合v=λf规律，即在特定的频率内[fmin,fmax]必与特定波长[λmin,λmax]相一致，波长λ这个量就可以舍弃。但是在特定波长λ，通过调整其频率f的大小来完成寻找目标，所以蝙蝠个体的飞行行为跟音强Ai以及频度ri相关。如果Amin=0，就是蝙蝠个体马上发现目标之后，没进行其他行动，音强Ai以及频度ri迭代式如式(1)、式(2)所示。

(1)

(2)

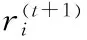
(3)

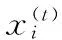
(4)

式中ε∈[-1,1]是一个任意的数字；xbest是当前全局最优位置。

fi=fmin+(fmax-fmin)×rand

(5)

(6)

(7)

式中fi∈[fmin,fmax]为蝙蝠个体i寻找目标所采取的频率值，其掌握着粒子移动节拍与界限。

2 蝙蝠算法的改进

蝙蝠算法有着参数较少、很简单就能够实现以及操作简单方便等优点，但也存在着求解精度偏低、收敛速度慢与难以跳出局部最优等缺点[6]。针对蝙蝠算法上述不足之处，本文一种提出基于协同进化策略和禁忌搜索的蝙蝠和粒子群混合算法(bat algorithm cooperative with particle swarm optimization based on tabu search strategy，TB-PC)，鉴于禁忌策略能够实现算法逃离局部最优解，进而避免陷入到其中去，提高群体多样性；同时结合粒子群算法，对算法搜索机制稳定性能够加以保障，提高系统辨识收敛精确度。

2.1 BA与PSO协同进化

协同进化是一种模仿自然界生态系统中物种间的协作进化机制而得到的策略，它借鉴了生态学的种群协同理论，运用了种群间的自动调节、自动适应原理。协同进化的各个种群相互驱使，相互影响和制约，以提高各自和全局的性能。基本的BA算法为了得到全局最优解，使运行速度得到提高并且降低xbest陷入到局部最优的机率，会跟着脉冲频度ri和音强Ai的进化；但是种群的多样性没有被有效的保护，比如当xbest是局部最优值时，就会提前收敛，从而群体空间的多样性就消失了。基本的PSO算法，不须要大量的梯度信息，收敛精度高以及参数较少，便于实现；但是其寻优所花费时间较长，算法运行到中后期时极其容易陷入到局部最优中去。综上两种算法，各有各的寻优优势，寻优的原理不尽相同，但是都存在着较容易陷入到局部最优中的缺点[7]。

TB-PC算法综合了两种算法的优点，以协同进化为算法的基本框架，各个信息要素之间的交流方式被重新建立，信息要素在蝙蝠群体与粒子群体进行转达，两个种群相互借鉴对方的优良粒子要素，使得寻优可以从局部寻优跳出来，达到全局寻优的最佳效果。因此，TB-PC算法对复杂优化问题以及大范围搜索高维度系统辨识问题特别有效。

“分而治之”思想在TB-PC算法中得以实现，将包含m个初始值的种群向量xi=[xi1,xi2,…,xid]分开为两个部分，其中mba个初始值进行单独BA算法搜索，mpso个初始值进行单独PSO算法搜索，这两个算法一起寻找全局空间，每回运算以后，蝙蝠、粒子群群体又从新合成为m行d维的向量，由适应度更换以往最优解当作两子群下一次更换的方向。扩大了寻优规模，信息要素交流传递得以加强，使算法收敛精确度和效率都得到了大幅度提高。

2.2 禁忌搜索

禁忌搜索(tabu search，TS)是对局部邻域搜索的一种扩展，是一种全局逐步寻优的算法。禁忌搜索算法中充分体现了集中和扩散两个策略，它的集中策略体现在局部搜索，即从一点出发，在这点的邻域内寻求更好的解，以达到局部最优解而结束;而为了跳出局部最优解，扩散策略通过禁忌表的功能来实现。禁忌表中记下已经到达的某些信息，算法通过对禁忌表中点的禁忌，而达到一些没有搜索的点，从而实现更大区域的搜索[8-9]。

(1) 适配值函数和初始值

本文算法适配值函数由目标函数变化而来的，就是用来测评算法寻优结果适应度函数，如式(3)所示，寻优性能完全依赖于邻域结构和初始值。TB-PC算法利用定义研究对象的稳态变化大小gd，就是相邻两次迭代适应度函数变化值，计算公式如式(8)所示，此为使禁忌触发的前提条件。

gd(t)=|goodness(t)-goodness(t-1)|

(8)

式中t=2,3,…,tmax，即为迭代次数。算法在接连10次迭代运算gd值大小都不大于0.01，就认定此时的最优值xbest就是最接近真实值的最优值，运算过程稳定，应当引进禁忌搜索且把xbest值作为初始解，记下当前迭代运算次数以及上次引进禁忌搜索迭代运算次数差值nLi，i就是为禁忌引入次数值。

(2) 禁忌表、禁忌长度和禁忌对象

设置禁忌的目的是最大可能避免迂回反复寻优，禁止重复前面工作，跳出局部最优点。禁忌表指的是被禁对象具有定长nJ且带有明确顺序进出序列的队列。禁忌长度nJ指的是被禁对象不允许被选取的迭代步数，一般是给被禁对象aj一个数lj，要求aj在lj步迭代内被禁，在禁忌表中采用Tabu(aj)=lj记忆；每迭代一步，该指标做运算Tabu(aj)=lj-1一次，直到Tabu(aj)=0时解禁。禁忌对象指的是禁忌表中被禁的那些变化元素。

TB-PC算法把蝙蝠个体群当成空间范围内一组粒子，粒子所处具体位置当作成算法一组遴选解[10]，然后由式(8)来判断引进禁忌之后，把当前最优解xbest跟禁忌表做比对，假如此全局极值和禁忌表不重合，那么xbest将会被以特定记忆顺序记录到禁忌表当中去，并被视为禁忌对象；假如此全局极值跟禁忌表重合，此全局极值禁用，接着任意在粒子群体选取另一个粒子为全局极值，这个全局极值适应度和禁忌表不重合，然后停止此次禁忌搜索，TB-PC算法正常继续寻优。最后重复以上算法过程，直到符合算法运算结束规则为止。采取先进先出的排列顺序来进行禁忌对象的替换，即是每一个禁忌对象在经历了禁忌长度nJ次运算后，又会被重新释放出来。其中，禁忌长度nJ大小由tmax和nLi所决定，多次试验之后可以选取最佳适合值。

(3)特赦准则和终止准则

在TB-PC算法中，设置特赦准则是为了使算法能够保持最佳的局部搜索效果，进而保证了较为优良的全局寻优。特赦准则的设定，包括以下三个方面：

①基于适配值的规则。若出现一个解的目标值好于前面任何一个最佳候选解，可特赦，用来提高收敛精度和速度；

②基于最小错误的规则，若所有对象都被禁忌，特赦一个适配值最小的解；

③基于影响力的规则，特赦对目标值影响最大的对象。

考虑到算法的实际操作情况，设计算法的时候不可能让禁忌长度nJ无限大，因此用终止准则来使得禁忌搜索算法的进程结束终止，且收敛近似准则就是最为常用的方法之一，包含最高要求的收敛精度、最大的迭代次数、某个最大禁忌频率和最大迭代步数等因素。本文在设计改进算法时，当迭代次数达到最大迭代次数tmax90%时候，就会当作算法终止准则条件，提高了算法稳定性和收敛精确度，同时最大程度保留了禁忌搜索的优良效果。

2.3 TB-PC算法流程

TB-PC算法的流程是由九个步骤构成，算法流程图如图1所示。

图1 TB-PC算法流程图

3 TB-PC算法性能测试

为了测试TB-PC算法全局寻优效果、避免过早收敛的性能以及群体多样性的保持能力，在此使用Shaffer、Rastrigin、Schwefel以及Rosenbrock这四个非线性的多峰值函数，用适应度、标准差和耗时这三个方面与基本的蝙蝠算法和基本粒子群算法来进行算法性能好坏的分析比较。Shaffer这个测试函数全局极值是-1，其余三个测试函数为0。

由前面的理论分析可知，TB-PC算法对初始值等参数大小设置很敏感，直接影响到算法的稳定性和精确度。此时，函数基本参数的设置如下：解群体数目m=50，蝙蝠子群mba=25，粒子群子群mpso=25，最大迭代次数tmax=1 000，搜索脉冲频率范围[-1.0,1.0]，最大脉冲频度r0=0.35，频度增大系数γ=0.07，最大脉冲音强A0=1.95，音强衰减系数α=0.9，惯性权重采用线性递减策略，从0.9递减到0.4，学习因子c1=c2=2.0，禁忌表长度nJ=10。算法重复运行10次并记录最佳适应度、标准差和算法耗时，结果如表1[6]和图2至图5所示，其中，纵坐标适应度无单位量纲，用来评价算法搜索结果。

表1 TB-PC算法测试结果

从表1 TB-PC算法测试结果和图2到图5各个函数适应度测试比较情况能够看出，对于Shaffer函数来说，在维度较低的情况下，这三种算法的适应度都能够很好的收敛到全局最优值1，寻优效果普遍较好；对于Rastrigin、Schwefel和Rosenbrock测试函数来说，对于维度较高情况下，PSO算法和BA算法适应度偏离全局最优值0很大，收敛误差大；对于维度较低Rastrigin、Schwefel函数测试下，PSO算法收敛精确度明显要比BA算法高，但是对于高维度Rosenbrock函数测试下，PSO算法收敛精度要稍微比BA算法低；TB-PC算法以协同进化和禁忌搜索为依托，使得寻优能够从局部寻优中跳出来，达到全局寻优，以上四个函数适应度普遍比较小，其收敛精度较高。

从标准差来比较分析，以上四个测试函数的标准差都是TB-PC算法最低，从中得出在10次实验测试中，TB-PC算法的成功收敛率和稳定性也都是最高的。从耗时长短来比较分析，TB-PC算法耗时比BA算法长比PSO算法短，介于二者之间。综合以上三个方面的数据分析，TB-PC算法具有以下几个优点：

(1) 全局寻优搜索性能好。TB-PC算法以协同进化和禁忌搜索为依托，结合禁忌触发准则、特赦准则和终止准则，使得寻优能够从局部寻优中跳出来，十分有效的避免局部寻优，能够达到最佳全局寻优效果。

(2)稳定性能好。TB-PC算法对以上四个测试函数的收敛精度和标准差都最低，测试结果稳定性好，对于不同维度的系统辨识问题，都能以最高的机率取得最低的标准差，系统辨识结果稳定。

(3) 收敛精度高。从表1以及图2到图5中能够看出，TB-PC算法对以上四个测试函数都有较好的收敛精度，比PSO算法、BA算法要好，并且很适合大范围高维度系统辨识问题。

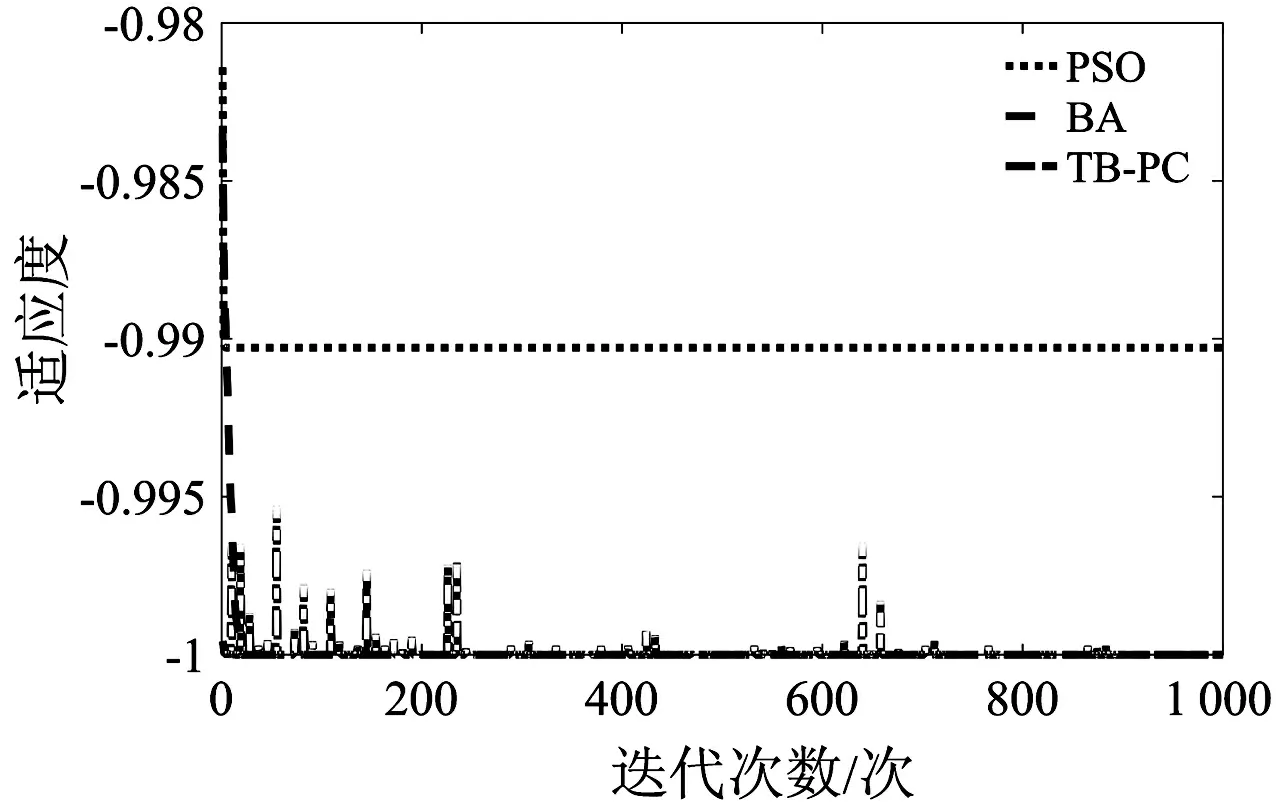
图2 Schaffer函数适应度测试比较

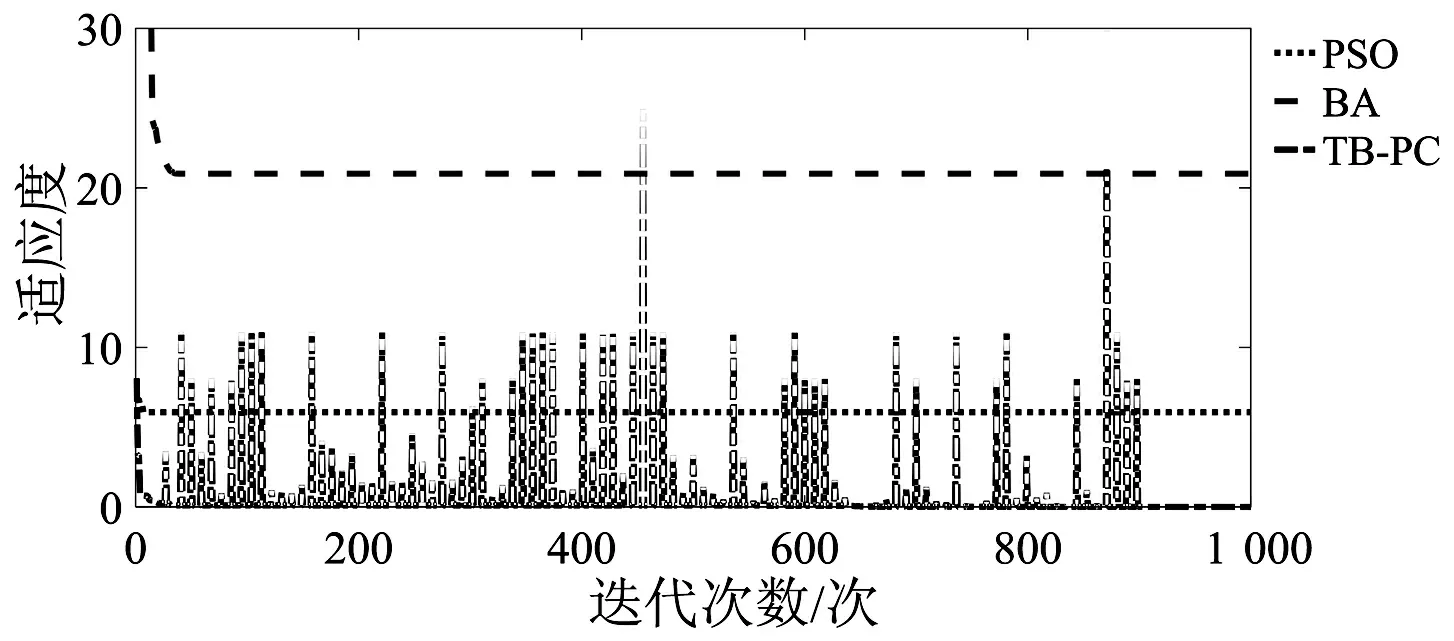
图3 Rastrigin函数适应度测试比较

图4 Schwefel函数适应度测试比较

图5 Rosenbrock函数适应度测试比较

4 MISO系统辨识仿真

构造一个带有时间延迟多输入单输出系统(MISO)传递函数，如式(9)所示：

y=G1(s)x1+G2(s)x2+G3(s)x3

(9)

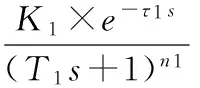
从式(9)构造出MISO系统中可以看出，这个系统由惯性环节以及比例环节组成的三输入一输出有时间延迟的多维度低阶次系统。需要辨识的结构参数是{K1,K2,K3,T1,T2,T3}，过程参数为{τ1,τ2,τ3,n1,n2,n3}。在 MATLAB中，由频域离散相似化法，把上面的传递函数模型进行离散化处理，其采样周期是1 s，共采样200组数据；将采样得到的200组数据按照传递函数模型分解的结果计算出样本的辨识数据[x1,x2,x3,y]，在[1,3]之间使用遍历法来辨识系统的各个阶次，用TB-PC算法对于不同的阶次辨识{K1,K2,K3,T1,T2,T3,τ1,τ2,τ3}的适应度大小，来比较确定待辨识系统具体各个阶次。

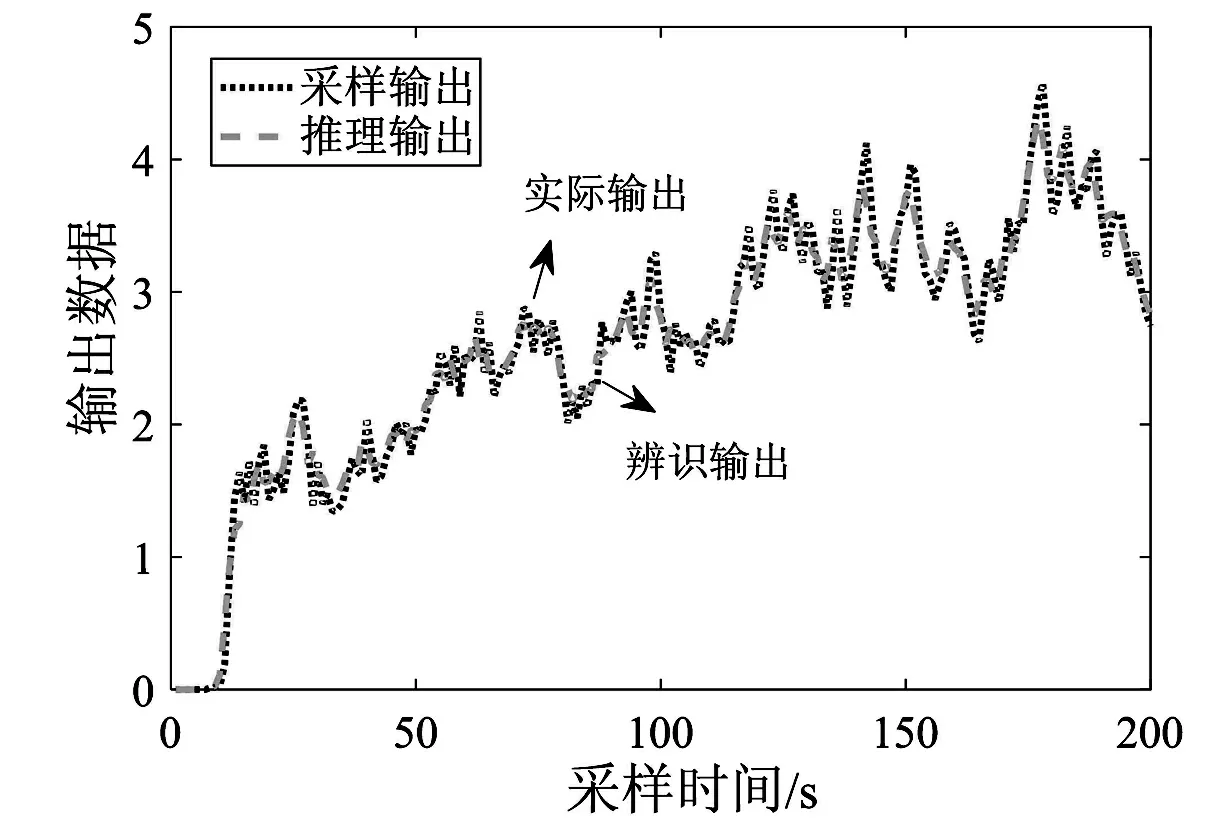
图6 辨识输出与实际输出比较

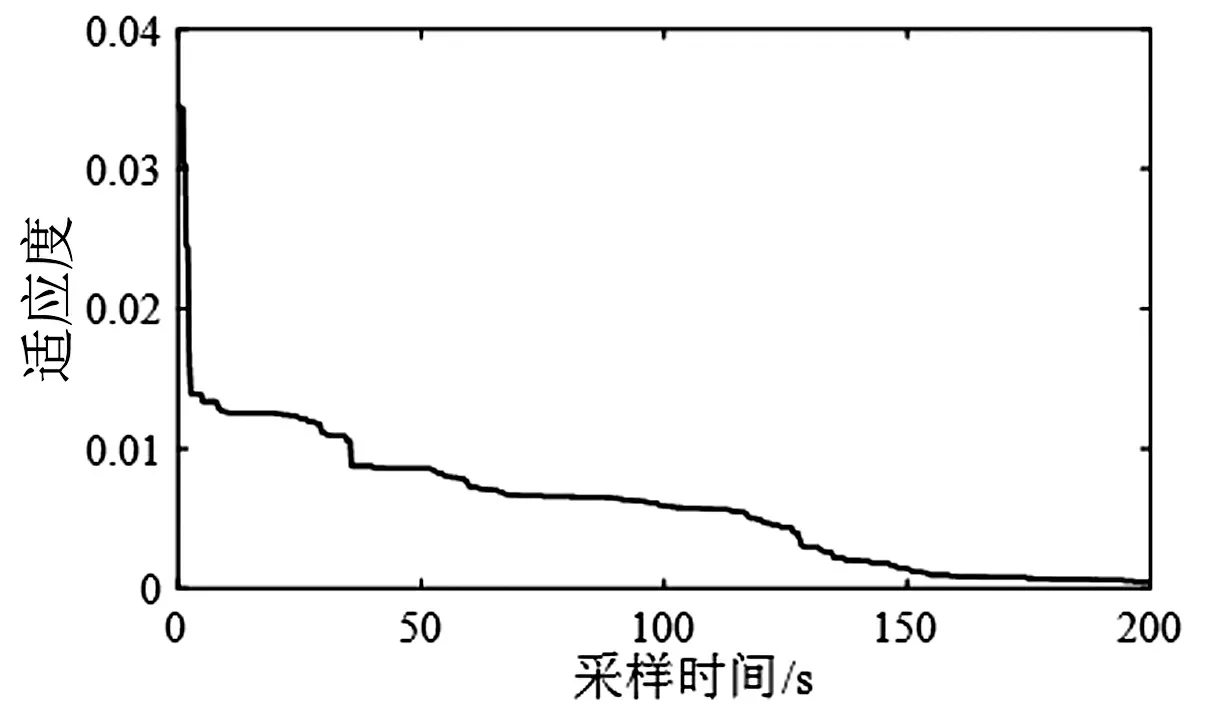
图7 TB-PC算法适应度随迭代次数变化曲线

TB-PC算法参数设置：解群体数目m=50，蝙蝠子群mba=25，粒子群子群mpso=25，最大迭代次数tmax=1000，搜索脉冲频率范围[-1.0,1.0]，最大脉冲频度r0=0.35，频度增大系数γ=0.07，最大脉冲音强A0=1.95，音强衰减系数α=0.9，惯性权重采用线性递减策略，从0.9递减到0.4，学习因子c1=c2=2.0，禁忌表长度nJ=10，反复实行10次试验得到辨识效果最好的，如式(10)所示。图6是由式(10)算法辨识结果，离散采样辨识输出数据和实际输出数据比较图，纵坐标输出数据无单位量纲，仅表示数值大小；图7为TB-PC算法适应度随迭代次数变化曲线图，纵坐标适应度无单位量纲，用来评价算法搜索结果。

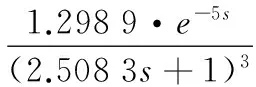
(10)

TB-PC算法辨识结果适应度为0.004 990 45，平均耗时13.884 1s，通过对真实参数与辨识结果参数比较可知，TB-PC算法对有时间延迟高维度多变量MISO系统的结构参数、过程参数以及阶次参数辨识准确度较高，全局搜索寻优性能好，辨识的系统也具有很高的收敛精度和稳定性。因此，TB-PC算法对大范围搜索高维度带时间延迟MISO系统，有优良的辨识效果。

5 结束语

本文提出了一种适用于复杂大规模带有时间延迟MISO系统模型辨识的TB-PC算法，通过对四个测试函数的测试比较，验证了TB-PC算法具有稳定性能好、收敛精度高和全局寻优搜索性能好等优点。对MISO系统进行的实例辨识仿真结果表明，TB-PC算法对其结构、过程以及阶次参数辨识准确度和适应度高，全局搜索寻优性能和稳定性好，辨识效果优良。但是其平均耗时相对较长，这是以后要加以改进和进一步研究的地方。

[ 1 ] 王建宏,王道波,王志胜.多个未知时延的MISO系统的递推辨识[J].控制与决策,2010,25(1):93-98.

[ 2 ] GAWTHROP P J, NIHTILA M T, RAD A B. Recursive parameter estimation of continuous-time systems with unknown time delay [J] .Control Theory and Advanced Technology, 2014, 5(1):227-248.

[ 3 ] BORA T C, COELHO L S, LEBENSZTAJN L. Bat-Inspired optimization approach for the brushless DC wheel motor problem[J]. IEEE Transactions on Magentics, 2015, 48(2):947-950.

[ 4 ] 李煜.新型全局优化蝙蝠算法[J].计算机科学,2013,9(40):225-229.

[ 5 ] 李枝勇,马良,张惠珍.遗传变异蝙蝠算法在背包问题上的应用[J].计算机工程与应用,2012,10(1):67-72.

[ 6 ] 张宇楠,刘付永.一种改进的变步长自适应蝙蝠算法及其应用[J].广西民族大学学报,2013,6(19):51-55.

[ 7 ] 黄宇,韩璞,刘长良.改进粒子群算法及其在系统辨识中的应用[J].中国电机工程学报,2014,51(31): 114-120.

[ 8 ] YANG XINSHE. A new metaheuristic bat-inspired algorithm[J]. Nature Inspired Coperative Strategies for Optimization,2015,7(2):65-74.

[ 9 ] 刘长平,叶明春.具有Levy飞行特征的蝙蝠算法[J]. 智能系统学报,2013,6(8):240-246.

[10] 贺一.禁忌搜索及其并行化研究[D].重庆:西南大学,2006.

Research on MISO System Identification Based on TB-PC Algorithm

Geng Jian， Zhang Yufei， Fan He

(School of Energy and Environmental，Southeast University，Nanjing Jiangsu 210096，China)

How to maintain the accuracy, convergence, time consuming and jump out of the local optimal solution of MISO system identification is a hot and difficult problem in the research. It presented a bat algorithm cooperative with particle swarm optimization based on tabu search strategy (TB-PC), analyzed control parameters, put forward reasonable frequency and initial pulse intensity, combined bat algorithm and particle swarm optimization with co-evolution together and the introduced tabu search. Through the identification and simulation of four test functions and MISO system, the results showed that the TB-PC algorithm has the advantages of good stability, high convergence precision and good identification effect on the MISO system.

TB-PC algorithm; MISO system identification; BA algorithm; PSO algorithm; co-evolution; tabu search

10.3969/j.issn.1000-3886.2017.04.006

TP273

A

1000-3886(2017)04-0018-04

定稿日期: 2016-10-26

耿健( 1991-) ，男，江苏徐州人，硕士生，研究方向为先进算法在复杂系统中建模与辨识。