基于最优比例积分的电力弹簧控制器设计
吴捷,王宝华
(南京理工大学 自动化学院,江苏 南京 210096)
基于最优比例积分的电力弹簧控制器设计
吴捷,王宝华
(南京理工大学 自动化学院,江苏 南京 210096)
电力弹簧((Electric Spring,ES)能有效缓解分布式发电系统中出现的间歇性和不稳定性问题,但是在现有控制方式下易引入谐波,且响应时间较长,严重影响了电力弹簧的调节效果。针对PI和PR控制器应用于ES这个非线性复杂系统上稳定性和鲁棒性较差的特点,应用改进的单纯型加速算法(simplex method,SPX),以时间乘以误差平方积分准则作为寻优目标函数,对PI控制器的参数进行实时调整、寻优,使ES的动态响应效果达到最佳。仿真结果表明最优PI控制器能快速、无超调的跟踪ES系统的电压设定值,具有较强的适应性和稳定性。
新能源;微电网;电力弹簧;最优PI控制;无功补偿
0 引 言
随着越来越多的风电机组接入大电网,风力发电的问题也随之凸显出来。风能的不确定性以及风机自身的运行特性使得风机的功率输出不稳定,会影响到电网的电能质量,其中电压波动和闪变是主要的负面影响[1-2]。应对分布式电源电压不稳定的问题,通常的方法是装设无功补偿器和蓄电池,但是无功装置对安装地点有严格要求,而蓄电池造价高,寿命短。
针对现有解决方法存在的问题,香港大学的Shu Yuen(Ron)Hui教授于2012年首次提出了电力弹簧(Electric Spring,简称ES)这个概念,这一理论为分布式发电系统和微电网的应用开辟了新的道路[3]1552。他深入研究了胡克定律,在电力领域提出电力弹簧的概念,其中心思想是把负载分为关键性负载与非关键性负载,电力弹簧能应对微电网中的电压波动,将关键性负载的电压稳定在目标值范围内,将电压(能量)波动传递给非关键性负载,可以有效克服新能源发电不稳定的缺点,是一种全新的控制思路[4]。
目前,对于电力弹簧的研究才刚刚开始,研究成果主要出自香港大学Shu Yuen(Ron)Hui教授的课题组,随后东南大学的程明教授也开始电力弹簧的研究。截至目前,在已发表的论文中,文献[5]在现有PI控制方式中加入了抑制谐波的环节,仿真验证其方法的有效性;文献[6]采用下垂控制策略对电力弹簧进行控制,并仿真验证了此方法的可行性;文献[7]和文献[8]将电网的扰动考虑进来,采用PR控制器结合电网电压前馈策略,制作了实验样机,实验结果表明其控制方法的有效性。但是考虑到电力弹簧ES的应用对象一般都是时变系统,而传统控制器一旦参数确定后就不会再改动,所以传统控制器很难适应对象的变化,其控制效果会受到影响。其次,受到电子元器件参数精度与数字系统精度的限制,控制器难以理论效果,并且PR控制器在非基频下增益非常小,当电网频率发生变化时,不能抑制电网引起的谐波。
针对PR控制器应用于电力弹簧ES(Electric Spring)这个非线性复杂系统上,其动态调节效果不理想的问题,本文在传统PI控制的基础上,应用以时间乘以误差平方积分准则(ITSE准则)为寻优目标函数的改进单纯型加速算法,对PI控制器的参数kp和ki进行实时调整、寻优,使电力弹簧的动态响应误差达到最小,调节效果达到最佳。仿真结果表明最优PI控制器能够快速、无超调地跟踪电压设定值,使得电力弹簧在微电网中的适应性和稳定性大大增强。
1 电力弹簧的工作原理

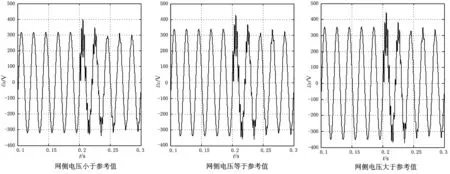
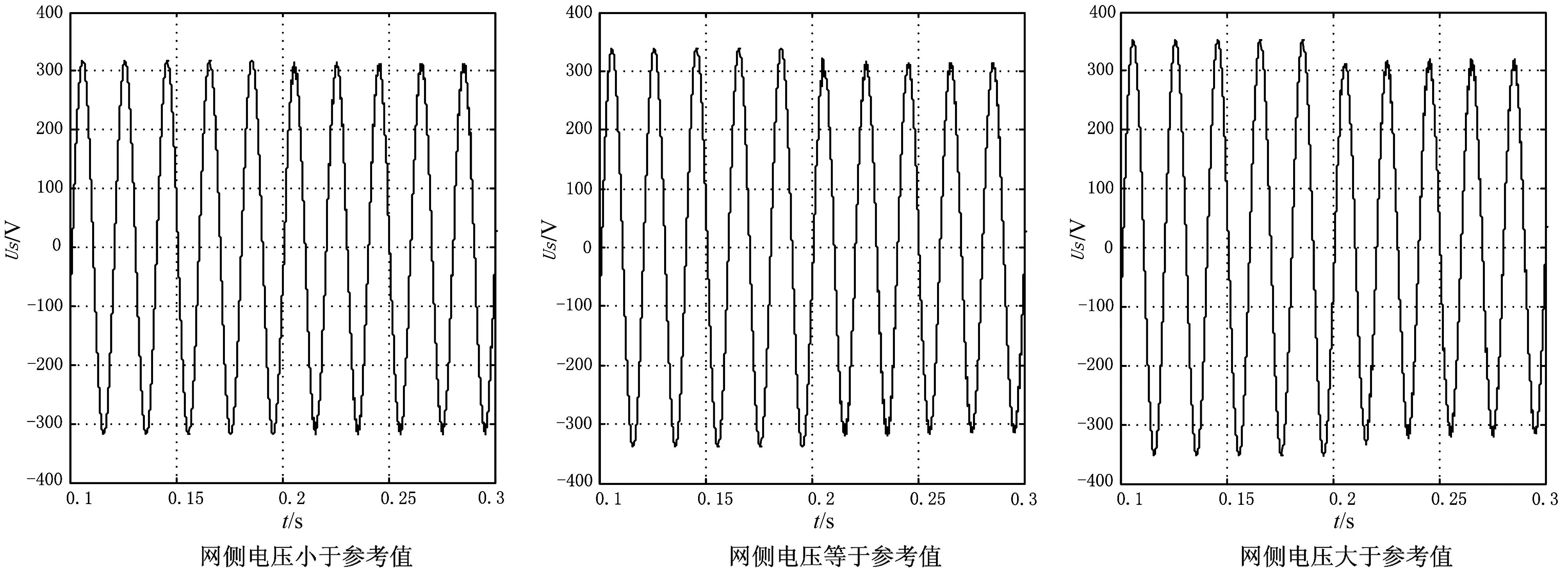
由于电网电压会在额定值上下波动,所以ES与电网之间的能量交换也会改变。根据电容C上的电压做出如下定义:当ES电压uES=0时,电路工作于阻性模式,而把此时的电网电压作为参考值;当网侧电压低于参考值时,电路工作于容性模式;当网侧电压高于参考值时,电路工作于感性模式[3]1553。
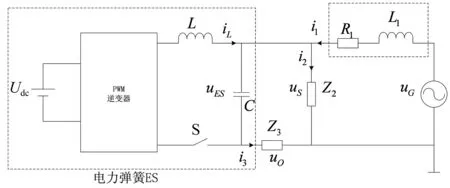
图1 电力弹簧示意图
2 ES闭环控制设计
根据图1所示的电力弹簧模型进行控制设计。图2(a)所示为电力弹簧在s域下的电路模型。通过诺顿定理将图2(a)进行简化,简化后的模型如图2(b)所示。

图2(b)中等效的参数表达式为:
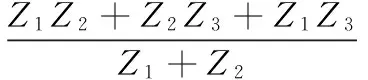
(1)
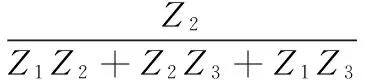
(2)
根据电路知识可知,图2(a)中有下列关系式:
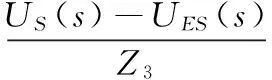
(3)
而由图2(b)可以推导得出:
(4)
联立上式(3)和式(4),解得:
US(s)=G1(s)Ui(s)+G2(s)UG(s)
(5)
式(5)中:
(6)
由式(5)可知,这是一个双输入单输出的控制系统,关键性负载上的电压由逆变电压和网侧电压共同决定,而网侧电压中的谐波对控制会有较大影响,所以在控制策略中引入前馈控制,以消除网侧电压的影响,这样电力弹簧就成了一个单输入单输出的系统,不仅有利于控制器的设计,还加快了系统的响应速度,抗扰动的能力也大大加强。所以,引入前馈的电力弹簧控制系统如图3所示。
在图3中Gx(s)表示最优PI控制器,Kpwm表示全桥逆变器的等效函数;Gn(s)则代表了前馈控制传递函数;US_ref表示关键性负载上的参考电压;US(s)表示关键性负载上的实际电压;Kvf表示反馈系数。另外,考虑到网侧电压的延时,在G2(s)后加入一个惯性环节,即图中所示的1/(1+Tds)。
如图3所示,由于前馈函数的引入,关键性负载电压将不再受网侧电压的影响,从而关键性负载电压只与Ui(s)有关,这样图3所示的控制框图就可以进行简化。在图3中,非关键性负载对网侧电压的传递函数可以求得:

(7)
为了使网侧电压对关键性负载电压的影响趋近于零,令式(7)中的分子为零,求得前馈传递函数为:
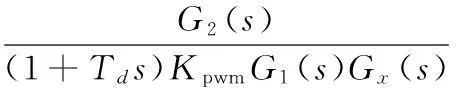
(8)
因此,简化后的系统闭环控制如图4所示。
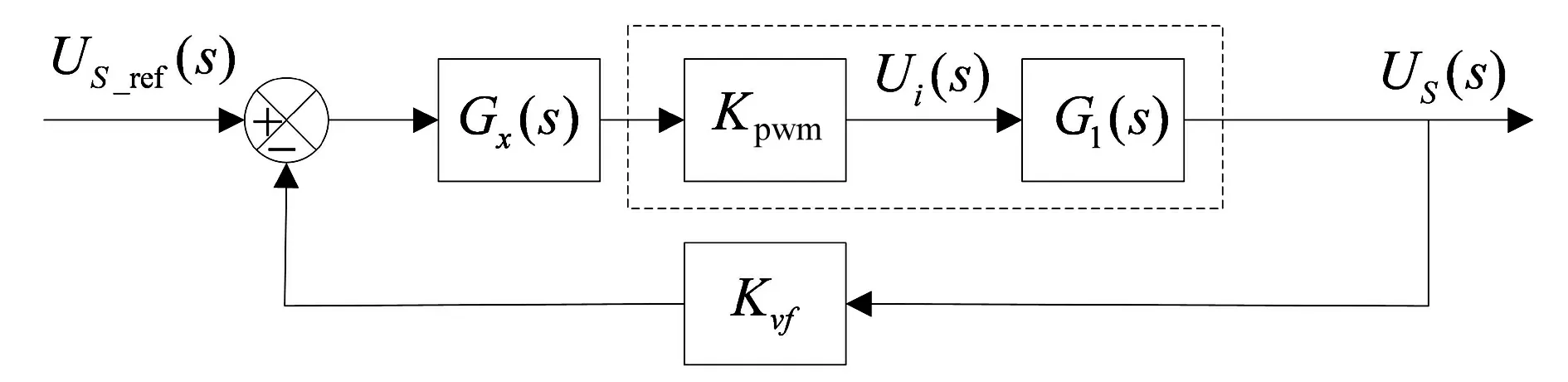
图4 简化后的闭环控制框图
求得控制系统的开环函数和闭环函数分别为:
Go(s)=KvfKpwmGx(s)G1(s)
(9)
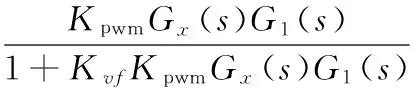
(10)
可以看出,开环函数Go(s)分子为4阶,分母为5阶,这样控制器的计算将会变得很复杂。考虑到本文采用的是寻优PI控制器,控制器对初值的精度要求并不高,所以我们进一步简化控制图,从控制的角度看,被控对象的输入是50 Hz的正弦波,输出也是50 Hz的正弦波,实际上在整个控制过程中被控对象的传递函数就是其幅频特性上50 Hz对应的增益,所以把图4中虚线框中的传递函数等效为K|s=j100π。简化后的控制系统就只有一个PI控制器,这样设计起来比较简单,进一步简化的控制框图如图5所示。
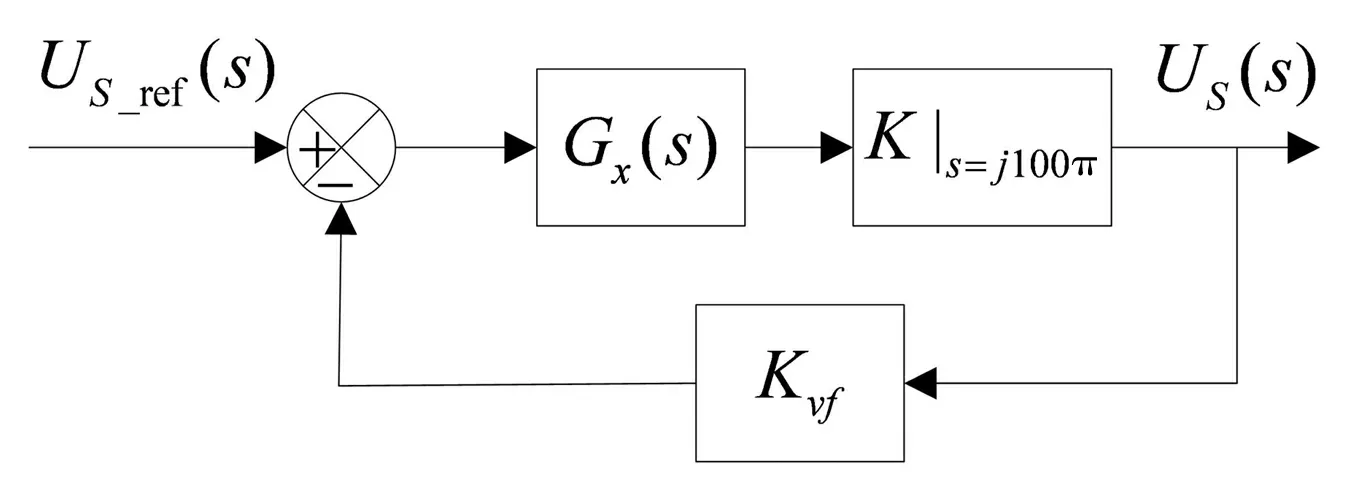
图5 进一步简化后的闭环控制框图
将PI控制器零点的频率fwz设置在100 Hz,即fwz=100 Hz,穿越频率fwc设置在10 Hz,即fwc=10 Hz,反馈系数Kvf=1。所以得到:
(11)
从上式(11)中解得kp=0.017 4,ki=10.9。至此,得到最优PI控制器的初值,接下来将对PI参数进行寻优,使电力弹簧ES的控制达到最佳。
3 单纯型最优算法

改进后的SPX(simplex method)算法与原算法的区别在于反射过程,算法中保留了原算法中向最差点发射的环节,还加入向最好点反射的环节,并在两个发射方向上选取一个更好的方向进行发射和扩张。而且采用映射单纯型方法替代原有的顶点替换法,使得单纯型在每次迭代时与初始单纯型保持一致,从而达到不退化、不降维的效果[9-10]。
步骤1:给定初始单纯型的顶点值kp1、ki1。将两个参数写成列向量的形式,并记为x(1),其它的顶点值由计算式x(i+1)=x(1)+2E(i)构造出来(i=1,2),其中E(i)代表第i个单位向量,再通过循环迭代,计算出每个顶点相对应的目标函数值,分别记为:J1、J2、J3。
步骤2:通过比较目标函数值的大小,将x重新排序得到最高点x(3)、次高点x(2)、最低点x(1),并通过检验式(12)计算结束循环。
(12)
式(12)中:J(max)是寻优的最大值点,也就是最差点;J(min)是寻优的最小值点,即最优点;ε为电压调节器的极限误差。一般ε的设定值比较小,这样可使PI调节器得到最优参数kp和ki,从而使ES动态响应的性能达到最佳。若式(12)成立,则计算结束,输出最优点x(1)和其函数值J1;若不成立,则转到步骤3。
步骤3:反射
(1)计算次高点和最低点的形心,供最高点进行反射,取反射系数γ=1.0,并计算xh(4)和Jh。
(2)计算最高点和次高点的形心,供最低点进行反射,取反射系数γ=1.0,并计算xl(4)和Jl。
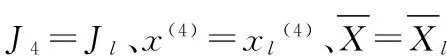
(4)若J4
步骤4:扩张。
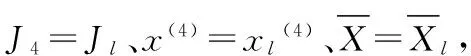
x(i)=x(TMP)+r(x(i)-x1)(i=1,2,3)
(13)
式(13)中r为映射系数,取r=1.0~1.1。
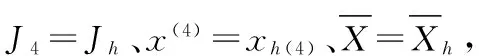
x(i)=x(TMP)+r(x(i)-x1)(i=1,2,3)
(14)
式(14)中r为映射系数,取r=1.0~1.1。
(3)转到步骤2,计算新单纯型中各顶点的目标函数值,检验是否满足收敛要求。
步骤5:若J1≤J4≤J2,则采用原有的顶点替换法,以x(1)、x(2)、x(4)构造新的单纯型,再回到步骤2计算各顶点的函数值,检验是否满足收敛要求。
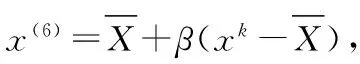
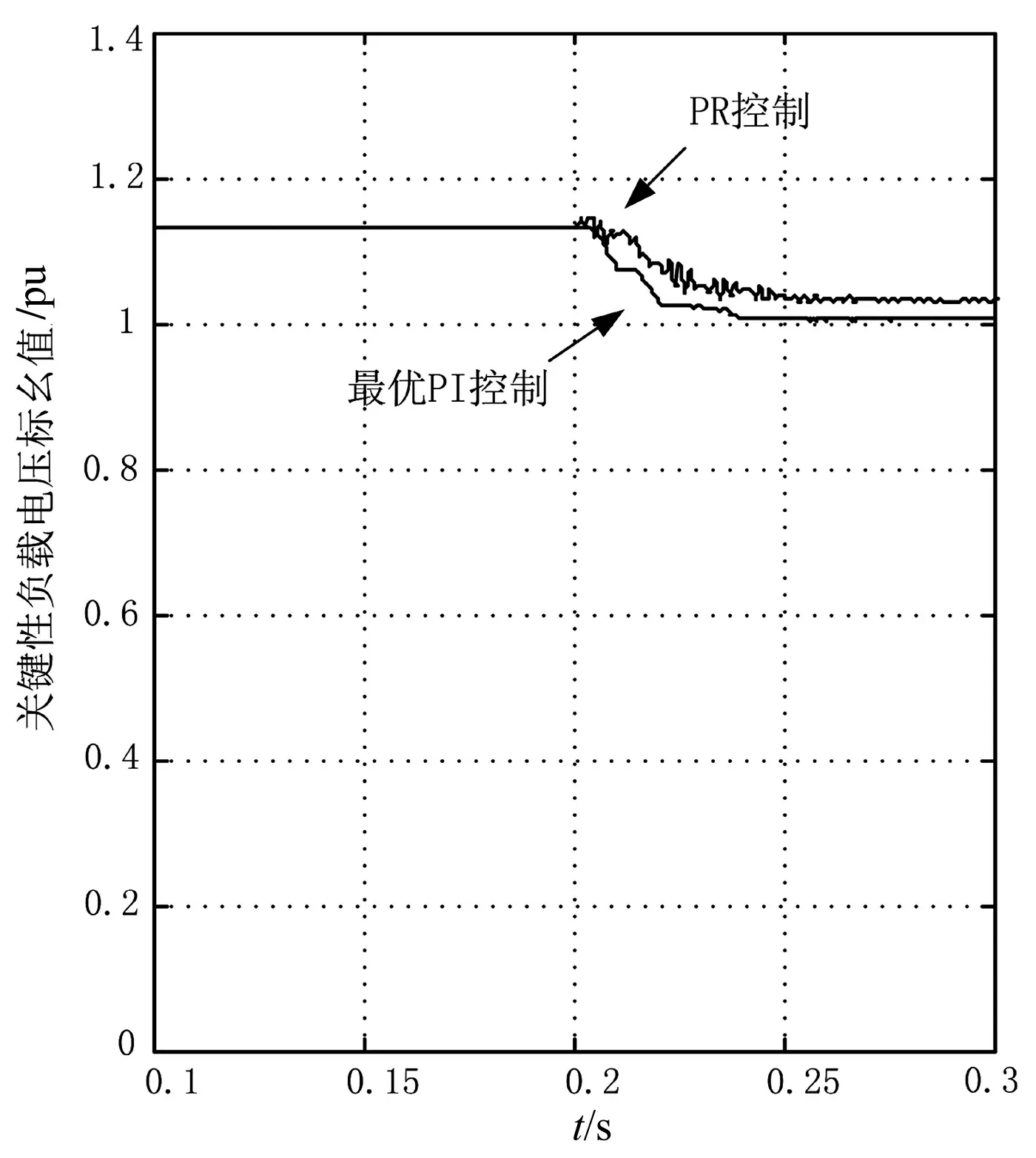
假如J6 为了验证最优PI控制器在电力弹簧稳定电压过程中的有效性,本文在MATLAB/Simulink中进行建模,改进的单纯型最优算法采用MATLAB编程。PI参数的初值为kp=0.0174,ki=10.9,计算过程见第2节。经过最优算法的寻优,最终得到kp=3.017 4,ki=13.9。仿真采用的各元件参数由表1给出。 表1 ES参数表 首先定义网侧电压的参考值,即ES中电容C电压值为0时 uG的电压值,将关键性负载上的额定工作电压定为220 V,经计算得uG=232.3 V。以0.9uG模拟网侧电压低于参考值时的情景;以1.05uG模拟网侧电压高于参考值的情景。据此为基础仿真来验证ES处于稳态时的工作状态是否与理论一致。 示波器采用三通道,分别采集uG、uS和uES的波形。图6显示的是S开关闭合前后的仿真波形。图6(b)显示的是在参考网侧电压情况下的仿真图形,此时电力弹簧工作于阻态,S闭合的时刻,uES电压值显示非常小;而图6(c)则显示了电力弹簧工作于感性模式下的图形;图6(a)显示了电力弹簧工作于容性模式下的波形。从图6中可以看出电力弹簧的使用确实可以使关键性负载电压稳定于预期值附近,这与之前的理论相一致,说明本文采用的控制方法有效。 图6 开关S闭合后 为了验证本文之前提到的采用最优PI控制器能快速跟踪的优点,本文采用比例谐振(PR)控制器作为对比,分别在三种工况下进行仿真,给出关键性负载上的电压波形,图7为采用PR控制器的仿真波形,图8为采用最优PI控制器的仿真波形。对比图7与图8,可以明显看出采用最优PI控制时效果更好,电路经过1~2个周期就能稳定,而采用PR控制器时,系统需要3~4个周期才能稳定,且控制初期时电压瞬时值会有较大的超调,不利于关键性负载的工作。 为了更好地比较两种控制器控制效果的差别,本文对关键性负载电压的标幺值进行分析,在网侧电压高于参考值的情况下进行仿真,仿真结果如图9所示。从图9中可以看出,采用最优PI控制器时,关键性负载的电压值比采用PR控制器更快地下降到关键性负载设定值。而且在采用PR控制器时,调节的初期电压有效值有少量的超调,最优PI控制器明显优于PR控制器。 图7 采用PR控制器的仿真图 图8 采用最优PI控制器的仿真图 图9 关键性负载电压标幺值 针对传统控制器动态调节效果不理想的问题,本文设计了以时间乘以误差平方积分准则为寻优目标函数的寻优准则配合电网电压前馈策略的控制方式,对电力弹簧ES进行仿真验证,得出以下结论: (1)本文的最优PI控制器能快速、无超调的跟踪电压设定值,使动态响应误差达到最小,并将网侧的电压波动传递给非关键性负载。且检验电力弹簧ES的三种工作模式,均能达到理论效果。 (2)本文采用的改进SPX寻优算法增加了搜索方向,且不退化不降维,加快了控制器的响应速度。 文本提出的用于电力弹簧的最优PI控制器不仅能有效稳定关键性负载,而且响应速度比PR控制器快,得到的瞬时调节效果也比PR控制器好。 [ 1 ] CHENG M,ZHU Y.The state of the art of wind energy conversion systems and technologies:A review[J].Energy Conversion and Management,2014,(88):332-347. [ 2 ] 孙涛,王伟胜,戴慧珠,等.风力发电引起的电压波动和闪变[J].电网技术,2003,27(12):62-66. [ 3 ] HUI S Y R,LEE C K,WU F.Electric springs—A new smart grid technology[J].IEEE Transactions on Smart Grid,2012,3(3):1552-1561. [ 4 ] LEE S C,KIM S J,KIM S H.Demand side management with air conditioner loads based on the queuing system model[J].IEEE Transactions on Power Systems,2010,26 (2):661-668. [ 5 ] PARAG KANJIYA,VINOD KHADKIKAR.Enhancing power quality and stability of future smart grid with intermittent renewable energy sources using electric springs[C]//International Conference on Renewable Energy Research and Applications.Madrid:International Journal of Renewable Energy Research,2013:918-922. [ 6 ] CHI KWAN LEE,N RAY CHAUDHURI,BALAKO CHAUDHURI,et al.Droop control of distributed electric springs for stabilizing future power grid [J].IEEE Transactions on Smart Grid,2013,4(3):1558-1566. [ 7 ] WANG Q S,CHENG M,CHEN Z,et al.Steady-state analysis of electric springs with a novel δ control[J].IEEE Transactions on Power Electronics,2015,30(12):7159-7169. [ 8 ] 程明,王青松,张建忠,等.电力弹簧理论分析和控制器设计[J].中国电机工程学报,2015,35(10):2436-2444. [ 9 ] 孔锐睿,仇汝臣,周田惠.单纯形的加速算法[J].南京理工大学学报,2003,27(2):209-213. [10] 左鹏辉,粟时平,刘桂英,等.基于改进单纯形算法的HSVS补偿系统自适应PID控制研究[J].电力电容器与无功补偿,2014,35(2):50-56. Design of an Electric Spring Controller Based on Optimal PI Wu Jie, Wang Baohua (College of Automation, Nanjing University of Science and Technology, Nanjing Jiangsu 210096, China) Electric spring (ES) can effectively relieve intermittency and instability occurring in distributed power generation systems. However, harmonics can easily be induced in the current control method with a long response time, thus seriously affecting adjustment effect of electric springs. In this paper, an improved simple type accelerating algorithm is used to overcome relatively low stability and robustness of PI and PR controllers applied in nonlinear complex system ES. In this method, integral time square error is taken as optimal goal function to adjust and optimize PI controller parameters on a real-time basis, so that ES dynamic response effect may be optimized. Simulation results show that the optimal PI controller can quickly track set voltage value of the ES system with no overshooting, and has quite good adaptability and stability. new energy; micro-grid;electric spring;optimal PI control;reactive compensation TM71 A 1000-3886(2017)04-0039-05 10.3969/j.issn.1000-3886.2017.04.012 定稿日期: 2016-09-18 吴捷(1992-),男,江西人,研究生,主要研究方向是电力系统及其自动化。 王宝华(1968-),男,江苏人,副教授,博士,主要研究方向是电力系统分析与非线性控制。4 仿真研究


5 结束语