基于ADAMS与MATLAB的Stewart次镜平台联合仿真
梁凤超,谭爽,黄刚,康建兵,林喆,康晓军
(北京空间机电研究所,北京 100094)
基于ADAMS与MATLAB的Stewart次镜平台联合仿真
梁凤超,谭爽,黄刚,康建兵,林喆,康晓军
(北京空间机电研究所,北京 100094)
Stewart平台调整次镜位姿补偿像差,是提高空间相机成像质量的有效方法。为验证Stewart次镜平台机械及控制系统的可行性、正确性、提高设计效率,基于ADAMS与MATLAB接口技术,建立了Stewart平台机械与控制系统机电混合模型,进行了机电联合仿真研究。首先,对Stewart次镜平台进行了运动学理论分析,建立了运动学数学模型;然后,在ADAMS中建立了Stewart平台虚拟样机并进行运动学仿真,ADAMS中仿真结果与理论计算一致;再将ADAMS中Stewart平台动力学模型导出并嵌入MATLAB中,建立了机电联合系统模型;最后,以典型的阶跃和正弦位姿轨迹信号,对Stewart平台的位姿调整性能进行了仿真研究。仿真结果表明,Stewart次镜平台具有较高的稳态精度和较好的动态性能,仿真参数和数据为Stewart平台的研制提供了必要的设计依据。
ADAMS;Stewart;次镜;并联机构;运动学;动力学;虚拟样机
空间相机受发射冲击、振动及在轨温度环境变化、应力释放等因素影响,可能会引起主次镜相对位置的误差及次镜倾斜,造成相机的成像质量下降。为保证主次镜光路的精确重合与对准,需要对次镜的位置与姿态做实时调整。六自由度Stewart并联机构作为次镜调整机构,具有高精度、高刚度、高稳定性,误差小、摩擦小、动态性能好等优点[1-6]。但并联机构是一个多输入、多输出系统,杆间耦合性强,控制过程复杂。在制造Stewart次镜平台的实物之前,须对并联机构机械系统和控制系统进行仿真研究,为其结构优化、控制器设计、模拟运动提供理论依据和主要参数。
传统的机电系统设计是分别设计机械和控制系统,在物理样机测试时第一次将两个设计结果结合起来,容易发生机械和控制系统不匹配问题,设计修改量大,设计效率低。因此,急需一种从设计伊始就同时考虑机械、控制系统,将二者建立在同一仿真模型中进行机电联合仿真的设计方法。联合仿真就是不同的仿真程序在同一步长时刻下交换参数和数据,然后各自进行求解计算的方法。这种方法能够有效结合多种软件的优点,实现并联机构的设计要求,提高设计的效率和质量。ADAMS可以与MATLAB之间进行控制数据交换,本文通过ADAMS/Control模块和MATLAB的接口来实现Stewart次镜平台的机电联合仿真。
1 Stewart并联机构运动学分析
并联机构运动学分析是求解并联机构的输入与输出构件之间的位置、速度、加速度之间的关系。运动学分析是进行动力学分析、结构优化设计、控制策略研究的基础。
1.1 理论基础
如图1所示,Stewart并联机构由上下两个平台和6个并联的、可独立自由伸缩的杆件组成。六根支杆和平台之间通过虎克铰Ai和球铰Bi连接,通过控制六根支杆长度来实现动平台(上平台)的位姿调整。为了定量地表示动平台各处的坐标,在静平台的综合质心处建立惯性坐标系(静坐标系)O-xyz,坐标原点为O,在上平台的综合质心处建立连体坐标系(动坐标系)P-XYZ,坐标原点为P,各坐标系的方向如图1所示。将欧拉定理中提到的刚体绕某一轴的有限转动分解为依一定顺序绕连体坐标轴的3次有限转动,则每次转过的角度可定义为确定刚体转动前后相对位置的3个广义坐标[7]。本文选取绕X→Y→Z坐标轴的顺序旋转,转动的欧拉角分别为U、V、W。经过三次旋转之后,由旋转矩阵的性质可以得到公式(1)所示的旋转变换矩阵:

其 中 ,cU=cos(U),cV=cos(V),cW=cos(W),sU=sin(U),sV=sin(V),sW=sin(W)。动平台姿态广义坐标为q=[X,Y,Z,U,V,W]T时,各支杆的长度如公式(2)所示:

其中,矢量li为图1所示的支杆矢量AiBi,li为杆长,i=1,2,…,6。至此,建立了并联机构运动学逆解数学模型。

图1 Stewart并联机构坐标系
1.2 运动学仿真
为在ADAMS中对Stewart次镜平台进行运动学仿真研究,须在ADAMS中建立Stewart次镜平台的虚拟样机模型。ADAMS提供了参数化建模功能,即将所建立模型的特征值都用ADAMS中的设计参数表示,这样,模型就会随着设计参数的修改而自动改变,大大简化了人工修改过程,特别利于机械结构的优化设计。

图2 Stewart并联机构参数化虚拟样机
在ADAMS/View中,将上铰点Bi、下铰点Ai的坐标及平台半径等设置为变量,建立了如图2所示的参数化虚拟样机模型。为模拟并联机构的运动,还需要给各个部件之间添加正确的约束。静平台与大地之间采用固定副约束,使静平台固定于大地;铰点Ai处以T型铰约束,使支杆的静杆与静平台之间只具有2个转动自由度;铰点Bi处以球型铰约束,使支杆的动杆与动平台之间只具有3个转动自由度;支杆的动杆与静杆之间以移动副约束,使二者之间只具有1个平移自由度,实现支杆的伸缩。这样,可以以此虚拟样机为基础,对Stewart次镜平台进行运动学仿真研究。
在动平台中心处同时施加六个自由度的一般点运动激励,使动平台实现沿X、Y、Z轴的移动以及沿X、Y、Z轴的旋转,以此来模拟动平台在实际工作中的一般运动。进行运动仿真后得到了如图3所示的各支杆的长度变化曲线,此即运动学逆解。再根据公式(1)、(2),应用MATLAB编程计算运动学逆解,即各支杆的实时长度。经比较,MATLAB计算支杆实时长度曲线与ADAMS仿真得到的曲线误差在10-5mm量级,说明两种模型在同一时刻,支杆的伸缩量一致,理论模型和ADAMS虚拟样机是正确的,可用此虚拟样机进行机电联合仿真。

图3 ADAMS中运动学逆解
2 Stewart次镜平台机电联合仿真
ADAMS/Control模块与MATLAB控制程序之间的联合仿真,实际上是ADAMS提供模型系统方程的参数接口,由MATLAB控制程序提供控制方案、求解控制方程;ADAMS软件可自动建立求解动力学方程[8],由ADAMS的求解器求解系统方程,在求解过程中,每经过一定时间间隔,二者进行一次数据交换。
2.1 控制策略
并联机构是个多输入多输出、高度非线性、强耦合系统,其控制问题一直是个难题。并联机构平台依靠合理并且实用的控制策略来充分发挥其性能潜力,控制策略将直接决定系统最终达到的性能指标。在实践中得到广泛应用的还是传统的PID控制算法[9],六自由度Stewart并联平台最常用的控制策略是基于铰点空间的PID控制。这种控制方法对Stewart平台的各个单通道系统分别设计PID控制器,即分别控制六个支杆完成各自既定动作来控制动平台位姿。铰点空间PID控制能够充分发挥其结构简单、调试方便的特点,使六自由度平台迅速地运行起来,因此在工程上铰点空间PID控制应用是最广泛的。
基于并联机构运动学的铰点空间PID控制框图如图4所示。控制过程为,首先根据上平台姿态的目标轨迹qr,应用运动学逆解模块计算出每个支杆的目标轨迹,即各支杆的运动学逆解杆长lir;然后lir与各支杆的实际长度相减得到杆长误差Δlir,Δlir输入到支杆各自的PID控制器,经计算得到各杆位移量指令;位移指令经驱动执行机构驱动各杆运动Δli长度;杆长位移传感器将杆长的实际值li反馈给控制器,实现各杆杆长的位置闭环控制;根据并联机构运动学逆解即平台位姿与杆长的对应关系,实现六杆驱动动平台位姿q对目标位姿qr的跟踪。
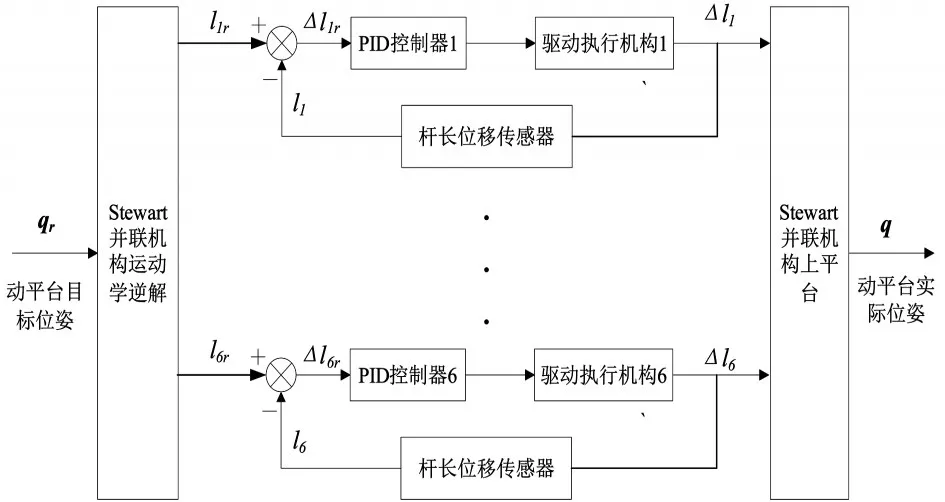
图4 并联机构铰点空间PID控制
2.2 联合仿真系统模型建立
为了进行ADAMS与MATLAB的联合仿真,实现机械系统与控制系统之间的参数传递,需要利用ADAMS/control接口模块,在ADAMS中建立联合仿真系统所需要的输入输出变量后,将ADAMS中的Stewart平台机械系统导入到MATLAB中,作为MATLAB/Simulink的—个子系统,以便在MATLAB中利用Simulink仿真模块搭建联合仿真系统,从而实现机械系统与控制系统的联合仿真。
在ADAMS中建立的变量共18个:包括6个控制杆长的杆位移变量,为平台系统的输入变量,用于接收PID控制器输出的杆长指令;6个杆长反馈变量,作为平台系统的输出变量,用于反馈六个支杆的实时长度,供MATLAB做杆长闭环控制;还有动平台位姿的6个自由度反馈变量,作为平台系统的输出变量,用于分析给定位姿与实际位姿之间的误差。

图5 联合仿真机械子系统
在MATLAB中调ADAMS/control模块,再输入命令adams_sys,MATLAB将会产生Stewart并联机构机械子系统模块,如图5所示。模块左端有6个输入变量InputDispDrive_Strut(1-6),用于接受MATLAB控制器的控制指令,右端有12个输出变量,其中Output_Strut(1-6)Length为杆长反馈值,MovPlat_(X,Y,Z,U,V,W)为动平台位姿反馈变量。
在MATLAB中建立的机电联合仿真系统模型如图6所示。Reverse Solver是Stewart次镜平台的运动学逆解计算模块,adams_sub为Stewart次镜平台机械系统。对动平台运动轨迹规划后输入目标位姿变量q=[X,Y,Z,U,V,W]T,经Reverse Solve计算得到各杆的长度Li及杆长指令与实际杆长长度误差ei=Li-Li_VP;ei经PI控制器后转化为各杆的位移指令,作为adams_sub的输入变量Input-DispDrive_Strut(i)来驱动各杆运动,从而驱动动平台运动;杆长的实际长度Output_Strut(i)Length作为adams_sub的输出变量实时反馈给Reverse Solver,经模块内部比较计算得到杆长误差ei。其中ei为杆长实时误差,Li为运动学逆解得到的各杆目标杆长,Li_VP为Stewart次镜平台各杆的实际长度,i=1,2,...,6。这样,通过对各个支杆长度的精确闭环控制,就可以实现对并联机构动平台位姿的精确控制。
2.3 机电联合仿真实验
Stewart次镜平台的作用是精确调整次镜位姿,为点到点运动,要求次镜位姿精度及位姿稳态精度高,而对于次镜运动的动态性能不做过高要求。为了对Stewart平台位姿调整性能进行验证,以位姿阶跃轨迹信号测试联合仿真系统的稳态精度,以正弦轨迹信号了解其动态性能。
图7所示为动平台在位姿阶跃信号q=[5,5,5,5,5,5]T的激励下,六支杆的位置响应曲线。从图7可以看出,在位姿阶跃信号作用下,杆1~杆6从零位开始运动到稳定在目标位置的时间分别为3.12s、3.29s、3.53s、3.46s、3.08s和3.43s,均迅速达到了稳态,且稳态值与指令值相等,无稳态误差。在ADAMS的仿真动画中可以看出,Stewart次镜平台由初始姿态迅速运动到指令给定的姿态,并稳定地保持该姿态不变。可见,杆1~杆6能够驱动动平台,在较短的响应时间内,由初始位置运动到目标位置并稳定在指令给定的目标位置。

图6 Stewart次镜平台机电联合仿真系统模型

图7 六支杆位置对阶跃信号响应曲线
当输入目标轨迹为5*sin(2*pi*0.1*t)时,即动平台3个平移自由度目标轨迹是幅值5mm、周期10s的正弦信号;3个转动自由度目标轨迹是幅值5度、周期10s的正弦信号。在此复合信号的激励下,各杆的响应曲线如图8所示。从图8的仿真曲线也可以看出,各支杆可以比较精确的跟踪给定的正弦指令,时间延迟约为0.2s,各支杆具有较好的动态特性。由图7-图8可见,Stewart平台机电联合系统具有较好的稳态和动态性能。
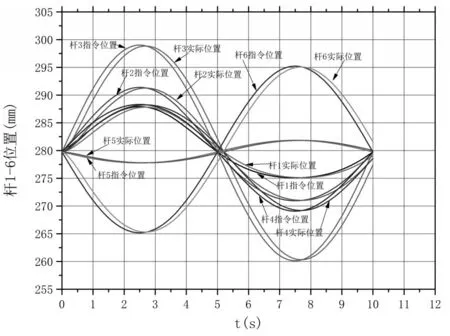
图8 动平台六杆对正弦指令的跟踪
需要指出的是:实际工程实现上,各支杆位移分辨率是有限的,仿真的理想连续运动在实际工程上是离散的运动,这会造成平台的精度受限于杆的分辨率,并且平台各自由度可能会出现耦合。因此,在工程应用的设计时,还需要根据平台位移分辨率的要求,进行支杆位移分辨率的逆解仿真,得到所需的支杆分辨率;之后再依据支杆分辨率进行正解,校核平台的位移分辨率。经过反复迭代,得到满足平台精度指标、并且工程上可实现的支杆精度要求。
3 结论
本文建立了六自由度Stewart次镜平台机电联合仿真系统,保证了机械与控制系统设计人员共享同一数据模型,避免了模型数据的不同步。以位姿阶跃轨迹信号仿真系统的稳态精度,以正弦轨迹信号仿真动态性能,仿真结果验证了基于铰点空间PID的控制策略,能够实现对六支杆的精确控制,使其快速精确定位到指令目标位置,从而实现动平台位姿的快速、精确控制。
[1]Schipani P,Perrotta F,Molfese C,et al.The VST secondary mirror support system[J].Advanced Optical and Mechanical Technologies in Telescopes and Instrumentation,2008,623(3):1-10.
[2]谭爽,王小勇,林喆,等.六自由度并联机构位姿调整灵敏度分析[J].航天返回与遥感,2015,36(3):78-85.
[3]马国庆,刘丽,于正林.一种用于并联机器人运动学求解的循环迭代方法[J].长春理工大学学报:自然科学版,2016,39(1):42-47.
[4]盖永军,潘春萍,王静泉,等.基于ADAMS的并联机构运动学仿真[J].长春理工大学学报:自然科学版,2010,33(2):71-75.
[5]赵海波,李巍,王一建.基于逆运动学的6-UPS并联机构运动学参数辨识方法[J].长春理工大学学报:自然科学版,2016,39(2):73-76.
[6]郭本银,刘钰,苗亮.六自由度微动并联机器人工作空间分析[J].长春理工大学学报:自然科学版,2015,38(4):1-5.
[7]John J.Craig.Introduction to robotics mechanics and control,Third Edition[M].Prentice Hall,2005:28-41.
[8]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2012:223-242.
[9]郭洪波.液压驱动六自由度平台的动力学建模与控制[D].哈尔滨:哈尔滨工业大学,2006.
Co-simulation of Stewart Platform for Secondary Mirror Based on ADAMS and MATLAB
LIANG Fengchao,TAN Shuang,HUANG Gang,KANG Jianbing,LIN Zhe,KANG Xiaojun
(Beijing Institute of Space Mechanics&Electricity,Beijing 100094)
In order to increase the design efficiency and verify the feasibility and correctness of the mechanical and control system of a Stewart platform for second mirror pose tuning,a co-simulation of the electro-mechanical system of the Stewart platform was studied based on the platform’s electro-mechanical model created using ADAMS and MATLAB interface technology.First,kinematics mathematical model was created using theory of inverse kinematics of the parallel mechanism.Then,the simulation of kinematics was performed after the virtual prototype of the Stewart platform was created in ADAMS,and the simulation results was consistent with the theoretical calculation.Then the model of electro-mechanical system of the Stewart platform was established by exporting the ADAMS virtual prototype and embedded it in the control model of MATLAB.Finally,performance of pose tuning was studied by using typical step and sinusoidal signals as posture trajectory of the Stewart platform.The simulation results show that the Stewart platform for the secondary mirror has a high steady accuracy and good dynamic performance,and the simulation parameters and data provide the necessary design basis for the development of the Stewart platform.
ADAMS;Stewart;secondary mirror;parallel manipulator;kinematics;dynamics;virtual prototyping
TH113.2+2
A
1672-9870(2017)04-0058-05
2016-10-24
梁凤超(1978-),男,博士,高级工程师,E-mail:fc.liang@qq.

