带加强圈外压薄壁圆柱壳体稳定性有限元分析
朱振华,崔伟,郑祥凯
(长春理工大学 机电工程学院,长春 130022)
带加强圈外压薄壁圆柱壳体稳定性有限元分析
朱振华,崔伟,郑祥凯
(长春理工大学 机电工程学院,长春 130022)
壳体在承受外压的作用时,往往因稳定性不足导致壳体的变形或者压扁,为避免壳体变形,通常在壳体外表面或内表面设置加强圈,以增加壳体的稳定性。采用有限元分析软件ANSYS对有无加强圈的薄壁圆柱壳体进行特征值屈曲分析,探究外加强圈对圆柱壳体的影响。同时针对含有不等高度、不等加强圈厚度以及不等加强圈的间距的薄壁圆柱壳体进行稳定性分析,以便以后能够设计出更加合理的加强圈满足稳定性的要求。
薄壁圆柱壳体;稳定性;加强圈;临界压力
外压壳体的失稳是指当壳体受外压作用时,外压载荷增大到某一值时,壳体会突然失去原有的形状,被压瘪或产生波纹,当载荷卸去后,壳体仍不能恢复原来的形状[1]。为避免壳体失稳变形,通常在壳体外表面或内表面设置加强圈,以增加壳体的稳定性。
目前有限元分析软件ANSYS在工程上运用比较广泛,它提供了两种分析方法,特征值屈曲分析和非线性屈曲分析(几何非线性、材料非线性)[2]。现主要采用有限元分析软件ANSYS提供的特征值屈曲分析方法对有无加强圈的外压薄壁圆柱壳体进行分析,并且利用该有限元软件提供的方法对含有不同尺寸的加强圈的圆柱壳体进行稳定性分析,探究外加强圈的尺寸对薄壁圆柱壳体失稳产生何种影响。圆柱壳分为长圆筒、短圆筒、刚性圆筒,因长圆筒失稳时出现的波纹数为2,相对于短圆筒失稳时波纹数为大于2[3],短圆筒失稳变形比较复杂,长圆筒失稳变形比较简单,因此现只探讨短圆筒的稳定性问题。
1 无加强圈的圆柱壳体有限元分析
1.1 特征值屈曲分析
特征值屈曲分析属于结构线性分析,分析简单,计算速度快。该方法不考虑初始缺陷如初始变形和应力状态,不考虑材料的非线性,虽然特征值屈曲分析经常得出非保守的结果,但还是比较接近理论计算结果的,在实际工程中运用还是比较多的[4,5]。
求解过程如图1所示:
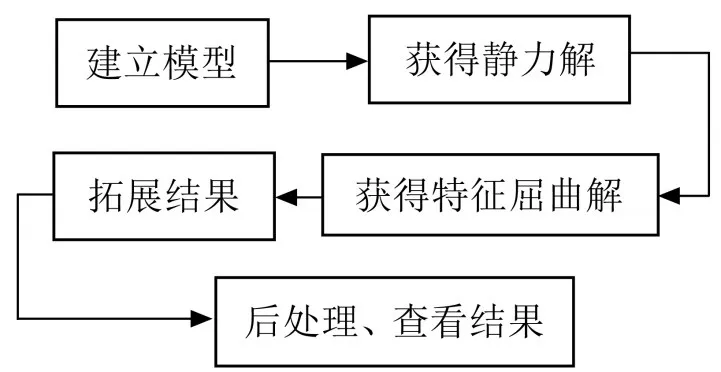
图1 特征值屈曲分析流程图
1.2 对无加强圈薄壁圆柱壳体进行分析
对于受均布外压薄壁圆柱壳体,取材质为16MnR,内径为Do=1500mm,长度L=3000mm,壁厚t=18mm的圆柱壳体。筒体采用有限元ANSYS软件提供的Shell181壳体单元[6],该单元非常适用于线性分析,壳体的厚度变化是为了适应非线性分析。约束筒体两端的非轴向位移,其中一端同时约束轴向位移[7]。其弹性模量E=210GMPa,泊松比μ=0.3。对其进行特征值屈曲分析得到的结果:4.756MPa,得到薄壁圆柱壳体失稳变形图,如图2所示。

图2 筒体失稳变形图
从图2(a)中的筒体截面图可以看出,该筒体失稳时的波形数为4,这与理论公式计算得到的波形数相一致,该方法分析出的结果还是比较准确的。从(b)图中可以观察到筒体因稳定性不足,在外压的作用下,出现明显的压邉变形。
1.3 带加强圈的圆柱壳体有限元分析
从短圆筒的临界失稳公式可知,减小圆筒的长度L或增加筒体的壁厚t,都可以提高外压圆筒的失稳临界压力Pcr,而减小L的方法是在筒体外部或内部设置加强圈[8,9]。因内外加强圈的加强原理类似,且外加强圈在实际工程上运用比较多,所以现只讨论外加强圈对壳体的加强效果。加强圈的型式很多,比如T型、扁型、半圆环壳、II型等,现主要对扁型加强圈的圆柱壳体进行稳定性分析[10],图3为带加强圈的薄壁圆柱壳体。

图3 带加强圈的薄壁圆柱壳体
加强圈与壳体可以采用连续焊接或间断焊接,有时也采用铆接,但不论采用何种焊接,必须保证其强度,不能任意削弱或割断。在壳体外部设置加强圈若采用间断焊接,其间断焊每侧焊缝的总长度不应小于壳体外圆周长的1/2。间断焊缝可以相互错开或者并排排列,其焊缝与筒体的连接如图4所示,对设置外加强圈,最大间距t=8δn(筒体的名义厚度)。
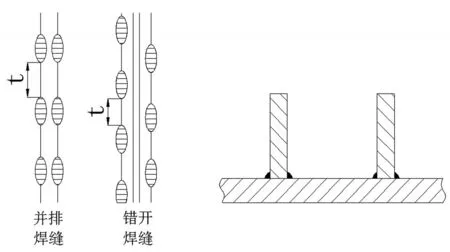
图4 焊缝与筒体连接
筒体受均布外压作用下的受力图如图5所示,设有无加强圈的筒体受到相同的外压,研究其外加强圈对筒体的影响。

表1 有无加强圈的圆筒失稳临界压力

图5 有无加强圈筒体受力图
加强圈和筒体均采用ANSYS提供Shell181单元类型,弹性模量E=210GMPa,泊松比μ=0.3,取筒体长度为L=6000mm,内径为D=1000mm,壁厚为t=10mm,加强圈的壁厚为b=20mm,加强圈的高度h=80mm,对其进行特征值屈曲分析得到的结果:4.057MPa。图6为带加强圈的圆柱壳体失稳变形图。

图6 带加强圈筒体失稳变形图
从图6带加强圈的筒体失稳变形图中的(a)、(b)可知,筒体在外压的作用下,出现明显的整体失稳。带加强圈的圆柱壳体在外压的作用下会出现两种失稳形式,加强圈段内的筒体失稳破坏和圆柱壳体整体失稳破坏,关于整体失稳和筒间的失稳也有学者研究[11],这里不再讨论。
为了探讨加强圈对筒体的加强效果,加强圈和薄壁筒体都采用ANSYS提供的Shell181单元类型,弹性模量E=210GMPa,泊松比μ=0.3。利用特征值屈曲分析确定临界失稳的压力,加强圈的壁厚、高度以及加强圈的间距取合理的数值[12],得到表1临界失稳压力。
从表1数据可知带外加强圈的薄壁圆柱壳体失稳时的临界压力远远大于无加强圈的圆柱壳体,约是无加强圈的2.5倍。这说明筒体设置加强圈能较好地提高筒体失稳时的临界压力,提高筒体的稳定性,减少因稳定性不足导致筒体的失稳破坏,因此必要时,设置加强圈是非常有必要的。
2 不同尺寸的加强圈对薄壁筒体的影响
2.1 不同高度h对薄壁筒体的影响
从上述分析结果可知设置加强圈的确可以大大提高薄壁筒体失稳时的临界压力,但是不同尺寸的加强圈对筒体的稳定性有何影响。虽然有些学者给出了设计加强圈尺寸理论计算[13],但是有时并不满足工程的实际需求,因此探究计算不同加强圈的壁厚b、不同高度h、以及不等加强圈间距Ls对薄壁筒体的影响是非常重要的。同样,加强圈和筒体均采用ANSYS提供Shell181单元类型,弹性模量E=210GMPa,泊松比μ=0.3,取筒体长度为L=6000mm,内径为D=1000mm,壁厚为t=10mm,加强圈的壁厚为b=20mm,对不同尺寸h值进行特征值屈曲分析,表2为不同高度h对应失稳时的临界压力,根据表2数据绘制失稳临界压力曲线图,如图7所示。
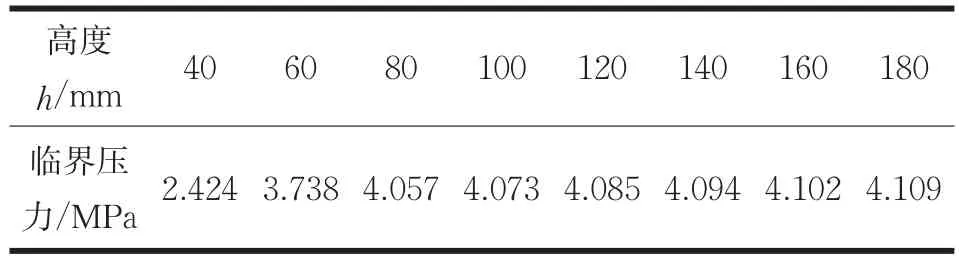
表2 不同高度h失稳时临界压力
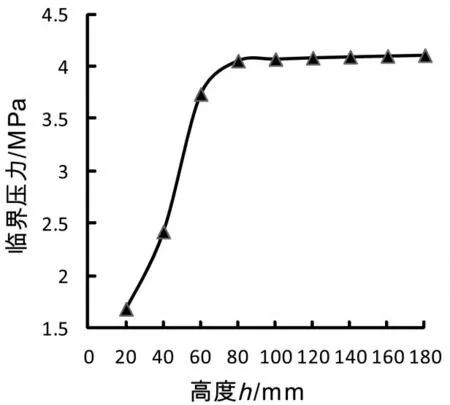
图7 不同加强圈高度h对应的临界压力
从图7可知随着加强圈高度h的增加,失稳时临界压力Pcr也随之增大,曲线上升的趋势比较显著。但增到一定的数值后,曲线逐渐趋于平缓,临界压力Pcr接近于定值。这说明在一定的高度范围内,增加加强圈的高度可以有效提高临界压力,但超过此范围增加高度对提高临界压力不明显。多数学者在对带加强圈的壳体进行稳定性分析时,也得出类似的结论。因此,在设计加强圈的高度时取合理的数值还是比较重要的,取值过高造成材料的浪费,取值过低起不到加强的效果。
2.2 不同壁厚b对薄壁筒体的影响
为探究不同壁厚b对筒体的影响,加强圈和筒体均采用ANSYS提供Shell181单元类型,弹性模量E=210GMPa,泊松比μ=0.3,取筒体长度为L=6000mm,内径为D=1000mm,壁厚为t=10mm,加强圈的高度h=80mm,取不同尺寸的加强圈壁厚b,对其进行特征值屈曲分析。得到表3对应的失稳时临界压力,根据表3数据绘制图8失稳临界压力曲线图。
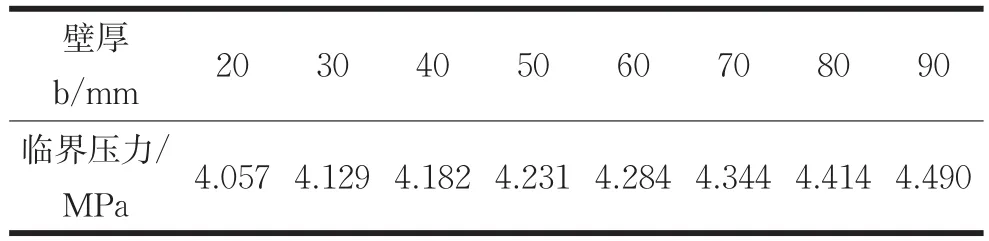
表3 不同壁厚b失稳时临界压力
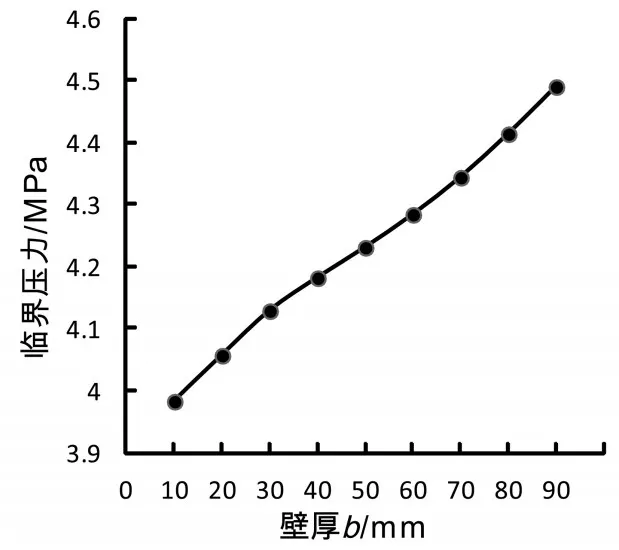
图8 不同加强圈壁厚b对应的临界压力
从图8可知随着加强圈壁厚b的增加,失稳时临近压力也随之增大,曲线呈上升的曲线,但是从数值可以看出壁厚b从10mm到90mm,临界压力才增加约0.5MPa,增量不是很显著,这与加强圈的理论结果相一致。这说明增加加强圈的壁厚确实可以提高失稳时的临界压力,但是提高的幅度不是很显著。因此,在设计加强圈的壁厚时应该取合理的数据。
2.3 不等加强圈间距对薄壁筒体的影响
为探究加强圈间距对薄壁筒体的影响,则加强圈和筒体均采用ANSYS提供Shell181单元类型,弹性模量E=210GMPa,泊松比μ=0.3,取筒体长度为L=6000mm,内径为D=1000mm,壁厚为t=10mm,加强圈的壁厚b=20mm,加强圈的高度h=80mm,取不同加强圈的间距Ls,对其进行特征值屈曲分析。得到表4对应的失稳时临界压力,根据表4数据绘制图8失稳临界压力曲线图。

表4 不同间距Ls失稳临界压力
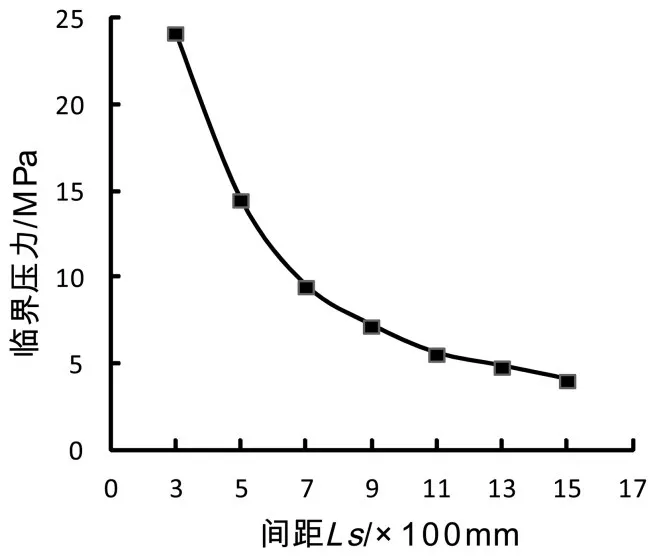
图9 不同间距Ls对应的临界压力
从图9可知随着加强圈间距Ls的增大,失稳时临界压力Pcr减小,曲线图下降的趋势比较显著。这说明减小加强圈的间距,即增加加强圈的个数可以明显地提高失稳时的临界压力。因此选择合理的加强圈的间距很重要,间距过短造成材料的浪费,间距过长起不到加强的效果。
3 结论
从上述对薄壁圆柱壳体采用有限元分析方法进行特征值屈曲分析,并且探究不同尺寸外加强圈对圆柱壳体的影响,可以得出如下结论:(1)对薄壁圆柱壳体设置合理的加强圈可以很好地提高临界压力,避免因稳定性不足导致的失稳破坏,因此合理的设置加强圈很重要。
(2)对于不同尺寸外加强圈的圆柱壳体采用特征值屈曲分析,可知加强圈的高度、壁厚以及加强圈的间距对筒体的影响不同。在一定范围内,随加强圈高度的增加,临界压力增大,但到增到一定的数值时,临界压力趋于定值。随加强圈的壁厚增加,临界压力增大,但是增大的幅度不明显。随加强圈间距的减小,临界压力增大。但是在实际中设计过程中,还是要取合理的数值,取值过大或过小都会造成材料的浪费或满足不了稳定性的要求,因此设计更为合理的加强圈的尺寸还要根据具体情况具体分析。
[1]郑津洋,董其伍,桑芝富.过程设备设计(第二版)[M].北京:化学工业出版社,2011:68-76.
[2]余军昌,徐超,张峰,等.基于ANSYS的外压圆柱壳的屈曲分析[J].轻工机械,2013,31(1):29-31.
[3]张吴星.外压薄壁短圆筒临界失稳压力理论及试验研究[J].湘潭大学自然科学学报,2001,23(2):81-83.
[4]Najafizadeh M M ,Hasani A,Khazaeinejad P.Mechanical stability of functionally graded stiffened cylindrical shells[J].Applied Mathematical Modelling,2009,33(2):1151-1157.
[5]Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression Nonlinear finite element method investigations[J].Ocean Engineering,2009,36(3/4):266-267.
[6]余伟炜,高炳军.ANSYS在机械与化工设备中的应用(第二版)[M].北京:中国水利水电出版社,2007:84-97.
[7]朱艳,王传志,董俊华,等,外压薄壁圆筒弱强结构及其临界压力的计算[J].机械强度,2016,38(4):811-815.
[8]李志义,喻健良,刘志军.过程机械[M].北京:化学工业出版社,2008:73-77.
[9]童长河,刘康林,孙太平,等,带加强圈外压柱壳的稳定性分析[J].石油化工设备,2012,41(5):28-32.
[10]田琳静,董俊华,高炳军.螺旋加强圈加强外压圆筒稳定性研究[J].机械强度,2014,36(4):566-517.
[11]杨德庆,罗放,陈静.有限元功率流落差计算方法研究[J].噪声与振动控制,2009(6):127-131.
[12]聂修民.过程装备与控制工程综合实验系统设计与研究[D].长春:长春理工大学,2012
[13]宋明晨,金志浩.外压圆筒加强圈设计[J].石油化工设备技术,1991,12(5):2-11
Finite Element Analysis of Ring-stiffened Thin-walled Cylindrical Shells Subjected to External Pressure Stability
ZHU Zhenhua,CUI Wei,ZHENG Xiangkai
(School of Mechatronic Engineering,Changchun University of Science and Technology,Changchun 130022)
When the shell receives external forces,the shell often is deformed or flattened because of lack of stability.To avoid shell deformation,usually the ring-stiffening is set in the shell outer surface or inner surface in order to increase the stability of the shell.Eigenvalue buckling analysis of thin-walled cylindrical shells with or without stiffening rings are carried out by finite element analytic software named ANSYS.The influence of outer stiffening ring on the cylindrical shells is o investigated.At the same time,the stability analysis of thin-walled cylindrical shells with unequal height,unequal thickness and unequal spacing is carried out.In order to design a more reasonable reinforcing ring,the stability requirements can be satisfied.
thin-walled cylindrical shell;stability;stiffening ring;buckling pressure
TQ320.725
A
1672-9870(2017)04-0049-04
2017-03-02
朱振华(1970-),男,硕士,副教授,E-mail:zhuzhenhua0431@163.com

