核心素养,数学课堂教学中一道亮丽的风景线
——以《椭圆的标准方程》教学设计为例
☉浙江省宁波市鄞州区正始中学 邓慧静
核心素养,数学课堂教学中一道亮丽的风景线
——以《椭圆的标准方程》教学设计为例
☉浙江省宁波市鄞州区正始中学 邓慧静
笔者于2017年1月参加了宁波市高中数学“核心素养与教学改进”论坛,以《椭圆的标准方程》教学设计为例,在课堂中渗透数学核心素养,提高了教学质量,并得到评委专家的一致肯定和赞赏,荣获宁波市一等奖.下面将演讲内容重新整理成稿,供大家参考.
一、“层峦叠嶂”——构建模型,引入课题
对于《椭圆的标准方程》这节课的引入,首先通过观察生活中常见的椭圆形状的物体让学生能够对椭圆有一个感性的认识.接着观察生活中几个常见的现象:一束光照在一个球上,一个平面去截一个圆锥,水装在倾斜的圆柱杯内.学生通过仔细观察后发现问题,提出问题:这些截面是否都是椭圆,并进一步引导学生去分析问题,满足怎样条件的图形才是一个椭圆.从而构建出椭圆的数学模型,体现了数学建模的素养.
设计意图:从生活实际出发,有利于提高学生学习的积极性,提高学习效率.让学生意识到数学不只是抽象的符号与代数,还能用来解决现实生活中的许多问题.
二、“山重水复”——动手实验,形成概念
在课题引入后,对于椭圆定义的教学,笔者设计了两个动手实验:
实验1:一支笔,一条细绳,怎么画出一个圆?
实验2:用图钉将细绳的两端固定在平面内的两点,套上铅笔,观察画出的图形是什么?
提出问题:
(1)在实验中笔尖满足什么条件?
(2)在实验过程中什么保持不变?
通过观察及实际操作,学生能够很快发现:在两次实验中,笔尖到定点的距离都等于绳子的长度,绳子的长度保持不变.
从而得出圆与椭圆的共同属性:即平面内到一个(或两个)定点的距离(或距离之和)等于定长的点的轨迹.
接着根据圆的定义:平面内到定点的距离等于定长的点的轨迹.从而类比得到椭圆的定义:平面内与两个定点的距离之和等于常数的点的轨迹.
对于椭圆的定义中难点的突破,笔者又设计了实验3与实验4.
实验3:如果绳子的长度等于两定点间的距离,观察画出的图形是什么呢?
实验4:如果细绳的长度小于两定点间的距离,是否能画出图形?
学生通过仔细观察,动手实验,从而不断完善椭圆的定义.
设计意图:在这个过程中,师生一共经历了三次抽象,第一次是从语言文字中,在理解的基础上,根据题目意思将轨迹用数学图形表示出来.之后通过动手实验,分析了绳长与定点距离不同造成轨迹不同的原因,舍弃具体的属性,抽象出椭圆的数学本质.而下定义可以视为第三次抽象,是把椭圆的本质属性用数学语言进行表述,完成了对椭圆定义的得出及定义中常数进行限制的理解.整个过程中师生共同经历概念的形成到完善,提高了学生的数学抽象素养.
三、“柳暗花明”——思维风暴,如何建系
在得出椭圆的定义后,如何建立直角坐标系,才能使所求的椭圆方程形式比较简单?
同学们展开了激烈的讨论,并提出了自己的看法,教师归纳后主要有以下几种建系方案.
方案1:以椭圆上的任意一点建立坐标系;
方案2:以F1、F2所在直线为x轴,F1或F2为坐标原点建立y轴;
方案3:以F1、F2所在直线为x轴,F1F2的中垂线为y轴.
同学们为自己提出的方案据理力争,并提出为何这样建系的理由,最后考虑到椭圆图形的美观性和对称性选择了方案3.
设计意图:在这个过程中,对于如何建系的猜想是直观想象,对数学表达式结构的优化是直观想象,将平面图形用建立坐标系后的点坐标来表示,这也是一种直观想象.通过本环节增强了学生将图形与数学代数运算相结合的能力,从而提高了学生的直观想象素养.
四、“百花齐放”——化简优化,得出方程
建立坐标系后,在求解椭圆的标准方程的过程中,如何化简方程(*),才能使运算更加简便,化简后的形式更加简单,成了学生最后运算化简的目标.
1.学生的尝试
尝试1:直接两边平方,得到(x+c)2+y2+2·+(x-c)2+y2=4a2,整理合并后,得到·=2a2-(x2+y2+c2),化简到这里,出现了两个根式相乘的形式,很多同学就不愿意再化简下去了.
尝试2:把根式比较均匀地放在等号的两边,即将(*)式中的一个根式移项,得到然后两边平方后整理合并得到a2-cx=a,两边再平方整理后得(a2-c2)x2+a2y2=a(2a2-c2),并设a2-c2=b2,即可推得椭圆的标准方程为=1(a>b>0).
上述解法也就是书本中提供的解法,虽然最后能够推导出椭圆的标准方程,但过程十分复杂,对根式进行了两次平方,那么,还有没有其他解法呢?
2.拓展解法

①2-②2得4cx=4a2(cos4α-sin4α),化简后得到cx=a(22cos2α-1),故有2acos2α=a+x,代入①式得x,两边平方,并设a2-c2=b2,即可推得椭圆的标准方程为=1(a>b>0).
评注:运用三角代换能够大大减少运算量.

无论选择②式或者③式两边再平方均可得到(a2-c2)x2+a2y2=a(2a2-c2),并设a2-c2=b2,即可推得椭圆的标准方程为=1(a>b>0).

将④式两边平方,并设a2-c2=b2,即可推得椭圆的标准方程为=1(a>b>0).
3.学生的提问
在本节课后,某学生在完成书本《普通高中课程实验标准教科书选修2-1》P41例三(即下文例题)时,能够根据题意列出等式,进而得出动点M的轨迹,这时他提出这样一个问题,为什么点M的轨迹表示椭圆?
例题 如图1,设点A,B的坐标分别为(-5,0),(5,0),直线AM,BM相交于点M,且它们的斜率之积是-,求点M的轨迹方程.

图1
分析:设点M的坐标为(x,y),那么直线AM,BM的斜率就可以用含x,y的式子表示,由于直线AM,BM的斜率之积是-,因此可以建立x,y之间的关系式,得出点M的轨迹方程.

4.学以致用
为了解决这个问题,我们对椭圆标准方程的化简过程又有了新的理解:

上式的几何意义为:动点M(x,y)到两定点A(-a,0),B(a,0)的斜率乘积等于常数m(-1<m<0)的点的轨迹为椭圆(不包括点A、B),即椭圆的第三定义.
设计意图:在一个班级中,会出现不同的算法.所谓算法多样化,就是鼓励学生独立思考,鼓励学生尝试用自己的方法进行计算.有了算法多样化,才能实现生生互动、师生互动.有了这样的运算教学,才能切实有效提高学生的数学运算素养.
五、“寒木春华”——新旧对比,教学改进
渗透了数学核心素养之后的教学目标和教学设计,与笔者在日常教学过程中所制定的教学目标及教学设计有何不同?现通过表5-1,表5-2进行对比.
1.教学目标对比(表5-1)
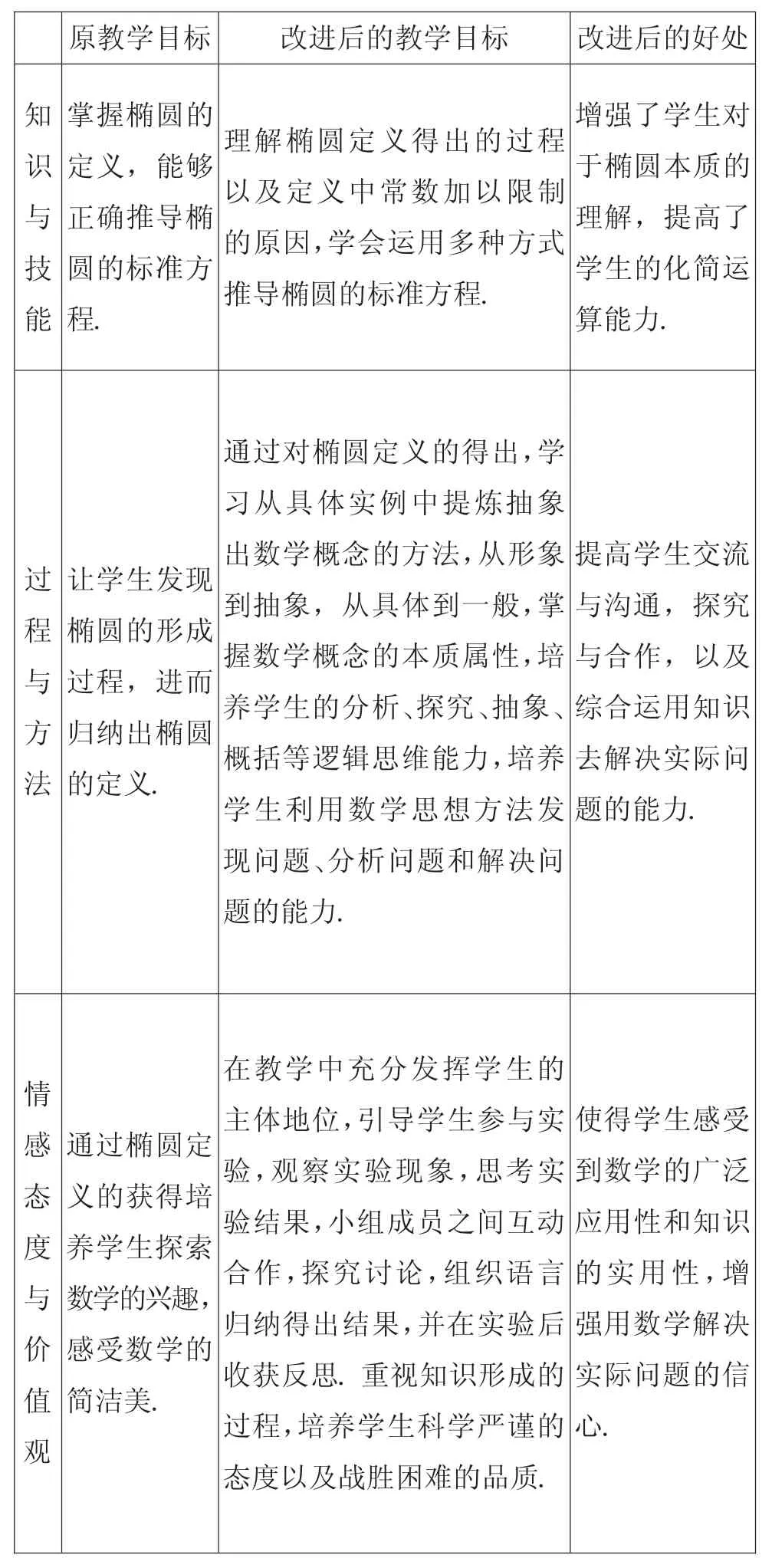
表5-1教学目标对比
2.教学设计对比(表5-2)
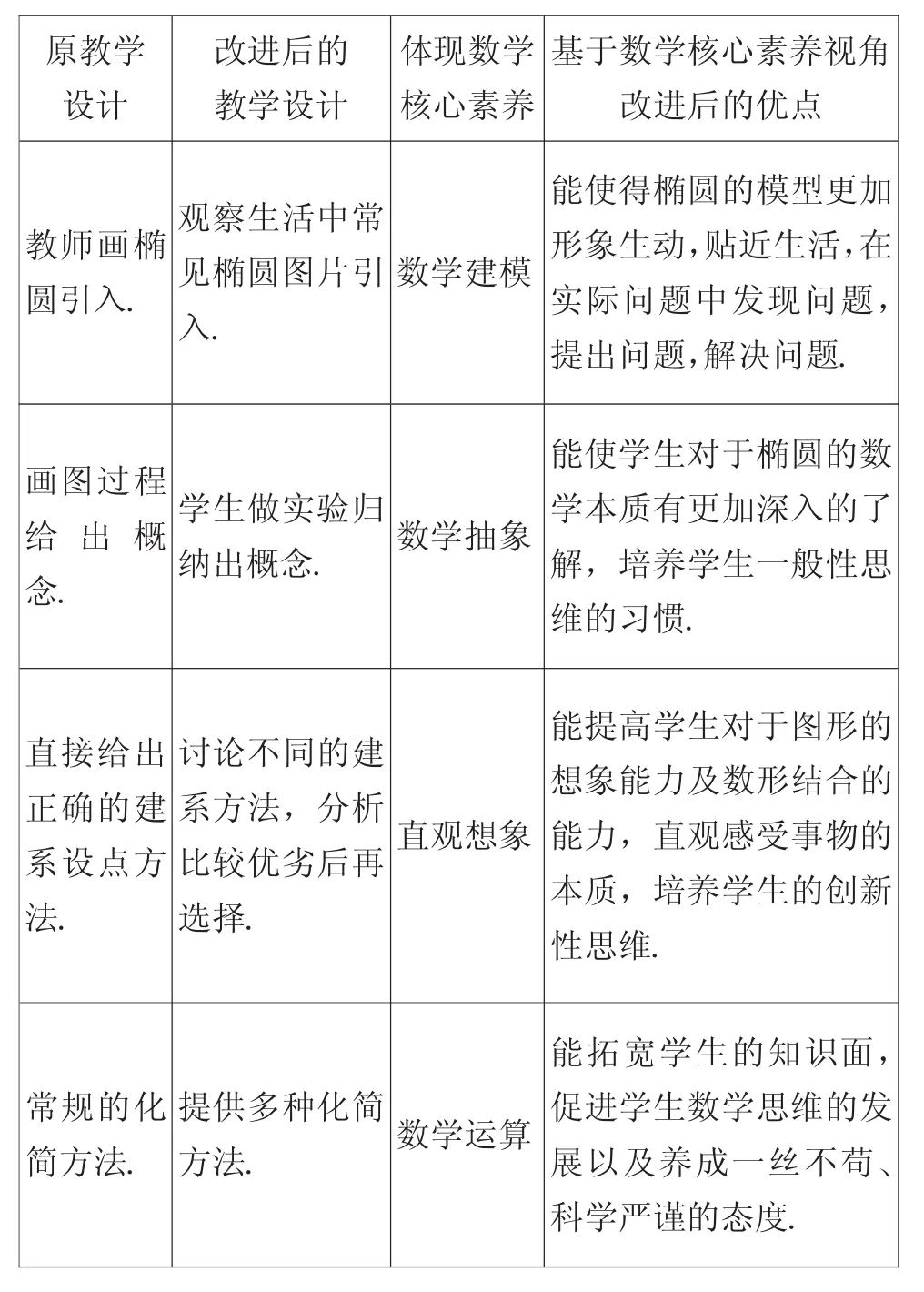
表5-2教学设计对比
六、“千山万水”——不断反思,路长且艰
1.数学素养实施的可行性
爱因斯坦曾说过:“真正的教育,不是你能获取什么知识,而是在你全都忘记以后,还剩下什么.”
“数学核心素养”就是数学基本思想的具体表现,而且最终落实到数学活动经验上,即一个人最终养成的习惯:看问题的习惯,做事情的习惯,思考问题的习惯,这些都是经验的积累,不是教出来的.因此,教师教数学的时候,要让同学们感悟出来.通过自己的思考变成自己的东西,变成一种习惯,一个人的素养养成了,习惯也就养成了.
由改进后的教学设计可知,在课堂中渗透数学核心素养是可行的.
2.数学素养实施的整体性
每一个核心素养有自身独立性,但也是一个有机联系的整体,是相互“交着”,相互“渗透”的.例如,在求解椭圆的标准方程的过程中,文字语言、符号语言和图形语言三种语言的转化就需要直观想象,逻辑推理,数学运算,数学抽象,数学建模等素养相互发挥作用才能完成.而逻辑推理贯穿于整堂课的教学始末,并与其他核心素养相互融合发挥作用,从而更好地培养学生的综合能力.
3.数学素养归根到底是一种文化素养
其实,数学素养归根到底是一种文化素养,数学教育也就是一种文化素质的教育.它的培养不是一蹴而就的,而是潜移默化,逐渐渗透的,因此教师在教导数学知识和技能教学的同时,需要运用丰富的教学手段和教学方法,有意识地培养学生的核心素养,使学生感受到,数学不仅仅是一系列抽象的知识,更多的是一种方法,一种文化,一种思想,甚至于一种精神和态度,这样才能切实有效地提高数学教学的质量.
1.任樟辉.数学思维论[M].南宁:广西教育出版社,1996.
2.郑毓信.数学方法论[M].南宁:广西教育出版社,1996.
3.史宁中.数学的抽象[J].东北师大学报(哲学社会科学版),2008(5).
4.史宁中.数学的基本思想[J].数学通报,2011(1).
5.A.D.亚历山大·洛夫,等,著.孙小礼,等,译.数学——它的内容、方法和意义[M].北京:科学出版社,2001.
6.T.丹齐克,著.苏仲湘,译.数:科学的语言[M].上海:上海教育出版社,2000.
7.斯科特,著.侯德润,张兰,译.数学史[M].桂林:广西师范大学出版社,2002.
8.章建跃.高中数学教材落实核心素养的几点思考[J].课程·教材·教法,2016(7).
9.陈建功.二十世纪的数学教育[J].中国数学杂志,1952(1).
10.周德.从《椭圆的标准方程》的教学设计中体现课标理念[J].数学教育研究,2016(4).
11.戴珣.问题情境类比探究自我评价——椭圆及其标准方程的教学设计[J].中学数学(上),2015(2).
12.杨辉军,张儒玲.整合课本资源,彰显学科魅力——话说椭圆的八个来历及应用[J].中学数学(上),2015(3).

