高中函数概念的比较研究
——以人教A版与北师大版必修1为例
☉西北师范大学教育学院 李俊彦
高中函数概念的比较研究
——以人教A版与北师大版必修1为例
☉西北师范大学教育学院 李俊彦
一、问题提出
近年来,对数学教材与课程标准进行比较研究的论文层出不穷,有进行不同年代教材比较的,如吕世虎所写的中国当代中学数学课程发展的历程及其启示;[1]也有进行中国和外国教材之间比较的,如王建磐和鲍建生从例题的背景、数学认知、运算、推理、知识综合五个因素进行其水平分析,得出中国、美国、法国、俄罗斯、澳大利亚的六套高中数学教材在例题上的难度特征.[2]
函数是中学数学新课程中的重要内容,也是高中阶段的起始课程,其概念及其思想方法贯穿了整个高中教材.高中第一节学习集合就是为了将集合作为一种数学语言来定义函数概念,进而学习后续的各种函数,函数与实际生活有着密不可分的联系,函数模型对解决现实生活中的问题至关重要.函数概念也是高中教学的重要部分,但因其自身的抽象性,学生难以理解.调查结果发现,普通高中学生对函数概念理解不够深刻.[3]为了使教师更好地教学,本文就人教版和北师大版必修1函数的概念进行比较研究,力求比较出两版本教材这一课时的异同点,以便于读者更好地熟悉和选择教材.
二、研究设计
本文主要基于人教版与北师大版课本的文本资料,采用了文本分析法与比较研究法,并进一步参考其他文献资料,进行定性分析和定量研究.
文本分析法主要是分析课程文本的一种实证研究方法,在课程研究中普遍使用,本文通过对两版本教材函数概念部分进行反复研读,先归纳出两版本教材的编排顺序与结构体系,再对其呈现方式以及本节例习题进行进一步分析;比较法则需要根据一套确定的标准对文本进行比较研究,找出文本之间的异同.文章的研究结果分为四个个部分,分别是对函数概念编排顺序的比较、函数概念结构体系的比较、函数概念内容呈现方式的比较以及例习题的比较.编排顺序、结构体系以及内容呈现方式是定性分析,编排顺序主要是比较整本教材的知识点布局,这部分将用表格的形式进行呈现;结构体系则是对函数概念一节课程教学的呈现方式进行研究,这部分采用框架图的形式进行呈现;例习题则是定量研究,引入鲍建生的综合难度模型,从五个部分比较两版本教材函数概念的例习题.
三、研究结果与分析
五个版本的普通高中课程标准实验教材中,人教版和北师大版的教材使用最广,最具代表性,下面笔者将从教材编排、课程内容结构体系、课程内容呈现方式和例习题四个方面比较分析人教版和北师大版必修1——函数的概念的异同.
1.函数概念编排顺序的比较
知识点的选取和编排都是教材知识系统中的重要的因素,教材知识点的编排顺序很大程度上影响学生按照什么样的顺序学习.我们来看一下人教版和北师大版教材的编写顺序:

图2 北师大版函数概念的编排顺序
从图1、图2我们可以看出,北师大版和人教版都是将函数的概念紧放在集合的知识之后的,不同的是,人教版将集合与函数放到了同一章,而北师大版是将函数概念及其性质单独成章.
2.函数概念结构体系的比较
根据学科的知识结构设计最佳的数学知识呈现顺序以及选取合理的数学知识是编写数学教材的主要任务.[4]《普通高中数学课程标准(实验)》(以下简称《课标》)指出:高中数学教材的编写,要根据《课标》精神,贯彻高中数学课程的基本理念与要求,教材应以课程标准中的模块为单位编写.课程标准提倡教材编写的多样化,对于各模块所规定的教学内容的编排顺序可以做适调整,不同的教材可以有自己的风格和特点.[5]下面看一下两版本具体内容结构的比较.
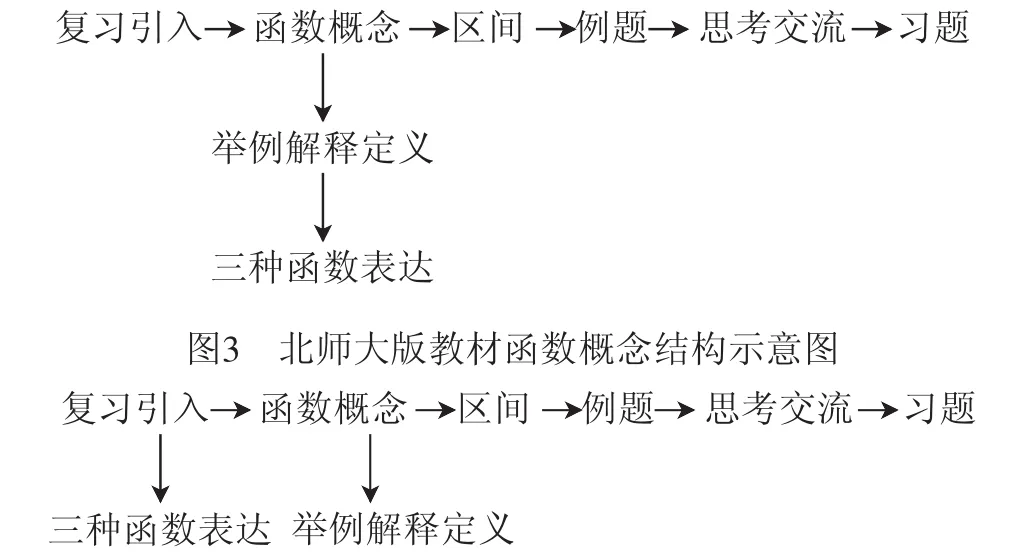
图4 人教版教材函数概念结构示意图
从图3和图4中可以看到,两版本教材的内容结构大致相同,主线大致是:引入、函数概念、区间、例题、思考交流、习题.两版本都在本节出现了函数的三种表达方式,人教版出现在引入部分,北师大版则出现在概念巩固部分.
3.函数概念内容呈现方式的比较
数学概念是数学逻辑的起点,不仅是学生的认知基础,还是学生进行数学思维的核心,在数学学习与教学中具有重要的地位,[6]数学概念的教学是学生掌握数学最基本知识点的过程,也是数学原理教学和其他数学知识教学的基础.[7]函数概念的教学大致可以归纳为以下四个步骤:提供实例、图式积累、函数概念的准备;同化顺应、抽象概括、数学概念的引入;提供变式、抽象本质、数学概念的形成;概念再同化、数学概念的深化及应用.[8]下面笔者将进一步分析两版本教材在这个步骤方面的异同.
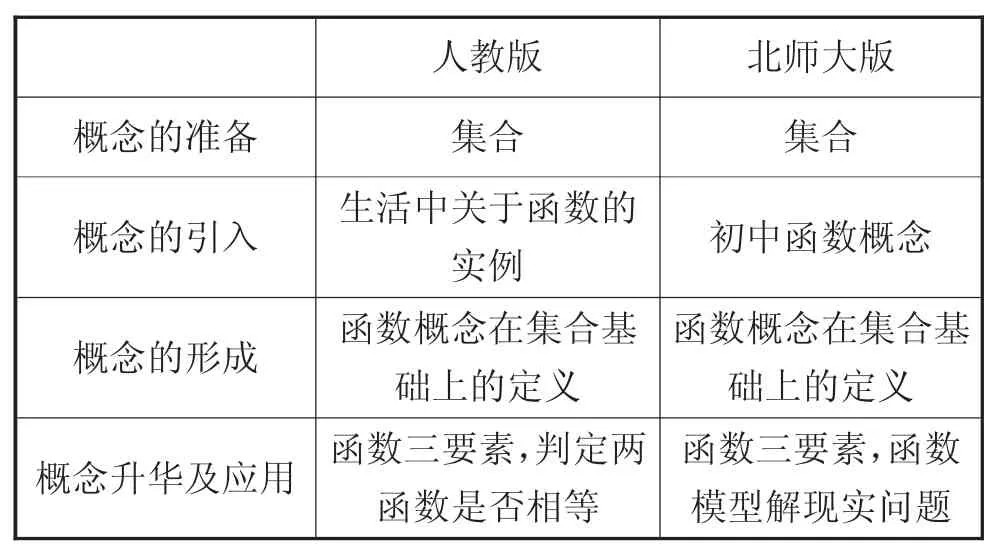
表1各版本教材函数概念的呈现方式
两版本在此小节的教学内容基本相同,其概念呈现基本上都是按照概念教学的四个步骤进行的,但是在各个步骤的处理上,仍有差别:
(1)同化顺应、抽象概括——函数概念的引入.
人教版在学习函数概念之前给出了三个生活中的现实模型,分别用函数的三种表示方法(解析式法、图像法和表格法)呈现在学生面前,在教师的引导下,让学生归纳三种函数的共同特点,借用上一节学习的集合定义,引出函数的概念;北师大版在学习函数概念之前给出了初中所学的函数概念,在对初中概念分析的基础上借用上一章所学集合的知识引出高中函数概念的定义.
(2)提供变式、抽象本质——数学概念的形成.
在函数概念定义的呈现上人教版较之北师大版更加有逻辑性,并在定义的最后提出:值域是集合B的子集.人教版在给出函数概念及函数三要素之后,紧接着给出了学生所熟悉的一次函数和二次函数的一般形式,并且给出了一次函数和二次函数一般在形式下的定义域和值域,强调了函数的唯一对应关系;北师大版则是借用了初中物理中出现的函数表达式,指出了函数的定义域和值域,并在此借用三个初中物理函数引出了函数的三种表示方法.
(3)概念再同化——数学概念的深化及运用.
人教版与北师大版的例习题都注重对函数三要素的考察,不同的是,人教版的例题中由函数概念引申出了一个新知识“判定函数的相等”;北师大版例习题则更注重讲函数概念与实际生活相联系,用函数模型解决实际问题.
4.例题及课后习题的比较
对例习题的比较主要在于对两版本教材例习题难度的分析比较,根据王建磐和鲍建生所著的《高中数学教材中例题的综合难度的国际比较》中所用的知识,笔者从背景、数学认知、运算、推理和知识综合五个方面对例、习题进行对比分析.[9]
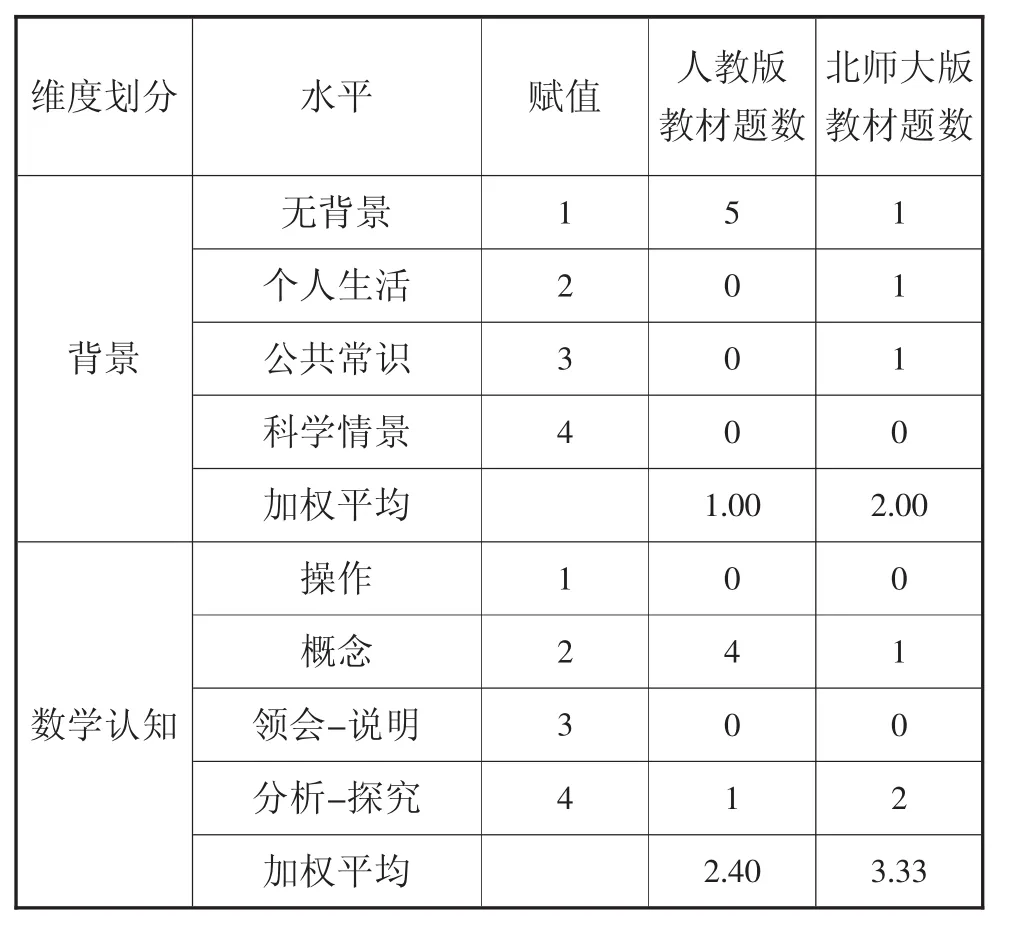
表2人教版和北师大版例习题难度因素与水平比较


图5 人教版和北师大版例习题总体水平比较
由图5可以看到,人教版和北师大版函数概念的例习题部分总体水平上有着各自鲜明的特点,两者之间存在着很大的差异.
就各自折线来看,人教版的例习题对运算的要求是最高的,加权平均值达到了2.80,其次是数学认知,加权平均值2.40,而其他三个方面则基本持平,加权平均保持在1.00左右;北师大版在数学认知上要求较高,其加权平均值高达3.33,在其他四个方面则基本持平,保持在2.00左右.相对比而言,北师大版除在运算方面加权平均低于人教版(低于40%)外,其余四个方面加权平均均高于人教版.
数据内容反映了人教版数学教材例习题在运算及数学认知方面对学生的要求较高,但在背景、推理及知识综合方面还有些欠缺;北师大版教材例习题更注重与实际生活的联系,考查学生的认知水平,各个方面考虑的更加到位.
四、研究结论与建议
(一)结论
1.两版本教材编排顺序和结构体系大体相似,但在细节处理上仍有差异
人教版和北师大版在教材编写顺序上大体相似,内容结构也大致相同,在内容的设置上都遵循了《课标》的要求,通过丰富的实例让学生体会函数是描述变量之间的依赖关系的重要模型.只是两版本教材实例出现的位置略有不同,人教版的生活模型出现在函数概念引入部分,而北师大版的生活模型则出现在函数概念给出之后,相比而言,人教版教材更满足课标中描述的“在实例的基础上学习用集合与对应语言来刻画函数”.
2.内容呈现方式上人教版重本节知识,北师大版强调整体知识联系
两版本内容呈现方式各异,人教版注重新知识本身的呈现,函数的概念整节很少涉及此节之外的其他知识;而北师大版则更注重将新知识与学生以前学习过的知识相联系起来,除本节知识之外较多涉及其他知识点.另外,在函数概念定义的呈现上,人教版更加具有逻辑性,更适合学生理解,在定义最后人教版写到:值域是集合B的子集,能够引发学生思考,同时,在概念升华阶段,人教版引入了函数相等的概念,从而使学生感悟函数的本质是对应关系.
3.例习题方面人教版偏重数学化,北师大版则偏重生活化
两版本例习题有各自的侧重性,人教版侧重于对数学基础知识的重复考查,过于强调用数学知识解决数学问题,考查知识点比较单一;北师大版则结合了更多的物理知识与实际背景,能用数学知识解决生活实际问题,考查知识点较多.总体来说,北师大版例习题难度大于人教版例习题难度.
(二)建议
1.概念引入可加入数学史的知识
在引入方面,笔者认为可以在教学中加入数学史的成分.函数的概念作为高中数学的重要概念,其发展是漫长而又曲折的,历史上,函数的概念经历了8次扩充,函数概念的每一次扩展都是对概念的不断完善的过程.高中生学习函数概念的时候或多或少也会出现像前人一样的困惑,若把历史放在他们的面前让学生了解函数概念的来龙去脉,不仅能引起学生学习函数概念的兴趣、还能帮助学习理解函数的概念,同时可以增加学生的数学文化价值.
2.让学生把握函数概念的本质特征
两版本教材都明确的说明了函数概念的定义,但要让学生深刻理解函数概念的本质,还应加入以下两点内容:①说清值域与集合B的关系.首先让学生明确值域的定义:与x值对应的y叫做函数值,值域是函数值的集合,并且,任意x∈A有唯一y∈B与之对应.下面我们用框图(图6)表示其关系:
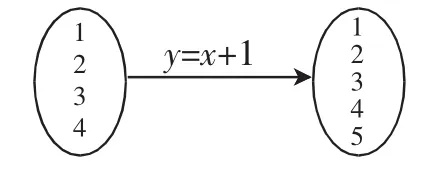
图6 函数y=x+1对应框图
图 中A={1,2,3,4},B={1,2,3,4,5}, 值 域={2,3,4,5},值域是集合B的子集得到说明.
②解释清楚函数“一对一”与“多对一”的关系,并明确提出为什么不能“一对多”.要明确任意x都有唯一y与之对应,即是说:对于同一自变量x只有一个y值与之对应,或者是多个自变量对应一个y值.教师应让学生做对应训练,加强对函数概念的理解.
例如:判断下例题目中y是否为x的函数.

3.例习题的选择要兼顾数学化和生活化
北师大版教材与实际生活联系的较为紧密,例题与习题当中均为学生提出了生活中的实际问题,从而训练了学生根据实际问题建立函数模型的能力,同时也让学生明白学习数学的作用,可以解决不少生活中的实际问题,但这样会使得学生误认为函数知识只能解决生活问题,而不是处理数学本身的问题;人教版的例习题“数学味”又太浓,应该加入一些日常生活中的函数模型.所以在列习题的选择上既要有实际生活问题又要用数学知识解决纯数学问题,二者兼顾才能更好的学习数学.同时,在例习题的设计上要注意多方面知识点的考查,不应该使一道题目的知识点过于单一.
1.吕世虎.中国当代中学数学课程发展的历程及其启示[D].东北师范大学,2009.
2.王建磐,鲍建生.高中数学教材中例题的综合难度的国际比较[J].全球教育展望,2014(8).
3.张卓颖.普通高中学生对函数概念理解程度的研究[D].吉林:东北师范大学,2006.
4.刘斌.从建构学生数学认知结构看高中教材的编写[J].课程·教材·教法,1998(5).
5.教育部.普通高中数学课程标准(实验)[M].北京.人民教育出版社,2003.
6.李善良.数学概念学习研究综述[J].数学教育学报,2001(3).
7.何小亚.数学学与教的心理学[M].广州:华南理工大学出版社,2003.
8.刘淑珍.从皮亚杰的理论谈数学概念教学[J].沙洋师范高等专科学校学报,2003(5).
9.王建磐,鲍建生.高中数学教材中例题的综合难度的国际比较[J].全球教育展望,2014(8).
10.贾随军,吕世虎,张定强,温建红.普通高中数学课程标准实验教科书人教A版与北师大版的比较研究——以“函数及其表示”为例[J].数学教育学报,2014(10).

