精彩演绎 动态生成——一节专题复习课的教学实录与分析

☉福建省厦门双十中学 彭小阳

精彩演绎 动态生成
——一节专题复习课的教学实录与分析

☉福建省厦门双十中学 彭小阳

采用何种方式上好一节复习课，是困扰广大数学老师的问题.笔者认为，有必要把“探究性复习”引入数学课堂，即教师提供相应的学习材料或设置与学习内容有关的情境，让学生先探后讲，不探不讲，即“探在讲评前，讲在关键处”.通过一题多变、一题多解等方式激活学生思维，教师适时启发、引导学生积极主动地思考、探索，做学生学习的合作者、促进者，使得教学过程成为学生自主“动态生成”知识的过程.笔者以一节放缩法专题复习课为例详细探讨，以期抛砖引玉.

一、提出问题，引发思考

师：放缩法证明数列不等式是高考数学命题的热点，通常作为试卷的压轴题，对这样的题目，请同学们谈谈自己的认识.

生：感觉技巧性太强，就像天上掉馅饼！（这时课堂上笑声四起，很多同学频频点头，说明这位同学道出了大部分同学的心声，也充分说明对放缩法进行专题研究是非常有必要的）

师：确实如这位同学所说，由于其灵活多变，许多学生觉得没有规律，无从着手，基于此，这节课就专门研究放缩法，请同学们首先证明下面的题目.

二、自主学习，独立探究

本节课，留出10分钟时间让学生独立探究，在学生自主探究中课堂非常安静，老师只是进行巡视，及时了解探究的情况，掌握反馈信息，个别询问，对学生进行个别辅导.

师：如果证不出，要考虑自己的思维障碍所在.能证出，要思考是怎么想出来的？还有无其他想法.

三、交流合作，探究解法

师：请大家谈谈自己的解法.

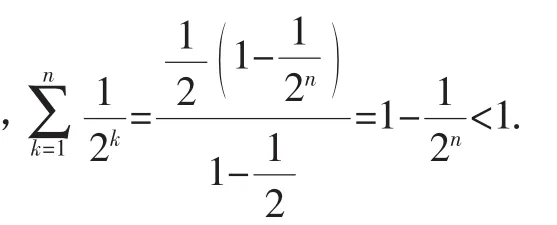
师：很好！通过观察其结构特征可直接求和，再放缩，这是最基本的放缩方法之一.第（2）问呢？

生A：第（2）问左边的和我没有求出来.

师：对，应该向可求和模型进行放缩，你是以哪个模型为目标放缩的？

师：在放缩过程中难免出现放过头的现象，遇到这种情况如果就此放弃，回头再寻找别的突破口，那就前功尽弃，能否对这个思路进行改善呢？（此言一出，使得学生重新审视这个思路）

（生C带着兴奋和激动的心情说出了自己的想法，全班顿时爆发出热烈的掌声，同学们对生C都投出了赞许的目光）

师：太好了！生C使这个思路变废为宝了！他提供了处理“放缩过头”疑难的一般解决方案——保留部分项不作处理，只对其他部分进行放缩.这种方法不妨就称之为“生C”法吧（用生C的名字命名），希望同学们将来遇到类似的困难时能利用“生C”法加以解决.

师：刚才生B与生C两位同学给出了一个很好的解法.大家想一想，对进行放大，难道只有以上这种方法吗？有没有别的方法？

师：还有别的想法吗？不一定是非常成熟的想法，有想法就大胆地表达出来.

师：生F给我们指明了解题方向，寻找表示的几何模型，哪个几何模型与n项和有关？

生G：我觉得好像与定积分有关，在定积分定义中出现过n项和……但定积分的几何意义与n个矩形面积的和有关，这里应看成什么样的n个矩形面积的和呢？（学生的思维已达到解决问题的边缘）

生H：构造出来了，n个矩形面积的和我找到了！（生H像发现新大陆似地叫了起来）

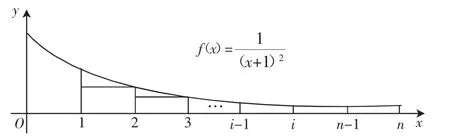
图1

师：三种方法都是从代数式结构特征出发，或变更形式或数形结合.对比发现，第三种方法创造性较强，前两种方法都是向能求和的数列模型转化.请回顾一下可求和的数列模型有哪些？

生齐答：有等差（比）模型、裂项相消模型、错位相减模型、倒序相加模型、二项式模型等.

师：如果万一出现放缩过头的情况，如何解决呢？

生齐答：可以利用“生C”法加以解决.

师：数列求和的几何意义应该往哪个方向联想？

生齐答：定积分.

四、变更原题，拓展空间

此时通过第（2）问解法探究，可谓收获颇丰.

（事实上，这个题目开始从“通项”角度思考无可厚非，也是合理的，但最后却做不出！这道题笔者本不想讲这个“做不出来的解法”，但是面对生I很合理的想法，临时决定让学生研究此解法）

师：很好，说说你下一步的想法.

（当发现自己的解法不能奏效时，生I有些尴尬，其他同学都流露出失望的表情）

师：生I的这个解法对这个题目虽然不适用，但其价值却非常大！两个数列的前n项和如果不易直接比较大小，就转而去考虑两个数列通项的大小，这种解法实质上是一种从整体到局部的思想方法.请大家用这种思路来做下面这道题目：

师：同学们非常了不起，又研究出了证明不等式的一种策略——通项法.

评注：没有任何一种解法“包解百题”，但任何一种解法都有其解题价值，即使是某种想法.

五、总结归纳，提炼升华

师：好！刚才同学们通过一道例题对放缩法做了深入的研究，研究出来不少成果，下面请同学们按班级分组讨论总结一下面临数列不等式如何进行合理放缩？一会儿请各组代表阐明自己的观点.

组1：能求和的先求和，特别是遇到一些我们熟悉的求和模型.

组2：不能求和的向能求和的方向放缩，万一放缩过头也不怕，可以用“生C”法进行调整.

组3：有的不能放缩为可求和模型，说明整体从求和角度考虑失败，可以转而从通项角度来考虑，还可以考虑数列不等式的几何特征，借助定积分来辅助思考.

本案例从两个数列不等式的证明出发，以问题为指引，以学生发展为中心，以课堂生成为目标，在教师的引导下，学生时而安静，时而活跃，时而遇到困难陷入沉思，时而探索成功雀跃激动，课堂跌宕起伏，新的生成不断涌现.仔细品味这节课，犹如陈年老酒，让人回味无穷.