给予学生一个活动空间教师收获几多意外惊喜

付光华

摘要：通过对“30°角所对直角边等于斜边一半”的证明，为学生创设思维活动的空间，使其通过多种感官的协同作用实现多渠道获得学习经验。由此培养学生积极的学习兴趣和严谨的探索精神。

关键词：初中数学；教学过程；活动

中图分类号：G633.64 文献标识码：A 文章编号：1009-010X（2017）20/23-0099-02

前苏联著名数学教育家斯托利亚尔认为：“数学教学是数学活动的教学，也是思维活动的教学。”教师要适时的给学生创设活动的空间，由学生通过动脑、动手、动口，充分调动多种感官协同活动，从多个渠道有效的获得数学活动经验。笔者依据“在直角三角形中，30。的角所对的直角边等于斜边的一半”定理证明的教学实例谈一下自己的收获与感悟，与同行交流。

问题背景：

冀教版教材八年级上册《17.2直角三角形》在“做一做”栏目安排了“证明：在直角三角形中，30°的角所对的直角边等于斜边的一半”这一题目。教材并没有给出证明方法，这就留给了教师和学生自由发挥的空间。在本课时中，教材在引出“直角三角形斜边的中线等于斜边的一半”这一定理时，采用了折纸的方法，笔者备课时，在折纸的过程中发现，能通过折叠含30°角的直角三角形纸片验证“在直角三角形中，30°的角所对的直角边等于斜边的一半”这个定理，于是在在课上处理“做一做”这个环节时有了下面的问题。

问题呈现：

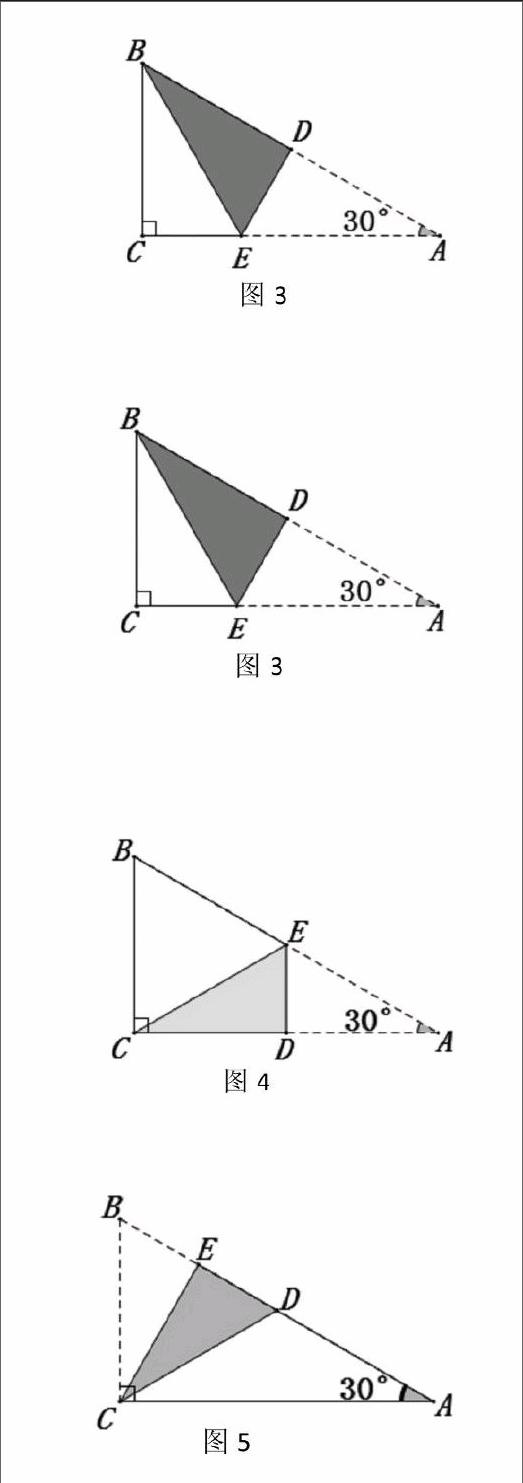
拿出事先准备好的含30°角的直角三角形纸片（如图1），要求用折纸的方法验证“在直角三角形中，30°的角所对的直角边等于斜边的一半”这一结论，有结果的先在小组内交流，然后到黑板前向全班同学分享成果。

活动实录：

学生兴趣盎然，通过动手、动脑、讨论，很快就有小组到黑板前向全体同学展示本组的研究成果。

展示一：如图2，将BC边折叠至AB边上，则LDBC=30°，因此LDBC=∠A，所以AD=BD，由“三线合一”可知：AC=BC，所以BC=AB.

展示二：如图3，把AB边对折，则∠EBD=30°，∠BDE=90°，AD=BD.所以∠CBE=60°-30°=30°.利用“角角边”可得ACBE≌ΔADBE，所以BC=BD，因此BC=1/2AB.

展示三：如图4，把AC边对折，则LECD=30°，AE=CE.所以∠BCE=90°-30°=60°，故有∠B=∠BCE=60°，所以可得ACBE为等边三角形，因此BC=BE=CE=AE，至此得到BC=1/2AB.

意外惊喜：

以上三种折法是老师课前预设就此收兵，又有学生举手示意要展示不同的折法。

展示4：如图5，将BC边折叠至CD位置（当该同学把折叠好的纸片贴在黑板上时，老师仍不以为然，因为备课时教师做过这种折法的尝试），然后这位同学又把翻折之前的部分用虚线画了出来（前几种折法不用此步），由此得∠B=∠BDC=60°，所以△ABCD是等邊三角形，即BC=BD=DC，所以LDCA=90°-60°=30°，因此∠A=LDCA，所以AD=CD，至此得到BC=1/2AB.

当这位同学展示完后，同学们自发的给出了掌声（尽管此前成绩平平，该同学对数学的学习态度变化不言而喻了）。

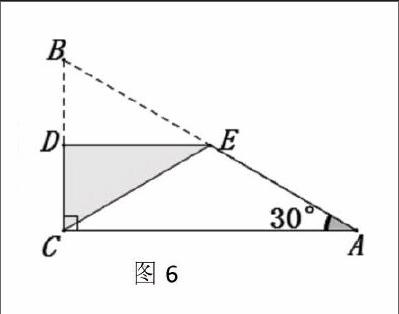
还没等老师再发感慨呢，又有同学站了起来：“要是让把没折前的图补出来，我还有不同的折法。”

展示5：如图6，将BC边对折，折痕为DE，则∠B=∠BCE=60°，所以BE=CE=BC，∠ECA=90°-60°=30°，所以CE=AE，至此得到BC=AB.

感悟与启示：

第一，数学课堂教学活动要善于创设学生思维发展的空间，让学生的思维之花绚丽绽放。课堂教学中，教师应该给学生思考的时间和空间，让学生集中注意、用足力气，运用已有的知识和生活经验去认识未知，寻求解决问题的方法和策略。在本课中，笔者自认为给学生创设了思维发展的空间，而备课时自己都没能将各种情况考虑周全，实属教师之过，庆幸的是课堂中教师耐心的等待，没有为了预设的教案而匆匆前行，课堂教学本应“以人为本”，学生是学习的主体。

第二，课堂教学教师要关注学生情绪，培养、呵护学生积极向上的心理情绪。以本节课为例，那位数学成绩平平的学生要提出自己的思路时，如果教师以时间为理由，或硬生生的说：“我觉得再没别的折法了，你的折法可能不对，下课你自己看看吧。”那么扼杀的不仅仅是一种解题方法、一个思维方式，也许是这个孩子最后一点学习数学的信心及积极思考的态度。

第三，教师要把课堂教学活动演化为学生体察良好情感的过程，获得内驱力的过程。课堂上教师应该放手让学生自己去思考探索，让学生在挑战学习困难、解决问题的过程中不断找到新的方法，获得新的发现，使能力得到提高、人格得到完善、精神得到发育和成长，这比知识本身更重要。

教师的课堂教学要着眼于学生终生发展，让学生在愉悦的情绪中思考，在思考中成长，收获并体验成长的快乐，在成长中发育精神、形成能力，为一生奠基。

【责任编辑 冯梦阳】endprint