基于忆阻的神经网络在非周期间歇性控制下的稳定化

张 腾，冯立超，何秀丽

(河海大学 理学院，江苏 南京 210098 )

基于忆阻的神经网络在非周期间歇性控制下的稳定化

张 腾，冯立超，何秀丽

(河海大学 理学院，江苏 南京 210098 )

针对具有时滞的忆阻神经网络，设计了一个非周期控制项.首先通过构造Lyapunov函数研究了在非周期间歇性控制下的稳定性问题，其次给出了获得稳定的充分条件，最后数值结果验证了结论的正确性和有效性.

神经网络； 非周期； 间歇控制； 稳定性

自从Chua[1]提出忆阻器的概念以来，忆阻器及其在神经网络方面的应用被众多学者所研究.基于忆阻的神经网络(MNNs)可以被超大规模的集成电路和由忆阻器执行的突触连接权重所实现.在一个桥路中，MNNs由一些相同的忆阻器组成，用来表现模拟乘法. 由于忆阻器记忆通过电路的电荷量的特殊能力，MNNs可以记忆其过去的动态历史.因此， MNNs的稳定性问题在科学、工程、人工神经网络(ANN)领域受到广泛的关注[2-3].但在实际操作过程中，由于神经元之间信号传播速度有限，时滞无法避免，滞后可能影响神经系统的稳定性[4-6]. 因此,时滞神经网络的控制具有理论和实际的双重重要性.许多控制方法被提出来，其中有状态反馈控制、脉冲控制、牵引控制、逐步后推控制、自适应控制、滑动模控制和间歇控制，其中，脉冲控制、部分牵引控制和间歇控制是非连续性控制. 相比连续性控制方法，非连续性控制方法更加经济有效，并且能更好的模拟真实世界，在生产制造、安全交流等领域均有广泛应用.1980年Deissenberg第一次提出间歇控制，用来控制线性计量经济模型，并且在生产制造、信息传输和安全交流等领域中不断实践，加以完善. 文献[12]通过给出几个充分条件，使得在周期间歇控制下，基于忆阻的复杂神经网络保持指数稳定.

在研究间歇控制的工作中，关于周期间歇性控制的文献[7-11]最为著名.但在一些实际应用中周期间歇性控制是十分受限制，例如，风力发电系统就是典型的非周期间歇性控制，而且周期控制也包含在非周期控制当中. 目前，只有较少文献讨论非周期间歇性控制下的神经网络的镇定问题. 例如在文献[13]中, 陈天平和刘锡伟利用非周期间歇性牵引控制，讨论了时滞耦合神经网络的同步镇定问题.关于忆阻神经网络的非周期间歇控制，尚未有人研究.因此，笔者提出了一个非周期控制项，引入到间歇控制中，使得神经网络系统更加趋于稳定，相比周期间歇性控制，此方法更加灵活，应用范围可能更加广泛.

1 模型和预备知识

1.1建立模型

考虑基于忆阻的神经网络模型

(1)

其中，

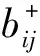
(2)

考虑控制模型(1)

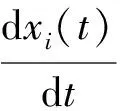
(3)

其中，di(xi(t)),aij(xi(t)),bij(xi(t))与式(1)中定义的一样，ui(t)是非周期间歇性控制下的外界输入，控制方法:对任意时间区域[ti,ti+1),t0=,i=0,1,2,…,[ti,si]是控制时间,ti和si分别表示第i个控制段的开始时间和结束时间,si-ti称作第i个控制段的控制宽度;(si,ti+1)是非控制时间,ti+1-si称作第i个控制段的非控宽度.

其中，ωi对于所有i=1,2,…,n是常量且ωi<0,则式(3)可以写成

其中，i=1,2,…,n,t≥0.

1.2预备知识要求神经网络模型( 1) 满足以下假设

则称系统(1)全局指数稳定.

定义2[13]对于非周期间歇性控制, 定义

其中,φ是指非受控时间占总的时间跨度的最大比例.

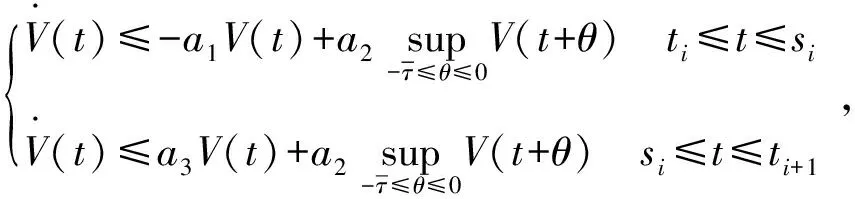
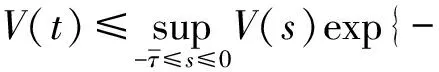
2 主要结论

通过构造Lyapunov函数，证明了受控系统的全局指数稳定性，并给出了实现稳定的充分条件.

定理1 若假设1和2成立,且存在ω1…ωn>0,0<φ<1,使得以下条件成立

1)

(4)

(5)

证明考虑Lyapunov函数

当ti≤t≤si时,对其求Dini导数可得

由假设1得

由式(2)得

当si

其中,

由式 (4)可得

又易得a2≥0,故a1>a2≥0 ，

由式 (5)可得

再由引理2可得

故受控系统全局指数稳定.

注3 与文献[13]相比较，文献[13]讨论的是在非周期间歇性牵引控制下的线性耦合神经网络的同步镇定问题，线性耦合神经网络系统为

没有涉及到忆阻神经网络,笔者将非周期间歇性控制方法推广到了忆阻神经网络上, 并得到了使之镇定的充分条件. 又可以看出, 若式(1)无切换性质, 为该系统的一个特例. 因此接下来的工作就是把耦合神经网络和非周期间歇性控制结合起来, 研究受控系统的性质, 本文所研究的仅仅是第一步.

3 数值例子

考虑带有时滞的二阶受控系统模型

4 结束语

对于基于忆阻的神经网络系统，提出了一种新的控制策略—非周期间歇控制，该控制策略通过非周期间歇性控制下的外界输入来实现.首先给出了在非周期间歇性控制下的稳定性的证明和获得稳定的充分条件，最后通过数值例子验证了结果的正确性和有效性.由注3可以看出，对非周期间歇性控制的讨论才刚刚开始，下一步工作研究非周期间歇性控制下的耦合神经网络的稳定性问题.

[1]ChuaLO.Memristor-Themissingcircuitelement[J].IEEETransactionsonCircuitTheory, 1971, 18(5):507 - 519.

[2]GuoZ,WangJ,ZhengY.Globalexponentialdissipativityandstabilizationofmemristor-basedrecurrentneuralnetworkswithtime-varyingdelays[J].NeuralNetworks, 2013,48(6):158-172.

[3]CaiZW,HuangLH,ZhuMX,etal.Finite-timestabilizationcontrolofmemristor-basedneuralnetworks[J].NonlinearAnalysisHybridSystems,2016, 20:37-54.

[4]SongQK.Exponentialstabilityofrecurrentneuralnetworkswithbothtime-varyingdelaysandgeneralactivationfunctionsviaLMIapproach[J].Neurocomputing, 2008,71(13/15):2 823-2 830.

[5]WangZD,LiuY,LiuX.Onglobalasymptoticstabilityofneuralnetworkswithdiscreteanddistributeddelays[J].PhysicsLettersA, 2005, 345(4/6):299-308.

[6]ChengCJ,LiaoTL,YanJJ,etal.Exponentialsynchronizationofaclassofneuralnetworkswithtime-varyingdelays[J].SystemsMan&CyberneticsPartBCyberneticsIEEETransactionson, 2006, 36(1):209-215.

[7]XiaWG,CaoJ.Pinningsynchronizationofdelayeddynamicalnetworksviaperiodicallyintermittentcontrol[J].Chaos, 2009, 19(1):377-385.

[8]CaiSM,LiuZ,XuF,etal.Periodicallyintermittentcontrollingcomplexdynamicalnetworkswithtime-varyingdelaystoadesiredorbit[J].PhysicsLettersA,2009,373(42):3 846-3 854.

[9]CaiSM,HaoJ,HeQ,etal.Exponentialsynchronizationofcomplexdelayeddynamicalnetworksviapinningperiodicallyintermittentcontrol[J].PhysicsLettersA,2011,375(19):1 965-1 971.

[10]GanQT.ExponentialsynchronizationofstochasticCohen-Grossbergneuralnetworkswithmixedtime-varyingdelaysandreaction-diffusionviaperiodicallyintermittentcontrol[J].NeuralNetworks,2012,31(6):12-21.

[11]HuC,YuJ,JiangH,etal.Exponentiallagsynchronizationforneuralnetworkswithmixeddelaysviaperiodicallyintermittentcontrol.[J].Chaos, 2010, 20(2):151-350.

[12]ZhangGD,ShenY.ExponentialstabilizationofMemristor-basedchaoticneuralnetworkswithtime-varyingdelaysvialntermittentcontrol.[J].IEEETransactionsonNeuralNetworks&LearningSystems, 2015, 26(7):1 431-1 441.

[13]LiuXW,ChenTP.Synchronizationoflinearlycouplednetworkswithdelaysviaaperiodicallyintermittentpinningcontrol.[J].IEEETransactionsonNeuralNetworks&LearningSystems, 2015, 26(1):113-126.

Abstract：In the report, an aperiodically control item for the memristive neural network with delays was designed. Firstly, a Lyapunov function was constructed to solve the problem of stabilization under the aperiodically intermittent control. Secondly, the sufficient conditions on stabilization were obtained. Lastly, the numerical results verified the correctness and validity of the results.

Keywords：neural network; aperiodically; intermittent control; stabilization

StabilizationofMemristor-basedNeuralNetworkviaaPeriodicallyIntermittentControl

Zhang Teng, Feng Lichao, He Xiuli

(College of Science, Hohai University, Nanjing 210098, China)

O 175

A DOl：10.15886/j.cnki.hdxbzkb.2017.0034

2016-12-28

中央高校基本科研业务费自由探索项目(2013B00614)

张腾(1991-),女,安徽桐城人,河海大学2015级硕士研究生,研究方向：忆阻神经网络的非连续性控制,E-mail:1246136755@qq.com

何秀丽(1979-),女,湖北黄冈人,博士,讲师,研究方向：随机动力系统,E-mail:hexiu00@163.com

1004-1729(2017)03-0205-06