调和p方凸函数与调和p次幂s-凸函数的定义及其判别法

沈 君

(海南师范大学 数学与统计学院, 海南 海口 571158)

调和p方凸函数与调和p次幂s-凸函数的定义及其判别法

沈 君

(海南师范大学 数学与统计学院, 海南 海口 571158)

给出了调和p方凸函数与调和p次幂s-凸函数的定义以及判定方法，建立了调和p方凸函数与调和p次幂s-凸函数的Jensen不等式

凸函数； 调和p方凸函数； 调和p次幂s-凸函数； Jensen不等式

凸函数是一类应用比较广的函数，特别在数学规划和不等式的研究中发挥着重要的作用.近年来,研究者们开始研究由凸函数延伸出来的函数类,例如:几何凸函数[1]、平方凸函数[2]、r-平均凸函数[3]、调和凸函数[4]和r次幂平均s-凸函数[5]等,给出了其延伸函数类的概念、判定定理及其应用.

f(λx1+(1-λ)x2)≤λsf(x1)+(1-λ)sf(x2),

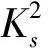
则称f(x)是I上的调和凸函数;如果不等号方向相反,则称f(x)是I上的调和凹函数.

1 调和p方凸函数定义及其判定定理

s-凸函数和调和凸函数的研究已经比较深入,特别是对Jensen不等式的研究取得了很多成果[1-7],得到了一些很有意义的结论.受此启发,笔者把调和凸函数定义中的-1次幂推广到-p次幂,提出了调和p方凸函数,又结合s-凸函数与调和p方凸函数，提出了调p和次幂s-凸函数,研究了2类凸函数类的判别法和Jensen不等式,得到一些结论,丰富了凸分析的内容.

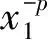
则称f(x)是区间I上的调和p方凸(凹)函数.

显然,当p=1时,调和p方凸函数就是调和凸函数.

定理1 设f(x)是定义在[a,b]⊆(0,+∞)上的正值函数,f(x)为[a,b]上调和p方凸(凹)函数的充要条件为g(x)=[f(x-1/p)]-p是[b-p,a-p]上的凹(凸)函数.

即证明了f(x)为[a,b]上调和p方凸函数.

即证明了g(x)是[b-p,a-p]上的凹函数.

证毕.

定理2 设f(x)是定义在I⊆(0,+∞)上的二阶可导的正值函数，则f(x)是I上调和p方凸(凹)函数的充分必要条件是

(p+1)x(f′(x))2-xf(x)f″(x)-(p+1)f(x)f′(x)≤0(≥0).

证明必要性 若是区间I上调和p方凸函数，由定理1知，g(x)=[f(x-1/p)]-p是I上的凹函数，即

整理上式，并把上式中x-1/p用x代替，得

.

(p+1)x(f′(x))2-xf(x)f″(x)-(p+1)f(x)f′(x)≤0.

充分性 将必要性证明过程逆推即得充分性的证明过程.

证毕.

2 调和p次幂s-凸函数的定义及其判别定理

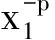
则称f(x)是区间I上的调p和次幂s-凸(凹)函数.

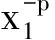
从而证明了f(x)是区间I上的调和p次幂s-凸函数.

因此g(x)为I-p上的s-凹函数.

证毕.

(x3-x2)s(f(x1))-p-(x3-x1)s(f(x2))-p+(x2-x1)s(f(x3))-p≥0(≤0) .

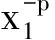
把λ代入上式,整理即可得.

(x3-x2)s(f(x1))-p-(x3-x1)s(f(x2))-p+(x2-x1)s(f(x3))-p≥0 .

充分性 上述证明过程逆推即可得充分性成立.

证毕.

(p+1)x(f′(x))2-xf(x)f″(x)-(p+1)f(x)f′(x)≥0

成立,则f(x)是区间I上的调和p次幂s-凹函数.

t(f(x1))-p≤ts(f(x1))-p,(1-t)(f(x2))-p≤(1-t)s(f(x2))-p

成立，从而

(t(f(x1))-p+(1-t)(f(x2))-p)-1/p≥[ts(f(x1))-p+(1-t)s(f(x2))-p]-1/p，

由已知条件知f(x)是I上的调和p方凹函数，即有

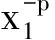
即证明了f(x)是区间I上的调和p次幂s-凹函数.

同理可证，若f(x)是区间I上的调和p次幂s-凸函数,则f(x)是区间I上的调和p方凸函数.

3 调和p方凸函数的Jensen不等式

建立了调和p方凸(凹)函数的离散型和积分型Jensen不等式.

证明只证f(x)是调和p方凸函数的情况，当f(x)是调和p方凹函数时同理得证.

令g(x)=[f(x-1/p)]-p,由定理1知g(x)为[b-p,a-p]上的凹函数,利用凹函数的Jensen不等式,得

代换，即得结果

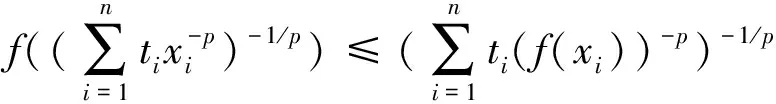
定理6中Jensen不等式还有另一种一般加权形式的表示.

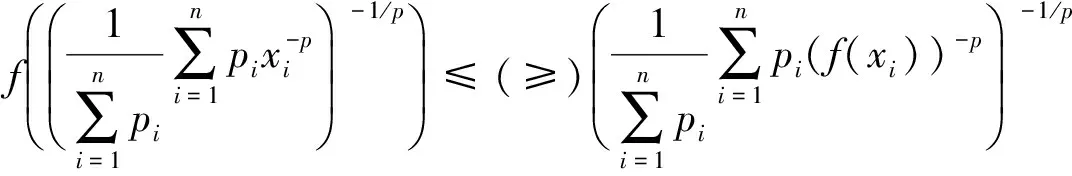
推论1′ (积分型Jensen不等式的一般加权形式) 设φ(x),w(x)是区间[a,b]上的正值连续函数,f(x)是φ([a,b])上连续、正值的调和p方凸(凹)函数,则

证明参照文献[7-8],利用定积分的定义即可证明推论1′.

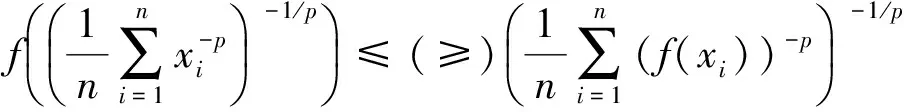
推论2′ (积分型Jensen不等式) 设φ(x)是定义在[a,b]⊂(0,+∞)上的正值连续函数，f(x)是φ([a,b])上正值、连续的调和p方凸函数，则

证明在推论1′中令p(x)=1即得证.

4 调和p次幂s-凸函数Jensen型不等式

证明用数学归纳法可得证明.

5 小 结

给出了调和p方凸(凹)函数与调和p次幂s-凸(凹)函数的定义及其判定定理,建立了调和p方凸函数的离散型和积分型的Jensen不等式,建立了调和p次幂s-凸(凹)函数的离散型Jensen不等式,丰富了凸分析的内容.

[1] 张小明.几何凸函数的几个定理及其应用[J].首都师范大学学报：自然科学版,2004,25(2):11-13.

[2] 宋振云.P方凸函数的性质及Hadamard不等式[J].阜阳师范学院学报：自然科学版,2010,27(4):20-24.

[3] 施未来,时统业,陆敏.与P方凸函数有关的单调函数[J].江苏教育学院学报：自然科学版,2010,27(5):29-30.

[4] 吴善和.调和凸函数与琴生不等式[J].四川师范大学学报：自然科学版,2004，27(4):382-386.

[5] 宋振云,陈少元,胡付高.r次幂平均s-凸函数及其Jensen型不等式[J].东北师大学报：自然科学版,2016,48(4):19-24.

[6]HudzikH,MaligrandaL.Someremarksons-convexfunction[J].AequationsMathematicae,1994,48(1):100-111.

[7] 宋振云. 关于调和凸函数的积分型Jensen不等式[J].湖北技术职业学院学报,2012,15(1):101-104.

[8] 黄大荣,李志艳. 关于Jensen不等式的几个推广[J].甘肃教育学院学报：自然科学版,2000,14(增刊2):4-7.

Abstract：In the report, the harmonic powerp-convex functions and the harmonicp-th powers-convex functions were proposed, and the Jensen inequalities for the harmonic powerp-convex functions and the harmonicp-th powers-convex functions were established.

Keywords：convex function; harmonic powerp-convex function; harmonicp-th powers-convex function; Jensen inequality

HarmonicPowerp-ConvexFunctionandHarmonicp-thPowerMeans-ConvexFunctionandItsCriterions

Shen Jun

(School of Mathematics and Statistics, Hainan Normal University, Haikou 571158, China)

O 17

A DOl：10.15886/j.cnki.hdxbzkb.2017.0033

2017-04-05

海南省自然科学基金(117123)

沈君(1979-)，女，河北保定人，副教授，硕士，研究方向：不确定信息处理、高等数学，E-mail:407519785@qq.com

1004-1729(2017)03-0201-04