鳖臑定义探究
安徽省教育科学研究院 胡 涛 (邮编:230061)
初 数研 究
鳖臑定义探究
安徽省教育科学研究院 胡 涛 (邮编:230061)
“堑堵”、“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓,它们的形状特征如何,古代没有借助线面之间的位置关系对其进行定义,而是从其形成过程予以说明的.
《九章算术·商功》:“斜解立方,得两堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”其意思是说:把长方体沿对角面切开,得到的两个三棱柱,称为堑堵,再沿堑堵的一个顶点和相对的棱将其剖开,得一个四棱锥和一个三棱锥,分别称为阳马和鳖臑,它们的体积之比为2∶1(如图1).

图1
由此解释可知,阳马是底面为矩形,且有一条侧棱与底面垂直的四棱锥.如底面为直角三角形,还有一条不经过底面直角顶点的棱垂直底面,则这样的三棱锥是鳖臑(如图2),诚如刘徽所注:中破阳马,得两鳖臑.
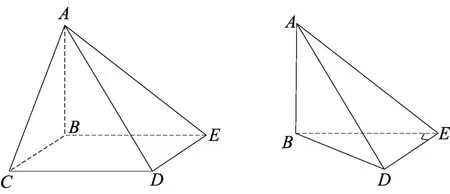
图2
但在《九章算术》又是这样定义鳖臑的:四面都是直角三角形的三棱锥.因此,不免让我们对这两种说法对应的几何体形状是否一致产生疑问.
下面先就此问题展开探究:
记p为:三棱锥的底面为直角三角形,且有一条不经过底面直角三角形的直角顶点的棱垂直于底面.
q为:三棱锥的四面都是直角三角形.
下面证明:p⇔q
1.先证p⇒q

图3
如图3,设三棱锥ABCD的底面是直角三角形,
则BD⊥CD,AB⊥平面BCD,易证AB⊥BD,AB⊥BC,CD⊥AC,
故三棱锥A-BCD的四面都为直角三角形.
2.再证q⇒p
引理1若一个三棱锥的四面都是直角三角形,则不存在这样的顶点,它同时是三个直角三角形的直角顶点.
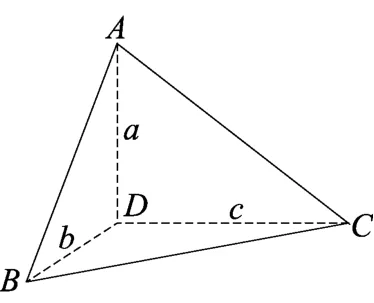
图4
证明如图4,已知三棱锥A-BCD的四面都是直角三角形.
假设存在这样的顶点,它同时是三个直角三角形的直角顶点.不妨设为点D,则有AD⊥BD,AD⊥CD,BD⊥CD.令AD=a,BD=b,CD=c,则AB2=a2+b2,BC2=b2+c2,AC2=c2+a2.
由于
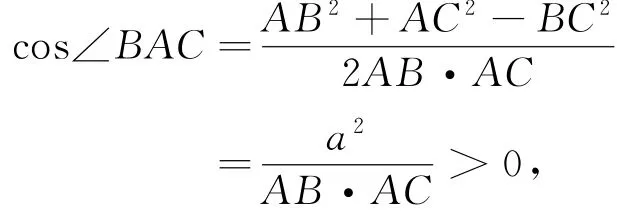
所以∠BAC为锐角.
同理∠ABC,∠ACB均为锐角,则△ABC为锐角三角形.
这与已知矛盾,假设不成立,故命题得证.
引理2若一个三棱锥的四面都是直角三角形,则这四个直角不可能恰好分别在四个顶点处.

图5
为方便讨论,如图5,将三棱锥A-BCD的四个面ABD、ACD、ABC、BCD 分别标记为①、②、③、④,顶点为A的两条棱在面①中的夹角记为A1(即∠BAD),0表示相关的平面角不存在,相应于顶点B、C、D的平面角的记法类似.则三棱锥A-BCD中,相交两棱的夹角在四个面上的分布情况如下:

若其四个直角恰好分别在四个顶点处,不妨设顶点为A的直角在面①中,由于同一面上不能有两个直角,所以只有下面的3种情况:

对于情形1,如图6,四个直角分别为 A1、C2、B3、D4,设AB=a,BC=b,BD=c,CD=a1,AD=b1,AC=c1,则有

图6

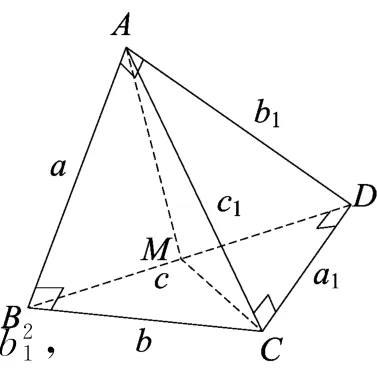
图7
对于情形(2),如图7,四个直角分别为 A1、D2、B3、C4,设AB=a,BC=b,BD=c,CD=a1,AD=b1,AC=c1,则

可知a=a1,b=b1,c=c1.
所以这种情形也不可能.
对于情形(3):证明同情形1.
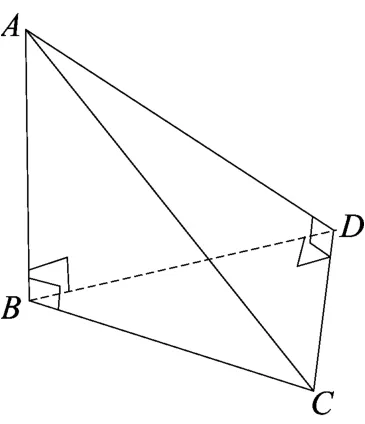
图8
综上 ,引理2得证.
由引理1、2知,若三棱锥A-BCD的四个面都是直角三角形,则一定存在一个顶点,它是两个直角三角形的直角顶点,
不妨设为点B,在该处的2个直角为B1、B3,即∠ABD=∠ABC=90°,则AB⊥平面BCD.
综合1、2,我们证明了p⇔q.
在上面的证明过程中我们还得到了四个直角在三棱锥A-BCD上分布的情况:在两个顶点上,且每个顶点处各有两个(如图8).
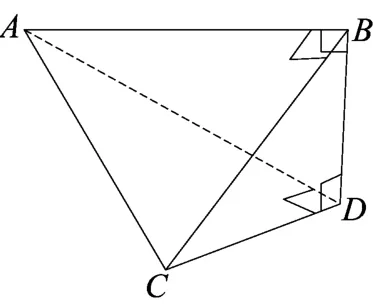
图9
至此可看出在《九章算术》中,实际上已给出了鳖臑这种特殊几何体的两种不同定义方式.当然鳖臑还可以从其他角度对其进行定义,如:若三棱锥中存在三条棱,其中两条互相垂
直,另一条是这两条棱的公垂线段,则称这个三棱锥为鳖臑.这三条棱就是图9中的棱CD、AB、BD,三棱锥的4个顶点都在其上,也就是《九章算术》所指的鳖臑下广,上袤和高,它们的长度决定了鳖臑的体积.
比较鳖臑的几种定义,表述最为简洁的显然是:四面都是直角三角形的三棱锥.笔者推测也许是感觉到这种定义不便于人们快速把握鳖臑的构成要素间的位置关系,《九章算术》才又借其形成过程加以解释,以便判定.果真如此,更显示出我国古代数学家的智慧和研究水平.
1 张苍,九章算术[M].南京:江苏人民出版社,2011
2 何文忠,立体几何体中的一个重要基本图形-鳖臑[J].数学通报,1996(5)
3 沈康身,鳖臑与合盖[J].自然杂志,1989(8)
2017-06-20)
——《认识直角》教学片断与解读

