落实素养 注重“四基” 保持特色——2017年安徽中考数学试卷评析及教学建议

安徽省合肥市海顿学校 刘昌福 时亚男 (邮编:638400)

复 习考 试

落实素养 注重“四基” 保持特色
——2017年安徽中考数学试卷评析及教学建议

安徽省合肥市海顿学校 刘昌福 时亚男 (邮编:638400)

随着2017年中考帷幕落下,各地中考数学试卷款款而至,其中安徽省中考数学试卷仍以她独特风姿,展示在我们面前．从题面上看,“似曾相识”却又“耳目一新”．试题梯度合理,考查了不同层次学生的数学能力．再深入研究,可以发现,试题既注重考查基础知识、基本技能,又关注基本的数学思想方法和基本的数学活动经验(俗称“四基”)．坚持这样考查,的确对落实学生“学会学习”“科学精神”“实践创新”等方面的基本素养,大有益处．这些基本素养的提高,必定为学生的全面发展、终身发展奠定基础．

下面结合今年合肥市阅卷情况,对中考数学试卷和学生的答题情况进行分析,并谈一谈对今后的数学教学方面若干粗浅的建议,仅供参考．

1 试卷的总体情况分析

安徽中考数学试卷一直坚持稳定第一、特点鲜明、突出能力、着意创新等独有特色,以下仅从四个方面加以分析．

1．1 试卷结构稳定

试卷共23题,总分150分．设置选择题、填空题和解答题三种题型．其中选择题10题(计40分),填空题5题(计20分),解答题8题(计90分),保持了中考命题硬件方面的稳定性．

1．2 考点分布稳定

从考题涉及内容看,与《义务教育数学课程标准》(2011)(以下简称《课标》)要求完全一致,涵盖了《2017年安徽省初中毕业学业考试纲要》(以下简称《考纲》)中的大部分核心考点,这样的考点分布促进教师研读《课标》和《考纲》,提高课堂效率．

表1 试卷考查的知识点分布

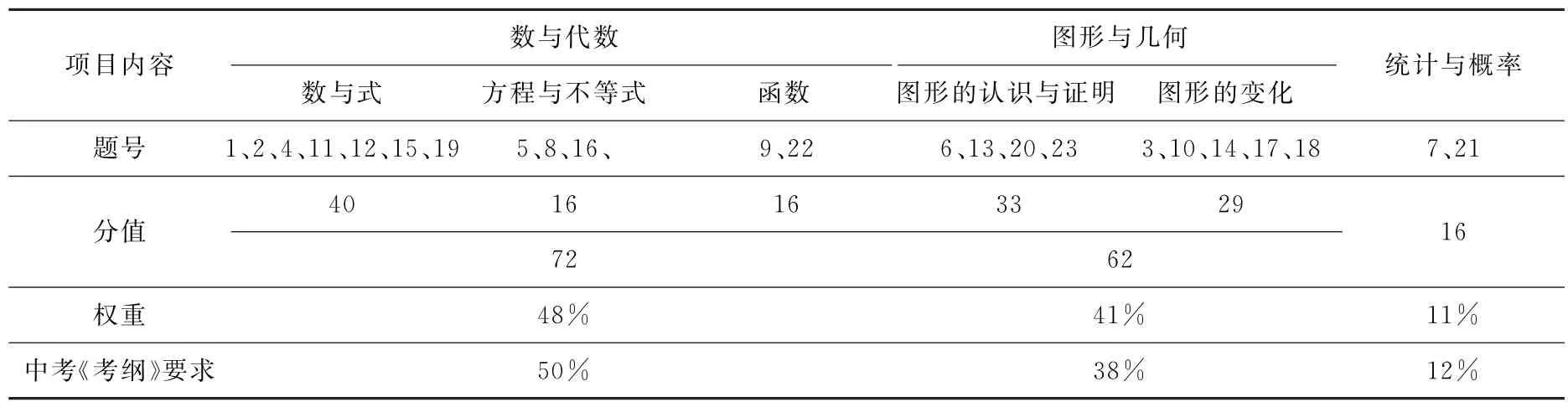
表2 试卷考查的知识点分布

1．3 试题难度稳定

试题结构遵循由易到难原则,每种题型的最后一题设置成“压轴”题,层次分明．本卷除第9、10、14、22、23题有难度或难度较大外,其它试题都较易入手．这样既保证了全体学生的基本分数,同时也为数学能力较强的学生提供了展示的舞台．这也是这份试卷所必须保持的两大功能,既要保证全体学生初中毕业这个全体性,又要兼顾甄别选拔优秀分子进入高中学习这个选拔功能．2017年合肥市区参加中考人数为29484人,根据阅卷情况,了解合肥市区2017年中考数学试卷得分情况统计如下:

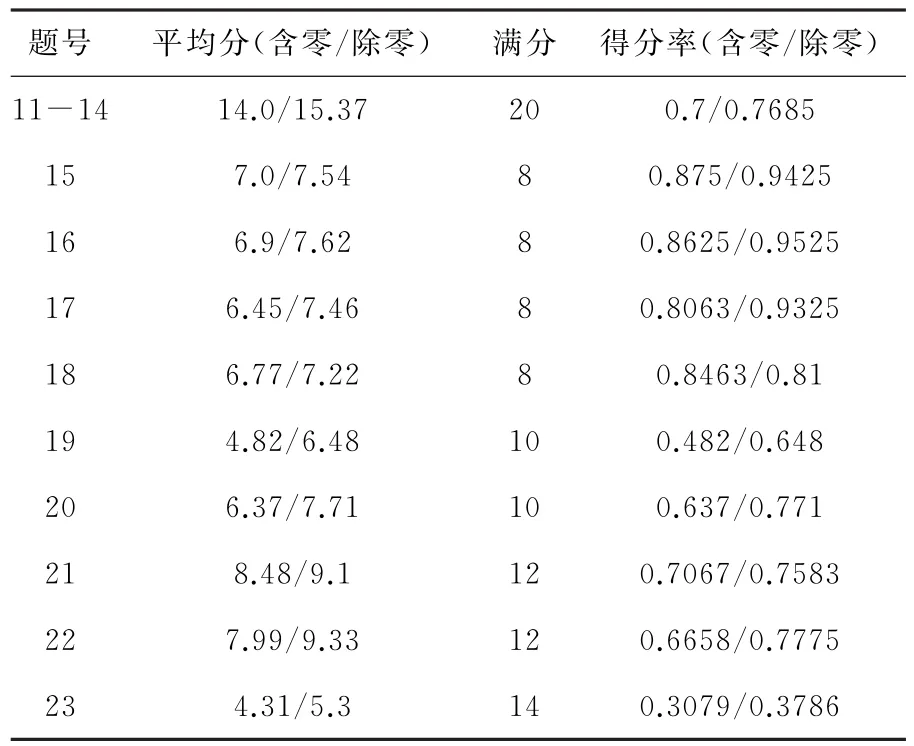
表3

1．4 试题特点鲜明

安徽省中考数学试卷一直以她独有的鲜明特点领先潮流,以下仅掬几多浪花以飨读者．

特点一与时俱进,渗透中国元素

2017年中考数学试卷不仅考查数学知识,同时渗透当前的政治经济热点话题和中国传统文化元素．如第4题以 “一带一路”为情境,第7、8题分别以学生社团活动和药品降价为背景,尤其是第16题引用《九章算术》中“盈不足术”问题,使得学生在学习数学知识的同时了解社会实际、感受中国传统文化的博大精深和我国数学研究的悠久历史,在弘扬中华文化的同时,增强民族自豪感．

特点二以人为本,关注全体学生

本卷中的三大题型:选择题、填空题和解答题,都是由易到难,从方便学生入手,在保护学生答题信心方面给予较多关怀．如选择题的第1－8题,填空题的第11－13题,解答题的第15－18题,都是基础题,让学生得到基本分,同时增强考试信心,体现关爱学生,以人为本的理念．即使第23题这个压轴题的前两个问题,也比较容易,仍然体现了以上所说．坚持这样的考查方式,的确能保证“人人获得有价值的数学”．

特点三考查“双基”,兼顾“思想”“经验”

自新课改以来,安徽省中考数学试卷坚持稳定第一．稳定,不仅体现在时间、题型、分值等硬件方面,很多基础知识、基本技能的考查也相当稳定,这就是我们俗称的高频考点．今年也不例外(详见试卷考查的知识点分布表1),有的考点甚至多次出现．这个特点说明:考查“双基”(基础知识、基本技能),永不过时．在考查“双基”的同时,兼顾基本数学思想方法和基本数学活动经验的考查．如第14题的分类思想、第19题的数形结合思想、第23题的探究线段中点的数学活动经验的应用等．

特点四突出重点,考查数学经典

多年来,安徽省中考数学试卷一直在初中数学的重点知识、经典方法上不断挖掘．今年也有多处体现．如第17题中的“化斜为直(正)”,第8题、16题和第22题的建立方程模型或函数模型解决实际问题,第23题的借助线段中点构造全等三角形和几何运算等,蕴含其中的都是初中数学的经典,这些数学经典对提升学生的数学素养很有帮助．

特点五“理”中有“文”,重视阅读理解

很多人狭义地理解数学就是计算、证明,其实解决数学问题一定是以通过阅读对问题的准确理解为前提．正所谓“读题三遍,题意自见”．如第16题和第19题就是一个很好的说明．只有认真阅读,才能真正理解题意,否则就不可能准确地解答问题．尤其是第19题,之所以得分率较低(合肥市得分率0．482),就反映出我们平时的数学教学在这方面存在的问题,这必须引起我们足够的重视．要知道我们的科学巨匠们,他们几乎个个都是文史功底极高的人,你读读钱学森、华罗庚、苏步青等大师们的著作,就一定会颠覆“数学与人文底蕴无关”这个观点．

特点六实践操作,动手学习数学

本试卷在考查动手实践操作方面,着墨较浓,如第14、18、19题都有涉及．这也是安徽省中考数学试卷一直保持的一大亮点．我们在数学教学中,一定要让学生感受到:计算、证明是学习数学的重要方法,实践操作也是学数学的好手段．先实践操作(如画图、测量、折叠、剪拼、平移、旋转等),获取基本数学活动经验,找到有效的解决问题的思路,就能使很多数学问题迎刃而解．

特点七稳定为基,坚持不断创新

坚持试卷各方面的稳定,始终是主旋律,但在建设创新型国家的大环境下,着意创新,也必须体现．创新,本来就艰难,在万众瞩目下创新,更是难上加难．但今年的中考数学试题还是在这种艰难的环境下迈开创新步伐．如第14题一改多年的多项选择为分类讨论,又打开了一条命题新思路．同时,笔者还以为,数学试卷中增加文史元素,也契合中高考的改革思路,这其实在为培养复合型人才奠基．

2 试题赏析

今年中考数学试卷中的23道试题,题题精心命制,亮点遍布试卷,以下仅对今年少有出现的几道中考好题进行浅析,供大家欣赏．

例1(第9题)已知抛物线y＝ax2＋bx＋c与反比例函数的图象在第一象限有一个公共点,其横坐标为1,则一次函数y＝bx＋ac的图象可能是( )

赏析本题考查一次函数、二次函数和反比例函数的图象与性质．由二次函数图象与反比例函数图象在第一象限有一个公共点,可求出公共点坐标为(1,b),且b＞0;根据公共点的意义,把(1,b)带入二次函数y＝ax2＋bx＋c中,可得a＋c＝0,即a与c互为相反数,所以ac＜0,最后根据一次函数的性质得出答案B．当然,本题可以用排除法先排除C、D选项,从而提高正确率．

本题综合考查一次函数、二次函数和反比例函数的图象与性质,将初中阶段所学的函数知识集于一题,可见命题者是煞费苦心的．同时也对学生全面掌握初等函数知识提出更高要求,题目难度不大,但综合性强,作为选择题的次压轴,恰到好处．

例2(第10题)如图,矩形ABCD中,AB＝5,AD＝3．动点P满足S△PAB＝S矩形ABCD．则点P到A、B两点距离之和PA＋PB的最小值为( )

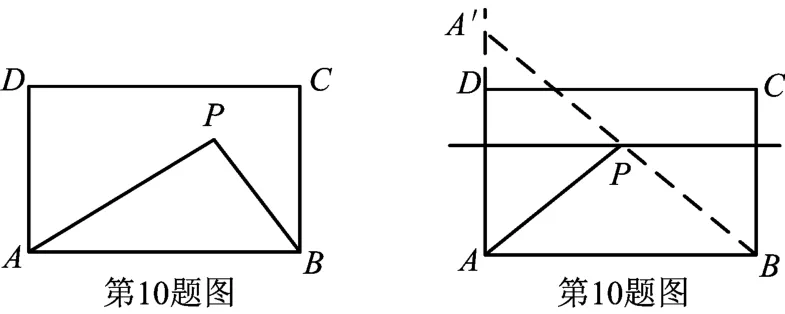
赏析本题考查由轴对称性求两线段之和的最小值,对于这个模型学生大都较为熟悉,可谓“有法可依”．根据条件S△PAB＝S矩形ABCD可得点P在与AB平行且到AB距离为2的直线上,则问题转化为在此直线上找一点P,使点P到A、B两点距离之和最小．学生需动手操作,根据轴对称性找到点A关于直线的对称点A′,连接A′B,A′B与直线的交点即为使PA＋PB最小的点P的位置,最小值即为线段A′B的长．在Rt△A′AB中,A′A＝4,AB＝5,由勾股定理得A′B＝,即答案为D．

本题考查点的轨迹问题,体现了初高中的知识衔接．同时,动手与动脑相结合．美中不足的是:答案中的P点恰巧为线段A′B的中点,就会导致学生即使不知道由轴对称性求线段之和的最小值这个模型,而根据特殊位置的点(线段A′B的中点)也能猜出答案,从而影响试题的信度．

例3(第14题)在三角形纸片ABC中,∠A＝90°,∠C＝30°,AC＝30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为________cm．

赏析本题涉及轴对称、三角形全等、等腰三角形、解直角三角形和勾股定理等几何知识．

通过折叠、裁剪获取基本数学活动经验可得这个“某点”可以是点E、D(如图),但不可能是点B,根据轴对称性易证展开后的平行四边形为菱形．所以,通过解直角三角形得菱形边长分别为10cm、53cm,故答案是40cm或203cm．

本题新颖有趣,动手操作是前提,获取基本数学活动经验是关键,而利用几何知识计算是本质．同时考查分类讨论、数形结合等基本数学思想,题目形式上也有创新．作为填空题的压轴题,在计算不复杂的前提下,综合考查学生的“四基”以及动手操作和空间想象能力,如此全面体现,着实让人拍案叫绝．

例4(第20题)如图,在四边形ABCD中,AD＝BC,∠B＝∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE．

(1)求证:四边形AECD为平行四边形;

(2)连接CO,求证:CO平分∠BCE．

赏析本题考查圆的性质、平行四边形的判定和性质,以及角平分线的判定等知识．第(1)题方法较多．从学生答题情况可发现以下两种方法较为典型:①由平行四边形定义可证．因为CE∥AD,再证CE∥AD即可．根据圆周角的性质得∠B＝∠E,所以∠D＝∠E,从而∠D＋∠DAE＝180°,所以AE∥CD,即四边形AECD为平行四边形;②由平行四边形判定定理可证．易证△DAC≌△ECA(AAS),所以CE＝AD,又CE∥AD,即四边形AECD为平行四边形．第(2)题在第(1)题的前提下设问．要证CO平分∠BCE,由定理“到角的两边距离相等的点在这个角的平分线上”,可得辅助线:作OM⊥EC于M,ON⊥BC于N．此时的OM、ON为弦心距,因为EC＝BC,所以OM＝ON,即CO平分∠BCE．

从学生答题情况看,解法还有很多,如延长CO,得圆的直径CP,连接EP、BP所以∠CEP＝∠CBP,易证△CEP≌△CBP(HL),所以∠ECO＝∠BCO,所以CO平分∠BCE．其他方法不再赘述．

此题综合考查圆的有关知识,难度适中,坡度平缓,完全与《课标》、《考纲》要求吻合,又解法多样,有利于学生解答,又是一道好题．

例5(第23题)已知正方形ABCD,点M为边AB的中点．

(1)如图1,点G为线段CM上的一点,且∠AGB＝90°,延长AG、BG分别与边BC、CD交于点E、F．

①求证:BE＝CF;

②求证:BE2＝BC·CE．

(2)如图2,在边BC上取一点E,满足BE2＝BC·CE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值．

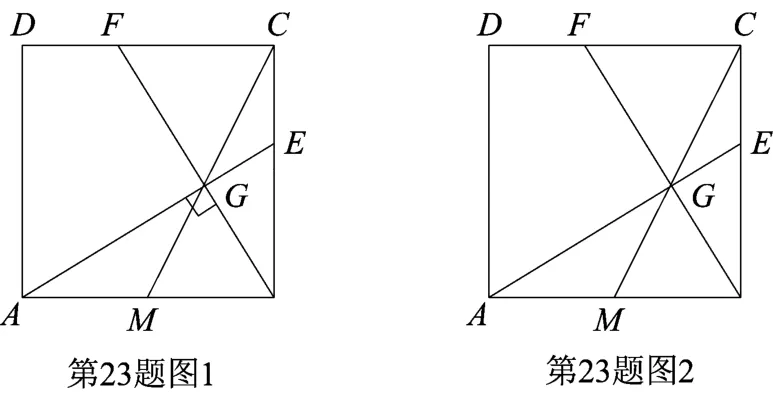
赏析本题是这份试卷的最后一题,主要考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、余角的性质、对顶角相等、直角三角形斜边中线的性质、等腰三角形的判定和性质等知识点．

第(1)题学生比较熟悉．①求证:BE＝CF;绝大多数同学能够结合正方形性质联想到用全等三角形知识解决．②求证:BE2＝BC·CE．分析思路为:BE2＝BC·CE⇐ △CEG∽△CBG⇐ ∠CGE＝∠CBG⇐CG＝CF．由∠AGB＝90°,且点M为边AB的中点,可得CG＝CF．从而问题解决．

第(2)题,从阅卷情况看,学生的解题方法很多,如几何计算、构造法、同一法、解析法等,这里仅给出使用几何计算的解题方法,具体如下:

因为BE2＝BC·CE,所以CF＝BE．

设正方形边长为2x,则AM＝BM＝x,因为BE2＝BC·CE,解得BE＝ 5－1( )x＝CF,所以

本题将直角三角形斜边上的高、“X型相似三角形”等基本图形融合在一起,构思巧妙,特点鲜明．同时,试题设计多题把关,既有同一条件下的层层递进,又有独立设问,对学生分析问题、解决问题的能力的考查非常到位．同时解决的思路较为广泛和经典,如利用线段中点构造全等三角形和通过几何运算解决几何问题等都是数学的经典内容．

3 教学建议

毛主席说:“在战争中学习战争”．我们也应该从考试中学会指导学生考试．我们总结考试的规律和特点,分析学生答题思路和存在的问题,就是为以后的课堂教学找到正确的道路,从而提高教与学的效率．以下为笔者不成熟的若干建议．

3．1 落实核心素养,着眼学生未来

2016年9月,国家教育部提出中国学生发展核心素养,综合表现为六个方面:人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新．从今年的中考数学试题看,我们的数学课堂不仅要成为科学精神、学会学习、实践创新这三方面的主战场,在其它三个方面也要有所担当．只有这样,才能使学生一直保持学习数学的兴趣,使学生充满无限的发展潜力,这正是为学生全面发展和终身发展考虑．

3．2 落实“四基”、“四能”,提升数学素养

《课标》上提出夯实学生的基础知识、基本技能、基本数学思想、基本数学活动经验(俗称“四基”),同时又提出提高学生发现问题的能力、提出问题的能力、分析问题的能力、解决问题的能力(俗称“四能”)．安徽省中考数学试题一直坚决贯彻落实．对于“双基”(基础知识、基本技能),我们的教学都能扎实贯彻到位,对于基本的数学思想、基本的数学活动经验我们也应同时落实．同样,我们的数学教学在提高“双能”(分析问题的能力、解决问题的能力)上做得不错,但也要落实在提高学生发现问题、提出问题的能力上．只有这样,才能真正地提升学生的数学素养,全面发展学生的数学能力．

3．3 立足平时教学,做到水到渠成

多年的经验教训告诉我们,要想学生考出好成绩,绝不是靠一份资料、几套试卷能实现的．必须依赖我们三年扎扎实实的课堂教学．挤干每一节课的水分,提高每一节课的效率,才是教学正道．因为,只有在平时的每节新授课的教学中,我们才能完整地让学生经历知识产生的过程,像科学家般地自己寻找解决问题的方法和路径(复习课往往难以实现)．而这些才是真正考试所需要的．有了扎扎实实的每一节新授课,学生的数学能力自然就会提高,其实分数就成了副产品．

3．4 研读《课标》、《考纲》,提高复习效率

在有了高效的新授课教学的前提下,在有限的复习时间里(一般只有100天),提高复习课的效率,又是提高学生成绩的另一大法宝．而提高复习课效率的前提就是要正确研读《课标》、《考纲》,正确把握复习方向．在此有个建议,《课标》、《考纲》一定要成为我们上好复习课的工具书,绝不能只依照某份复习资料去上复习课,那一定是本末倒置．说到正确研读《课标》、《考纲》,我仅举一例供参考．例如概念教学,在新授课中,重要无比．比如函数的概念,我们在新授课教学中,一定会挖空心思,引导学生理解函数的概念,但在《考纲》中,函数的概念只是A档要求,因此到了复习课阶段,大多的概念已经不是我们的课堂重点．通过这个小例,你就会真正理解《考纲》中将知识点划分为A、B、C、D四个档次的要求的真正用意．因篇幅关系,不再赘述．

3．5 老师入题海,学生驾轻舟

数学试题浩瀚如海,学生不可能穷尽试题．同时中考试题又绝不考陈题、旧题,因此题海战术对学生一定是低效率的,只能徒增学生的学习负担．那种想通过不断刷题,从而碰巧遇到中考题的想法只能是妄想．因此我们的建议是老师必须广猎试题,总结方法和规律,这就是教师入题海．只有老师多见题型,在教学中才能对试题进行变式和拓展,从而提高复习课效率．而通过老师的引导启发,学生也会通过解答有限的一些典型试题,自己悟出一些方法和规律,这就是学生驾轻舟．

2017-07-29)