一类以“拐点”为背景的函数试题解法及思考

湖北省武汉市黄陂区第一中学盘龙校区 李红春 (邮编:430312)

一类以“拐点”为背景的函数试题解法及思考

湖北省武汉市黄陂区第一中学盘龙校区 李红春 (邮编:430312)

函数是高中数学的核心内容,以高等数学知识为背景的函数题,因其背景公平,能考查学生临场应变能力,和后继学习的能力,倍受命题者的青睐．通过研究发现,以高等数学中的“拐点”知识为背景的试题正悄然升温,值得关注．

1 “拐点”的概念

拐点,又称“反曲点”,是函数图象凸凹的分界点,是函数的一阶导函数单调性发生改变的点,直观地说,就是使切线穿越曲线的点．对于可导的函数f(x)而言,若其在拐点处有二阶导数,则二阶导数为零,且二阶导数在拐点附近两侧异号．比如:顺着x轴的正方向看,在x＝0附近,f(x)＝x3图象从上凸变为下凸,函数f(x)＝sinx的图象从下凸变为上凸,所以零是它们的拐点．有些函数可能没有拐点,如二次函数,有些函数只有一个拐点如f(x)＝x3,而有些可能有多个,如f(x)＝sinx．

2 应用

考点1拐点处的切线“穿越”曲线

例1已知函数f(x)的图象在点(x0,f(x0))处的切线的方程为l:y＝g(x),若函数f(x)满足∀x∈I(其中I为函数f(x)的定义域),当x≠x0时,(f(x)－g(x))(x－x0)＜0恒成立,则称x0为函数f(x)的“分界点”,已知函数f(x)满足则函数f(x)分界点的个数为______．

解法1,故可设f(x)＝6x－x2－4lnx－c,由f(1)＝5,得c＝0,即f(x)＝6x－x2－4lnx,(f(x)－g(x))(x－x0)＜0⇔当x∈(0,x0)时,f(x)－g(x)＞0;当x∈(x0,＋∞)时,f(x)－g(x)＜0;依题意得,

故h(x)＝f(x)－g(x)＝6x－x2－4lnx－,则令得．故当x0＝2时,对∀x∈(0,＋∞),都有h′(x)＜0,函数h(x)为减函数,而h(x0)＝0,则对任意x∈(0,x0),h(x)＞h(x0)＝0,即f(x)－g(x)＞0;当x∈ (x0,＋∞)时,h(x)＜h(x0)＝0,即f(x)－g(x)＜0;所以x0＝ 2是“分界点”．当x0＞ 2时,对任意x∈),h′(x)＜0,h(x)为减函数,当x∈时,h′(x)＞0,h(x)递增,则存在m使得h(m)＜h(x0)＝0,这与“分界点”的要求矛盾．同理,当0＜x0＜ 2时,也不符合题意．

故“分界点”的个数只有一个．

解法2f′(x)＝6－故可设f(x)＝6x－x2－4lnx－c,由f(1)＝5,得c＝0,即f(x)＝6x－x2－4lnx,x∈ (0,＋∞),于是f″(x),令f″(x)＝0,得又f″(x)在两侧异号,故是图象的拐点,亦即是题目中的“分界”点．

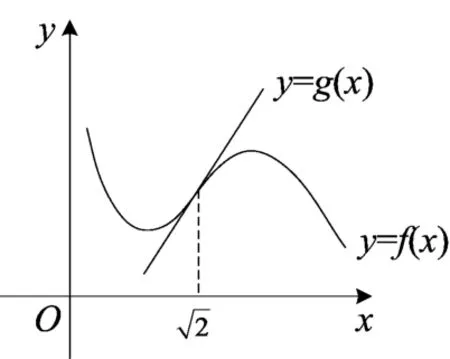
图1

点评本题是一个新定义型试题,本质上是高等数学中的“拐点”用简单明了的初等数学式子进行包装,相对于解法1的繁琐,解法2从本质出发,即切线在切点处“穿越”了曲线,且切点两侧不再有交点．如图1所示,当时,f″(x)＞0,f′(x)递增,即曲线的切线斜率由小变大;当时,f″(x)＜0,f′(x)递减,即曲线的切线斜率由大变小．可见曲线的切线在横坐标x＝2的切点处“穿越”了曲线,且除了切点再无其他交点,2就是函数f(x)的拐点．

考点2拐点与对称中心

例2(湖北省2016届八校联考题)已知直线x－9y－8＝0与曲线C:y＝x3－px2＋3x相交于A、B,且曲线在A、B处的切线平行,则实数p的值为( )

A．4 B．4或－3

C．－3或－1 D．－3

解法1由y＝x3－px2＋3x,得:y′＝3x2－2px＋3,设A(x1,y1),B(x2,y2),则曲线C在点A、B处的切线斜率分别为,令＋3＝m,则x1、x2是方程3x2－2px＋3－m＝0的两个根,则,一方面

当p＝－1时,曲线C:y＝x3＋x2＋3x,y′,曲线C与直线x－9y－8＝0只有一个交点,舍去．

故p＝4或－3．

解法2y′＝3x2－2px＋3x,y″＝6x－2p,由y″＝0得则,于是曲线C的对称中心为

将对称中心代入直线x－9y－8＝0,得p3－13p－12＝0,解之得:p＝－1,－3或4,后略．

点评作为一道选择题,解法1计算量大,变形较为复杂,是典型的“小题大做”;解法2由题意出发,分析出直线必过三次函数的对称中心后,先借助二阶导数,求出函数f(x)的对称中心,再代入直线方程求解,解答简洁明了,应该是命题者的初衷．事实上,三次函数的拐点就是其对称中心的横坐标．

2．3考点3拐点偏移

一般地,对于可导函数f(x),若x＝n是其拐点,那么:①当函数f(x)的图象在点(n ,f(n))两侧(两侧附近)的图象具有中心对称性时,拐点即是函数图象(或局部图象)的对称中心,这时若f(x1)＋f(x2)＝2f(n),则x1＋x2＝2n;②若函数f(x)的图象在点(n ,f(n))两侧(两侧附近)的图象不具有中心对称性时,我们形象的称之为拐点发生了“偏移”,这时若f(x1)＋f(x2)＝2f(n),则x1＋x2≠2n,具体说,当x1＋x2＞2n,则拐点左偏;当x1＋x2＜2n,则拐点右偏．

例3(武钢三中2017届高三训练题)已知函数f′(x)为f(x)的导函数,设A(x1,f(x1)),B(x2,f(x2))是函数f(x)图象上不同的两点,且满足f(x1)＋f(x2)＝0,求证

证明≥0,即f(x)在(0,＋∞)内递增,不妨设x1＜x2,注意到结合函数的单调性知:,要证而f(x1)＋f(x2)＝0,即只需证

例4(黄陂一中2017届高三周练题)已知函数f(x)＝2lnx＋x2＋x,若正实数x1、x2满足f(x1)＋f(x2)＝4,求证:x1＋x2≥2．

证明,故f(x)在(0,＋∞)内递增,不妨设x1≤x2,由f(1)＝2知,x1≤1,x2≥1,要证x1＋x2≥2⇔x1≥2－x2⇔f(x1)≥f(2－x2)⇔4－f(x2)≥f(2－x2)⇔f(x2)＋f(2－x2)≤4．设F(x)＝f(x)＋f(2－x),x≥1,则

即F′(x)≤0,故F(x)在 [1 ,＋∞)内递减,于是F(x)≤F(1)＝2f(1)＝2×2＝4．

点评以上两道试题都是已知f(x1)与f(x2)的关系,证明与x1、x2有关的不等式,若从条件中的双变量函数方程出发,要用x1、x2中的一个量表示另一个量很难,于是从结论着手,采用分析法,借助函数f(x)的单调性,将待证的不等式不断等价转化,最终归结为只含有x1或x2的不等式,最后通过构造函数,借助单调性解决问题．

本质上讲,极值点偏移刻画的是函数图象的“轴对称”形态,而拐点偏移刻画的是函数图象的“中心对称”形态．从近年来,“极值点偏移”问题已经连续多次出现在高考试卷中,如2010年天津卷、2011年辽宁卷、2013年辽宁卷、2016年全国乙卷等,高考命题讲究传承与创新,所以笔者认为:“拐点偏移”问题极有可能成为下一轮高考命题的新热点,值得关注!

2017-07-05)