配筋对混凝土徐变的影响分析
曹国辉,阳亮,张锴,彭细荣
配筋对混凝土徐变的影响分析
曹国辉1,阳亮2,张锴1,彭细荣1
(1. 湖南城市学院土木工程学院,湖南益阳,413000;2. 湖南大学土木工程学院,湖南长沙,410082)
基于龄期调整的有效模量法和内力重分布机理,引入钢筋修正系数预测钢筋混凝土的徐变并且推导出相应的计算公式。通过对相关数据进行拟合分析,验证钢筋修正系数的有效性和实用性。在此基础上,提出基于现行公路桥涵设计规范徐变模型的配筋混凝土徐变计算公式,并分析老化系数、配筋率、加载龄期等参数对徐变的影响。研究结果表明:配筋对混凝土徐变具有抑制作用;当配筋率很小时,配筋对混凝土的相对抑制作用最强,随着配筋率增大,相对抑制作用逐渐降低;加载龄期和配筋对混凝土徐变的影响有叠加作用,并且这种叠加作用不只是简单的线性叠加。
钢筋混凝土柱;徐变;钢筋修正系数;基于龄期调整的有效模量法;配筋率
收缩和徐变是混凝土的一种固有特性,引起结构的内力重分布及时变变形,对结构产生不利影响。国内外诸多学者对混凝土的收缩徐变进行了大量的理论与试验研究[1−4],并且在此基础上提出了许多具有一定精度的收缩徐变预测模型,如ACI209模型、CEB-FIP(1990)模型、B3模型、GL2000模型和JTG D62—2004模型等。然而,影响混凝土徐变的因素十分复杂、多样且具有不确定性,使得混凝土收缩徐变规律没有被完全准确掌握,目前还没有一种理论可以准确地预测和解释混凝土的收缩徐变特性[5]。已有的收缩徐变预测模型都是在素混凝土的基础上统计分析得到[6−7]。人们对于钢筋混凝土柱的收缩徐变研究较少,基本都是基于某特定配筋率下的收缩徐变拟合出相应的配筋影响系数。相关研究表明,配筋对混凝土的收缩徐变影响明显,对混凝土的收缩徐变具有约束作用,因此,建立一种考虑配筋修正系数的混凝土收缩徐变预测模型,更加准确地预测混凝土的收缩徐变十分重要,对指导实际工程设计具有重要意义。
1 钢筋混凝土柱长期变形计算方法
在长期荷载作用下,钢筋混凝土柱的计算方法和理论通常有继效流动理论、有效模量法、徐变率法以及按龄期调整的有效模量法等。按龄期调整的有效模量法是计算混凝土收缩徐变导致应力和变形最常用的数值分析方法之一,其计算过程简单,计算结果也较理想。本文作者基于按龄期调整的有效模量法[8]计算钢筋混凝土柱的长期变形。
钢筋混凝土柱在长期荷载作用下由于混凝土的收缩徐变会产生内力重分布,其长期变形由3部分组成,即初始内力作用下混凝土的弹性应变及徐变、内力重分布过程中改变的次内力产生的混凝土瞬时应变和徐变以及混凝土的收缩应变。基于龄期调整的有效模量法可得混凝土长期变形的计算公式如下:
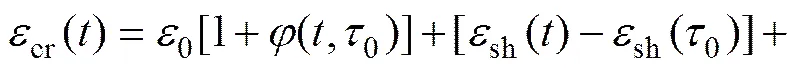
(1)
其中:
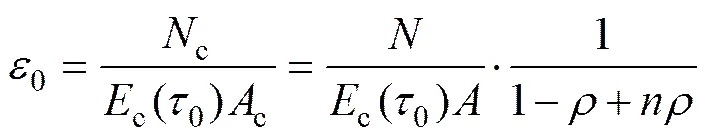
在计算过程中,假定钢筋混凝土柱内力平衡,钢筋和混凝土不发生相对滑移,即满足变形协调条件,则长期荷载作用下钢筋的变形可由下式表示:
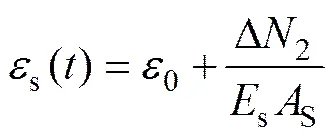
式中:Δ2为钢筋内力变化值。
由变形协调条件知:
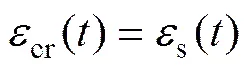
由于钢筋混凝土柱的内力重分布是体系内的一种自平衡,因此,混凝土内力的减少量等于钢筋内力的增加量,即
(5)
将式(1),(2),(3)和(5)代入式(4)可得
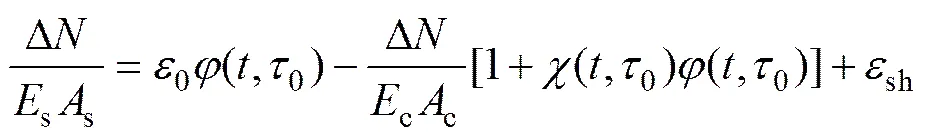
式中:
(6)
由式(6)可解出钢筋混凝土柱内力重分布的次内力为
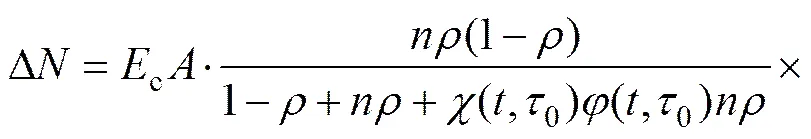
(7)
将式(7)代入式(3),可得
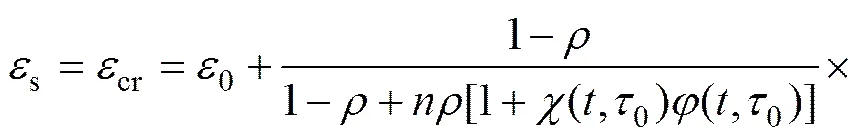
(8)
由混凝土的徐变系数定义可知,徐变系数为徐变应变与瞬时弹性应变之比。式(8)包括瞬时弹性应变、徐变应变和收缩应变,故钢筋混凝土柱的徐变系数可用下式表示:
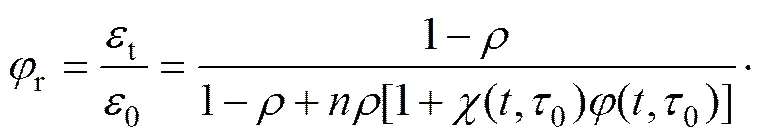
(9)
定义钢筋修正系数为
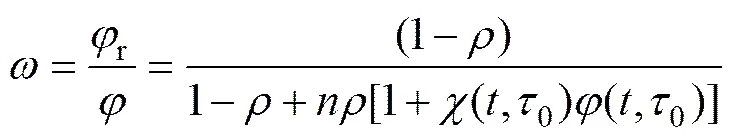
2 混凝土徐变模型的确定
采用JTG D62—2004模型[9]计算混凝土的收缩徐变系数。其计算公式如下:
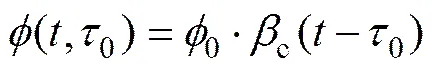
式中各参数的意义及具体计算公式见文献[9]。修正钢筋混凝土柱的徐变计算公式为
(12)
式中:为钢筋修正系数。
3 钢筋修正系数预测精度分析
目前,对钢筋混凝土的徐变研究较少[10−15],收集到的样本数据也很有限。本文通过对文献[11−13]中混凝土徐变数据进行拟合分析,以验证修正模型的适用性及预测收缩徐变的精确性。钢筋修正系数预测结果对比见图1。
从图1可见:混凝土徐变前期增长速度较快,随着时间推移逐渐达到平缓;素混凝土的徐变明显高于钢筋混凝土的徐变,说明配筋对混凝土徐变影响很大,采用钢筋修正系数预测徐变能够很好地考虑配筋对混凝土徐变的抑制作用,预测趋势也与混凝土徐变增长趋势相一致,预测的徐变明显小于素混凝土的徐变,与实际钢筋混凝土的徐变很接近。
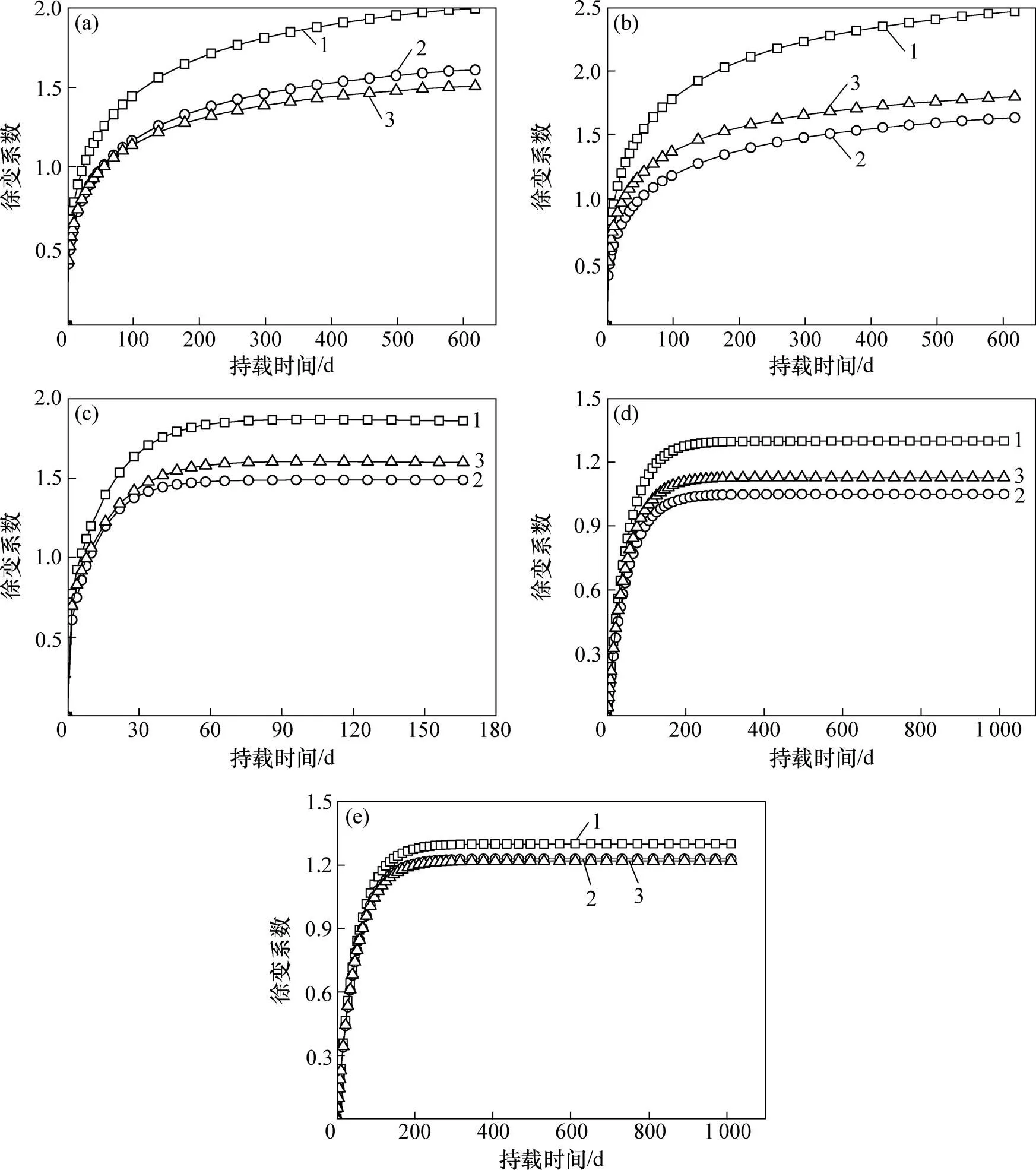
(a) 文献[11]中预测结果对比,t0=7 d,ρ=0.76%;(b) 文献[11]中预测结果对比,t0=9 d,ρ=1.70%;(c) 文献[12]中预测结果对比,t0=21 d,ρ=1.50%;(d) 文献[13]中预测结果对比;t0=7 d,ρ=0.71%;(e) 文献[13]中预测结果对比,t0=39 d,ρ=1.70%
曹国辉等[11]研究了低强钢筋混凝土的徐变特性,并考虑了不同加载龄期的影响。从图1(a)和图1(b)可见:加载龄期对混凝土徐变影响很大;采用钢筋修正系数预测徐变,在加载龄期为9 d时,预测值高于实际值;在加载龄期为39 d时,预测值略低于实际值。张克波等[12]进行了配筋混凝土的徐变试验研究,混凝土强度为C50,基于试验结果给出了钢筋的影响系数。从图1(c)所示的修正结果看,修正值略高于实际值,但差别不大。张运涛等[13]研究了不同配筋率的钢筋混凝土柱的收缩徐变特性。从图1(d)和图1(e)可知:采用钢筋修正系数预测徐变与实际钢筋混凝土徐变均拟合较好;当配筋率很低时,素混凝土徐变与钢筋混凝土徐变差别很小,修正系数的预测结果精度也越高。实际上,当=0时,=1,采用钢筋修正系数所得的徐变即为素混凝土的徐变。
通过对文献[11−13]中混凝土徐变数据进行拟合分析可知,采用钢筋修正系数能够很好地预测钢筋混凝土的徐变,预测值和实际值相差不大。预测结果早期徐变拟合得非常好,随着时间推移产生一些偏差,但差值并不是很大。图1中,采用钢筋修正系数预测的徐变与实际配筋混凝土的徐变终值误差仅在±7%以内,可以认为采用钢筋修正系数可以很好地预测配筋混凝土徐变。张运涛等[13]研究的是配筋高强混凝土的收缩徐变试验,从图1(d)和图1(e)可以看出:钢筋修正系数不仅适用于普通钢筋混凝土的徐变预测,而且能预测高强钢筋混凝土的徐变,预测结果较实际值有小量偏差,但满足实际工程需求,能够很好地反映配筋对徐变的影响。
4 钢筋修正系数影响因素分析
4.1 混凝土老化系数的影响
文献[16]给出的混凝土老化系数的建议公式 如下:
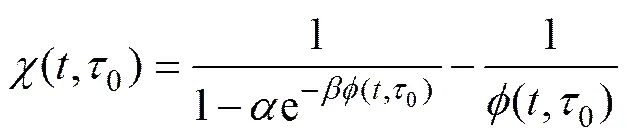
式中:和为常数,对于继效流动理论,=0.91,=0.686;对于老化理论,==1;为混凝土徐变系数。孙宝俊[16]建议取混凝土老化系数=0.8。混凝土老化系数对预测结果的影响如图2所示。
从图2可见:采用不同计算式的混凝土老化系数对钢筋修正系数的预测结果影响很小,预测趋势与实际结果较符合;3种预测结果中,老化理论预测值最大,与实际值最接近,继效流动理论和文献[16]的建议值预测结果基本一致。对于精度要求较高的预测,可以选择式(13)计算的龄期调整混凝土老化系数;对于预测精度要求不高的徐变预测,直接取混凝土老化系数=0.8即可满足要求。
1—文献[12]中钢筋混凝土徐变;2—钢筋修正系数徐变(建议值);3—继效流动理论徐变;4—老化理论徐变。
4.2 配筋率的影响
由钢筋修正系数公式可知,影响钢筋修正系数的因素有配筋率、混凝土老化系数以及混凝土徐变系数。混凝土老化系数通常取0.8,徐变系数采用桥规2004模型。配筋对钢筋修正系数影响时程变化曲线如图3所示。对于徐变系数,混凝土徐变前期发展迅速,后期趋于平缓。前1~2年基本能完成终值徐变的80%~90%,混凝土的终值徐变为初始弹性应变的2~3倍。为更直观地研究配筋对钢筋修正系数的影响,简化计算可取=2.5,不同配筋率对钢筋修正系数的影响如图4所示。
从图3和图4可以看出:钢筋对混凝土的徐变影响较大,钢筋对混凝土的徐变具有抑制作用;配筋率越大,达到平缓阶段所需时间越多,即随着时间推移,徐变增大,钢筋的抑制作用才能充分发挥;当配筋率很小时,配筋对混凝土徐变的相对抑制作用最强、最明显(这里定义相对抑制作用为钢筋修正系数在不同配筋率处切线斜率,即单位配筋率对混凝土徐变抑制作用程度);随着配筋率增大,配筋的相对抑制作用逐渐减小;当配筋率≥10%时,配筋的相对抑制作用基本达到平缓,因此,当配筋率很小时,增大或减小配筋对混凝土徐变影响很大;当配筋率很大时,增加或减小配筋对混凝土徐变影响将不明显。在实际工程中,钢筋配筋率一般不会超过最大配筋率5%,此时,配筋对混凝土徐变的相对抑制仍很明显。从钢筋修正系数看,随着配筋率增大,钢筋修正系数越来越小,配筋对混凝土徐变的影响也越大;当配筋率很小时,钢筋混凝土的徐变和素混凝土的徐变基本一样;当配筋率在0.3%以内时,钢筋混凝土徐变为素混凝土徐变的95%左右,可以认为两者徐变系数基本相近,这与文献[13]中试验结果一致。
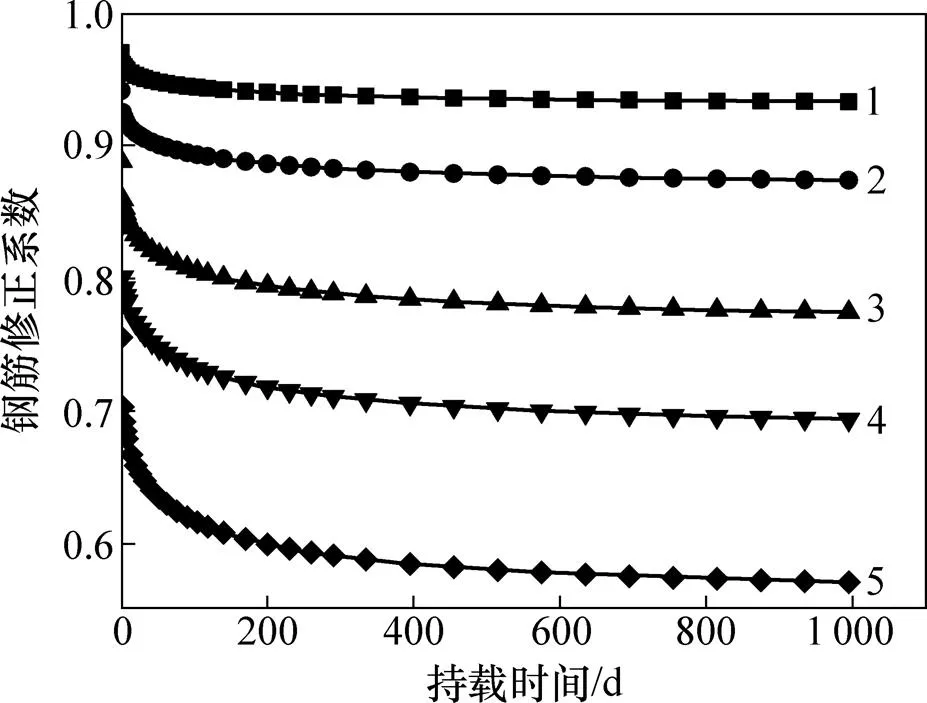
配筋率ρ:1—0.5%; 2—1.0%;3—2.0%;4—3.0%;5—5.0%。
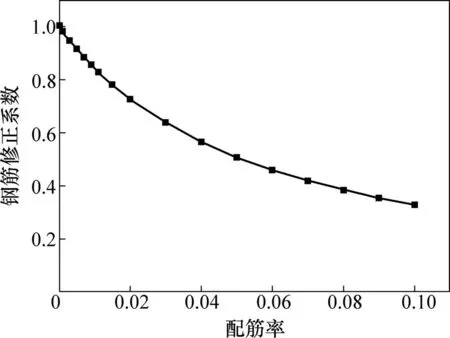
图4 配筋率对钢筋修正系数的影响
4.3 加载龄期的影响
为分析不同加载龄期对钢筋修正系数及配筋混凝土徐变系数的影响,采用钢筋修正系数修正后的徐变预测式(12)计算配筋混凝土徐变。分析结果见图5和图6。
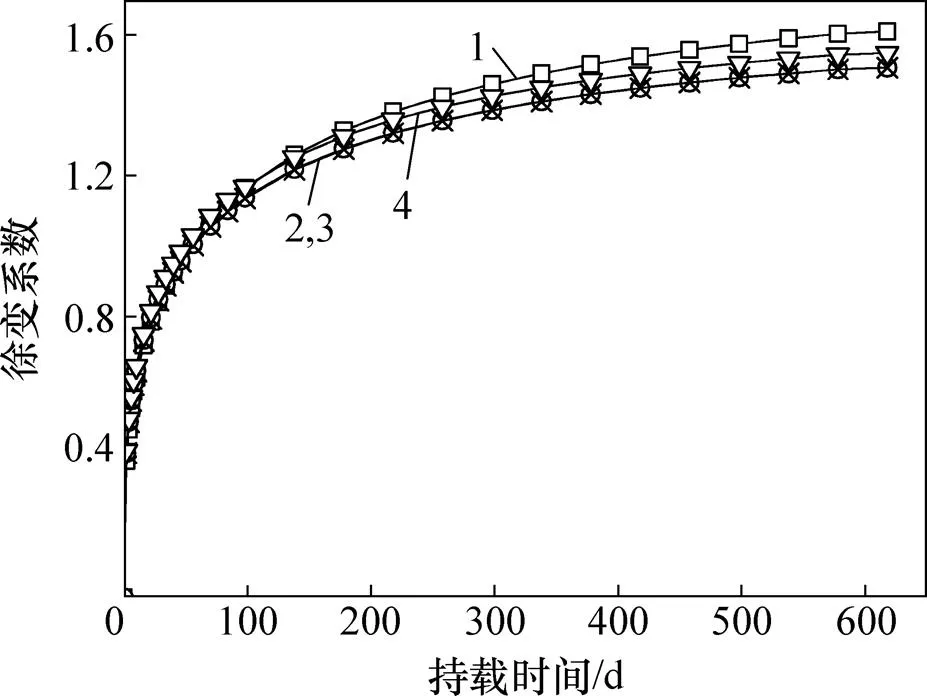
从图5可以看出:在相同配筋率下,加载龄期越大,钢筋修正系数时程变化越小,即加载龄期对配筋的限制作用具有影响;配筋与加载龄期对混凝土徐变都有影响,2种影响具有叠加作用,并且这种叠加作用不只是简单的线性叠加。从图6可见:7 d加载龄期的配筋混凝土徐变系数最大,60 d加载龄期的配筋混凝土徐变系数最小,7 d加载的终值徐变系数分别为14,28和60 d的1.121,1.261和1.438倍,小于素混凝土各龄期徐变系数,这也说明配筋与加载龄期对混凝土的徐变影响具有叠加作用。
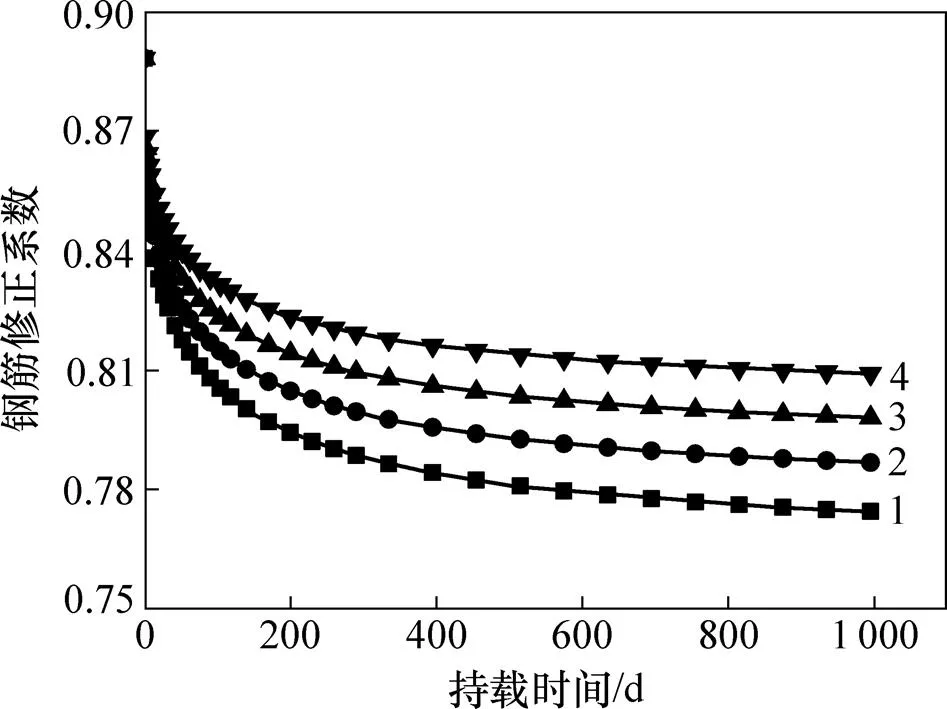
加载龄期/d:1—7;2—14;3—28;4—60。
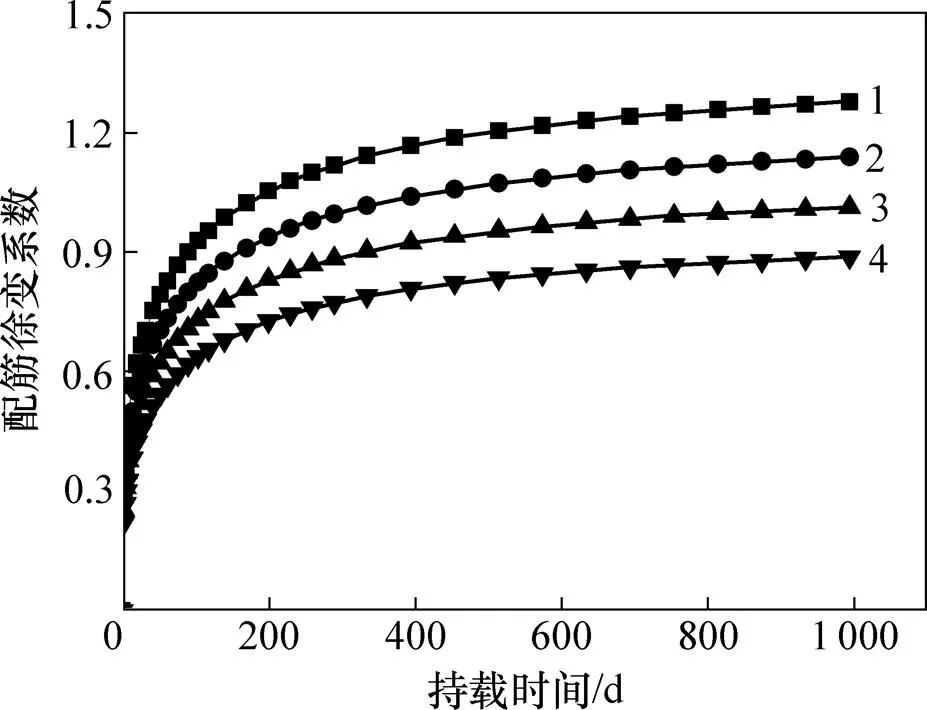
龄期/d:1—7;2—14;3—28;4—60。
5 结论
1) 钢筋修正系数能够很好地预测钢筋混凝土的徐变,且适用高强配筋混凝土。建议采用钢筋修正系数预测配筋混凝土徐变。
2) 配筋对混凝土徐变影响很大。一方面,配筋对混凝土的徐变具有抑制作用,配筋率越大,抑制作用越强;另一方面,当配筋率很小时,配筋对混凝土的相对抑制作用最强;随着配筋率增大,相对抑制作用降低。
3) 加载龄期影响配筋混凝土的徐变,配筋与加载龄期对混凝土徐变都有影响,这2种影响具有叠加作用,并且这种叠加作用不只是简单的线性叠加。
[1] 胡狄, 陈政清. 预应力混凝土桥梁收缩与徐变变形试验研究[J]. 土木工程学报, 2003, 36(8): 79−85. HU Di, CHEN Zhengqing. Experimental research on the deformations for shrinkage and creep of beams in prestressed concrete bridges[J]. China Civil Engineering Journal, 2003, 36(8): 79−85.
[2] BAZANT Z P. Prediction of concrete creep and shrinkage: past, present and future[J]. Nuclear Engineering and Design, 2001, 203(1): 27−38.
[3] 杨小兵. 混凝土收缩徐变预测模型研究[D]. 武汉: 武汉大学土木建筑工程学院, 2004: 15−47. YANG Xiaobing. Research on prediction model of concrete shrinkage and creep[D]. Wuhan: Wuhan University. School of Civil Engineering, 2004: 15−47.
[4] 罗俊礼, 徐志胜, 谢宝超. 不同骨料等级再生混凝土的收缩徐变性能[J]. 中南大学学报(自然科学版), 2013, 44(9): 3815−3822. LUO Junli, XU Zhisheng, XIE Baochao. Shrinkage and creep properties of different grade recycled aggregate concretes[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3815−3822.
[5] 黄国兴, 惠荣炎, 王秀军. 混凝土的徐变与收缩[M]. 北京: 中国电力出版社, 2011: 21−37. HUANG Guoxing, HUI Rongyan, WANG Xiujun. The creep and shrinkage of concrete[M]. Beijing: China Electric Power Press, 2011: 21−37.
[6] 杨健辉, 汪洪菊, 王建生, 等. 高强混凝土收缩徐变试验及模型比较分析[J]. 工业建筑, 2015, 45(3): 120−125. YANG Jianhui, WANG Hongju, WANG Jiansheng, et al. Shrinkage and creep test and comparative analysis of models on high strength concrete[J]. Industrial Construction, 2015, 45(3): 120−125.
[7] 杨永清, 鲁薇薇, 李晓斌, 等. 自然环境混凝土徐变试验和预测模型研究[J]. 西南交通大学学报, 2015, 50(6): 977−983. YANG Yongqing, LU Weiwei, LI Xiaobin, et al. Experimental study and prediction model for concrete creep in ambient environment[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 977−983.
[8] BAZANT Z P. Prediction of concrete creep effects using age adjusted effective modulus method[J]. ACI Journal, 1972, 69(4): 212−217.
[9] JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].
[10] 侯景鹏, 史巍, 袁勇. 钢筋混凝土早龄期约束收缩试验研究[J]. 硅酸盐通报, 2016, 35(1): 292−296. HOU Jingpeng, SHI Wei, YUAN Yong. Restrained shrinkage experiments of reinforced concrete at early age[J]. Bulletin of the Chinese Ceramic Society, 2016, 35(1): 292−296.
[11] 曹国辉, 胡佳星, 张锴. 配筋对混凝土圆柱体长期徐变的影响[J]. 建筑结构, 2015, 45(8): 54−58. CAO Guohui, HU Jiaxing, ZHANG Kai. Influence of reinforcement on long-term creep of concrete circular column[J]. Building Structure, 2015, 45(8): 54−58.
[12] 张克波, 许康, 吕毅刚, 等. 配筋混凝土柱徐变试验[J]. 长沙理工大学学报(自然科学版), 2011, 8(2): 17−20. ZHANG Kebo, XU Kang, LÜ Yigang, et al. Experimental research on creep of reinforced concrete pillars[J]. Journal of Changsha University of Science & Technology (Natural Science), 2011, 8(2): 17−20.
[13] 张运涛, 孟少平, 惠卓. 配筋高性能混凝土收缩徐变试验研究[J]. 建筑科学, 2010, 26(3): 1−5. ZHANG Yuntao, MENG Shaoping, HUI Zhuo. Experimental study on creep and shrinkage of high-performance reinforced concrete[J]. Building Science, 2010, 26(3): 1−5.
[14] 潘钻峰, 吕志涛, 孟少平. 配筋对高强混凝土收缩徐变影响的试验研究[J]. 土木工程学报, 2009, 42(2): 11−16. PAN Zuanfeng, LÜ Zhitao, MENG Shaoping. Experimental study on the influence of steel on high-strength concrete creep and shrinkage[J]. China Civil Engineering Journal, 2009, 42(2): 11−16.
[15] PAN Zuanfeng, LÜ Zhitao, FU C C. Experimental study on creep and shrinkage of high strength plain concrete and reinforced concrete[J]. Advances in Structural Engineering, 2011, 14(2): 235−247.
[16] 孙宝俊. 混凝土徐变理论的有效模量法[J]. 土木工程学报, 1993, 26(3): 66−68. SUN Baojun. The theory of concrete creep effective modulus method[J]. China Civil Engineering Journal, 1993, 26(3): 66−68.
(编辑 陈灿华)
Analysis of reinforcement influence on concrete creep
CAO Guohui1, YANG Liang2, ZHANG Kai1, PENG Xirong1
(1. College of Civil Engineering, Hunan City University, Yiyang 413000, China;2. College of Civil Engineering, Hunan University, Changsha 410082, China)
Based on the age-adjusted effective modulus method (AEMM) and internal force redistribution mechanism, the reinforced correction coefficient was introduced to predict the creep of reinforced concrete and deduce the corresponding calculation formula. The validity and practicability of the reinforced correction coefficient were verified by fitting analysis of the related data. The calculation formula of reinforced concrete creep based on the current code for design of highway reinforced concrete and prestressed concrete bridges and culverts were proposed. Furthermore, the effects of different parameters such as aging coefficient, reinforcement ratio and loading age were analyzed. The results show that reinforcement exerts the inhibitory effect on concrete creep. The inhibitory effect is the strongest when the reinforcement ratio is small and it gradually weakens when the reinforcement ratio increases. Loading age and reinforcement exert additive influences on concrete creep, which is not a simple linear superposition.
reinforced concrete column; creep; reinforced correction coefficient; AEMM method; reinforcement ratio
10.11817/j.issn.1672−7207.2017.02.031
TU311.1
A
1672−7207(2017)02−0506−06
2016−03−10;
2016−05−22
国家自然科学基金资助项目(51551801);湖南省自然科学基金资助项目(14JJ4062);湖南省高等学校科学研究一般项目(13C116)(Project(51551801) supported by the National Natural Science Foundation of China; Project(14JJ4062) supported by the Natural Science Foundation of Hunan Province; Project(13C116) supported by the Scientific Research Project of High School of Hunan Province)
张锴,讲师,从事桥梁受力性能研究;E-mail:349639499@qq.com

