多输入动态调节系统的正交匹配追踪迭代辨识算法
刘艳君,陶太洋,丁锋
多输入动态调节系统的正交匹配追踪迭代辨识算法
刘艳君1, 2,陶太洋1, 3,丁锋1, 2
(1. 江南大学物联网工程学院,江苏无锡,214122;2. 江南大学轻工过程先进控制教育部重点实验室, 江苏无锡,214122;3. 河南中光学集团有限公司,河南南阳,473000)
针对含有未知时滞的多输入单输出动态调节系统,基于过参数化后系统参数向量的稀疏特性,在有限测量数据下,将压缩感知理论和递阶迭代思想相结合,提出一种正交匹配追踪迭代辨识算法。该算法可以辨识多输入动态调节系统的未知时滞、参数和部分阶次。研究结果表明:与最小二乘迭代算法相比,该算法不需要大量的采样数据,可以节约采样成本,提高辨识效率。该算法能够有效地估计这类系统的参数与时滞。
系统辨识;时滞与参数估计;压缩感知;正交匹配追踪;有限采样
系统的参数估计在很多领域如系统辨识[1−3]、自适应控制[4−5]、信号处理[6−7]等得到广泛应用。常规的参数估计算法如最小二乘类算法[8−9]、牛顿迭代算 法[10−11]、随机梯度算法[12]等需要有充分的采样数据才能保证其辨识性能。时滞现象在过程工业中普遍存在且对系统的控制精度有较大的影响,因此,系统的时滞估计也非常重要[13−15]。对于具有未知时滞的多输入动态调节系统,系统参数化后将得到1个高维的参数向量,若采用常规辨识方法则需要大量的采样数据,这将耗费大量的辨识成本, 而且当系统时滞较大时可能带来较大的估计误差。为此,本文作者将寻求一种在有限采样数据下,能够有效辨识这类系统时滞与参数的方法。通常用于控制的系统模型阶次较低,参数化后的系统模型中仅有少量参数。对于含有未知时滞的系统,若不直接考虑时滞,则参数化后的系统模型可由一高维参数向量表示,但该参数向量中仅有少量的非零参数且位置未知,这样的向量称为稀疏向量,由稀疏向量表示的系统称为稀疏系统[16]。压缩感知理论表明: 在一定条件下,稀疏系统可在采样数据量低于系统参数维数的情况下实现系统参数的估计[17−21]。DUMITRESCU等[22]提出一种正交最小二乘算法辨识线性稀疏系统;SANANDAJI等[16]针对含有未知时滞的多输入单输出ARX系统采用分块正交匹配追踪算法,在有限采样数据下估计系统的参数和时滞;LIU等[23]针对白噪声干扰且含有未知时滞的MISO-FIR模型采用阈值正交匹配追踪算法,在有限的采样数据下估计系统的参数和时滞。此外,1范数正则化算法[24]、梯度追踪算法[25]等也相继被提出,用于在有限采样数据下辨识系统的参数和时滞。本文作者将递阶辨识原理和压缩感知重构理论相结合,研究具有未知时滞的多输入动态调节系统。
1 系统描述与问题提出
多输入单输出动态调节系统有如下表述形式[26]:
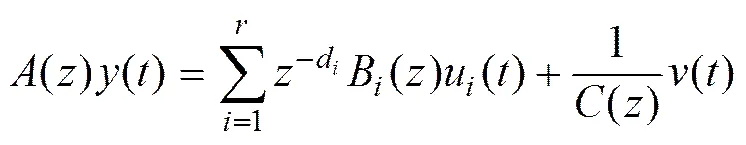
式中:()为系统输出;u()和d分别为第个通道的输入和时滞;()为零均值白噪声;(),B()和()为单位后移算子−1的常系数多项式(−1()=(−1)),可表示为
其中:阶次n和n已知,时滞d和输入通道的阶次n未知。假设当≤0时,()=0,u()=0,()=0。
定义系统的噪声模型
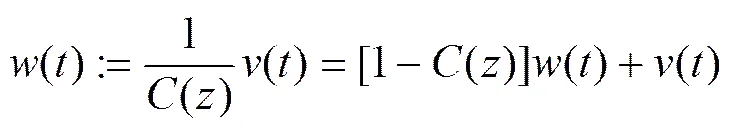
其中:()为噪声模型的输出,是不可测的内部变量。
定义
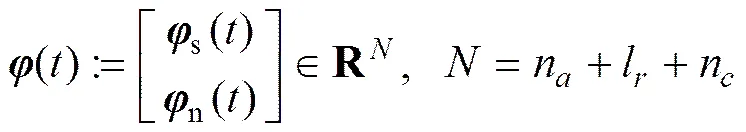
(4)
;
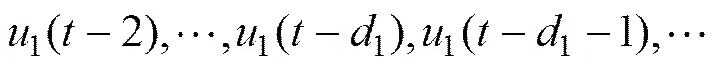
;
;
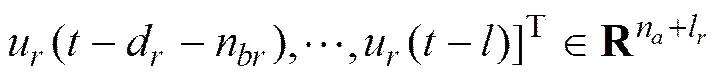
;
;

;
其中:为输入数据回归长度,满足>>;为含有个零元素的零块。
系统模型(1)可写为
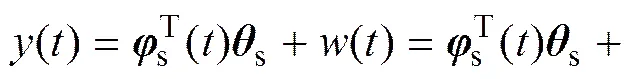
(5)
当=1,2,…,时,可获得组测量数据。定义

则辨识模型(5)可写为如下形式:
(6)
若输入信号持续激励,则参数向量的估计值可由如下最小二乘迭代(LSI)算法得到[13, 27−28]:

;
;
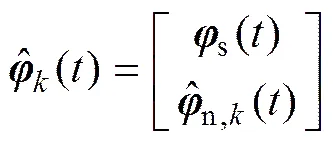


其中:为与时间无关的迭代变量。上述算法要获得良好的参数估计,采样数据量需满足>>。由于参数向量的维数很大,因此,LSI算法辨识系统(1)需要大量的采样数据,将耗费较高的采样成本。
由于参数向量具有稀疏特性,受压缩感知重构理论启发,对上述LSI算法加以改进,使得在有限采样数据量下,可以有效地估计系统参数和时滞。
2 正交匹配追踪迭代算法
辨识模型(6)中,参数向量为稀疏向量。由式(4)可知,参数向量的稀疏度为[29]

很明显稀疏度<<。若输入u()持续激励,则根据压缩感知理论,式(6)在有限采样数据下的辨识问题即为如下最小零范数约束求解问题[21, 29]:
(7)
式中:为设定的允许误差。
根据压缩感知重构理论,在有限的采样数据下,即当<时,式(7)可以通过正交匹配追踪(OMP)算法求解。由于中间变量−(−)未知,导致信息矩阵中含有许多未知项,使得OMP算法不能直接应用。为解决这一问题,借鉴上述LSI算法中的递阶迭代辨识思想:在第次迭代时,未知项−(−)用前一次迭代的估计值代替。换句话说,就是把OMP算法嵌套于迭代算法中。
在第次迭代时,定义

(9)

由式(10)可知:输出向量可以表示为信息矩阵各列的线性组合加上白噪声项的形式。由于参数向量的稀疏性,式(10)等号的右边只有少量的非零项。OMP算法的主要思想就是将这些非零项逐个挑选出来,并对这些非零项参数进行估计。由于OMP算法每次只选出一个非零项,与LSI算法相比,OMP算法只需要较少的测量数据量。

在第次迭代时,将式(6)中的用代替,表示信息矩阵的第列。OMP算法是一种离线的迭代算法,令(为OMP算法的迭代变量)。在第次迭代中的第次OMP迭代,定义准则函数
(12)
由式(12)对求导并令其为0,可得
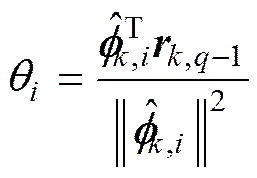
将回代入式(12)可得
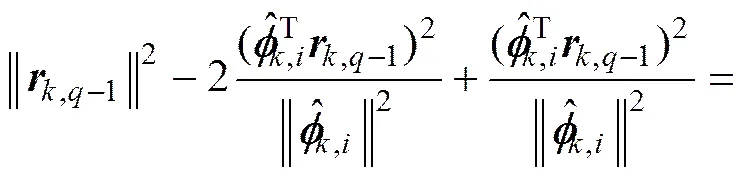
(13)

(15)

(17)
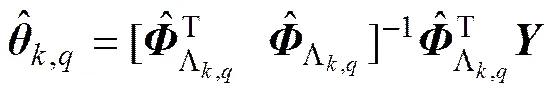
为抑制噪声对参数估计误差的影响,本文通过设定1个很小的阈值H=对每次估计的进行滤波。令为中的第个参数,若,则令,滤波后的估计值记为,并由和更新残差[23, 29]:
(19)
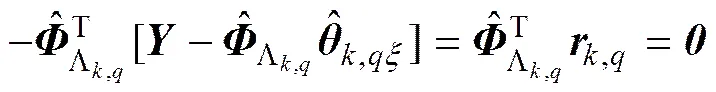
(21)
正交匹配追踪迭代(OMPI)算法的具体实施步骤如下。
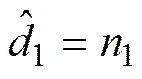
(22)
3 仿真例子
考虑含有时滞的五输入单输出动态调节系统:
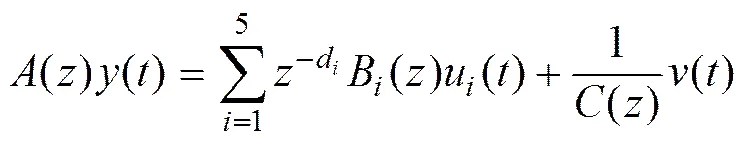
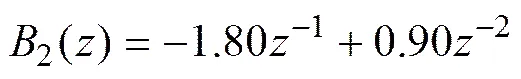

输入通道的时滞分别为1=9,2=23,4=29,5=17,取数据回归长度=40。系统的参数向量为。系统参数向量的维数,稀疏度为。
仿真时,u()采用零均值单位方差不相关可测随机信号,()采用方差为2的零均值白噪声。取数据长度=150。当噪声方差为2=0.102时,分别采用LSI算法和OMPI算法估计系统参数,并使用相同的阀值对LSI的参数估计值予以滤波,参数估计相对误差随迭代次数的变化曲线如图1所示。另外,当噪声方差分别为2=0.102和2=0.502时,采用OMPI算法估计该系统参数,估计误差随迭代次数的变化如图2所示。

1—LSI;2—OMPI。

σ2:1—0.102;2—0.502。
当2=0.102时,OMPI算法得到的参数估计为
(23)
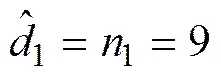
(24)

综合图1、图2和式(23)、(24)有以下结论:
1) 该稀疏系统在有限采样数据量下,OMPI算法的参数辨识精度明显比LSI算法的高。
2) 当噪声方差2=0.502时,OMPI算法的估计精度略低于2=0.102时的估计精度,且所需要的迭代次数也略多于2=0.102时的次数,说明OMPI算法适用于噪声水平不太高的场合。
3) OMPI算法不仅能够有效估计系统的参数,而且能有效地估计系统的未知时滞d以及部分阶次。
4 结论
1) 研究具有未知时滞的多输入单输出动态调节模型的时滞估计和参数辨识问题。结合递阶迭代辨识思想和正交匹配追踪算法,提出一种正交匹配追踪迭代算法。
2) 该算法可以同时估计系统的参数, 未知时滞以及系统中的部分阶次。此外,该算法不需要大量的采样数据,因而可以节约辨识实验中采样成本,提高了辨识效率。仿真结果证明该算法是有效的。
[1] SÖDERSTRÖM T. A generalized instrumental variable estimation method for errors-in-variables identification problems[J]. Automatica, 2011, 47(8): 1656−1666.
[2] DING Feng, DUAN Honghong. Two-stage parameter estimation algorithms for Box-Jenkins systems [J]. IET Signal Processing, 2013, 7(8): 646−654.
[3] DING Feng, LIU Ximei, CHEN Huibo, et al. Hierarchical gradient based and hierarchical least squares based iterative parameter identification for CARARMA systems [J]. Signal Processing, 2014, 97: 31−39.
[4] SHEN Yi, LIU Lijun, DOWELL E H. Adaptive fault-tolerant robust control for a linear system with adaptive fault identification[J]. IET Control Theory and Applications, 2013, 7(2): 246−252.
[5] KELOUWANI S, ADEGNON K, AGBOSSOU K, et al. Online system identification and adaptive control for PEM fuel cell maximum efficiency tracking[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 580−592.
[6] PHILLIP F. Pulse signal and source identification using fuzzy-neural techniques [J]. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(1): 22−33.
[7] SHI Yang, FANG Huazhen. Kalman filter based identification for systems with randomly missing measurements in a network environment [J]. International Journal of Control, 2010, 83(3): 538−551.
[8] LIU Yanjun, DING Feng. Convergence properties of the least squares estimation algorithm for multivariable systems [J]. Applied Mathematical Modelling, 2013, 37(1/2): 476−483.
[9] LIU Yanjun, DING Feng, SHI Yang. Least squares estimation for a class of non-uniformly sampled systems based on the hierarchical identification principle [J]. Circuits, Systems and Signal Processing, 2012, 31(6): 1985−2000.
[10] DING Feng, MA Junxia, XIAO Yongsong. Newton iterative identification for a class of output nonlinear systems with moving average noises [J]. Nonlinear Dynamics, 2013, 74(1/2): 21−30.
[11] LI Junhong, DING Feng, HUA Liang. Maximum likelihood Newton recursive and the Newton iterative estimation algorithms for Hammerstein CARAR systems [J]. Nonlinear Dynamics, 2014, 75(1/2): 235−245.
[12] DING F, LIU Xingao, CHU Jian. Gradient-based and least-squares- based iterative algorithms for Hammerstein systems using the hierarchical identification principle [J]. IET Control Theory and Applications, 2013, 7(2): 176−184.
[13] 丁锋. 系统辨识新论[M]. 北京: 科学出版社, 2013: 199−220. DING Feng. System identification-new theory and methods [M]. Beijing: Science Press, 2013: 199−220.
[14] 王贞, 吴斌. 基于最小二乘法的时滞实时在线估计方法[J]. 振动工程学报, 2009, 22(6): 625−631. WANG Zhen, WU Bin. A real-time approach to delay estimation based on the Least-Square algorithm [J]. Journal of Vibration Engineering, 2009, 22(6): 625−631.
[15] 王建宏, 王道波, 王志胜. 多个未知时延的MISO系统的递推辨识[J]. 控制与决策, 2010, 25(1): 93−98. WANG Jianhong, WANG Daobo, WANG Zhisheng. Recursive identification of MISO systems with multiple unknown time delays [J]. Control and Decision, 2010, 25(1): 93−98.
[16] SANANDAJI B M, VINCENT T L, WAKIN M B, et al. Compressive system identification of LTI and LTV ARX models [C]//Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando, Florida, USA, 2011: 791−798.
[17] DONOHO D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289−1306.
[18] CANDÈS E J. Robust uncertainty principles: Extra signal reconstruction from highly frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489−509.
[19] CANDÈS E J, ROMBERG J R, TAO T. Stable signal recovery from incomplete and inaccurate measurements [J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207−1223.
[20] CANDÈS E J, WAKIN M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21−30.
[21] TROPP J A. Greed is good: algorithmic results for sparse approximation [J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231−2242.
[22] DUMITRESCU B, ONOSE A, HELIN P, et al. Greedy sparse RLS [J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2194−2207.
[23] LIU Yanjun, TAO Taiyang. A CS recovery algorithm for model and time-delay identification of MISO-FIR systems [J]. Algorithms, 2015, 8(3): 743−753.
[24] TÓTH R, SANANDAJI B M, POOLLA K, et al. Compressive system identification in the linear time-invariant framework [C]//Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando, Florida, USA, 2011: 783−790.
[25] BLUMENSATH T, DAVIES M E. Gradient Pursuits [J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2370−2382.
[26] 丁锋. 系统辨识(2): 系统描述的基本模型[J]. 南京信息工程大学学报(自然科学版), 2011, 3(2): 97−117. DING Feng. System identification (Part B): basic models for system description [J]. Journal of Nanjing University of Information Science & Technology (Natural Science Edition), 2011, 3(2): 97−117.
[27] LI Xiangli, DING Ruifeng, ZHOU Lincheng. Least squares based iterative identification algorithm for Hammerstein nonlinear systems with non-uniform sampling [J]. International Journal of Computer Mathematics, 2013, 90(7): 1524−1534.
[28] WANG Dongqin, DING Feng. Least squares based and gradient based iterative identification for Wiener nonlinear systems [J]. Signal Processing, 2011, 91(5): 1182−1189.
[29] ELAD M. Sparse and redundant representions: From theory to applications in signal and image processing [M]. New York: Springer-Verlag, 2010: 20−62.
(编辑 陈爱华)
Parameter and time-delay estimation for MISO dynamic adjustment systems based on orthogonal matching pursuit iterative algorithm
LIU Yanjun1, 2, TAO Taiyang1, 3, DING Feng1, 2
(1. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China;2. Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education),Jiangnan University, Wuxi 214122, China;3. Henan Costar Group Company Limited, Nanyang 473000, China)
For multiple-input dynamic adjustment systems with unknown time delays, based on the characteristics of sparsity of the over parameterized parameter vector, and by combining the orthogonal matching pursuit algorithm with the hierarchical iterative idea, an orthogonal matching pursuit iterative (OMPI) identification algorithm was presented. This algorithm can estimate the parameters, time delays and some of the orders of the multiple-input dynamic adjustment systems with limited sampled data. The results show that the proposed method can effectively reduce the measuring cost, and improve the identification efficiency since it requires only a small number of sampled data compared to conventional identification methods such as the least square iterative (LSI) method. The proposed algorithm can effectively estimate the parameters and time delays of such sparse systems.
system identification; parameter and time delays estimation; compressed sensing; orthogonal matching pursuit algorithm; limited sampled data
10.11817/j.issn.1672−7207.2017.02.017
TP273
A
1672−7207(2017)02−0389−06
2016−04−05;
2016−07−25
国家自然科学基金资助项目(61304138);江苏省自然科学基金资助项目(BK20130163)(Project(61304138) supported by the National Natural Science Foundation of China; Project(BK20130163) supported by the Natural Science Foundation of Jiangsu Province, China)
刘艳君,博士,副教授,从事系统辨识、自适应控制等研究;E-mail:yanjunliu_1983@126.com

