初始损伤对脆性岩石抗压力学性质的影响
陈乐求,张家生,陈俊桦, 陈积光
初始损伤对脆性岩石抗压力学性质的影响
陈乐求1, 2,张家生1,陈俊桦1, 陈积光2
(1. 中南大学土木工程学院,湖南长沙,410075;2. 湖南理工学院土木建筑工程学院,湖南岳阳,414006)
基于现有各向同性损伤本构理论,提出岩石初始损伤定义及其计算方法。初始损伤表示为加载前的损伤岩石弹性模量相对无损岩石弹性模量的劣化程度。对不同初始损伤的玄武岩试样进行单轴抗压试验,定量分析初始损伤对玄武岩的应力与应变关系、强度、破坏应变、初始泊松比和应变软化性质等的影响,给出单轴抗压强度、初始泊松比等力学参数随初始损伤变量变化的规律及拟合公式。研究结果表明:只有当岩石初始损伤超过损伤门槛值即无损岩石破坏时对应的损伤值时,岩石抗压强度随初始损伤增大而显著减小;与峰值应力对应的应变随初始损伤增大而近似呈线性增大趋势;岩石初始泊松比随初始损伤增大近似呈指数增大;初始损伤越小,应力峰值后的岩石破坏越显脆性。
岩石;损伤;单轴抗压强度;弹性模量;脆性破坏
受地质构造运动、温度等外部因素的影响,天然岩石一般为内部含孔隙和裂纹等缺陷的材料。这些缺陷所在部位往往容易产生应力集中,从而影响岩石的宏观力学性质。目前,损伤力学理论是研究岩石力学行为的成熟理论,根据该理论,若将岩石内部既有缺陷看作初始损伤,则工程岩体内部的各种结构面是初始损伤的宏观表现。由于工程中岩石一般处于受压状态,因此,研究初始损伤对岩石抗压力学性质的影响规律具有重要工程应用价值。数值分析已经成为理论研究在工程中应用的重要方法,合理的本构模型是数值计算结果具备实用性的前提条件。虽然李冰洋 等[1−10]通过室内常规三轴试验研究了初始损伤对岩石抗压力学性质的影响,但这些研究成果不方便在工程中应用,其原因主要是这些研究成果中的初始损伤定义未能很好地与目前常用损伤本构模型(一般为各向同性损伤本构模型)联系在一起。虽然这种初始损伤定义比较接近实际情况,但考虑的因素过多,既有裂纹数量也有裂纹方向,损伤演化过程过于复杂,因此,这些研究一般只能用于反映初始损伤影响抗压强度的规律,很难用于深入分析初始损伤对岩石扩容和应变软化等性质的影响。此外,适应于这种初始损伤定义的本构模型一般为各向异性损伤本构模型,目前,各向异性损伤本构模型过于复杂,很难在工程实际中推广。邱士利等[5]以岩石抗压强度的百分比作为初始损伤值,实际上是将岩石损伤看作是各向同性,忽略岩石内部缺陷的方向性对损伤的影响,从而较容易获取初始损伤的影响规律。但由于常用损伤本构模型一般以损伤变量(或者损伤因子)表示弹性模量、密度等参数的劣化,故邱士利等[5]提出的这种初始损伤定义也很难与常用损伤本构模型相联系。陈俊桦等[11−13]基于常用岩石爆破损伤本构模型提出了与模型中损伤变量对应的初始损伤变量。这些研究中的初始损伤定义简单,不仅方便与本构模型联系,而且与工程上的岩体完整性指数相关,便于工程应用,为岩石初始损伤的定义提供了一种思路。在工程应用范围内,一般可将岩石近似看作各向同性材料,且实际工程中岩石受压状态较复杂,单向受压状态下的岩石力学性质比三向受压状态简单。为此,本文作者从现有各向同性损伤模型出发,提出相应于各向同性损伤本构模型的初始损伤定义。然后通过单轴抗压试验研究初始损伤对脆性岩石力学性质的影响,以便为考虑初始损伤影响的岩石本构理论研究和工程应用提供参考。
1 初始损伤定义
初始损伤定义与常用本构模型相关。目前常用的岩石本构模型为各向同性损伤本构模型。各向同性损伤本构模型,常用利用损伤变量表示弹性模量、声波波速和密度等宏观力学参数的劣化程度[14−15]。大变形损伤时,一般采用密度的变化衡量固体材料的损伤−劣化。对于小变形范围内的固体材料损伤,一般采用弹性模量的变化衡量。一般来说,岩石属于小变形范围内发生破坏的脆性材料,因此,岩石,特别是硬岩等脆性岩石,一般可以看作各向同性弹性损伤材料。各向同性损伤变量计算公式为
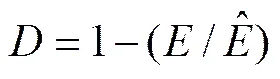
式中:为损伤变量,0≤≤1;为损伤岩石的弹性模量;为无损岩石的弹性模量。
从式(1)可看出现有损伤本构模型将岩石看作无损材料。在加载过程中,损伤发生变化将导致岩石由无损状态向损伤状态转变,同时弹性模量不断降低。而工程中的岩石一般为初始损伤材料,即人工扰动未发生前,岩石已经处于一定损伤状态。根据式(1),对于初始损伤岩石,有下式成立:

式中:0为未加载前损伤岩石的初始损伤变量;0为损伤岩石的初始弹性模量。从式(2)可看出:无损岩石的弹性模量即为初始损伤弹性模量,无损岩石的初始损伤变量0=0;对于初始损伤岩石,只有当0和确定后,才能计算得到岩石初始损伤值0;0一般可由室内试验的岩石应力与应变关系曲线获取。而由于天然岩石一般不是无损材料,较难直接获取无损岩石弹性模量。为此,参考文献[11−13]中方法,在完整岩体内取岩样,然后在单轴抗压试验和利用统计方法处理试验结果的基础上,近似获得无损岩样的弹性模量。对于不同初始损伤岩石的抗压强度试验,无损弹性模量还应满足下式:
(3)
根据式(1)和(2)可以计算岩石初始损伤,并将初始损伤与常用的各向同性损伤本构模型相联系。
2 初始损伤岩石的单轴抗压试验
岩石试样为灰色、致密状极硬玄武岩。岩石天然密度密度为2.7~3.0 g/cm3,岩石试样为标准圆柱试样,其直径为5 cm,高为10 cm。选取裂隙发育程度不同的岩石试样,以位移控制模式施加轴向荷载,在0.08 mm/min的加载速率下进行岩石单轴抗压试验。
3 试验结果及分析
无损弹性模量近似取值为58.0 GPa。选取8个用于分析的岩石试样,它们的初始弹性模量0分别58.0,55.1,52.2,49.3,46.4,37.7,29.0和23.3 GPa。根据式(2)计算得到各个岩石试样的初始损伤值0分别为0,0.05,0.10,0.15,0.20,0.35,0.50和0.60。
3.1 初始损伤对岩石应力与应变关系的影响
图1所示为不同初始损伤岩石的轴向应力a与轴向应变a的部分关系曲线。
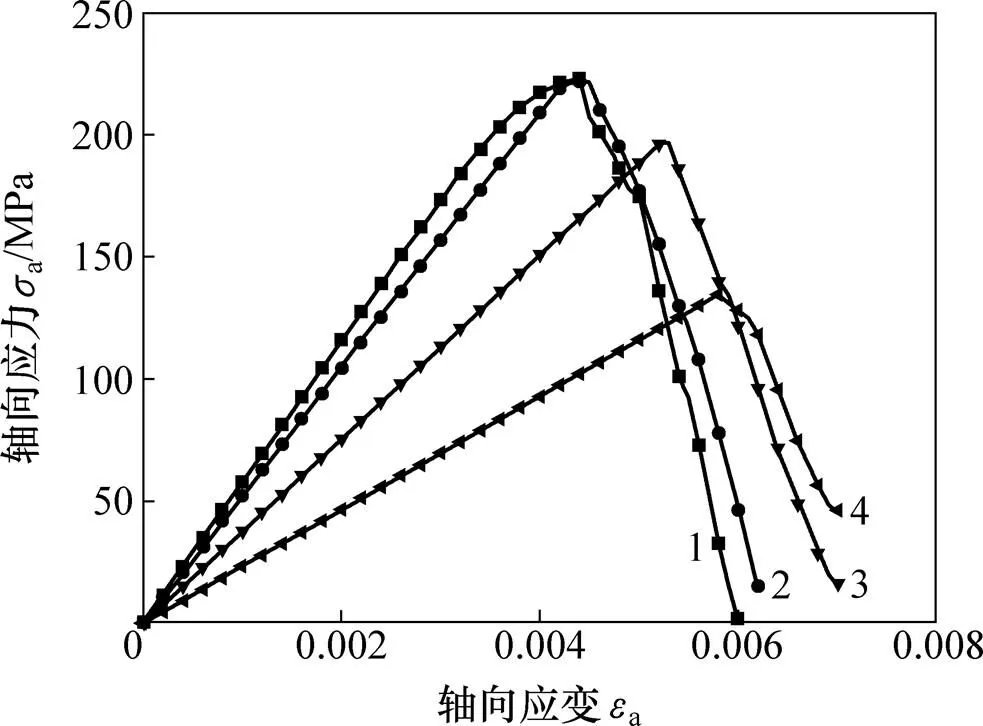
初始损伤D0:1—0;2—0.10;3—0.35;4—0.60。
从图1可见:在应力峰值前,不同初始损伤岩石的应力与应变关系基本呈线性发展;曲线的斜率和初始损伤弹性模量差别不大;应力达到峰值前,岩石的应力与应变关系近似为弹性关系;峰值应力后,各条曲线中应力与应变关系表现为应变软化,应力随变形增加而快速下降,即峰值后曲线形态较相似。由以上分析可知:试验中的玄武岩为弹脆性硬岩,其应力与应变关系一般可近似利用弹性损伤理论进行分析。
根据岩石加载记忆现象,循环逐级加卸载条件下的岩石应力和应变关系曲线的外包线与单调连续加载下的全应力和应变关系曲线基本重合[16]。弹脆性无损岩石的记忆效应简化理论模型如图2所示。图2中:为单轴连续加载曲线;为单轴加卸载条件下的其中1条卸载−再加载曲线;和等为循环逐级加卸载曲线中的卸载与再加载路径,简化为直线段。不考虑黏滞性和加载应变率等因素的影响时(拟静力加卸载),理论上卸载与再加载的直线段是重合的。在各向同性弹性损伤力学假设成立的前提下,各初始损伤岩石实际上均可看作由无损岩石的卸载形成。初始损伤弹性模量由图2中等虚线的斜率确定,即任意初始损伤岩石的初始损伤值均可由无损岩石的损伤演化计算得到。由于初始损伤岩石保留了无损岩石加载过程中各个损伤时刻的加载历史,所以,必然会出现图2所示的各个初始损伤岩石在损伤发展过程中的加载路径和无损岩石重合的现象。而由图1可知,试验结果和理论预测结果之间存在差距。初始损伤岩石的加载路径并没有与无损岩石的加载路径完全重合,它们之间有一定差距,特别是峰值后的曲线,这是由损伤的扩展特点等决定的。损伤扩展特别是峰值应力后的宏观裂隙发展阶段,即使应力峰值前的岩石为各向同性体,峰值后的岩石实际上也不是各向同性体。而各向异性这种力学性质对应力加载路径影响很大。此外,自然界并不存在天然的无损岩石,引起各个岩石试件初始损伤的应力环境也很难完全一样。故试验中损伤岩石在应力峰值后的应力与应变关系曲线无法完全与近似无损岩石的一致。
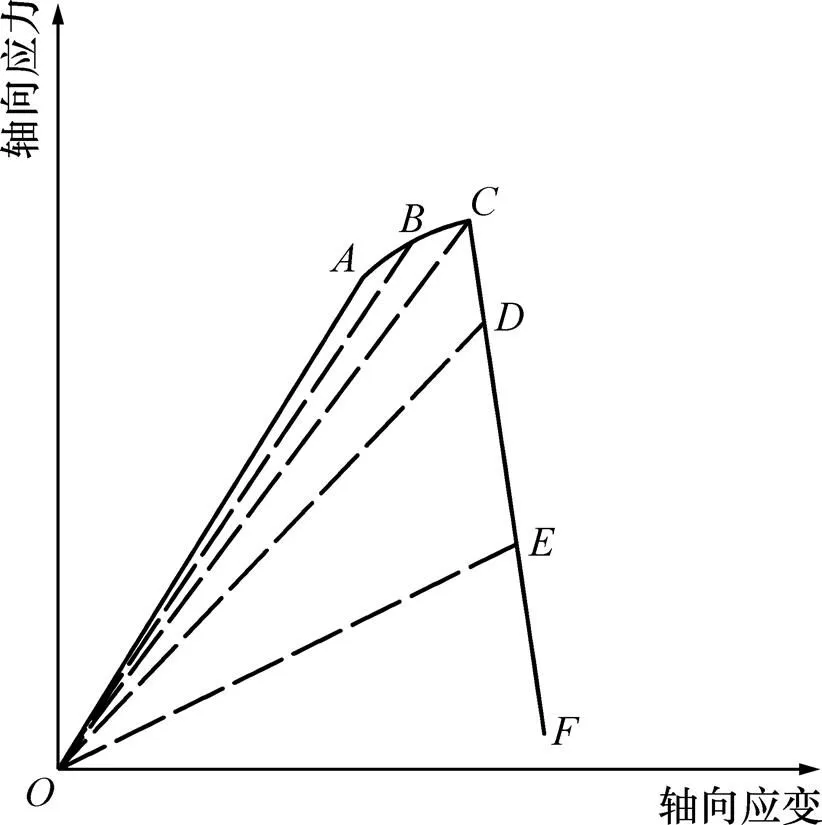
1—单轴连续加载曲线;2—循环逐级加卸载曲线。
3.2 初始损伤对岩石抗压强度以及破坏变形的影响
3.2.1 初始损伤与抗压强度
从图1可看出:随着初始损伤增大,岩石抗压强度逐渐减小。根据损伤力学理论,假设对应峰值应力或者抗压强度的损伤变量由式(1)计算如下:
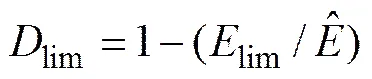
式中:lim为岩石损伤门槛值;lim为与峰值应力点对应的变形模量或损伤弹性模量。
为方便结合损伤力学理论探讨损伤变化规律,以图2中脆性无损硬岩的单轴连续加载全应力与应变关系曲线示意图为例,分析岩石损伤变化过程。图2中,段可以看作为线弹性变形阶段,此时≤0=0,即该阶段为损伤未扩展阶段。随着加载应力水平增大,岩石中微裂纹稳定扩展,损伤变量满足0<≤lim,即损伤发展处于稳定阶段。此阶段的应力与应变关系曲线为段非线性曲线。点可看作弹性比例极限,点为抗压强度或者峰值应力点。由前面对岩石加载记忆性现象的分析可知,无损岩石的损伤门槛值代表了岩石产生宏观形式裂纹的最低损伤门槛值。当应力达到峰值点后,出现应变软化现象,此时,>lim,表示损伤劣化阶段从微裂纹扩展阶段进入宏观形式裂纹的扩展阶段。此阶段属于非稳定损伤发展阶段,其应力与应变关系曲线为段曲线,呈下降趋势。
岩石单轴抗压强度c、初始损伤0以及lim之间的关系见图3。图3中,lim=0.13为初始无损玄武岩试样发生破坏时的损伤值。由于试验中试样初始损伤和加载过程累积的损伤均相对无损状态,即损伤为相对初始无损岩石力学性质的劣化,故初始无损岩石的损伤门槛值lim=0.13是评价岩石损伤变化的重要参数。从图3可看出不同初始损伤岩石的0和lim之间满足以下关系式:

由式(5)可以看出,当损伤岩石的初始损伤0超过初始无损岩石的损伤门槛值0.13时,初始损伤岩石的损伤门槛值与其初始损伤度相同。由前面分析可知,lim=0.13为表征宏观形式裂纹产生的最低损伤门槛值,因此,可推断0>0.13对应的初始损伤岩石的内部存在宏观形式的裂纹。
从图3还可以看出,当岩石初始损伤0≤0.13,即对于由内部微裂纹确定初始损伤的岩石,其抗压强度几乎不变。当0>0.13,即对于由宏观形式裂纹决定初始损伤的岩石,其抗压强度随着初始损伤的增大而逐渐减小,且这种减小趋势随初始损伤增大而越来越显著。因此,损伤劣化起主要作用的阶段为宏观形式裂纹的非稳定扩展阶段。如图1中,应力峰值后,各个初始损伤岩石均处于伴随着宏观裂纹发展的非稳定变形中。
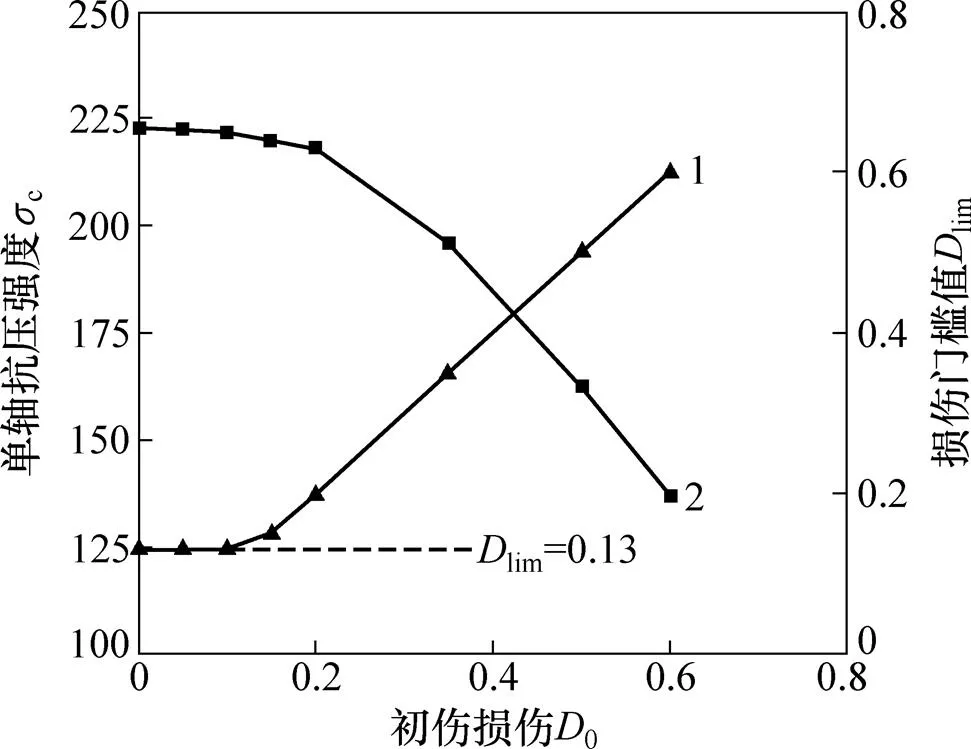
1—损伤门槛值;2—单轴抗压强度。
3.2.2 初始损伤与破坏变形
不同初始损伤岩石的峰值应力对应的应变c与其初始损伤值0之间的关系见图4。从图4可看出:峰值应力对应的应变与初始损伤近似呈线性递增关系,即岩石的破坏变形随初始损伤增大而增大。图4中,由数据拟合得到的公式为
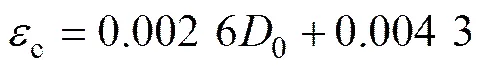
式中:初始损伤满足0≤0≤0.6。相关系数约为0.99,即c与0之间的线性关系显著。
根据弹性损伤假设以及由图2可知:随着初始损伤增大,等虚线的斜率逐渐降低,~各峰值应力点对应的应变依次不断增大。可见试验结果与由岩石加载记忆性理论得到的结果相符。
3.3 初始损伤对岩石初始泊松比的影响
设岩石的初始泊松比为0。初始泊松比0与损伤泊松比的关系见图5。从图5可见:岩石初始泊松比近似随初始损伤增大而增大。采用指数函数对数据进行拟合,得到如下关系式:

式中:0≤0≤0.6,拟合相关系数为0.92。
图5 岩石初始泊松比和初始损伤的关系
Fig. 5 Relationship between initial Poisson ratio and initial damage
在单轴加载条件下,初始泊松比反映了加载弹性阶段中圆柱试样轴向变形对其径向变形的影响程度。由试验结果可知,相同轴向应变引起的径向应变随初始损伤增大而增大。在本文各向同性损伤假设条件下,初始损伤的存在使得径向变形对损伤的敏感度增大,因此,若有围压作用,则径向变形将受到压力约束,初始损伤对泊松比的影响将降低。
与初始弹性模量一样,若不同初始损伤岩石的初始泊松比可看作无损岩石加载过程中对应其不同损伤时刻的损伤泊松比或者表观泊松比,则根据本文提出的初始损伤理论,损伤泊松比或者表观泊松比随损伤的增大而增大,这与由混凝土、岩石等脆性材料的抗压试验研究得到的结论相符[17],这些以裂纹扩展导致破坏的材料在受压过程中往往表现出剪胀或者表观泊松比增大的现象。
3.4 初始损伤对岩石应变软化性质的影响
从图1可看出:初始损伤越大,应力峰值后曲线下降速率越慢。为定量考虑不同初始损伤岩石的峰值后应变软化程度,定义应变软化模量为

式中:为应变软化模量,越大,应力峰值后的曲线越陡,应变软化程度越显著,即应力峰值后的破坏越显脆性,当∞时,岩石发生完全脆性破坏;f和f分别为试验中岩石完全破裂时的应力和应变。岩石完全破裂点一般如图2中的点所示。
由图1可知:不同初始损伤岩石的完全破裂点不同。利用式(8)可计算不同初始损伤岩石峰值点后的应变软化程度。初始损伤0与应变软化模量之间的关系见图6。从图6可看出:总体趋势上,随着初始损伤增大,应变软化模量减小,因此,随着初始损伤增大,岩石应变软化程度降低,或者随着初始损伤减小,应力峰值后岩石脆性破坏越显。葛修润等[18]也认为,峰值后应力与应变关系曲线下降越快,岩石脆性越显著。总体上,对于不同初始损伤的岩石,应变软化模量均比相应的岩石初始损伤弹性模量大很多,即应力与应变关系曲线的下降段比上升段陡,故由应变软化性质分析得到的结论也反映出试验中的玄武岩为脆性破坏岩石。图6中拟合曲线的数学表达式为

式中:0≤0≤0.6,拟合相关系数为0.98。
图6 应变软化模量与初始损伤的关系
Fig. 6 Relationship between strain softening modulus and initial damage
4 初始损伤定义的工程应用分析
式(1)和(2)中损伤变量和初始损伤定义是基于各向同性损伤本构关系提出的。不同损伤程度对应的破坏机理不同。在通常情况下,当损伤变量较小时,岩石力学性质劣化主要由微观裂纹扩展决定;反之,则主要由宏观裂纹扩展决定。岩石材料在工程中的应用对象一般称为岩体[12]。岩体内部常见宏观缺陷为节理裂隙、错动带和断层等,因此,岩体初始损伤一般较大,其力学性能一般比构成岩体的基本单元即岩块的力学性能差。
工程中很少直接测量岩体弹性模量,故一般不直接利用式(1)和(2)计算岩体初始损伤值。无论是初始损伤还是损伤变量,它们实质上均是反映材料力学性质劣化的内变量。一般将该变量与表观可测物理量相联系,故岩体的初始损伤定义应与工程上常用的物理量相联系。洞室围岩位移、围岩声波波速和岩体完整性指数等均是工程上评价岩体开挖质量的常用物理量,可在这些物理量中选取合适的量定义初始损伤。
朱传云等[19]建立了损伤变量和岩体完整性指数的关系式。文献[11−13]则在文献[19]的基础上,提出了工程中计算初始损伤0的表达式:
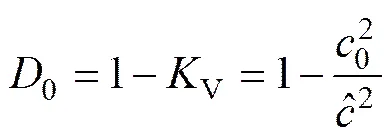
式中:V为岩体完整性指数;0和分别为损伤岩体的初始声波波速和无损岩体声波波速。根据一维应力理论,由钻孔声波法测得的声波波速和弹性模量的关系为
(11)
根据式(10),定义的初始损伤0可以与工程中常用的岩体完整性指数以及声波波速等相联系。在施工部位利用钻孔声波法即可获得该部位岩体的初始损伤值。由于钻孔声波法是工程中常用的安全监测方法,故由式(10)定义和计算得到的初始损伤变量方便工程应用。
需要指出的是:宏观结构面引起的初始损伤及该结构面的损伤演化扩展往往伴随着各向异性、尺寸效应等现象;岩体初始损伤越大,本文提出的各向同性初始损伤定义的适用性越差。此外,当初始损伤较大时,即使对于室内试验也会造成困难,如初始损伤越大时,制样、取样越困难。对于工程应用,本文提出的各向同性损伤变量及初始损伤变量的定义应该有一个适用范围,该适用范围还有待进一步研究。
5 结论
1) 基于各向同性损伤本构理论提出了相对无损岩石材料的初始损伤定义,并给出了计算脆性岩石初始损伤的方法。提出的初始损伤定义方便采用现有损伤理论定量分析初始损伤对脆性岩石抗压力学性质的影响及总结相关的影响规律,有利于加深对岩石抗压损伤机理的认识。
2) 存在与岩石破坏强度有重要联系的损伤变量门槛值,该值为无损岩石抗压变形过程中应力到达峰值时对应的损伤值。当岩石的初始损伤值超过该损伤门槛值时,岩石抗压强度随初始损伤增大而显著减小。
3) 峰值应力对应的应变随着初始损伤的增大而不断增大,且近似呈线性递增。随着初始损伤增大,岩石初始泊松比增大;应力峰值后岩石的应变软化程度降低,岩石破坏表现出的脆性程度降低。
4) 岩石或多或少地会表现出各向异性的力学性质,而本文将岩石看作各向同性损伤材料,这导致研究结果与实际情况有差别。但是,因为现有针对岩石力学性质研究的成熟理论一般将岩石看作各向同性材料,且本文所提出的初始损伤定义能与各向同性损伤本构模型以及工程实际相联系,故研究成果便于应用,对相关理论研究也有一定的参考价值。
[1] 李冰洋, 尤明庆. 正则抛物线准则及岩石初始损伤的估计[J]. 岩土工程学报, 2015, 37(9): 1740−1744. LI Bingyang, YOU Mingqing. Normal parabolic criterion and estimation of initial damage of rock[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1740−1744.
[2] 张利洁, 朱杰兵, 骆建宇, 等. 岩石初始损伤及其对单轴抗压强度的影响研究[J].长江科学院院报, 2014, 31(11): 22−37. ZHANG Lijie, ZHU Jiebing, LUO Jianyu, et al. Initial damage of rock and its defects on uniaxial compressive strength of rock[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(11): 22−37.
[3] 汪亦显. 含水及初始损伤岩体损伤断裂机理与实验研究[D]. 长沙: 中南大学资源与安全工程学院, 2012: 63−80. WANG Yixian. Damage weakening and fracture failure mechanism for rock mass concerning influence of water and initial defects[D]. Changsha: School of Resources and Safely Engineering. Central South University, 2012: 63−80.
[4] 陈有亮, 代明星, 刘明亮, 等. 含初始损伤岩石的冻融损伤试验研究[J]. 质量检测, 2013, 34(1): 74−80. CHEN Youliang, DAI Mingxing, LIU Mingliang, et al. Experimental investigation on freezing damage characteristics of granite with initial damage[J]. Chinese Quarterly of Mechanics, 2013, 34(1): 74−80.
[5] 邱士利, 冯夏庭, 张传庆, 等. 不同初始损伤和卸荷路径下深埋大理岩卸荷力学特性试验研究[J]. 岩石力学与工程学报, 2012, 31(8): 1686−1697. QIU Shili, FENG Xiating, ZHANG Chuanqing, et al. Experimental research on mechanical properties of deep marble under different initial damage levels and unloading paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1686−1697.
[6] 白晨光, 魏一鸣, 朱建明. 岩石材料初始缺陷的分维数与损伤演化的关系[J]. 矿冶, 1996, 5(4): 17−19. BAI Chenguang, WEI Yiming, ZHU Jianming. The relation between dimension of defects of rock material and its damage evolution[J]. Ming & Metallurgy, 1996, 5(4): 17−19.
[7] 王国艳, 李树忱, 杨磊. 初始损伤对岩体力学性质影响的试验研究[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(6): 909−912. WANG Guoyan, LI Shuchen, YANG Lei. Test study of mechanical properties for rock mass including initial damage[J]. Journal of Liaoning Technical University(Natural Science), 2009, 28(6): 909−912.
[8] 凌建明. 压缩荷载条件下岩石细观损伤特征的研究[J]. 同济大学学报, 1993, 21(2): 219−226. LING Jianming. Study on the mesoscopical characteristics of rock damage under compressive loading[J]. Journal of TongJi University, 1993, 21(2): 219−226.
[9] 袁小清, 刘红岩, 刘京平. 非贯通裂隙岩体三维复合损伤本构模型[J]. 岩土工程学报, 2016, 38(1): 91−99. YUAN Xiaoqing, LIU Hongyan, LIU Jingping. 3-D constitutive model for rock masses with non-persistent joints based on compound damage[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 91−99.
[10] 李宏哲, 夏才初, 王晓东, 等. 含节理大理岩变形和强度特性的试验研究[J]. 岩石力学与工程学报, 2008, 27(10): 2118−2123. LI Hongzhe, XIA Caichu, WANG Xiaodong, et al. Experimental study on deformation and strength properties of jointed marble specimens[J]. Chinese Journal of Geotechnical Engineering, 2008, 27(10): 2118−2123.
[11] 陈俊桦, 李新平, 张家生. 基于爆破损伤的岩台保护层开挖爆破参数研究[J]. 岩石力学与工程学报, 2016, 35(1): 98−108. CHEN Junhua, LI Xingpin, ZHANG Jiasheng. Study on blasting parameters of protective layer excavation of rock bench based on blasting-induced damage[J]. Chinese Journal of Geotechnical Engineering, 2016, 35(1): 98−108.
[12] 陈俊桦, 张家生, 李新平. 考虑岩体完整程度的岩石爆破损伤模型及应用[J]. 岩土工程学报, 2016, 38(5): 857−866. CHEN Junhua, ZHANG Jiasheng, LI Xinping. Model of rock blasting-induced damage and its application based on the integrity of rockmass[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 857−866.
[13] 陈俊桦, 张家生, 李新平. 基于岩石爆破损伤理论的预裂爆破参数研究及应用[J]. 岩土力学, 2016, 37(5): 1441−1450. CHEN Junhua, ZHANG Jiasheng, LI Xinping. Study of presplitting blasting parameters and its application based on rock blasting-induced damage theory[J]. Rock and Soil Mechanics, 2016, 37(5): 1441−1450.
[14] 张全胜, 杨更社, 任建喜. 岩石损伤变量及本构方程的新探讨[J]. 岩石力学与工程学报, 2003, 22(1): 30−34. ZHNAG Qunasheng, YANG Gengshe, REN Jianxi. New study of damage variable and constitutive equation of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 30−34.
[15] 刘红岩, 王根旺, 刘国振. 以损伤变量为特征的岩石损伤理论研究进展[J]. 爆破器材, 2004, 33(6): 25−29. LIU Hongyan, WANG Genwang, LIU Guozhen. Research development of rock damage theory characterized by damage variable[J]. Explosive Materials, 2004, 33(6): 25−29.
[16] 杨春和, 马洪岭, 刘建锋. 循环加、卸载下盐岩变形特性试验研究[J]. 岩土力学, 2009, 30(12): 3562−3567. YANG Chunhe, MA Hongling, LIU Jianfeng. Study of deformation of rock salt under cycling loading and unloading[J]. Rock and Soil Mechanics, 2009, 30(12): 3562−3567.
[17] 丁发兴, 余志武. 基于损伤泊松比的混凝土多轴强度准则[J]. 固体力学学报, 2007, 28(1): 13−19. DING Faxing, YU Zhiwu. Strength criterion for plain concrete under multiaxial stress states based on damage Poisson‘ ratio[J]. Acta Mechanica Solida Sinica, 2007, 28(1): 13−19.
[18] 葛修润, 周百海, 刘明贵. 对岩石峰值后区特性的新见解[J]. 中国矿业, 1992, 1(2): 57−60. GE Xiurun, ZHOU Baihai, LIU Minggui. A new understanding of post-failure behaviour of rock[J]. China Mining Magazine, 1992, 1(2): 57−60.
[19] 朱传云, 喻胜春. 爆破引起岩体损伤的判别方法研究[J]. 工程爆破, 2001, 7(1): 12−16. ZHU Chuanyun, YU Shengchun. Study on the criterion of rockmass damage caused by blasting[J]. Engineering Blasting, 2001, 7(1): 12−16.
(编辑 陈灿华)
Influences of initial damage on mechanics of brittle rock under compressed stress
CHEN Leqiu1, 2, ZHANG Jiasheng1, CHEN Junhua1, CHEN Jiguang2
(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Department of Construction & Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China)
The initial damage definition for rock and the method were presented based on current isotropic damage constitutive model. The initial damage was expressed as the inferiority degree of the initial modulus of rock compared with the undamaged modulus. The uniaxial compressive tests for basalt with different initial damages were carried out. The influences of initial damage of rock on the relationship among the uniaxial compressive stress and the uniaxial compressive strain, the uniaxial compressive strength, the failure strain, the initial value of Poisson's ratio, the strain softening, and so on, were quantitatively analyzed. The rule and fitting formula about the mechanical parameters (including the change of the uniaxial compressive strength, the initial Poisson ratio, and so on) changing with the initial damage of rock were presented. The results show that only their initial damage value surpasses the damage thresholdvalue which is corresponding to the peak stress of undamaged rock under uniaxial compressive loading, and the uniaxial compressive strength of initial damage rock samples decreases significantly with the increment of the initial damage. The strain corresponding to the peak stress increases almost linearly with the increment of the initial damage. The initial Poisson ratio shows exponential growth with the initial damage. The brittle failure after peak stress is remarkable with the decrement of the initial damage of rock.
rock; damage; uniaxial compressive strength; elastic modulus; brittle failure
10.11817/j.issn.1672−7207.2017.02.028
TU45
A
1672−7207(2017)02−0484−07
2016−05−29;
2016−07−22
国家自然科学基金资助项目(51308210)(Project(51308210) supported by the National Natural Science Foundation of China)
陈积光,教授,从事结构力学研究;E-mail:852679209@qq.com

