基于遗传算法带约束的翼伞系统归航轨迹设计

陶金，孙青林，朱二琳，陈增强，贺应平



基于遗传算法带约束的翼伞系统归航轨迹设计

陶金1，孙青林1，朱二琳1，陈增强1，贺应平2

(1. 南开大学计算机与控制工程学院，天津，300350；2. 中航工业宇航救生装备有限公司，湖北襄阳，441003)

翼伞系统归航轨迹设计是一类带约束的最优控制问题，引入一种具有精英策略的遗传算法解决此类问题。为方便使用遗传算法，引入非均匀B样条曲线拟合控制律，将最优控制问题转化为B样条基函数控制顶点的参数优化问题，并针对归航终端等式约束，引入松弛因子将其转化为不等式约束，进而采用静态罚函数法处理。在2种不同初始条件下的归一化模型中进行仿真，并针对实际工程中着陆精度要求设定3种不同的松弛因子。仿真结果表明：使用本文的方法解算出的归航轨迹及其控制信息合理，是符合工程实际需求的一种有效方法。

翼伞系统；归航轨迹优化；遗传算法；罚函数；约束处理；松弛因子

翼伞系统[1]归航轨迹设计是指给定起始点和目标点，在特定的动力学约束基础上，规划1条满足特定性能指标的最优路径。传统的最优归航轨迹设计方法是基于控制论的优化算法，主要分为间接法和直接法。间接法是通过由变分法或庞特里亚金极大值原理得到的最优条件来求解最优归航轨迹。比较有代表性的研究成果有熊菁[2]运用极小值原理将归航轨迹规划的最优控制问题转化为两点边值问题，然后采用共轭梯度法进行求解；SLEGERS等[3]将翼伞系统归航中最后阶段(逆风对准) 的最优控制问题转化成两点边值问题求解。由于间接法求解过程比较繁琐，因此，在进行翼伞系统归航轨迹设计时，多采用直接方法求解。直接法是把含有性能指标的最优控制问题转化为非线性规划问题进行归航轨迹设计。比较有代表性的研究成果有ZHANG等[4−5]使用高斯伪谱法将翼伞系统归航轨迹离散处理转化为具有一系列代数约束的大规模非线性优化问题，并用二次规划方法进行求解；CLEMINSON等[6]采用动态规划法对翼伞系统自动归航路径进行了研究。但无论是间接法还是直接法，由于都是采用传统的基于梯度的搜索方法，因此，对初值十分敏感，优化结果在很大程度上取决于对初始值的猜测，因而限制了其在工程上的应用。近年来，随着计算机技术的发展，涌现出大批新型的智能进化算法。这些算法具有较强的鲁棒性和广泛的适应性，对初始值不敏感，以高效、实用的特点吸引着学者尝试用于解决翼伞系统归航轨迹设计问题。比较有代表性的研究成果有LIU等[7−8]采用改进的粒子群算法寻优得到了基于最优控制的翼伞系统归航轨迹的近似最优解；焦亮等[9]使用混沌粒子群算法对灾难环境下翼伞空投机器人系统轨迹进行了规划。以上工作对于问题的求解多是将翼伞系统归航轨迹设计问题视为一类多目标优化问题，使用权重因子的方法将多目标优化转化为单目标优化，然后进行单目标函数寻优，优化结果严重依赖于权重因子的选择。其他关于翼伞系统轨迹规划的研究成果有：ROSICH等[10]对翼伞系统的群体归航的轨迹及控制规则进行了研究；LUDERS等[11]提出了一种基于快速扩展随机树的在线规划算法，在任意非凸的绘制地图上实现了翼伞系统风扰下精确归航的无碰路径生成；LEE等[12]提出了1种两点边值贝叶斯曲线轨迹规划方案；JONATHAN等[13]针对翼伞系统归航过程中易受风影响的问题提出了1种选择性轨迹规划方式来确定所跟踪的预定轨迹。与上述的大部分研究工作不同的是，本文作者将翼伞系统归航轨迹设计问题归纳为一类具有约束的最优控制问题，采用1种具有精英策略的遗传算法进行归航轨迹寻优，解决传统方法初始值难以估计的问题；将着陆距离偏差和逆风对准两项归航指标视为控制约束，对单一能耗目标函数进行优化，且引入带松弛因子的静态罚函数法处理约束，松弛因子可以根据不同工程实际需求进行设定，减少了加权因子选择的困难，也使规划结果可控，且更加符合工程实际需求。

1 最优控制问题描述

翼伞系统归航轨迹设计问题的本质是一类非线性，带有状态约束、控制约束和终端约束的最优控制问题，从以下4个方面进行阐述。

1.1 系统数学模型

翼伞系统动力学模型复杂，非线性强，耦合多，因此，在翼伞系统归航轨迹规划中通常采用相对简单的质点模型，以简化计算。本文通过对文献[14]中的全展开翼伞系统六自由度运动模型进行仿真，并进行一定的假设简化，提炼出翼伞系统质点模型的运动方程，用来代替复杂的高自由度模型进行归航轨迹的最优设计。

翼伞系统质点模型归航轨迹设计通常采用风坐标系，风坐标系中各坐标轴的方向与大地坐标系一致，但其坐标原点随着气流而运动。这样可以将风的大小、方向以及系统随高度的变化等影响都转化到起始点的位置偏移中。由于翼伞系统的飞行控制是通过左右电机带动绞盘上缠绕的翼伞后缘两侧的操纵绳来实现的，无论是单侧下偏操作还是双侧下偏操作，当下偏量在能够维持翼伞系统稳定飞行范围内波动时，其水平飞行速度和滑翔比变化很小，因此，进行以下假设，用来简化模型：

1) 在翼伞充满后完全展开的稳定飞行状态下，忽略大气密度变化和左右下偏操作对翼伞系统飞行速度的影响，认为其水平飞行速度和滑翔比保持不变。

2) 只考虑水平风场，且风向和风速是已知的，忽略风对翼伞系统姿态的影响。

3) 系统对控制输入的响应无延迟。

基于以上3点假设，在风坐标系之上，选取目标点(设定为翼伞系统开始实施雀降着陆时的坐标点)为坐标原点，翼伞系统的运动方程可以简化为

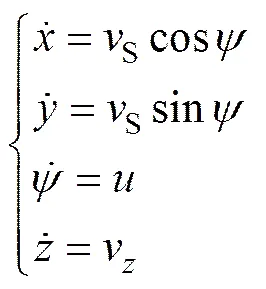
其中：，和分别为翼伞系统在风坐标系轴、轴和轴的坐标信息；S为翼伞系统水平飞行速度；v为垂直下落速度；为偏航角；为偏航角速率；为控制量；与偏航角速率(即翼伞系统操纵绳的单侧下偏量)存在一一对应的关系。

1.2 边界条件与目标集

基于上述的假设条件和质点模型，在翼伞系统归航轨迹设计问题中，初始时刻、初始状态及末端时刻、末端状态都是已知和固定的。将边界条件和目标集概括如下。

1.2.1 初始状态

翼伞系统归航的初始时间为0，则其初始条件可以表述为

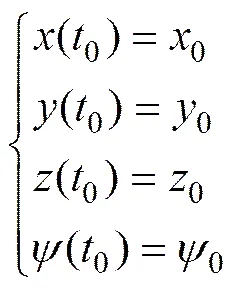
式中：0，0和0为起始时刻翼伞系统坐标信息；0为起始时刻偏航角。

1.2.2 终端约束

翼伞系统归航的终止时间为f，则f=0/v，终端状态可以表述为

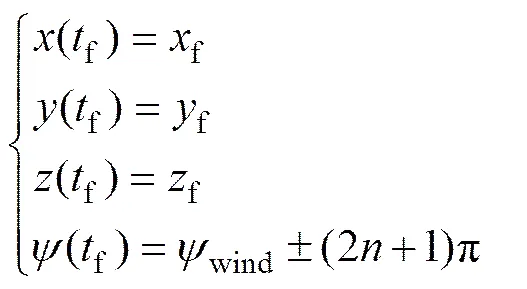
式中：f，f和f为着陆点坐标信息，wind为水平风向，着陆方向wind(f)与wind的偏差为±(2+1)π，是为保证翼伞系统着陆时刻逆风。

1.3 容许控制

容许控制表示如下：

式中：为控制域，其取值范围为[−max，max]，max为允许输入的最大控制量，与翼伞系统最小转弯半径相对应。

1.4 性能指标

翼伞系统归航所需满足的条件可以归纳如下。

1) 着陆点距离目标点近。

2) 逆风着陆。这是翼伞系统实施雀降的必要条件，通过雀降可以减小翼伞系统着陆时的速度，避免着陆过程中对回收物造成损伤。

3) 能耗少。这要求归航控制过程中电机消耗的能量越少越好。

根据翼伞系统归航所需满足的条件，选取条件(3)最小能量消耗作为最优控制问题性能指标：

条件1)和2)则视为翼伞系统归航最优控制问题约束条件，表示为

(6)

式中：约束条件1()=0表示终端时刻着陆点与目标点偏差为0，即在目标点着陆；2()=0表示着陆时刻航向角(f)与风向wind偏差为±(2+1)π，即逆风着陆。

根据上述翼伞系统归航最优控制问题基本组成部分，归纳一般提法为：在满足系统运动方程(1)的约束条件下，在容许控制域(4)中确定1个最优控制律*，使系统状态从初始状态(2)转移到要求的目标集合(3)，满足约束条件(6)，并使性能指标(5)达到最优。这是一类典型Lagrange型最优控制问题，进一步描述为翼伞系统归航过程中用较少的能耗使得终端时刻着陆点与目标点偏差在要求范围内且符合逆风着陆条件。其等效的优化问题模型为

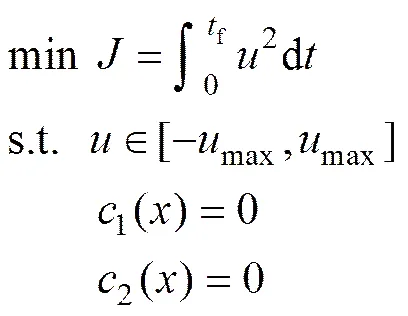
2 基于遗传算法的归航轨迹设计

针对所述的带有约束的最优控制问题，采用类具有精英策略的遗传算法进行解算。首先将各变量归一化处理以提高求解问题的精度；引入非均匀B样条技术进行控制律的拟合以实现参数化；约束条件采用带松弛因子的静态罚函数法进行处理。

2.1 归一化处理

在翼伞系统归航轨迹优化过程中，由于状态变量的量级相差较大，在轨迹积分的过程中会导致有效位数的损失，归一化处理可以有效克服这一问题，提高计算精度。另外，对归航轨迹的优化也要求优化变量尽可能地保持在相同的量级，故作以下处理，令

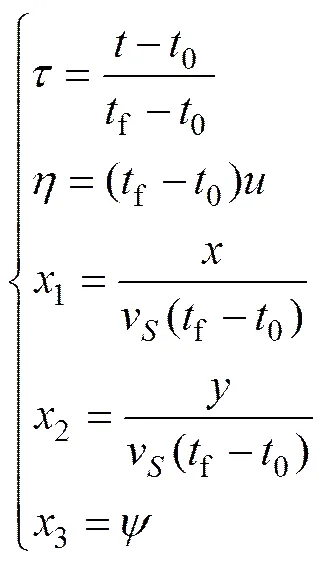
则运动方程式(1)转化为

(9)

初始状态式(2)转化为

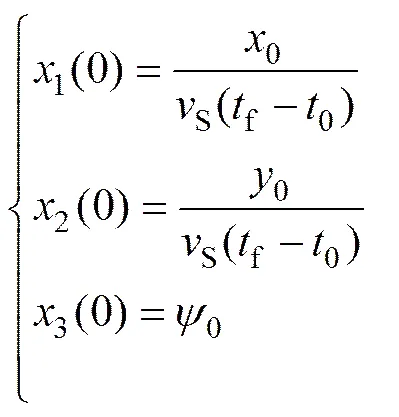
终端约束式(3)转化为

(11)

容许控制式(4)转化为

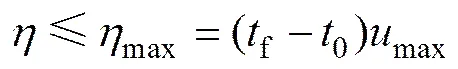
约束条件式(6)转化为

(13)

等效的优化问题描述式(7)转化为

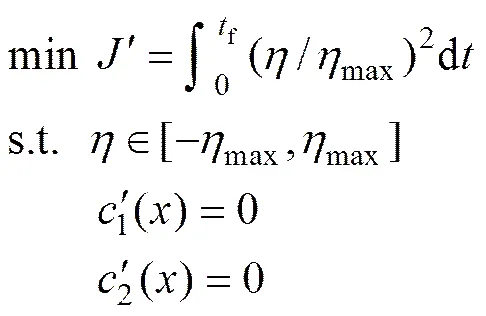
2.2 参数化方法

翼伞系统归航轨迹的优化空间是泛函空间，使用遗传算法不能直接进行解算，因此首先要将最优控制问题转化为参数优化问题。常用的参数化方法主要有直接离散法、多重参数插值法和函数逼近法。本文为简化编码及计算的复杂度，考虑到翼伞系统控制量必须是连续的，采用非均匀B样条技术[9,15]逼近控制率的方法来实现参数化。非均匀B样条拟合曲线定义如下：

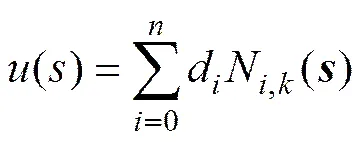
式中：d为第个控制顶点；N,k()为由节点矢量= [0，1，…，s+k+1]决定的次B样条基函数；=0，1，…，，本文中采用德布尔−考克斯递推方法得到。次B样条基函数的支撑区间为[s，s+k+1]，包含+1个节点区间，节点矢量可采用哈特利−贾德公式来确定。按照上述方法对控制变量进行编码。根据式(15)，给出若干控制定点d，为控制顶点的个数。一般来讲，控制点个数越多，所描述的控制规律越精确，但无疑又会增加相应计算量，本文中选用7个控制顶点，基函数选取常用的3次非均匀B样条曲线。

2.3 约束条件处理

使用遗传算法对问题目标进行优化必须对约束条件进行处理，但目前来讲，还没有处理约束的一般性方法，通常的处理方法有搜索空间限定法、可行解变换法和罚函数法。对于轨迹优化问题，罚函数法是一种有效方法。本文中引入松弛因子将终端等式约束转化为不等式约束，进而采用一种简单的静态罚函数法进行处理。引入松弛因子1和2，约束条件式(13)可化为

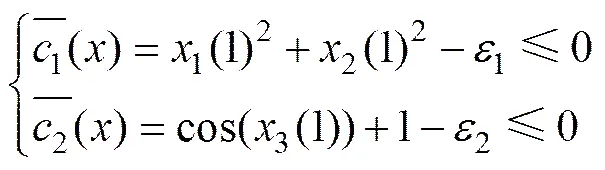
(17)

式中：1和2为惩罚函数系数，其值的选取要度量解对约束条件的不满足程度和计算效率，用以调整惩罚函数惩罚度，本文选取1=1，2=0.3。由上述可知：当满足约束条件时，；当不满足约束条件时时，，增加相应惩罚，使得解个体向着满足约束的方向进化。

2.4 遗传算法设计

文章的结尾也很重要，既不能有头无尾，又不能虎头蛇尾，或画蛇添足。初中语文教材课文中的结尾有以下几种常用的，可供我们写作时借鉴。

本文采用一种具有精英策略的遗传算法解决这类带约束的翼伞系统归航轨迹设计的最优控制问 题[16−19]。与传统的遗传算法不同，本算法中引入交叉后代比例的概念，表示子代中由交叉产生的个体父代中非精英个体数的比例，其值是1个0~1的数。所采用的精英策略是指父代中的精英个体原封不动地直接传给子代，而不经过交叉和变异操作。采用精英策略的优势在于：在进化过程中，种群中的最优个体不会因为选择、交叉和变异操作而破坏或丢失，对改善遗传算法的收敛性有重要作用。RUDOLPH[19]使用有限齐次马尔科夫链证明了仅采用选择、交叉和变异的经典遗传算法无法收敛到全局最优，而具有精英策略的遗传算法是全局收敛的。本文中精英策略的具体操作为将保留的精英个体直接替换子代中适应度最低的相同数目的个体，从而保证种群规模的一致性。

本文中采用实数编码，编码方法采用非均匀B样条技术，B样条基函数的控制顶点即组成了遗传空间染色体上的基因。种群规模取为100，精英个体数目取为20，迭代次数取为200，交叉后代比例取为0.75.

3 仿真算例与分析

3.1 仿真条件

作为仿真实例，本文选用空投质量w=80 kg的伞型，翼伞展弦比=1.73，伞绳长度l=3.7 m，吊带长度w=0.5 m，伞衣面积p=22 m2，空头物阻力特征面积w=0.5 m2，安装角=7°。根据所选的伞型及其六自由度仿真结果，在保证翼伞系统倾斜角小于20°的前提下，翼伞系统基本运动参数为：初始速度s=15 m/s，v=5 m/s，电机控制量max=30，翼伞系统空投初始高度=2 000 m。

3.2 仿真结果及分析

为了全面分析翼伞系统归航轨迹的形态、控制特点以及松弛因子选择对归航轨迹规划结果的影响，以下取2种初始运动状态，分别为初始状态：1(0)=0.5，2(0)=0，3(0)=−π/3；初始状态：1(0)=0.6，2(0)=0.6，3(0)=π；其对应风坐标系下实际坐标位置分别为初始状态：0=3 000 m，0=0 m，0=60°；初始状态：0=3 600 m，0=3 600 m，0=180°。考虑到3种工程实际翼伞系统归航着陆精度设计要求，设定3种松弛因子方案，如表1所示。比如方案2归航着陆精度要求为着陆点距离目标点偏差在6 m之内，着陆点方向与水平风向夹角大于等于172°。根据式(8)和(16)进行推算，松弛因子1和2可设置为：

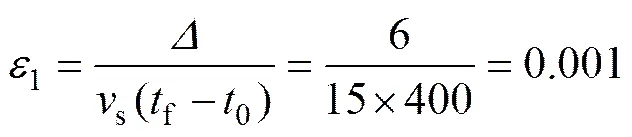
采用本文提及的方法，分别在初始状态和下，采用3种松弛因子设定方案进行翼伞系统归航轨迹最优设计，并在Matlab上进行仿真分析。

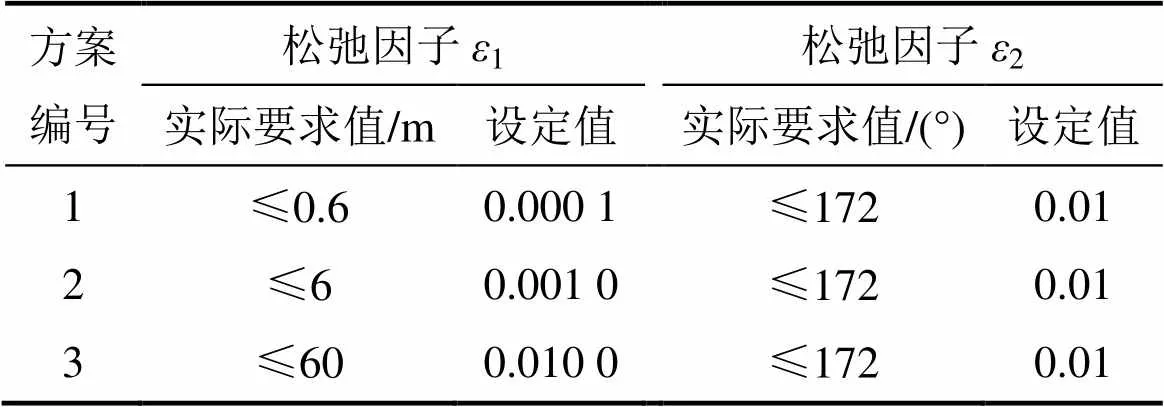
表1 3种松弛因子设定方案

图1所示为带精英策略的遗传算法的最优适应度值迭代曲线。从图1可以看出：在精英策略的作用下，算法表现出良好的收敛性能，在第8代附近已基本接近最优值，获得最优解的平均CPU时间小于2 s，符合翼伞系统实际工程控制需求。图2所示为翼伞系统在初始状态下，采用3种松弛因子设定方案的归航轨迹及其对应控制曲线。图3所示为翼伞系统在初始状态下，采用3种松弛因子设定方案的归航轨迹及其对应控制曲线。

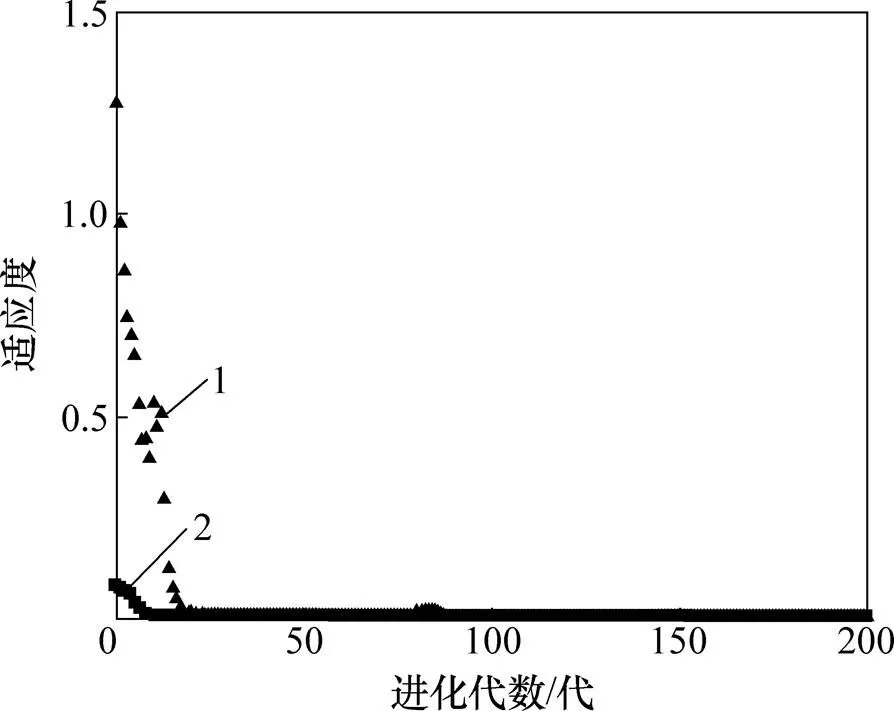
1—平均适应度；2—最优适应度。

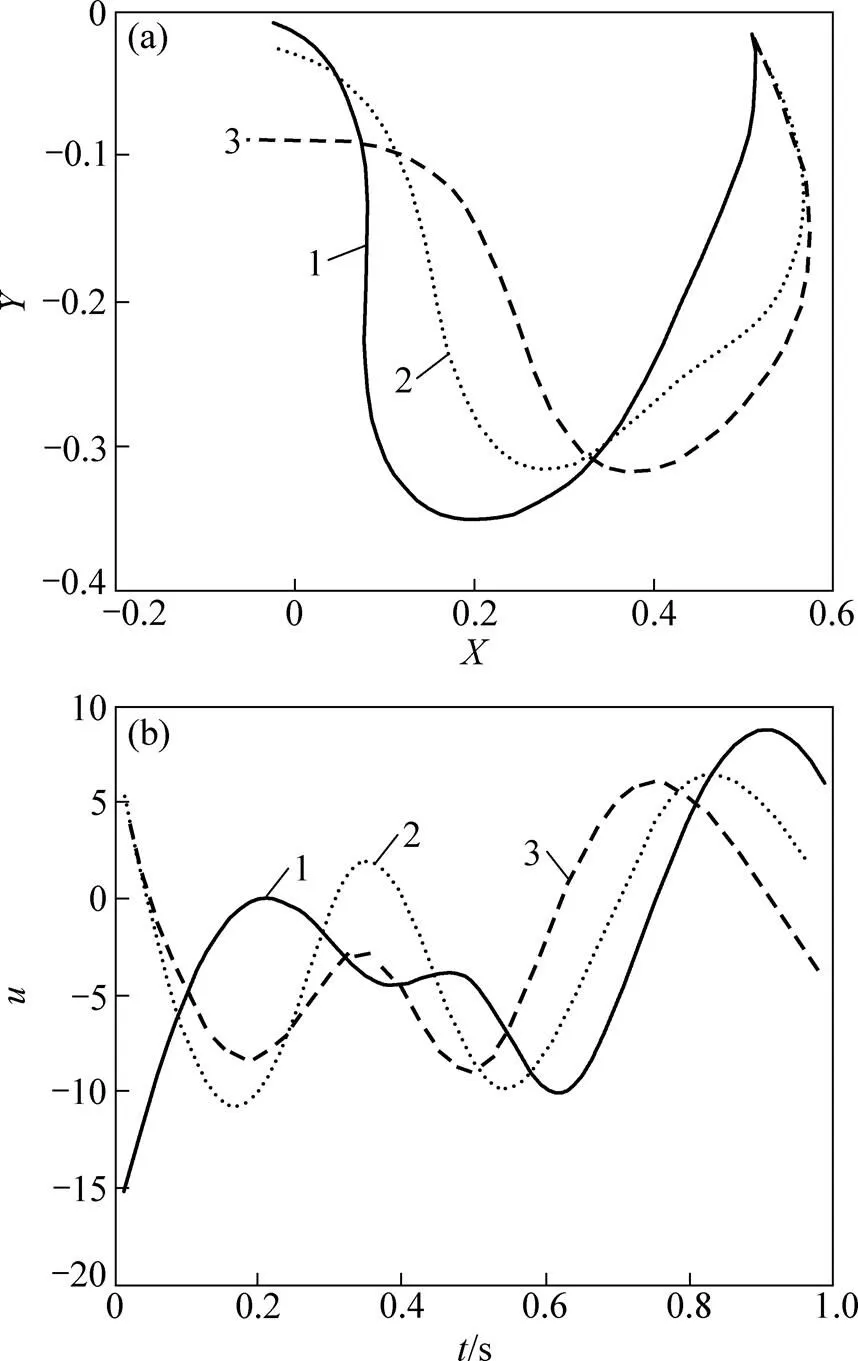
(a) X−Y平面归航轨迹；(b) 控制曲线

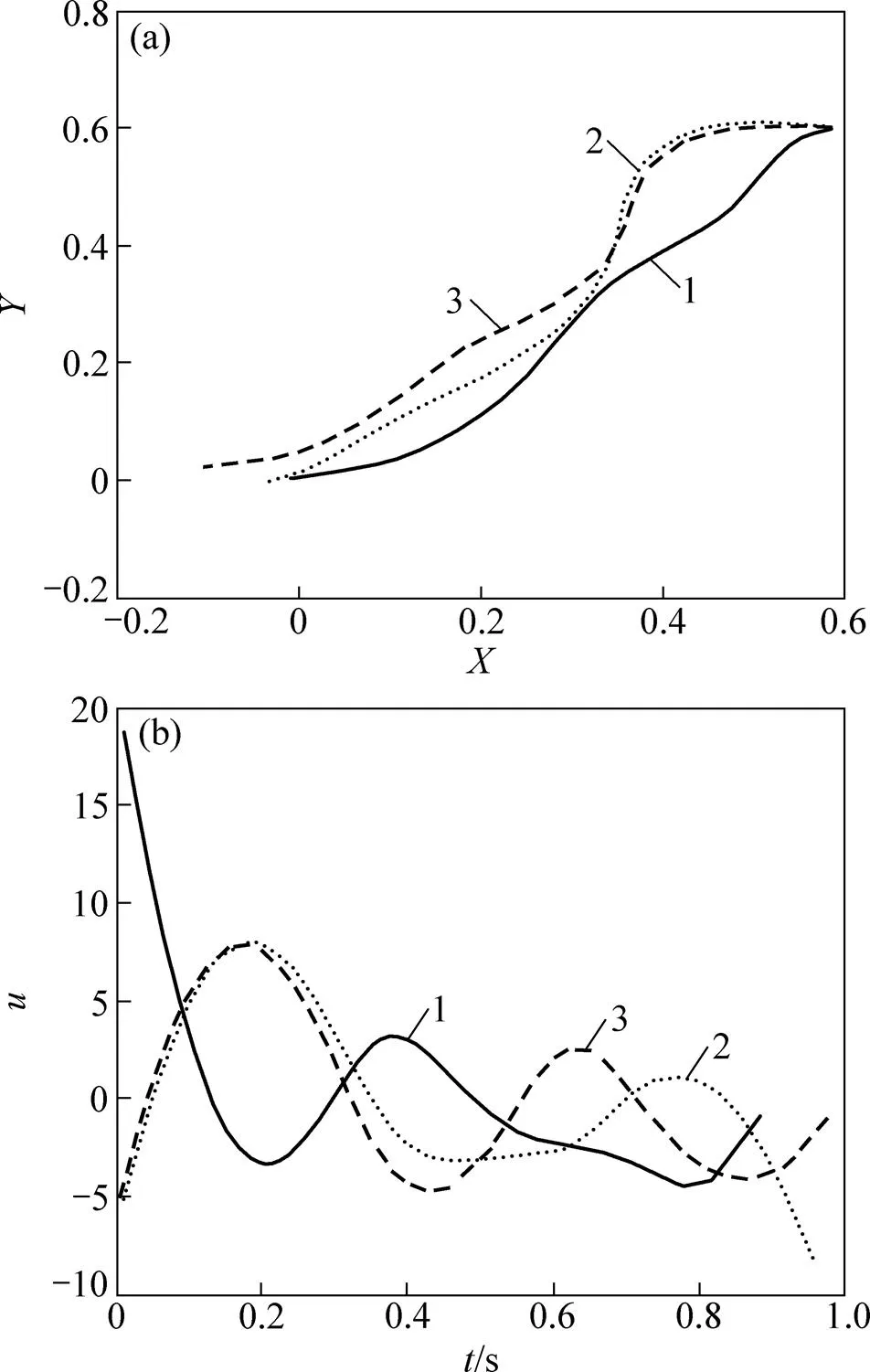
(a) X−Y平面归航轨迹；(b)控制曲线

表2给出的是翼伞系统在初始状态和下分别采用3种松弛因子设定方案的最终归航结果。从表2可以看出：虽然初始状态距离目标点比初始状态要远，但是在相同松弛因子设定方案下，初始状态归航所需能耗要低于初始状态。这是由于翼伞系统在初始状态归航过程中较多的采用滑翔飞行，能量消耗相对较少。

从表2可知：在松弛因子较大即条件约束较宽松的情况下，如初始条件和下方案2和3的着陆距离偏差、着陆方向偏差以及方案1的方向偏差，最终规划结果完全符合并优于表1中所述设计要求。当松弛因子较小即约束严格的情况下，如方案1的距离偏差，结果虽然不能完全满足工程实际设计要求，但仍然在可接受的范围内。通过比较相同初始条件不同松弛因子设定方案下归航能耗，可以得出随着归航精度要求降低，即松弛因子1增大，能耗也相应减小，说明遗传算法在宽松约束条件下能够搜索出具有更为优秀性能指标的解。

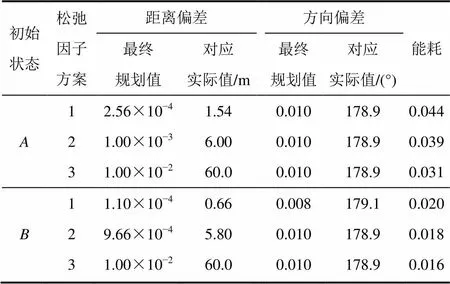
表2 归航结果

4 结论

1) 将各变量进行归一化处理，提高了求解问题的精度。

2) 采用非均匀B样条曲线拟合控制律，简化了编码，提高了控制律的表达能力，从而将动态最优控制问题转化成静态参数优化问题。

3) 针对终端等式约束，引入松弛因子将其转化为不等式约束，并采用静态罚函数法进行处理，且松弛因子可根据工程实际着陆点精度要求进行设定。

4) 引入一种具有精英策略的遗传算法解决此类问题，优化结果对初始值不敏感，具有较强的鲁棒性。

5) 提出的方法解算出的归航轨迹及其控制信息合理，规划结果可控，工程人员可针对不同工程实际归航精度设计要求设定松弛因子，以取得符合设计要求的翼伞系统归航控制律信息。该方法为解决翼伞系统归航轨迹优化的问题探索出了一条新路径。

[1] 李春, 吕智慧, 黄伟, 等. 精确定点归航翼伞控制系统的研究[J]. 中南大学学报(自然科学版), 2012, 43(4): 1331−1335.LI Chun, LÜ Zhihui, HUANG Wei, et al. Guidance navigation & control system for precision fix-point homing parafoil[J]. Journal of Central South University(Science and Technology), 2012, 43(4): 1331−1335.

[2] 熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科技大学, 2005: 72−85.XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005: 72−85.

[3] SLEGERS N, YAKIMENKO O. Optimal control for terminal guidance of autonomous parafoils[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston, VA, USA: AIAA, 2009: 2958−2978.

[4] ZHANG Limin, GAO Haitao, CHEN Zengqiang, et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J]. Nonlinear Dynamics, 2013, 72(1/2): 1−8.

[5] 高海涛, 张利民, 孙青林, 等. 基于伪谱法的翼伞系统归航轨迹容错设计[J]. 控制理论与应用, 2013, 30(6): 702−708.GAO Haitao, ZHANG Limin, SUN Qinglin, et al. Fault-tolerance design of homing trajectory for parafoil system based on pseudo-spectral method[J]. Control Theory & Applications, 2013, 30(6): 702−708.

[6] CLEMINSON J R. Path planning for guided parafoils: An alternative dynamic programming formulation[C]//Proceedings of the 22nd AIAA Aerodynamic Decelerator Systems (ADS) Conference. Daytona Beach, FL, USA: AIAA, 2013: 2013−1346.

[7] LIU Zhao, KONG Jianyi. Path planning of parafoil System based on particle swarm optimization[C]//2009 International Conference on Computational Intelligence and Natural Computing. Piscataway, NJ, USA: IEEE, 2009: 450−453.

[8] 徐剑, 周德云. 基于最优控制的翼伞路径规划[J]. 火力与指挥控制, 2010, 35(10): 59−61. XU Jian, ZHOU Deyun. A path planning of parafoil system based on optimal control[J]. Fire Control and Command Control, 2010, 35(10): 59−61.

[9] 焦亮, 孙青林, 亢晓峰. 基于混沌粒子群优化算法的翼伞系统轨迹规划[J]. 复杂系统与复杂性科学, 2012, 9(1): 47−54.JIAO Liang, SUN Qinglin, KANG Xiaofeng. Route planning for parafoil system based on chaotic particle swarm optimization[J]. Complex Systems and Complexity Science, 2012, 9(1): 47−54.

[10] ROSICH A, GURFIL P. Couling in-flight trajectory planning and flocking for multiple autonomous parafoils[J]. Journal of Aerospace Engineering, 2012, 226(6): 691−720.

[11] LUDERS B, SUGEL I, HOW J P. Robust Trajectory Planning for Autonomous Parafoils under Wind Uncertainty[C]//Aemerican Institute of Aeronautics and Astronautic Conference. Reston, VA, USA: AIAA, 2013: 1−27.

[12] LEE F, JONATHAN R. Bézier curve path planning for parafoil terminal guidance[C]//Proceedings of the 22nd AIAA Aerodynamic Decelerator Systems(ADS) Conference. Reston, VA, USA: AIAA, 2013: 2013−1325.

[13] JONATHAN R, NATHAN S. Robust parafoil terminal guidance using massively parallel processing. Journal of Guidance[J]. Control and Dynamics, 2013, 36(5): 1336−1345.

[14] JIAO Liang, SUN Qinglin, KANG Xiaofeng, et al. Autonomous Homing of Parafoil and Payload System Based on ADRC[J]. Journal of Control Engineering and Applied Informatics, 2011, 13(3): 25−31.

[15] BELAIDI H, HENTOUT A, BOUZOUIA B, et al. NURBS trajectory generation and following by an autonomous mobile robot navigating in 3D environment[C]//2014 IEEE 4th Annual International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER). Pisctaway, NJ, USA: IEEE, 2014: 168−173.

[16] 刘扬, 鲁乃唯, 殷新锋. 基于体系可靠度的钢桁梁结构优化设计[J]. 中南大学学报(自然科学版), 2014, 45(10): 3629−3636.LIU Yang, LU Naiwei, YIN Xinfeng. Structural optimization design of steel truss beam based onsystem reliability[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 1331−1335.

[17] 陈曦, 谭冠政, 江斌. 基于免疫遗传算法的移动机器人实时最优路径规划[J].中南大学学报(自然科学版), 2008, 39(3): 577−583.CHEN Xi, TAN Guanzheng, JIANG Bin. Real-time optimal path planning for mobile robots based on immune genetic algorithm[J]. Journal of Central South University (Science and Technology), 2008, 39(3): 577−583.

[18] 雷英杰, 张善文. 遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社,2014:143−223.LEI Yingjie, ZHANG Shanwen. Genetic algorithm toolbox and its application[M]. Xi’an: Xi’an Universityof Electronic Science and Technology Press, 2014: 143−223.

[19] RUDOLPH G. Convergence analysis of canonical genetic algorithms[J]. IEEE Trans on Neural Networks, 1994, 5(1): 96−101.

(编辑 陈爱华)

Genetic algorithm based homing trajectory planning of parafoil system with constraints

TAO Jin1, SUN Qinling1, ZHU Erlin1, CHEN Zengqiang1, HE Yingping2

(1. College of Computer and Control Engineering, Nankai University, Tianjin 300071, China;2. Aerospace Life-Support Industries Ltd,Aviation Industry Corporation of China, Xiangyang 441003, China)

Homing trajectory planning of parafoil system is a kind of optimal control problem with constraints, a kind of genetic algorithm with elite strategy to solve such a problem was introduced. For the convenience of using genetic algorithm, the non-uniform B-spline was adopted to characterize the control law, so as to transform the optimal control problem into a control vertices of B-spline basis function optimization problem. In view of homing terminal equality constraints which can be converted into inequality constraints by relaxation factors, a static penalty function method was introduced. The normalized model under two different initial conditions was simulated, and three kinds of relaxation factors were set according to landing accuracy requirements of practical engineering. The simulation results show that the control information of homing trajectory is reasonable, and it is an effective method which is suitable for practical engineering demands.

parafoil system; homing trajectory planning; genetic algorithm; penalty function; constraints handling; relaxation factor

10.11817/j.issn.1672−7207.2017.02.019

V249；TP13

A

1672−7207(2017)02−0404−07

2016−04−11；

2016−06−29

国家自然科学基金资助项目(61273138)；天津市重点基金资助项目(14JC2DJC39300)(Project(61273138) supported by the National Natural Science Foundation of China; Project(14JC2DJC39300) supported by the Key Fund of Tianjin Municipal)

孙青林，教授，博士生导师，博士，从事自适应控制、嵌入式控制系统和柔翼无人机导航、制导和控制等方面的研究；E-mail：sunql@nankai.edu.cn