深埋高侧压巷道底鼓机理分析及控制

曹平，李好月，钟涌芳，王飞



深埋高侧压巷道底鼓机理分析及控制

曹平，李好月，钟涌芳，王飞

(中南大学资源与安全工程学院，湖南长沙，410083)

通过理论分析、数值计算、力学推导、现场试验等方法，完成深部不同侧压下的巷道底鼓过程模拟，研究高侧压巷道的底板变形规律，进行巷道底板与钢管梁共同作用的机理分析及模型转换计算，实现多梁联合控制底鼓设计方案的验证。研究结果表明：底板两侧受高水平应力的作用向裸露面发生弯曲，其过程分为加速形变、匀速形变、过渡形变和最终稳定4个阶段；随侧压系数增大，底鼓现象加重，当0.5＜＜1.5时，变化尤为明显，当＞2.0时，变化速率减缓，但仍呈增加趋势；采用钢管梁横撑底板两帮，可减弱两帮向内收敛挤压底板的趋势，能提供横向支护反力以抵抗底板变形；沿巷道走向布置钢管梁，构成多梁联合控制体系，使单梁的控制范围实现区域重叠，可以增强底板整体抗弯曲变形能力。

采矿工程；侧压系数；巷道底鼓；底鼓控制

随着对能源需求量的增加和开采强度的不断加大，浅部资源日益匮乏，国内外矿山都相继进入深部资源开采状态[1]。巷道由于掘进或受回采影响引起其围岩应力状态发生变化以及在维护过程中围岩性质的变化，使顶底板和两帮岩体变形并向巷道内移动，底板向上隆起，这种现象称为底鼓[2]。研究表明[1−2]：进入深部开采后，底鼓量已占据巷道变形量的主要部 分[3]。底鼓导致巷道断面缩小，阻碍运输和人员行走，妨碍通风，甚至造成整个巷道报废，严重影响了矿山的生产和安全[4]。目前我国学者研究底鼓变形机理及控制的主要方式[2, 5−7]有：理论分析，数值模拟，相似材料实验，工程试验等。以产生的机理[2−3, 5−6, 8−9]为依据可将底鼓分为：挤压流动性底鼓，挠曲褶皱性底鼓，剪切错动性底鼓。巷道底鼓变形[2−5, 10]主要跟围岩应力，底板岩性，破碎程度，水理性质有关。目前使用的底板支护方式[11−15]有：底脚锚杆加固底板，“双壳”治理底鼓，加固顶板控制两帮，全长锚固、锚注加固底板，“切割槽”、“底板巷道”的泄压法等。地处高原地带的我国西北某金属矿山，目前开采深度已逾千米。矿区应力较高，且以水平应力为主：部分中段水平应力约为垂直应力的2倍甚至更高，巷道底板发生底鼓现象，影响巷道的运输、通风、供排水功能，缩短巷道服务年限，制约矿山的生产。

1 深部高侧压底鼓产生机制

当巷道位于矿山深部高侧压系数的应力场中，其受到的水平应力大于垂直应力，底脚部位发生应力集中现象，导致底板受到两帮的轴向挤压作用，沿其裸露面产生弯曲变形趋势。当水平应力增大到一定程度，底板开始向裸露面发生形变，从而产生底鼓。

将底板受水平应力挤压变形简化为受轴向力作用的板状材料力学模型，如图1所示。

底板压曲微分方程[16]为

式中：为弯曲刚度；为底板挠度；为中面应力。

应力表达式为

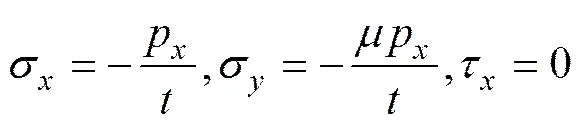
底板两侧中面应力为

(3)

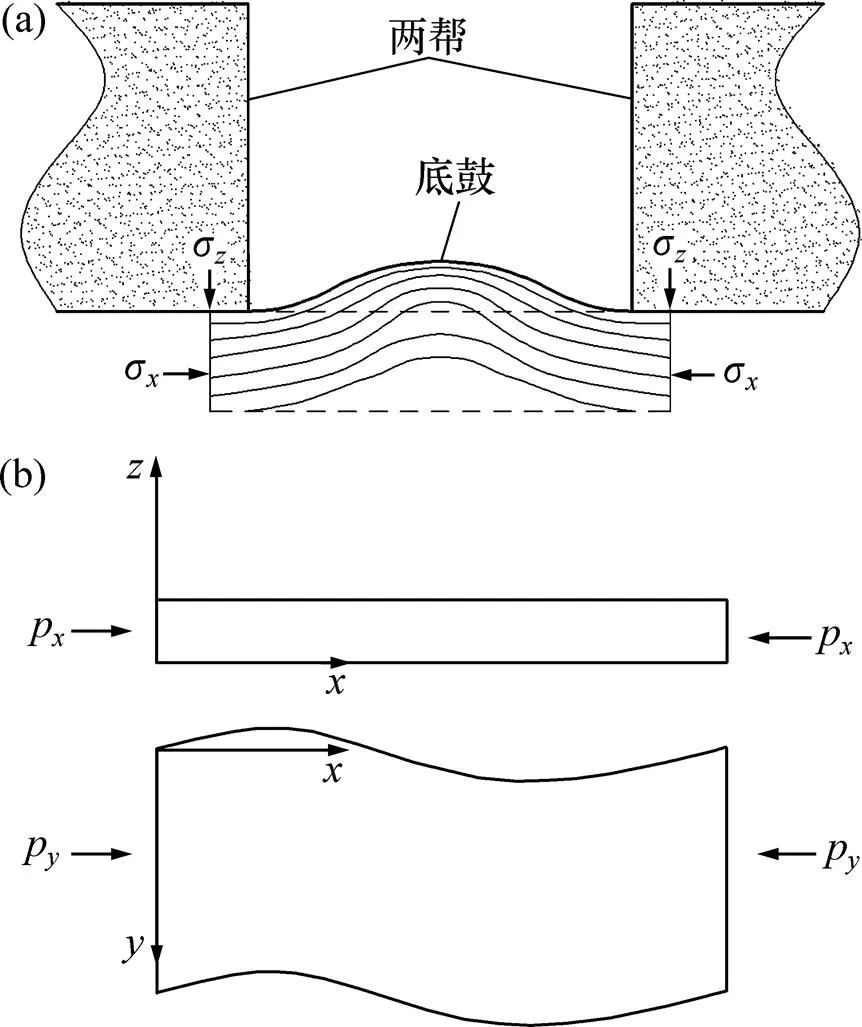
图1 底板弯曲

考虑仅与有关：

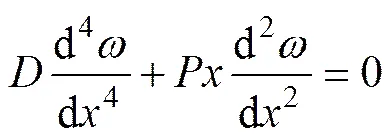
挠度表达式为

(5)

联立式(4)，底板压曲微分方程为

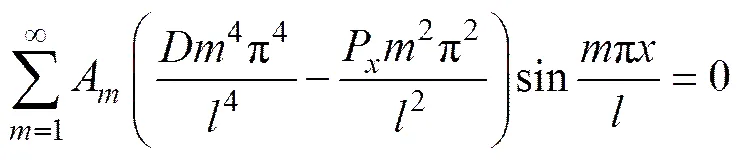
临界压曲条件为

(7)

令=1，解得临界面力(P)max为

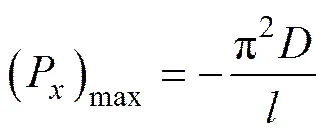
临界状态底板应力为

式中：为底板弯曲刚度；为变形厚度；为底板 长度。

当底板两侧面力P大于(P)max时，底板发生变形。

图2所示为底鼓量计算。底板鼓起量的一般估计为

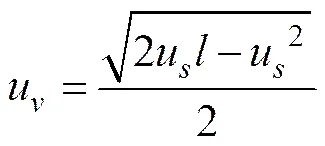
式中：为巷道端面宽度；u为两帮移近量；u为最大底鼓量。

图2 底鼓量计算

Fig. 2 Calculation of floor heave

2 高侧压底鼓过程模拟

2.1 计算模型

图3所示为计算模型。为提高模型创建和网格划分的效率[17]，利用AutoCAD的三维建模功能，并结合Midas/GTS强大的前处理能力，进行深部矿区开挖巷道三维模型的创建和实体网格的划分，完成后导入有限差分程序FLAC3D进行数值计算。模型尺寸50 m×30 m×20 m(长×宽×高)，共划分109 977个节点和101 760个单元。

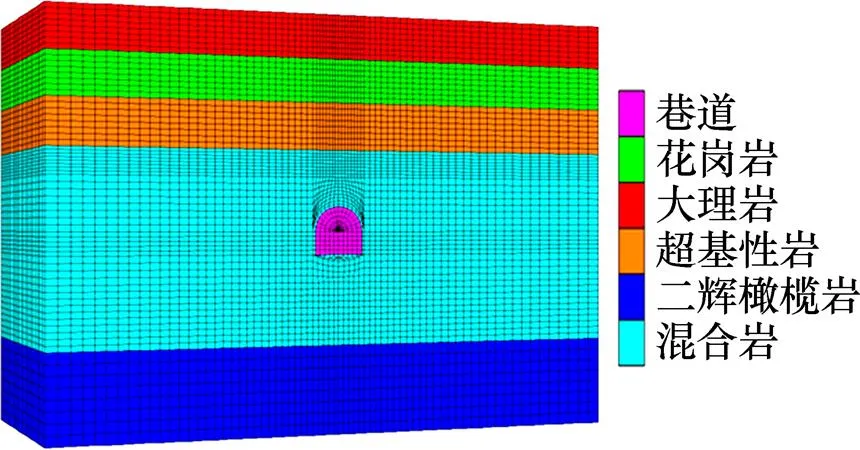
图3 计算模型

考虑岩石为脆性材料，在高地应力作用下表现为弹塑性变形状态，采用弹塑性本构模型，破坏准则采用摩尔−库仑准则[17]，施加位移边界条件。为研究不同侧压系数下深埋巷道的底板变形情况，运用S-B 法[18]，在相同垂直应力(实测垂直应力为27.6 MPa)的情况下，进行侧压系数分别为0.5，1.0，1.5，2.0，2.5和3.0时的初始地应力生成，各岩层物理力学参数见表1。

2.2 结果分析

不同侧压系数下深埋巷道底鼓量模拟结果如图4所示。结果表明：当侧压系数大于1.0时，巷道的破坏主要发生在顶底板方向；反之，则破坏主要发生在两帮方向，与文献[18]的理论分析结果一致。进一步整理巷道断面变形模拟数据，根据不同侧压系数下巷道底鼓量随时间变化的共性规律，绘制巷道底鼓量随时间的变化曲线如图5所示。图5显示：巷道开挖后，底板变形呈现非匀速变化过程，分为加速形变、匀速形变、过渡形变和最终稳定4个阶段，底板形变速率随时间的变化先增大后恒定最终减小为0。数值计算结果同时也显示：在巷道底板形变过程中，底板内部应力也随时间发生变化。在形变起始阶段，由于受到开挖影响，底板应力急剧增加；在匀速形变阶段，因受到巷道断面形变泄压的作用，底板应力保持恒定；在过渡形变和最终稳定阶段，应力呈几何减小状态，趋于向平衡发展。在围岩和应力的共同作用下，底板应力整体上属于先增后减的非匀速变化过程，最终完成应力二次平衡，实现应力重分布。

为消除因侧压增加对巷道底鼓量的影响，将底板底鼓量与顶板沉降量的比值/作为对比指标，以侧压系数为参照指标，根据计算监测记录，绘制不同侧压系数下巷道底鼓量与顶板沉降量的比值趋势，结果见图6。并进行数值拟合。研究发现：/随着侧压系数的增加而增大，且当0.5＜＜1.5时尤其明显；当＞2.0时，变化速率减缓，但仍呈增加趋势。此种情况说明当侧压系数增大时，巷道所处位置的水平应力与垂直应力的差值增加，呈现在巷道底板上的“挤压”作用愈加明显。受到两侧的“挤压”后，巷道底板向形变耗能最少的“裸露面”发生偏移，且考虑巷道两帮对底板两端在竖向位移上的限制作用，此时巷道底板则沿“裸露面”产生弯曲变形的趋势，进一步则发生底鼓现象。在实际的矿山工程当中，由于地质构造、应力场、温度场、渗流场及巷道布置、断面形状等的综合影响，底鼓现象更加严重[1−9]。

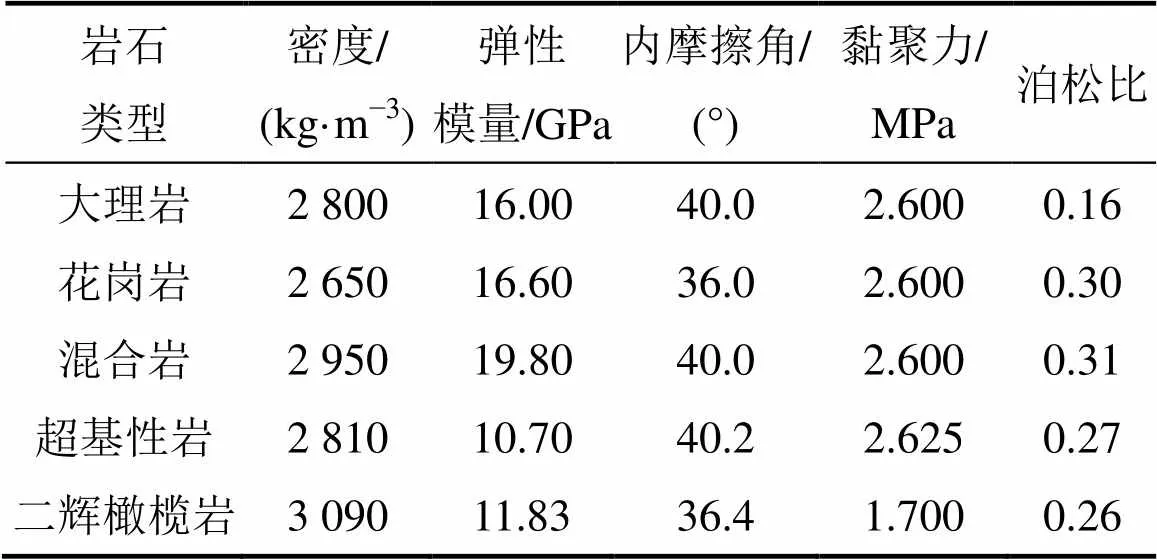
表1 岩层物理力学参数

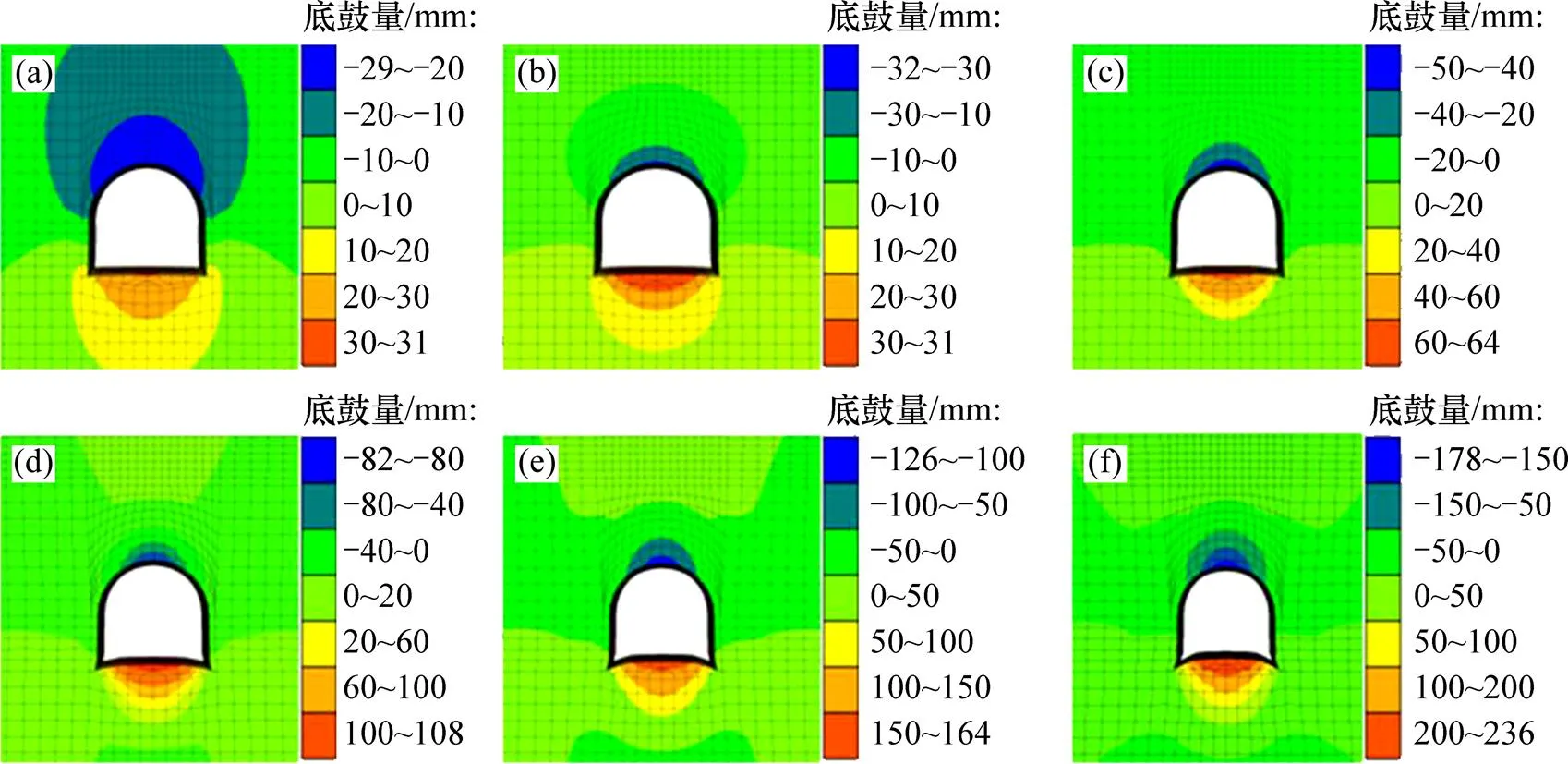
λ：(a) 0.5；(b) 1.0；(c) 1.5；(d) 2.0；(e) 2.5；(f) 3.0

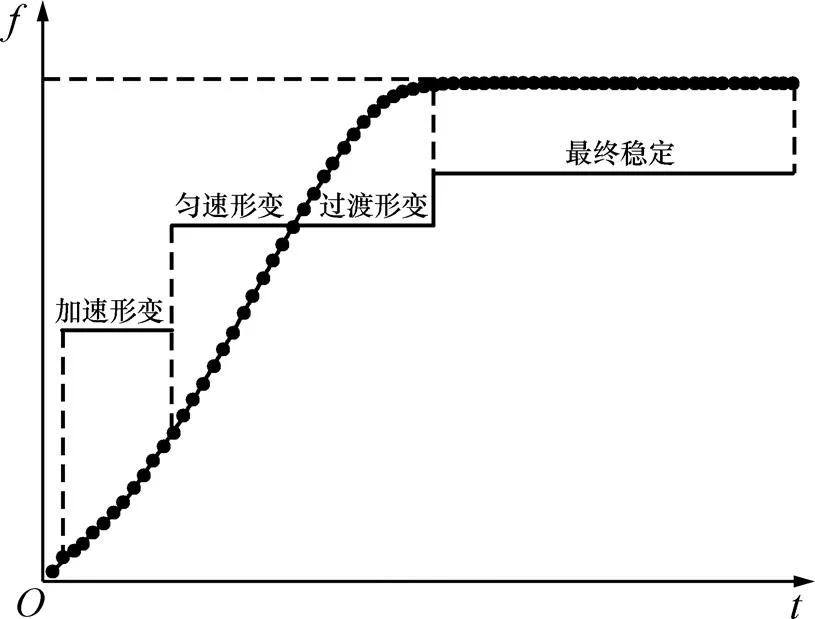
图5底鼓量f变化曲线

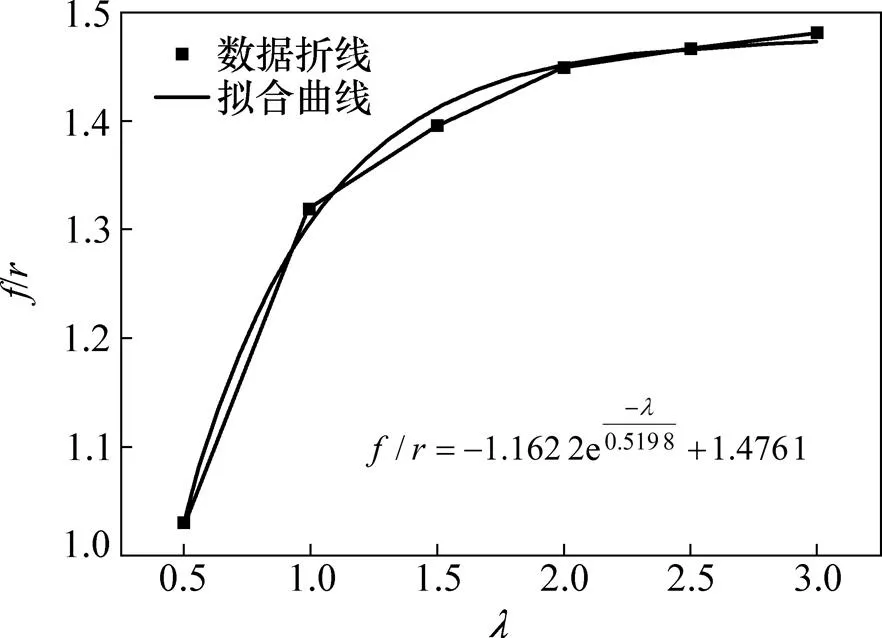
图6 f/r变化曲线

3 高侧压底鼓的控制方法

3.1 控制方法

由于高侧压系数下深埋巷道发生底鼓现象的根本原因是底板两侧受到高水平应力的挤压作用，因此，可通过减弱巷道两帮收敛趋势，增强底板抗弯曲变形能力的方式进行底鼓控制，必要时可钻打底脚长锚杆来阻断底脚的集中应力。鉴于钢管梁作为工程常用材料的易取性，以及其在承受轴向应力和横向荷载作用上的抗弯特性，设计多梁联合横撑底板两帮的控制底鼓支护方案，如图7所示。

为利用底板自身强度，先行释放一部分围岩应力，减弱两帮挤压作用对支护体的影响，于巷道底板开挖反拱槽。钢管梁在满足设计要求的情况下，具有足够的抗压强度和抗弯刚度。将其横置在预先开挖的底板反拱槽上，两端与巷道两帮接触，并沿巷道走向以间隔依次进行布置。支护完成后，钢管梁和底板围岩构成抵抗变形共同体，增强巷道底板在高水平应力挤压作用下的抗挠曲变形能力。其支护的力学机理主要表现为3个方面：依靠其轴向承载能力，撑住巷道两帮，减弱两帮向内收敛挤压底板的趋势；将底板的变形“裸露面”转换成抗弯刚度较高的支护载体即钢管梁，从而为抵抗底板弯曲变形提供足够的横向支护反力；沿巷道走向布置钢管梁，构成多梁联合控制支护体系，使单梁的控制范围实现区域重叠，增强底板整体抗弯曲变形能力。为了能够达到良好的支护效果，要求选择的钢管梁不仅要有足够的抵抗轴向应力变形的能力，而且应具有足够的抗弯刚度。

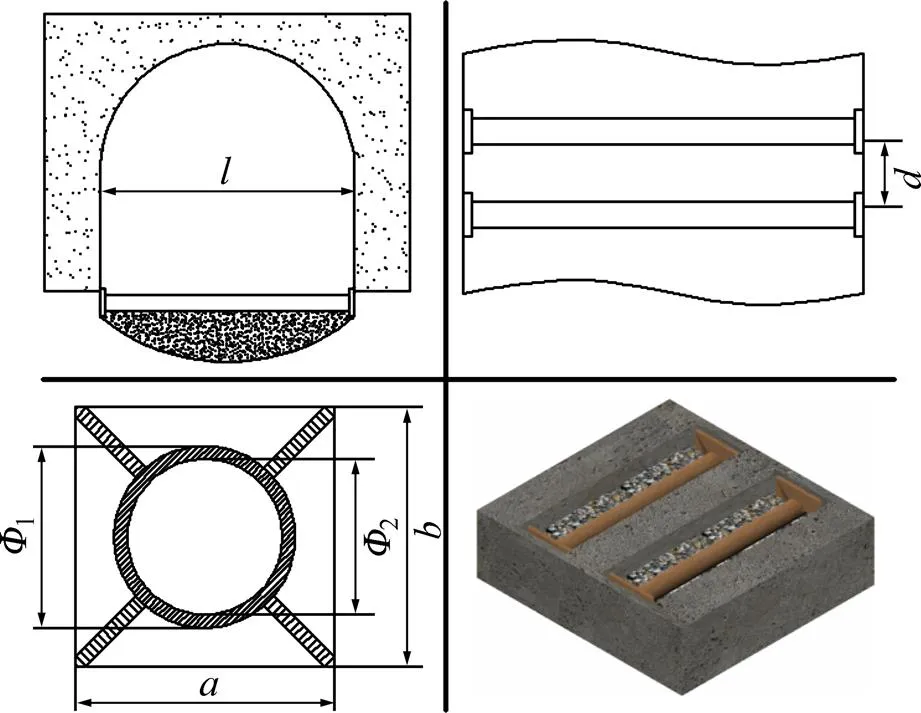
图7 钢管梁横撑支护

3.2 控制参数

多梁联合横撑底板两帮支护方案完成后，钢管梁与底板围岩形成抵抗变形共同体，在抵抗两帮轴向应力挤压作用的同时，在接触面上为底板提供横向抗弯支护反力，支护与底板共同受力如图8所示。

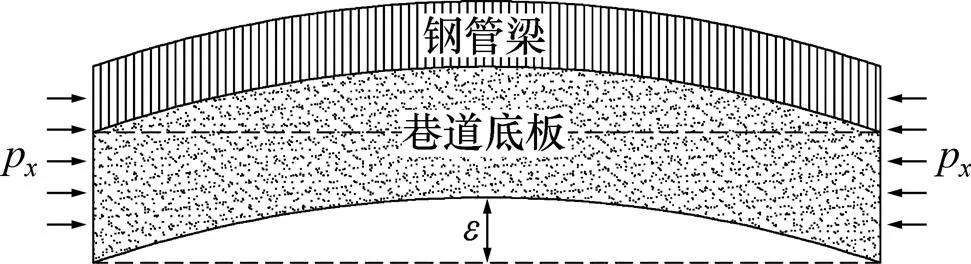
图8 钢管梁与底板共同作用

式(9)所示为巷道底鼓量的一般算式，可进行工程验算，但其仅是几何关系的推导，没有考虑力学特征。底板变形后，内部应力随之变化，但在微小形变内，仍属于弹性变形。为进行支护与围岩力学分析，在底板和钢管梁的弹性变形范围内：将巷道底板视作截面为矩形，受轴向荷载发生挠曲变形的弹性材料，挠度为；将钢管梁视作截面为圆环，受横向荷载发生挠曲变形的弹性材料，挠度为；假设钢管梁未脱离底板，2种材料在中部具有相等的最大挠度即max=max。

受轴向荷载下的材料(岩层)的挠度方程[16]为

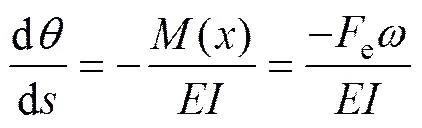
I为材料(岩层)的弯曲刚度，对取导数，有关系式，解得：

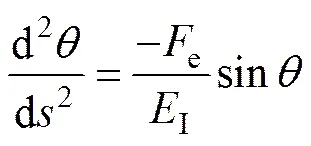
轴向荷载作用下的最大挠度max为

(12)

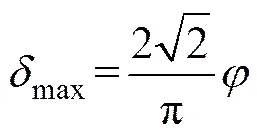
横向荷载材料(钢管梁)挠曲线近似方程为

(14)

式中：1为变形部位与梁端的长度，则横向荷载作用下的最大挠度为

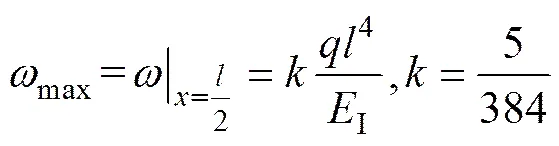
根据叠加原理，考虑max=max，可将轴向荷载与横向荷载进行等效转换，则

(16)

式中：为等效的均布荷载。

当钢管梁与底板共同变形最大挠度ω时，设其均在弹性变形范围内，且钢管梁以均布荷载的形式为底板提供横向支护反力。此时：底板的受力为巷道两帮的水平挤压力和钢管梁为抵抗变形而施加的垂直向下的支护反力，其中水平挤压力为底板弯曲的原因，变形挠度为δ，支护反力提供横向弯曲阻力，阻力挠度为−q；钢管梁受力为巷道两帮的水平挤压力，和接触面上底板垂直向上的横向力，其中水平挤压力不是梁产生弯曲变形的原因，而是在梁帮接触面上为梁提供约束力，限制梁两端的纵向位移，底板的挠曲变形的“趋势力”才是梁产生弯曲变形ω的主因。根据叠加原理：

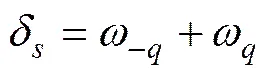
(18)

(19)

式中：If为底板的弯曲刚度。

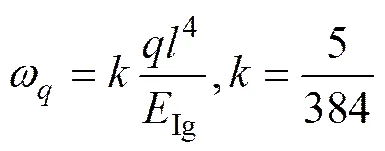
式中：Ig为钢管梁的弯曲刚度。

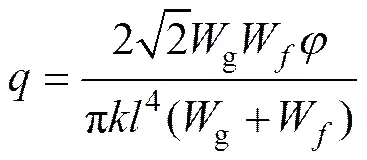
根据作用在钢管梁上的横向荷载，进行材料安全度验算，最大剪力，出现在巷道底板与支护的两端；最大弯矩，出现在巷道底板与支护的中部；在最大弯矩处存在最大应力(其中，z为弯曲截面系数)，之后可进行反算得出钢管梁的截面参数关系，用于支护设计参考。此外，=，取值为钢管梁外径1的1.5~2.0倍，排距，(其中，1和2分别为底板和钢管梁的泊松比，为安全系数)。

4 工程应用

试验巷道位于958分段，处在高构造应力场中，侧压系数约为2，返修之前出现了严重的底鼓现象。为了减弱巷道两帮收敛趋势，增大和提高底板抗压强度和抗弯刚度，结合钢管梁的几何和力学特性，设计多梁联合横撑底板两帮的巷道底鼓高强控制方案，根据式(17)~(20)，进行支护方案的设计与力学验算，最终确定钢管梁方案的布置参数：外径=220 mm，壁厚=16 mm，垫板400 mm，排距=600 mm。如图10所示，在巷道底板每隔600 mm开挖反拱槽，槽长4 200 mm，槽宽450 mm。底板开槽后，在槽内横向置放钢管梁，梁两端与巷道两帮接触；为分析支护方案控制巷道底鼓的效果，考虑中部与两端为应变主要发生区，如图11所示在钢管梁的中部和近端部布置应变片进行形变监测；最后向反拱槽内回填沙土，夯实整平，完成多梁联合横撑底板两帮支护方案的实施。根据监测数据显示，支护后30 d平均底鼓量减为原来的1/5，支护效果见图12。

(a) 下放钢管梁；(b) 钢管梁端部；(c) 水平排列钢管梁；(d) 回填砂土

图11 布置应变片

图12 支护效果

5 结论

1) 创建高侧压系数下的深埋巷道开挖计算模型，对巷道底鼓进行有限差分过程模拟。当巷道位于矿山深部高侧压系数的应力场中，其受到的水平应力大于垂直应力，底脚部位发生应力集中，导致底板两侧受到较大的水平应力的挤压作用，使底板产生弯曲变形趋势，当水平应力增大到一定程度，底板开始向裸露面发生形变，从而产生底鼓。随着侧压系数的增加，底鼓现象加重，且在0.5＜＜1.5时尤其明显，当＞2.0时，变化速率减缓，但仍呈增加趋势。

2) 构建底板受轴向力挠曲变形的力学分析模型，根据叠加原理，通过材料受轴向力挠曲变形计算模型与材料受均布荷载挠曲变形计算模型的转换，完成了巷道底板和支护材料共同作用的力学计算和机理分析。横撑巷道底板两帮的支护方式，能依靠材料自身的轴向承载能力，撑住巷道两帮，减弱两帮向内收敛挤压底板的趋势；横撑支护与底板直接接触，将底板的变形“裸露面”转换成抗弯刚度较高的支护载体即材料本身，从而为抵抗底板弯曲变形提供足够的横向支护反力；沿巷道走向布置钢管梁，构成多梁联合控制体系，使单梁的控制范围实现区域重叠，增强底板整体抗弯曲变形的能力。

3) 为减弱两帮收敛趋势和增强底板抗弯刚度，根据试验巷道围岩与应力情况，结合环形截面钢管梁几何和力学特性，设计多梁联合横撑底板两帮控制底鼓的支护方案，并完成了方案的计算与验证。经力学分析和现场试验发现，方案取得了良好的支护效果，能满足控制底板变形的要求，为矿山底鼓治理提供了新思路。

[1] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803−2813.HE Manchao, XIE Heping, PENG Suping, et al. Study on mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803−2813.

[2] 姜耀东, 赵毅鑫, 刘文岗, 等. 深部开采中巷道底鼓问题的研究[J]. 岩石力学与工程学报, 2004, 23(14): 2396−2401.JIANG Yaodong, ZHAO Yinxin, LIU Wengang, et al. Research on floor heave of roadway in deep mining[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(14): 2396−2401.

[3] CHANG Qingliang, ZHOU Huaqiang, XIE Zhihong et al. Anchoring mechanism and application of hydraulic expansion bolts used in soft rock roadway floor heave control[J]. International Journal of Mining Science and Technology, 2013, 23(3): 323−328.

[4] 孙玉宁, 周鸿超, 周建荣, 等. 煤岩软底巷道底鼓控制技术[J]. 采矿与安全工程学报, 2007, 24(3): 340−344. SUN Yuning, ZHOU Hongchao, ZHOU Jianrong, et al.Control technique of floor heave in semi coal and rock roadway with weak floor[J]. Journal of Mining & Safety Engineering, 2007, 24(3): 340−344.

[5] 康红普, 陆士良. 巷道底鼓机理的分析[J]. 岩石力学与工程学报,1991, 10(4): 362−373. KANG Hongpu, LU Shiliang.An analysis on the mechanism of roadway floor heave[J]. Chinese Journal of Rock Mechanics andEngineering, 1991, 10(4): 362−373.

[6] 曹平, 陈冲, 张科, 等. 金川矿山深部巷道围岩松动圈厚度测试与分析[J]. 中南大学学报(自然科学版), 2014, 45(8): 2840−2847.CAO Ping, CHEN Chong, ZHANG Ke, et al. Measurement and analysis of deep roadway surrounding rock loose zone in Jinchuan mine[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2840−2847.

[7] 孙利辉, 纪洪广, 杨本生, 等. 大采深巷道底板软弱夹层对底鼓影响数值分析[J]. 采矿与安全工程学报, 2014, 31(5): 695−701. SUN Lihui, JI Hongguang, YANG Bensheng, et al. Simulation analysis of influence of floor weak interlayer on floor heave in deep mining roadway[J]. Journal of Mining & Safety Engineering, 2014, 31(5): 695−701.

[8] 刘泉声, 刘学伟, 黄兴, 等. 深井软岩破碎巷道底臌原因及处置技术研究[J].煤炭学报, 2013, 38(4): 566−571. LIU Quansheng, LIU Xuewei, HUANG Xing, et al. Research on the floor heave reasons and supporting measures of deep soft-fractured rock roadway[J].Journal of China Coal Society, 2013, 38(4): 566−571.

[9] 周科平, 朱和玲, 肖雄, 等. 采矿环境再造连续开采地压演化过程的控制与仿真[J]. 中南大学学报(自然科学版), 2008, 39(3): 417−422.ZHOU Keping, ZHU Heling, XIAO Xiong, et al. Control And simulation of ground pressure evolutional process based on reconstructed mining environment and continuous caving method[J]. Journal of Central South University (Science and Technology), 2008, 39(3): 417−422.

[10] KANG Yongshui, LIU Quansheng, GONG Guangqing, et al. Application of a combined support system to the weak floor reinforcement in deep underground coal mine[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 71:13−150.

[11] 李学华, 王卫军, 侯朝炯, 等. 加固顶板控制巷道底鼓的数值分析[J]. 中国矿业大学学报, 2003, 32(4): 436−439.LI Xuehua, WANG Weijun, HOU Chaojiong, et al. Controlling floor heave with strengthening roof in gateway by numerical analysis[J]. Journal of China University of Mining & Technology, 2003, 32(4): 436−439.

[12] WANG Jiong, GUO Zhibiao, YAN Yunbiao, et al. Floor heave in the west wing track haulage roadway of the Tingnan Coal Mine mechanism and control[J]. International Journal of Mining Science and Technology, 2012, 22(3): 295−299.

[13] 杨本生, 贾永丰, 孙利辉, 等. 高水平应力巷道连续双壳治理底臌实验研究[J]. 煤炭学报, 2014, 39(8): 1504−1510.YANG Bensheng, JIA Yongfeng, SUN Lihui, et al. Experimental research on the continuous “double shell” harnessing floor heave in high horizontal stress roadway[J]. Journal of China Coal Society, 2014, 39(8): 1504−1510.

[14] 柏建彪, 李文峰, 王襄禹, 等. 采动巷道底鼓机理与控制技术[J]. 采矿与安全工程学报, 2011, 28(1): 1−5.BAI Jianbiao, LI Wenfeng, WANG Xiagyu, et al. Mechanism of Floor Heave and Control Technology of Roadway Induced by Mining[J]. Journal of Mining & Safety Engineering，2011, 28(1): 1−5.

[15] 刘泉声, 肖虎, 卢兴利, 等. 高地应力破碎软岩巷道底臌特性及综合控制对策研究[J]. 岩土力学, 2012, 33(6): 1703−1710. LIU Quansheng, XIAO Hu, LU Xiaoli, et al. Research on floor heave characteristics of broken soft rocks with high geo stress and its comprehensive control measures[J]. Rock and Soil Mechanics, 2012, 33(6): 1703−1710.

[16] 吴连元. 板壳理论[M]. 上海: 上海交通大学出版社, 1989: 472−515. WU Lianyuan. Theory of plates and shells[M]. Shanghai: Shanghai Jiaotong University Press, 1989: 472−515.

[17] 安龙, 徐帅, 任少峰, 等. 深部厚大矿体回采顺序设计及优化研究[J]. 东北大学学报(自然科学版), 2013, 34(11): 1642−1646.AN Long, XU Shuai, REN Shaofeng, et al. Study on design and optimization of mining sequence for deep and large ore body[J]. Journal of Northeastern University(Natural Science), 2013, 34(11): 1642−1646.

[18] 李中奎, 戴荣, 姜逸明. FLAC3D分析中的初始应力场生成及大型地下硐室群计算中的应用[J]. 岩石力学与工程学报, 2002, 21(2): 2387−2392.LI Zhongkui, DAI Rong, JIANG Yiming.Improvement of the generation of the initial stress field by using FLAC3Dand application in a huge undergroud cavern group[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(2): 2387−2392.

[19] SUN Xiaoming, WANG Dong, FENG Jili, et al. Deformation control of asymmetric floor heave in a deep rock roadway[J]. International Journal of Mining Science and Technology, 2014, 24(6): 799−804.

(编辑 陈爱华)

Mechanism and control of floor heave of deep buried roadway with high lateral pressure coefficient

CAO Ping, LI Haoyue, ZHONG Yongfang, WANG Fei

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Based on the theoretical analysis, numerical simulation, mechanical calculation and field investigation, the numerical simulation of the floor heave of the roadway with different lateral pressure coefficients was completed, the deformation law of the roadway with a high lateral pressure coefficient was discussed, the analysis of the floor-transverse supporting’s interaction mechanism was finished, the calculation of the model conversion was completed and the scheme of the controlling the floor heave with transverse supporting was verified. The results show that: with a high lateral pressure coefficient, the high horizontal stress near the sides of floor extrudes the floor to display flexure deformation toward the free-surface of the floor, and the process of the floor heave is divided into four stages: accelerated deformation, uniform-speed deformation, slowdown deformation and ultimate stability. As the lateral pressure coefficient increases, the phenomena of the floor heave become more serious. When 0.5＜＜1.5, the phenomena are serious obviously; while＞2.0, the speed of the variation slows down, but the phenomena still increases. Because of the effect of transverse bracing the sides of the floor, the supporting reduces the tendency of high horizontal stress near the floor’s sides extruding the floor from sides to central, and the supporting can provide enough supporting force to resist the deformation of the floor. Forming on the layout of steel beams along with roadway, the combination-control system of multi-beams overlaps the control range of single beam, resulting in raising the bending strength of the whole floor.

mining engineering; lateral pressure coefficient; floor heave of roadway; control of floor heave

10.11817/j.issn.1672−7207.2017.02.025

TD32

A

1672−7207(2017)02−0457−08

2016−03−25；

2016−06−20

国家自然科学基金资助项目(51274249)；教育部博士点基金资助项目(20120162110009)(Project(51274249) supported by the National Natural Science Foundation of China; Project(20120162110009) supported by Specialized Research Fund for the Doctoral Program of Higher Education)

曹平，教授，博士生导师，从事岩石力学研究；E-mail：pcao_csu@sina.com