基于响应面法的三维H−B强度准则可靠度的研究

朱唤珍，李夕兵，宫凤强



基于响应面法的三维H−B强度准则可靠度的研究

朱唤珍，李夕兵，宫凤强

(中南大学，资源与安全工程学院，湖南长沙，410083)

针对采用一次二阶矩法计算复杂、高度非线性功能函数的可靠指标时，求解功能函数对随机变量的偏导数极其困难，并且偏导数形式非常复杂等问题，提出用响应面函数代替原功能函数的方法，使其求导过程方便，并且使偏导数形式转化为随机变量的线性表达式，便于程序化求解。然后以计算三维Hoek−Brown强度准则的可靠度为例，确认响应面法在复杂、高度非线性功能函数可靠度计算中的可行性，并与变量代换法和复合函数求导法则的计算结果进行比较，说明利用响应面法计算的结果具有较高的精度。最后，用响应面法分析强度准则参数分布类型和岩体参数之间的相关性对三维Hoek-Brown准则可靠度的影响规律。研究结果表明：该方法具有较高精度；强度准则参数分布类型对可靠指标的敏感性较弱；岩体参数的负相关系数与可靠指标线性相关，对可靠指标的影响不大。

Hoek−Brown准则；响应面法；高度非线性的功能函数；偏导数

在结构可靠度分析和计算中，比较常用的有中心点法、验算点法、JC法和考虑随机变量相关性的广义随机空间内的可靠度分析方法。这些可靠度计算方法大都是建立在功能函数为简单、弱非线性解析表达式的基础上[1]，但对于某些复杂结构系统如三维Hoek−Brown经验强度准则(简称为H−B准则)表示的极限状态，其功能函数往往具有高度非线性或非常复杂的特征。目前功能函数对随机变量偏导数的求解方法主要有变量代换法、复合函数链式求导法、有限差分法和有理多项式技术等[2]，但这些方法都是基于原功能函数直接求解，求解过程复杂，尤其是变量代换法和复合函数链式求导法则很难能给出偏导数具体的表达形式。为此，本文提出利用响应面法解决上述问题。国内很多学者基于响应面法分析了边坡的可靠 度[3−6]。LI等[3−4]提出了边坡可靠度分析的随机响应面法，分析了具有相关非正态分布变量的边坡可靠度问题。傅方煜等[5]基于响应面法和SORM理论(二阶可靠度方法)，提出了边坡可靠度分析的实用算法，即在U空间内构造响应面函数，在空间内计算试验点的函数值，在生成响应面函数的基础上，进行一阶或二阶可靠度分析。彭振斌等[6]将传统响应面分析方法与Bishop条分法相结合，提出了一种新的边坡稳定可靠性响应面分析方法。近年来，响应面法由于原理简单、方便易行、适用性强，在可靠度领域引起了众多学者的兴趣[7−8]。赵威等[9−10]将偏最小二乘法应用于响应面法的可靠度分析中，有效地解决了变量间多重相关性及小样本条件下建立回归模型的问题。赵维涛等[11]基于切平面布点对响应面法进行了改进。但以上研究方法主要针对隐式功能函数或功能函数不能明确表达的岩土工程或结构的可靠度问题。尽管LÜ等[12−13]将响应面法用于求解用显示功能函数表达的地下圆形隧道的可靠度分析，然而，将响应面法用于求解如三维H−B强度准则表达的复杂、高度非线性功能函数的可靠指标研究较少。为此，本文作者用响应面法拟合的响应面函数代替原复杂的功能函数，从而简化功能函数对随机变量偏导数的求解过程，然后利用广义随机空间内的JC法计算包含非正态相关随机变量功能函数的可靠指标，并用三维H−B强度准则表达的功能函数验证响应面法计算复杂、高度非线性功能函数可靠度问题的可行性。在此基础上，利用该方法分析强度准则参数的分布类型和岩体参数的相关性对三维H−B强度准则可靠度的影响。

1 响应面法

响应面法是一种统计学的综合实验技术，专门用于处理复杂系统的输入(基本变量)和输出(系统响应)的转换关系问题[14]。该方法通过采用有限试验回归拟合得到解析表达式即响应面函数，再用常规可靠度分析方法求解高度非线性功能函数的可靠指标和验算点。利用上述方法计算可靠度的原理如下。

设含有个随机变量1，2，…，X的极限状态方程为

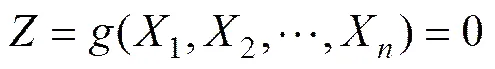
响应面函数的形式应当尽可能简单，并使待定系数尽量减少，以减小复杂结构可靠度分析的工作量。目前常用的响应面函数的形式为二次多项式，更高次的响应面函数由于概念上和计算上的原因，通常不予采用；线性响应面函数形式最简单，待定系数也最少，但在拟合非线性程度较高的功能函数时精度不高。不含交叉项的二次多项式可以在验算点附近很好地拟合复杂功能函数[15−17]，这保证了用响应面函数求解可靠度计算中最为关心的可靠指标和验算点的精度。本文选用响应面函数的形式为

(2)

式中：，b和c为表达式的待定参数，为响应面函数。从式(2)可知，确定响应面函数的关键是确定，b和c，共2+1个系数。本文采用中心复合设计方法，得到2+1个试验点，即和，将响应面函数待定系数的求解转化为求解2+1个线性方程组解的问题，即

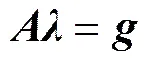
其中：

；

。

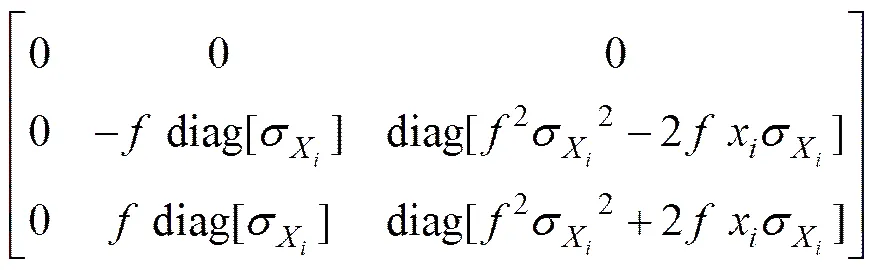
显然，在每一次迭代过程中，要求响应面函数是唯一的，这就要求上述线性方程组的解是唯一的，为此，系数矩阵必须是非奇异矩阵。下面给出具体的证明过程。

||经过等价变换可以化为如下形式：

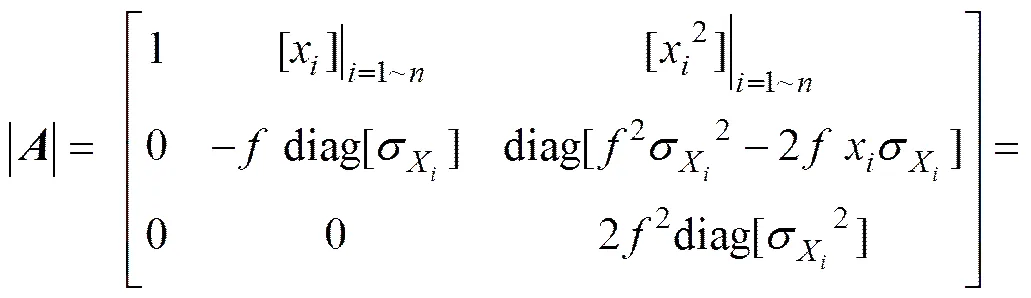
这就证明了系数矩阵是可逆矩阵，由2+1个试验点得到的2+1个线性方程构建的线性方程组有唯一解，拟合得到的响应面函数是唯一的。因此，本文采用矩阵求逆的方法计算响应面函数的待定系数，即

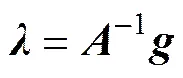
响应面函数对随机变量的偏导数为

(5)

用响应面函数代替原功能函数后，再根据广义随机空间内JC法计算可靠指标和验算点。

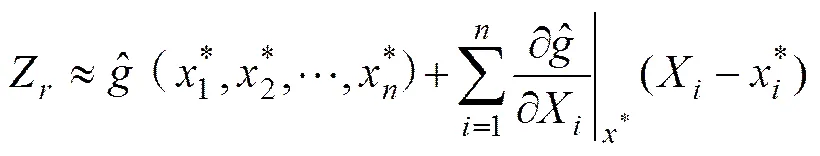
因此，Z的均值、均方差分别为

(7)

灵敏度系数为

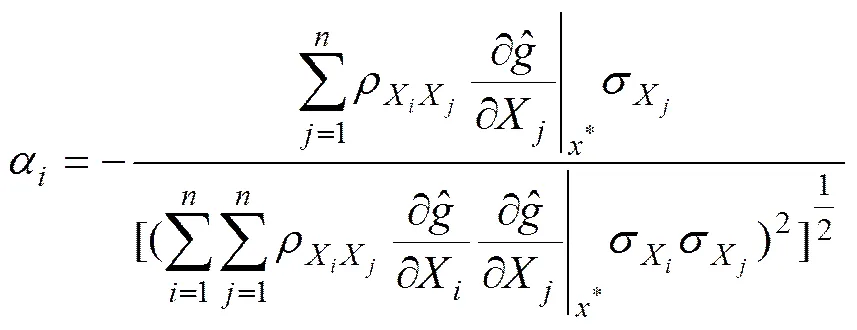
可靠指标为

(9)

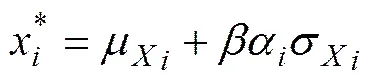
由于非正态分布随机变量的当量正态化并不改变随机变量的线性相关性，即在当量正态化过程中保持不变，所以，对于非正态随机变量可以通过当量正态化转化为等效的正态随机变量，然后，将等效正态随机变量的均值和均方差代入式(7)~(10)进行计算。下面以三维H−B经验强度准则的可靠指标计算为例，研究响应面法在求解复杂、高度非线性的显示功能函数中的应用。

2 三维H−B强度准则可靠度计算 方法

长期以来，人们对岩体在外力作用下的破坏准则进行了大量研究，其中H−B强度准则是目前最有影响应用也最广泛的强度准则之一[18]。但是经典的H−B强度准则未考虑中间主应力的影响，相关研究者对此进行了深入研究，并先后提出了考虑中间主应力影响的多种三维H−B强度准则[19−20]。实际上，由于岩土自身具有错综复杂的变异性质，且岩体本身存在内部微裂隙，使得岩体强度参数表现出极大的随机性和离散性。忽略岩体强度准则参数的随机性和离散性，会给计算结果带来较大的误差[21−22]，因此，对以H−B经验强度准则表达的功能函数进行可靠度研究显得极其重要，用响应面法计算该准则可靠度的具体步骤 如下。

采用三维H−B强度准则表达的极限状态方 程[23]为

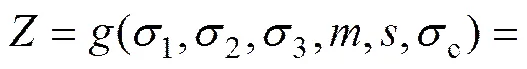
(11)

由式(11)可见，该极限状态方程是高度非线性的，而且非常复杂，用常规计算可靠指标的方法不易求解，而且会带来较大误差。

令X(=1~6)分别为s和，采用表征三维H−B强度准则极限状态方程的响应面函数的形式为不含交叉项的二次多项式，即

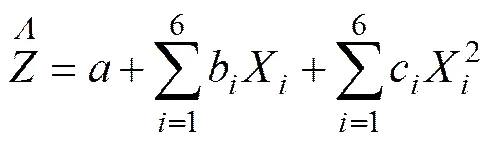
式(12)使由式(11)表达的高度非线性和复杂的功能函数变得极其简单，功能函数对随机变量偏导数的求解也十分方便，而且求解过程便于程序化进行。

利用响应面函数代替式(11)表示的功能函数，结合广义随机空间内的JC法计算可靠指标及其验算点，其中功能函数对随机变量的偏导数用式(5)代替。求解三维H−B强度准则的验算点和可靠指标的具体步骤如下。

3) 将式(12)得到的13个样本点代入式(3)，可得含有13个待定系数的线性方程组的表达式为

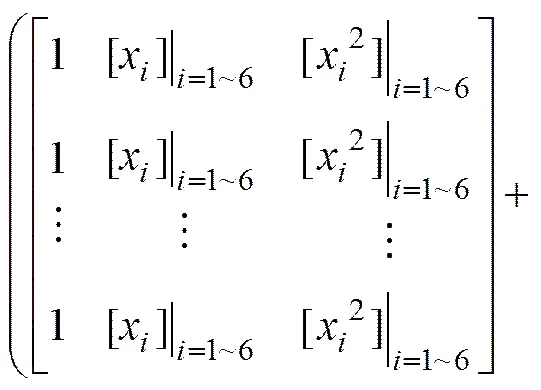
根据式(4)可计算得到响应面函数的13个待定系数，然后将之回带到式(12)即可得到响应面函数的具体表达式。

4) 用广义随空间内的JC法计算可靠指标及其相应的验算点*，其中功能函数对随机变量的偏导数利用式(5)计算。

5) 计算*处的原功能函数值。

6) 利用下式插值计算新的：

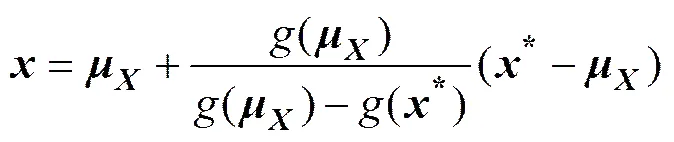
7) 重复步骤2)~6)，直至前、后两次||||相差小于为止(文中取=10−6)。

3 算例分析

对文献[24−25]中三维H−B准则可靠度算例进行具体计算，已知某岩体参数均值和方差见表1，求解岩体可靠指标。

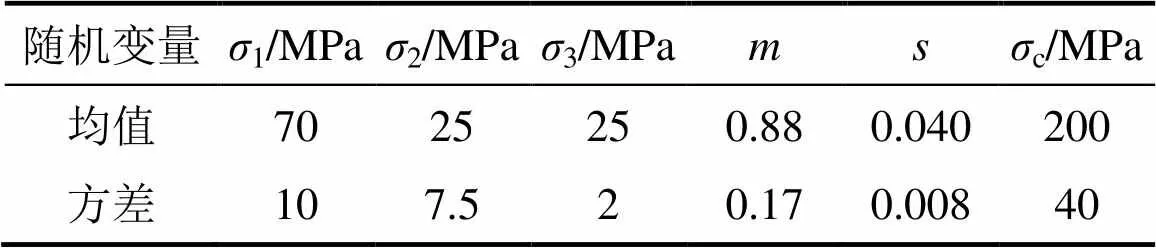
表1 强度准则参数及其统计特征

3.1 计算结果分析与比较

计算结果见表2，表2同时列出了文献[24]和[25]分别利用变量代换法和复合函数链式求导法则所得计算结果。在岩土工程的可靠度分析中，其可靠指标都可以通过Monte Carlo模拟计算得到。理论上，试验次数越多，得到的计算结果越精确。试验次数取决于期望的失效概率及其变异系数，对于通常的实际工程结构而言，f为10−3~10−5量级，若相对误差小于20%的置信度为95%，则所需要的模拟次数=95 940~ 9 603 551即可[1]。为了保证计算结果的精确性，针对上述3种方法，以Monte Carlo模拟100万次的计算结果作为基本参考值进行比较。

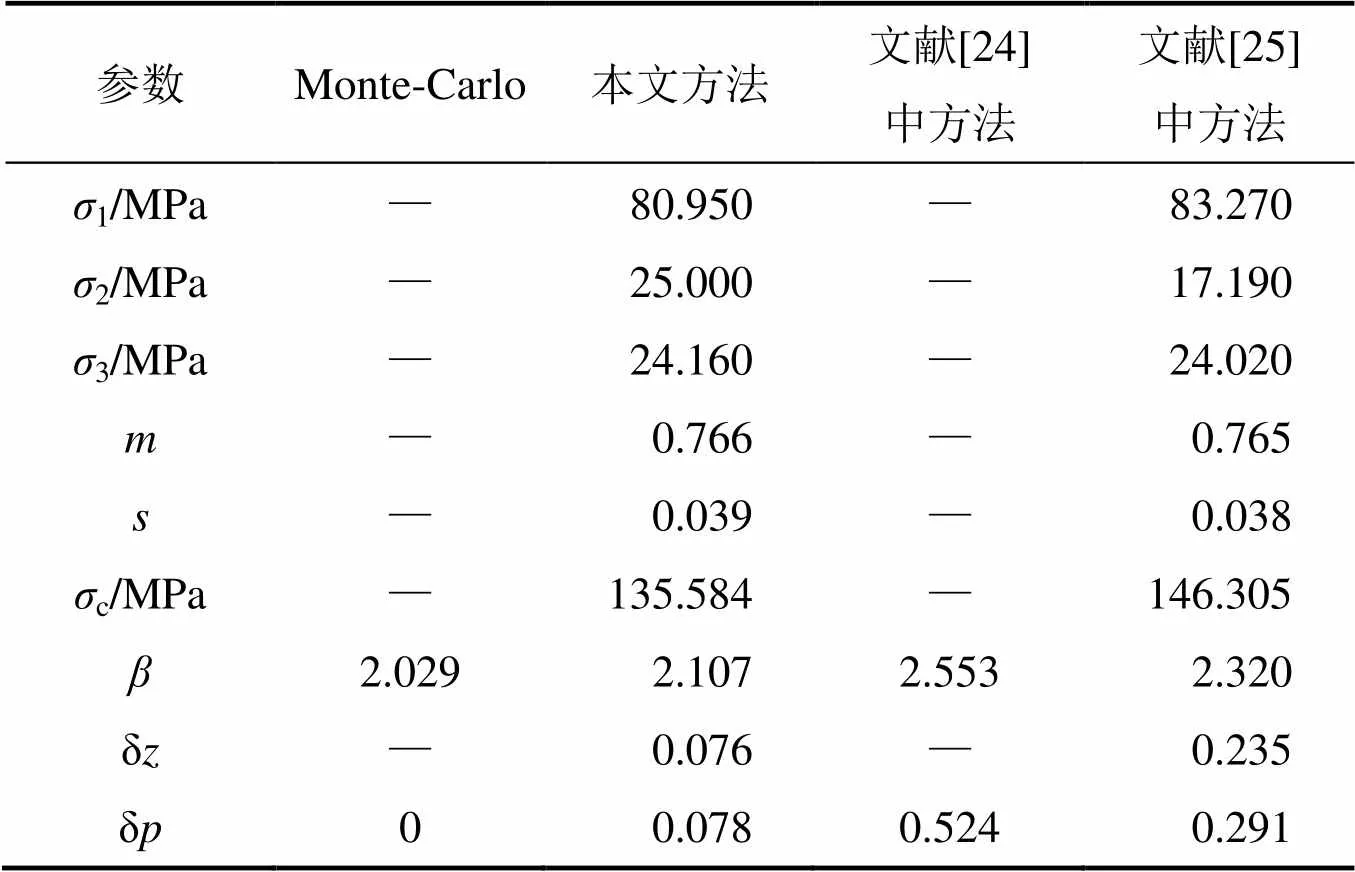
表2 本文计算结果与文献[24−25]中计算结果的比较

注：1) δ为将计算得到的验算点代入式(11)得到的误差； 2) δ为可靠指标的误差。

从表2可以看出：响应面法所得计算结果为2.107，与Monte Carlo模拟方法计算的结果2.029相比仅相差0.078，而且将验算点带入原功能函数的误差也只有0.076；文献[24]采用变量代换法计算的可靠指标误差最大，为0.524，且不能给出可靠度计算中验算点的值；文献[25]利用复合函数求导法则，也能够计算得到验算点，并且计算得到的可靠指标为2.320，其精度较文献[24]中方法所得结果提高了80.07%，误差却是本文方法所得结果的2.73倍。

比较分析上述计算结果，可知本文方法求解非线性功能函数可靠度的可行性，并且具有较高的精度。下面用本文方法分析准则参数的分布类型和岩体参数的相关性对三维H−B强度准则可靠指标的影响规律。

3.2 参数分布类型对可靠指标的敏感性分析

在三维H−B强度准则的可靠度计算中，岩体参数和以及单轴抗压强度的分布类型可通过大量试验结果进行统计分析得到；主应力，和可以通过随机有限元或室内试验得到。经大量试验统计分析单轴抗压强度一般为非正态分布随机变量[24−25]。本文用响应面法探讨H−B经验强度准则参数的分布类型对可靠指标的影响规律，并分析当主应力，和以及岩体参数和都为相互独立的正态随机变量时，单轴抗压强度的分布类型(分别为正态分布、对数正态分布和极值1型分布)对三维H−B强度准则可靠指标的敏感性，计算结果见表3。

从表3可以看出：强度准则参数的不同分布类型对可靠度有一定影响；当所有强度准则参数都服从极值1型分布时，可靠指标最小，为1.957，可靠指标误差为0.071；强度准则参数都服从正态分布时，可靠指标为2.106，误差为0.077；均服从对数正态分布时，误差为0.017，可靠指标介于二者之间。

表3 强度准则参数的分布类型对可靠指标的影响

通过上述分析可知，本文方法计算得到的可靠指标与Monte Carlo计算得到的可靠指标非常接近，再次证明了用本文方法计算高度非线性功能函数可靠指标的可行性。

3.3 参数相关性对可靠指标的影响

岩体参数和是1对具有负相关性的随机变量，忽略岩体参数的相关性可能会给计算结果带来影 响[24]。因此，本文分析强度准则参数服从不同概率分布时，岩体参数和的相关性对可靠指标的影响，计算结果见表4和图1。

分析表4和图1可知：H−B经验强度准则参数的分布类型和岩体参数之间的相关性对可靠指标有一定的影响；当和的相关性为某一定值时，强度准则的可靠指标与和为相互独立随机变量的情况一致，即当服从极值1型分布，其他参数均服从正态分布时，可靠指标最大；当所有参数均服从极值1型分布时，可靠指标最小；当和的相关性从相互独立逐渐变化到完全负相关时，可靠指标均逐渐增大，但增加幅值与参数的分布类型有关；当为极值1型分布，其他均为正态分布时，可靠指标从2.139逐渐增大到2.271，增加幅值最大，为0.132；当所有参数均服从极值1型分布时，可靠指标从1.956增大到2.014，增加幅值最小，为0.058；当参数服从其他分布时，增加幅值介于二者之间。从图1还可以看出：参数服从上述分布类型时，可靠指标与负相关系数近似线性相关；当参数均服从极值1型分布时，斜率最小；参数服从其他4种分布时，斜率大致相等。

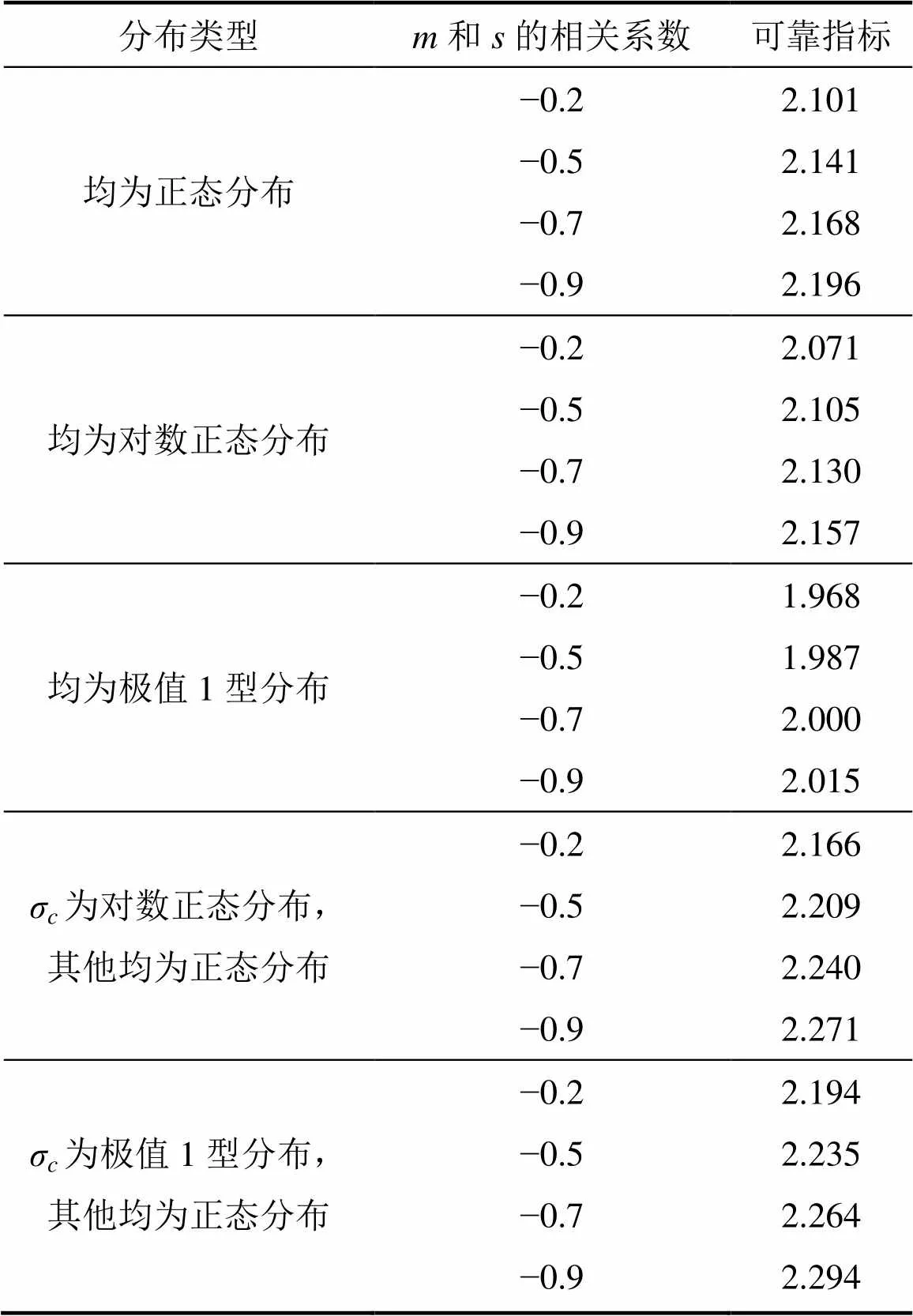
表4 强度准则参数相关性对可靠指标的影响

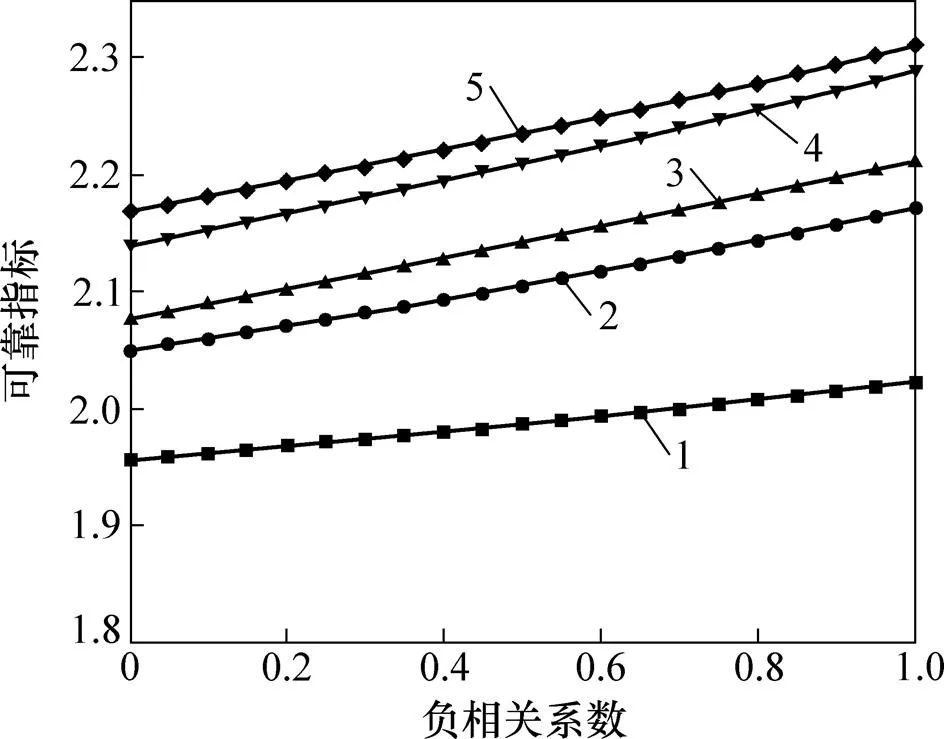
1—均为正态分布；2—均为对数正态分布；3—均为极值1型分布；4—单轴抗压强度为对数正态分布；5—单轴扰压强度为极值1型分布。

4 结论

1) 用响应面法的迭代格式得到在验算点能近似代替复杂的、高度非线性的功能函数的响应面函数。该函数形式简单，对随机变量的偏导数的求解也非常容易，便于程序化，在精度上也能满足实际工程和理论研究的需求，是一种求解复杂、高度非线性功能函数可靠度问题的行之有效的方法。

2) 本文方法不仅能计算出的可靠指标和验算点，而且能够得到较高的计算精度，说明将响应面法用于求解高度非线性功能函数可靠指标和验算点的可 行性。

3) 用响应面法分析准则参数的分布类型以及岩体参数和的相关性对强度准则可靠度的影响，得出准则参数的分布类型对可靠指标的敏感性较弱，和的相关性对可靠指标的影响也较小。

[1] 张明. 结构可靠度分析—方法与程序[M]. 北京: 科学出版社, 2009: 19−32. ZHANG Ming. Structural reliability analysis-methods and procedures[M]. Beijing: Science Press, 2009: 19−32.

[2] 谭晓慧, 王建国, 刘新荣.改进的响应面法及其在可靠度分析中的应用[J]. 岩石力学与工程学报, 2005, 24(S2): 5874−5879. TAN Xiaohui, WANG Jianguo, LIU Xinrong. Improved response surface method and its application to reliability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S2): 5874−5879.

[3] LI D Q, CHEN Y F, LU W B, et al. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables[J]. Computers and Geotechnics, 2011, 38(1): 58−68.

[4] 李典庆, 周创兵, 陈益峰, 等. 边坡可靠度分析的随机响应面法及程序实现[J]. 岩石力学与工程学报, 2010, 29(8): 1513−1523. LI Dianqing, ZHOU Chuangbing, CHEN Yifeng, et al. Reliability analysis of slope using stochastic response surface method and code implementation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1513−1523.

[5] 傅方煜, 郑小瑶, 吕庆, 等. 基于响应面法的边坡稳定二阶可靠度分析[J]. 岩土力学, 2014, 35(12): 3460−3466. FU Fangyu, ZHENG Xiaoyao, LÜ Qing, et al. Second order reliability analysis of slope stability using response surface method[J]. Rock and Soil Mechanics, 2014, 35(12): 3460−3466.

[6] 彭振斌, 李俊, 彭文祥. 基于 Bishop 条分法的边坡可靠度应用研究[J]. 中南大学学报(自然科学版), 2010, 41(2): 668−672.PENG Zhenbin, LI Jun, PENG Wenxiang. Application analysis of slope reliability based on Bishop analytical method[J]. Journal of Central South University (Science and Technology), 2010, 41(2): 668−672.

[7] LIU Ji, LI Yun. An improved adaptive response surface method for structural reliability analysis[J]. Journal of Central South University, 2012, 19: 1148−1154.

[8] CHEN Jianyun, XU Qiang, LI Jing, et al. Improved response surface method for anti-slide reliability analysis of gravity dam based on weighted regression[J]. Journal of Zhejiang University SCIENCE A, 2010, 11(6): 432−439.

[9] 赵威, 王伟. 偏最小二乘回归在响应面法可靠度分析中的应用[J]. 工程力学, 2013, 30(2): 272−277.ZHAO Wei, WANG Wei. Application of partial least squares regression in response surface for analysis of structural reliability[J]. Engineering Mechanics, 2013, 30(2): 272−277.

[10] 赵威, 王伟. 非线性偏最小二乘回归法在均匀设计响应面法中的应用[J]. 航空学报, 2012, 33(5): 839−847.ZHAO Wei, WANG Wei. Application on non-linear partial least squares regression method to response surface method with uniform design[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(5): 839−847.

[11] 赵维涛, 邱志平. 基于切平面布点的一种改进响应面方法[J]. 工程力学, 2014, 31(10): 21−26. ZHAO Weitao, QIU Zhiping. An adaptive response surface method based on the selection of experimental points using tangent plane[J]. Engineering Mechanics, 2014, 31(10): 21−26.

[12] LÜ Q, LOW B K. Probabilistic analysis of underground rock excavations using response surface method and SORM[J]. Computers and Geotechnics, 2011, 38(8): 1008−1021.

[13] LÜ Q, SUN H Y, LOW B K. Reliability analysis of ground–support interaction in circular tunnels using the response surface method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1329−1343.

[14] 黄靓, 易伟建, 汪优. 岩土工程可靠度分析的改进响应面法研究[J]. 岩土力学, 2008, 29(2): 370−374. HUANG Liang, YI Weijian, WANG You. Improvement study on response surface method for reliability analysis in geotechnical engineering[J]. Rock and Soil Mechanics, 2008, 29(2): 370−374.

[15] 张哲, 李生勇, 石磊, 等. 结构可靠度分析中的改进响应面法及其应用[J]. 工程力学, 2007, 24(8): 111−115. ZHANG Zhe, LI Shengyong, SHI Lei, et al. An improved response surface method for structural reliability analysis and its application[J]. Engineering Mechanics, 2007, 24(8): 111−115.

[16] 王宇, 王春磊, 汪灿, 等. 边坡可靠性评价的向量投影响应面研究及应用[J]. 岩土工程学报, 2011, 33(9): 1434−1439. WANG Yu, WANG Chunlei, WANG Can, et al. Reliability evaluation of slopes based on vector projection response surface and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 33(9): 1434−1439.

[17] 何军涛, 张洁, 黄宏伟, 等. 基于多重响应面法的基坑位移反分析[J]. 岩土力学, 2012, 33(12): 3810−3817. HE Juntao, ZHANG Jie, HUANG Hongwei, et al. Back analysis of displacements of excavation based on multiple response surface method[J]. Rock and Soil Mechanics, 2012, 33(12): 3810−3817.

[18] 宫凤强, 侯尚骞, 岩小明. 基于正态信息扩散原理的 Mohr-Coulomb 强度准则参数概率模型推断方法[J]. 岩石力学与工程学报, 2013, 32(11): 2225−2234. GONG Fengqiang, HOU Shangqian, YAN Xiaoming. Probability model deduction method of Mohr-Coulomb criteria parameters based on normal information diffusion principle[J]. Chinese Journal of Geotechnical Engineering, 2013, 32(11): 2225−2234.

[19] 昝月稳, 俞茂宏, 王思敬. 岩石的非线性统一强度准则[J]. 岩石力学与工程学报, 2002, 21(10): 1435−1441. ZAN Yuewen, YU Maohong, WANG Sijing. Nonlinear unified strength criterion of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(10): 1435−1441.

[20] 朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945−1963. ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progression and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945−1963.

[21] 姜彤, 马莎, 李永新. 抗剪强度，值概率分布对边坡可靠性分析的影响[J]. 华北水利水电学院学报, 2004, 25(3): 46−49.JIANG Tong，MA Sha，LI Yongxin. The study of effect on the reliability of rock slope by different probability distributionsof shear strength,[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2004, 25(3): 46−49.

[22] 严春风, 刘东燕, 张建辉, 等. 岩土工程可靠度关于强度参数分布函数概型的敏感性分析[J]. 岩石力学与工程学报, 1999, 18(1): 36−39. YAN Chunfeng, LIU Dongyan, ZHANG Jianhui, et al. The susceptibility analysis of reliability for the probability distribution types of parameters in strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(1): 36−39.

[23] 严春风, 徐健, 何翠香. 节理岩体Hoek-Brown经验强度准则可靠度分析[J]. 岩土工程学报, 1999, 21(5): 500−553. YAN Chunfeng, XU Jian, HE Cuixiang. The reliability analysis of the Hoek-Brown empirical strength criterion for rockmass[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(5): 550−553.

[24] 陈彦峰. 岩体强度准则可靠度研究和参数敏感度分析[D]. 重庆: 重庆建筑大学岩土工程研究所, 1998: 42. CHEN Yanfeng, Reliability research of rock strength criterion and sensitivity analysis of parameters[D]. Chongqing: Faculty of Civil Engineering, Chongqing Jianzhu University, 1998: 42.

[25] 徐军, 刘东升, 郑颖人.用改进的JC方法分析三维Hoek−Brown准则的可靠度[J]. 岩土力学, 1999, 20(1): 44−47. XU Jun, LIU Dongsheng, ZHENG Yingren. Reliability analysis of 3D Hoek−Brown criterion by the improved JC method[J]. Rock and Soil Mechanics, 1999, 20(1): 44−47.

(编辑 陈灿华)

Reliability analysis of 3d H−B strength criterion based on the response surface method

ZHU Huanzhen, LI Xibing, GONG Fengqiang

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Consideringthatit is very difficult for the FOSM to solve partial derivatives of performance function because random variables and the forms of partial derivatives are very complex in calculating the reliability index of complex, high order nonlinear performance function, the response surface method which used the response surface function to replace the original function was proposed. The solving process of function’s derivation was convenient and the form of the partial derivative was a linear expression of random variables. Based on the 3D Hoek Brown strength criterion for the limit state function, the response surface method was adopted to calculate the reliability index, which assured that this method was suitable for the complex and high-nonlinear performance function. Moreover, the variables replacing technique and the compound function method were employed as comparison. The results show that this method has higher accuracy, and the probability distribution of the basic random variables has less effect on the reliability index. The correlation of rock mass parameters and the relation between the reliability index and negative correlation coefficient of rock mass parameters is linear.

3D Hoek−Brown criterion; the response surface method; the high order nonlinear performance function; partial derivative

10.11817/j.issn.1672−7207.2017.02.029

TU 443

A

1672−7207(2017)02−0491−07

2016−02−22；

2016−04−24

国家重点基础研究发展计划(973计划)项目(2010CB732004)；国家自然科学基金资助项目(41272304, 11472311)(Project (2010CB732004) supported by the National Basic Research Development Program(973 Program) of China; Projects(41272304, 11472311) supported by the National Natural Science Foundation of China)

李夕兵，教授，博士生导师，从事岩石动力学与采矿工程研究； Email：xbli@csu.edu.cn