应用于离网型风力发电系统的无源MPPT方法

白崟儒，寇宝泉，陈清泉



应用于离网型风力发电系统的无源MPPT方法

白崟儒，寇宝泉，陈清泉

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨，150001)

针对离网型风力发电系统所使用的传统最大功率点跟踪(MPPT)方法可靠性相对较低，提出无源MPPT方法。采用此方法的新型发电机系统由1台双绕组永磁发电机、2个不可控整流器、1台蓄电池和负载构成。通过特殊设计系统结构，新型发电机系统的输入功率特性曲线与风力机的最大功率曲线相吻合，从而保证系统能够在不使用任何电控装置的情况下自动地实现MPPT，因此新型发电机系统具有较高的可靠性。通过分析无源MPPT的跟踪过程，阐明无源MPPT方法的原理。研究并建立新型发电机系统的数学模型。研究结果表明：当风速变化时，采用无源MPPT方法的新型发电机系统能够准确地实现MPPT，并且其动态性能优于使用爬山法传统系统的动态性能。

最大功率点跟踪(MPPT)；无源；永磁同步发电机；离网；风力发电

离网型风力发电系统(SWPGS)具有成本低、应用灵活、维护简便等优点，近年来被越来越多地应用于牧区、林区、通讯基站、气象站、海岛及边防哨所等场所[1−6]。SWPGS一般采用定浆距变速风力机。然而当风速变化时，变速风力机不能持续地运行在最大功率点(MPP)，需要进行最大功率点跟踪(MPPT)控制[7−9]。因此，MPPT技术是当前的研究热点。各国学者们提出了各种MPPT方法。这些方法大致可被分为3种类型：功率反馈(PSF)控制方法、爬山搜索(HCS)控制方法以及基于模糊逻辑和神经网络的控制方 法[9]。PSF控制方法是一种快速、高效的MPPT方法。该方法需要已知系统特性，这种特性可以是发电机系统的各种特性[10]，如输出功率与整流直流电压特性[11]或整流直流电压与整流直流电流特性[12]。这些系统特性通过实验获得，然后被存储在控制器的内存中，以便服从程序调用。学者们对PSF控制方法进行了大量研究，取得了许多研究成果。PAN等[13]提出了一种具有自适应能力的PSF控制方法，提高了系统的风能捕捉能力。CHEN等[14]提出了具有恒定带宽的PSF控制方法，有效地扩大了其在低风速时的追踪带宽。MORIMOTO等[15]提出了基于损耗最小的PSF控制方法，有效地减小了系统损耗。在此基础上，ZHU等[16]进一步地考虑了传动轴上的转矩损耗，提出了更高效的PSF控制方法。HCS控制方法也被称为观测扰动 法[17−18]，其不需要已知系统特性，因此可以方便地应用于各种参数的风力发电系统，是SWPGS最常用的MPPT控制方法。国内外学者们对HCS方法开展了大量研究，提出了各种HCS方法。WANG等[19]提出一种智能HCS方法，加快了系统的响应速度。AGARWAL等[20]提出了一种变步长的HCS方法，解决了搜索速度与MPPT效率的权衡问题。DALALA 等[21]提出了一种改进型HCS方法，解决了搜索方向容易出错的问题。除了上述常见的2类MPPT方法，还提出了基于模糊逻辑和神经网络的控制方法。SIMOES等[22]提出了一种具有三模糊逻辑级别的MPPT控制方法。GALDI等[23]提出了一种基于Takagi-Sugeno-Kang 模糊逻辑模型的MPPT控制方法。LI等[24]提出了基于神经网络的MPPT控制方法。张秀玲等[25]提出了基于模糊推理最优梯度法的MPPT方法。上述MPPT方法虽各不相同，却都有一个共同特征，即都需要使用电控装置，因此，它们可以被统一地归为同一种类型：电控MPPT方法。SWPGS通常用于野外，时常面对雨、雪、风沙等恶劣天气，因而电控装置中的电子器件非常容易损坏，进而导致整个系统故障。因此，数量众多的电子器件降低了系统的可靠性，不利于SWPGS在野外环境稳定地运行。针对此问题，本文作者提出无源MPPT方法。该方法基于对发电机系统结构进行特殊设计，使发电机系统的输入功率曲线与风力机的MPP曲线相吻合，从而无需电控装置和控制算法系统就能自动地实现MPPT。由于舍弃了电控装置，该方法具有较高的可靠性。

1 无源MPPT方法的原理

风力机输出的功率为

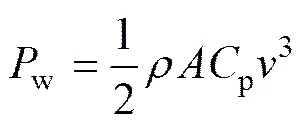
其中：w为风力机输出机械功率；p为风力机的功率系数，其值是桨距角和叶尖速比的函数；为风速；为空气密度；为风力机扫掠面积。

SWPGS通常采用定桨风力机，所以p只由叶尖速比决定。叶尖速比的计算公式为

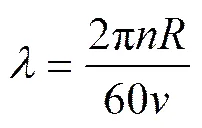
其中：为风力机叶片的半径；为叶尖速比；为 转速。

根据式(1)与式(2)，可以绘制出风力机在不同风速下的w与关系曲线。连接其在不同风速下功率的最大点可以获得风力机的MPP曲线，如图1所示。风力机MPP曲线数值的计算式为

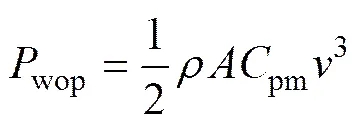
其中：wop为风力机的MPP数值；pm为风力机的最大功率系数。

式(3)表明：风力机的MPP数值正比于3。式(3)也可表示为

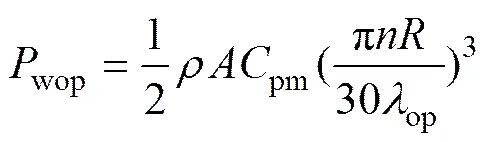
其中：op为最佳叶尖速比。

式(4)表明：当风力机保持最佳叶尖速比的时候，风力机的MPP数值正比于3。由能量守恒定律可知，SWPGS的动态能量方程为

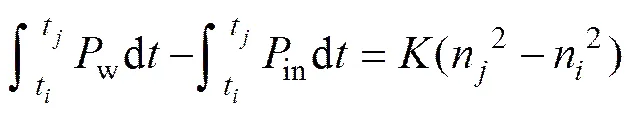
图1 风力机特性

Fig. 1 Wind turbine characteristics

式(5)表明：在任意一段时间内(时间长度为t−t)，如果风力机的输出能量大于(小于)发电机系统的输入能量，则系统的转速上升(下降)；若两者相等，则转速不变。图2所示为整个SWPGS的能量流程示意图，图中：loss为发电机系统的损耗；out为发电机系统的输出功率。图3所示为传统离网型风力发电系统。

由电机理论可知：发电机系统的输入功率in是转速的函数。图3(a)和图4所示为未采用任何MPPT方法的传统发电机系统的输入功率特性曲线(即in与关系曲线)。由图4可见：in曲线的斜率随着转速上升而逐渐减小，导致其偏离风力机的MPP曲线，因此传统离网型风力发电系统无法实现MPPT。为解决这一问题，各国学者们提出了电控MPPT方法：在系统中添加DC/DC变换器(图3(b))，然后通过控制系统电流，改变系统的输入功率特性曲线，使其与风力机的MPP曲线相吻合，从而实现MPPT。基于此，本文从相反的思维角度提出无源MPPT方法：如果对发电机系统的本体结构进行特殊设计，使发电机系统具有与风力机MPP曲线相吻合的输入特性(见图5)，则无需使用昂贵的电控装置和复杂的控制算法，系统就能够自动地实现MPPT。下文通过分析无源MPPT的跟踪过程，论证无源MPPT的机理。

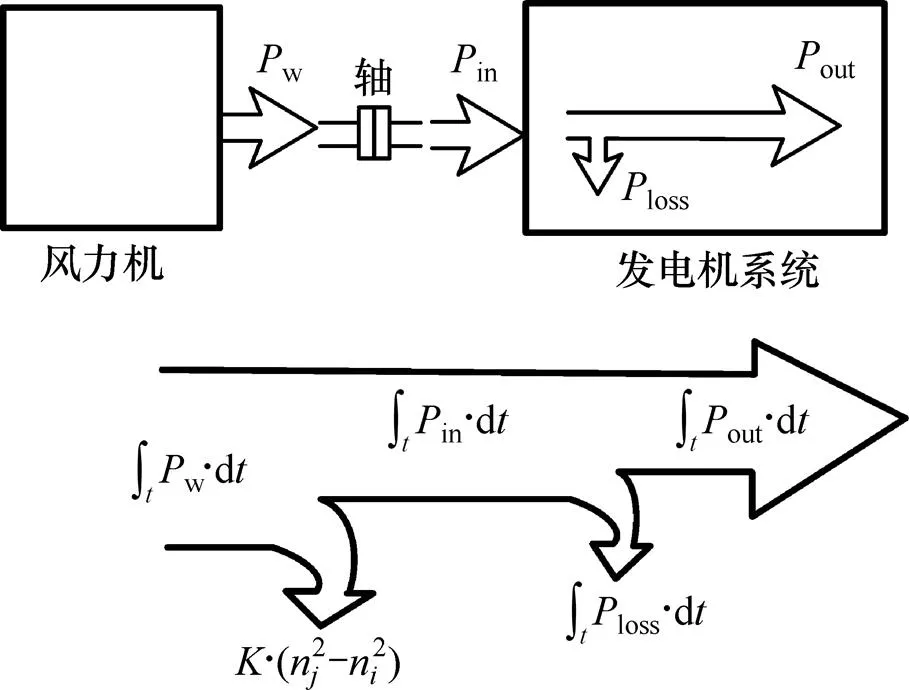
图2 离网型风力发电系统的能量流程图

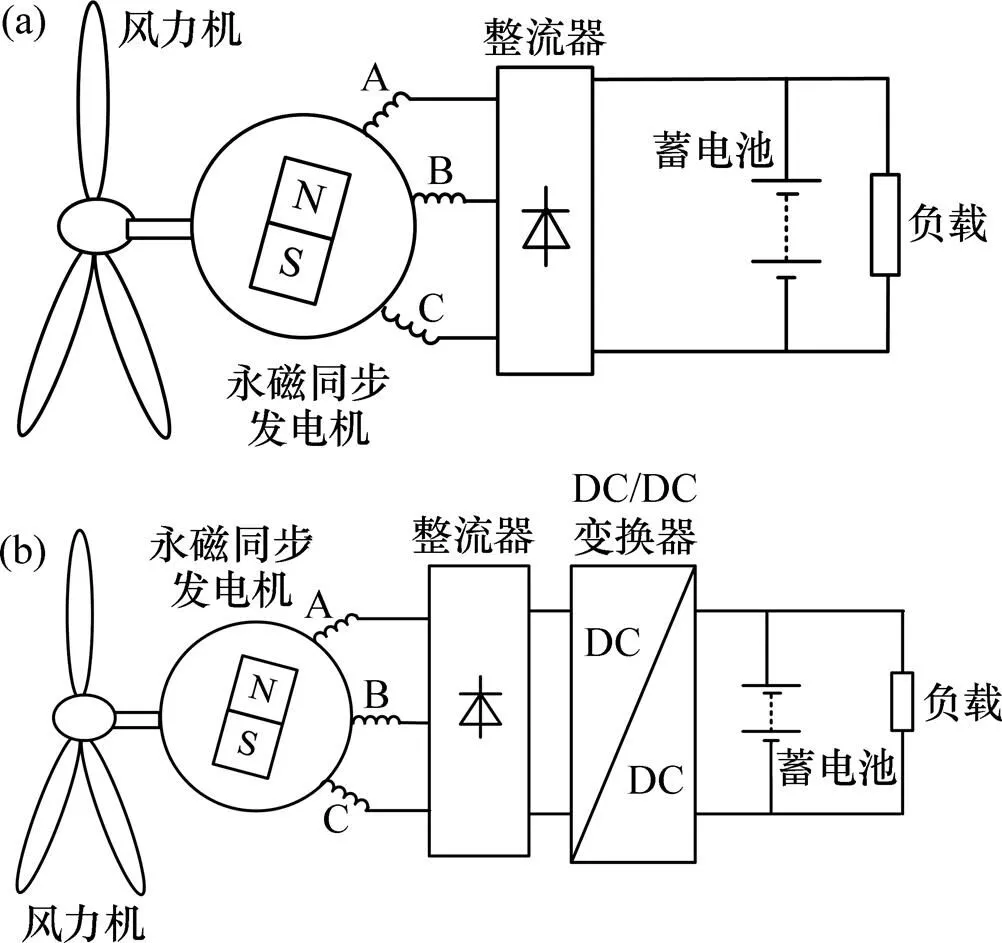
(a) 未采用任何MPPT方法的传统离网型风力发电系统；(b) 采用电控MPPT方法的传统离网型风力发电系统

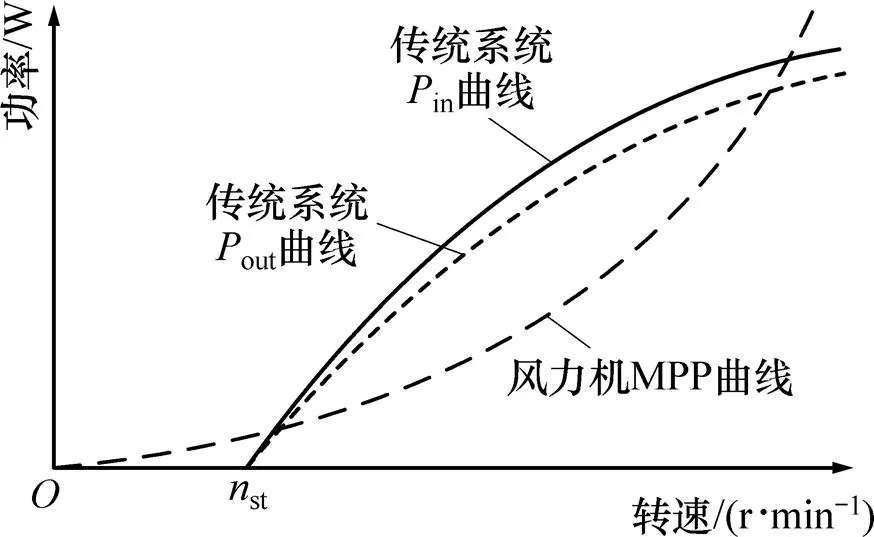
图4 未采用任何MPPT方法的传统发电机系统的特性

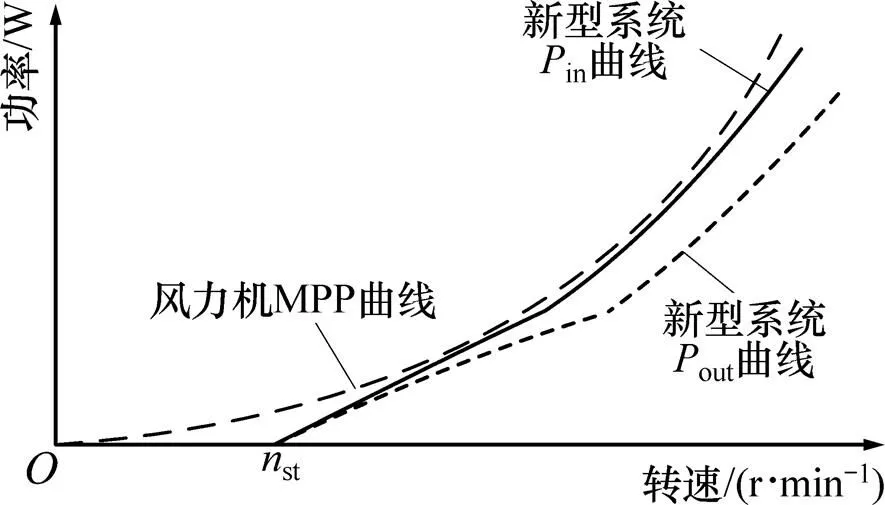
图5 为实现无源MPPT发电机系统所应该具有的特性

在初始时刻0，风速的初始值为0，如图6所示。相应地，风力机和发电机系统在时刻0的初始工作点均为点，如图7所示。在时刻1，风速阶跃变为s，而由于惯性，转速不会跃变。相应地，风力机的特性曲线瞬间由w(0)曲线变成了w(s)曲线，而由于转速未变，发电机系统的工作点还是点。由图7可知：此时w大于in，故整个系统的转速会逐渐上升，于是风力机的工作点沿着w(s)曲线上升，而发电机系统的工作点沿着in曲线上升。最终当转速升高到s时，w等于in，转速停止变化。由于发电机系统的in曲线非常接近风力机的MPP曲线，故此刻风力机稳定在了风速s下的最大功率点(即点)，从而完成了无源MPPT。

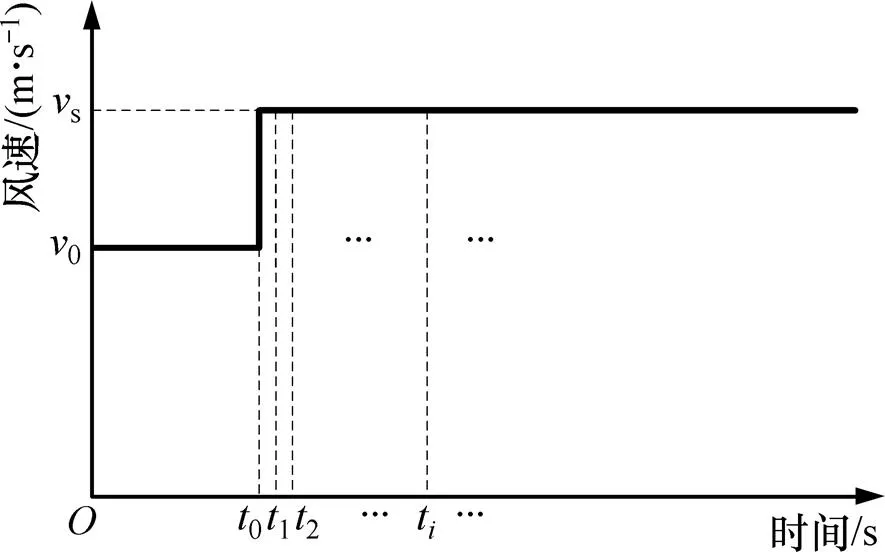
图6 风速与时间的关系

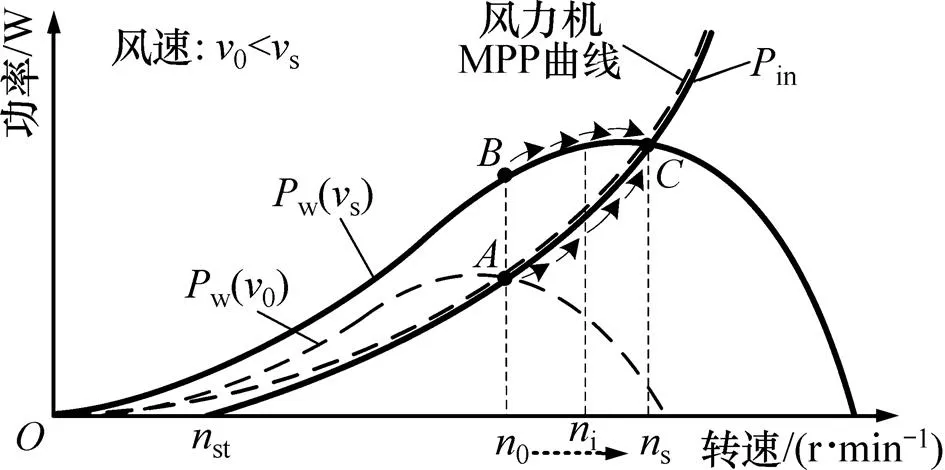
图7 无源MPPT的跟踪过程

2 采用无源MPPT方法的新型发电机系统

由图4与图5可知：传统发电机系统的特性并不满足无源MPPT方法的实现条件。为了满足该条件，需要采用：

1) 新的系统电路拓扑。

2) 新结构的发电机。

本文以规格为1kW的新系统为例进行论证。

2.1 新型发电机系统的电路拓扑

新型发电机系统由1台双绕组永磁同步发电机、2个不可控整流器、1台蓄电池及负载构成，如图8所示。图中：d1为绕组1整流输出电流的平均值；d2为绕组2整流输出电流的平均值；d为发电机系统直流母线电流的平均值。蓄电池的两端电压变化较小，可以稳定负载的输入端电压。发电机绕组1的每相匝数多于绕组2的每相匝数，所以，绕组1在较低转速时就能够克服蓄电池电压从而输出电流，而绕组2只有在较高转速时才能克服蓄电池电压输出电流，所以绕组1被称为低速绕组，绕组2被称为高速绕组。在较低转速时，风力机MPP曲线的数值较低，因此，绕组1必须具有较大的电感，以抑制系统的输出、输入功率，使系统的in曲线在较低转速时吻合风力机的MPP曲线。绕组2具有较小的电感，因此，绕组2在较高转速时可以输出较大的功率，以使发电机系统的P曲线在较高转速时吻合风力机的MPP曲线，如图9所示。图中：out1为绕组1的输出功率；out2为绕组2的输出功率；st为绕组1开始输出电能的起始转速，即新型发电机系统的建压转速；2为绕组2开始输出电能的起始转速。

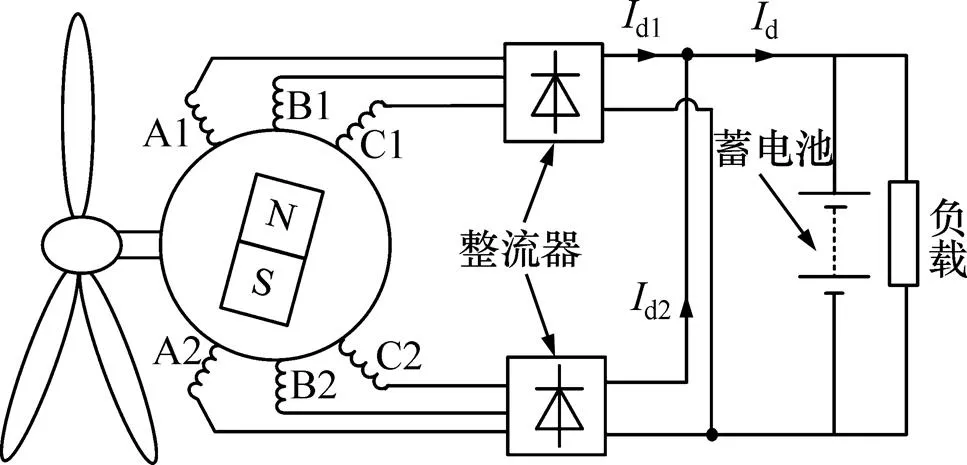
A1相，B1相，C1相—绕组1；

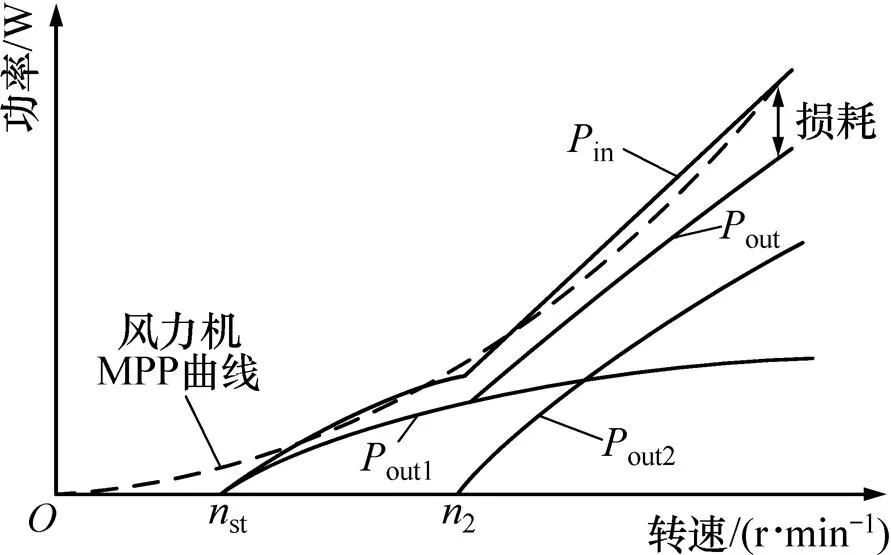
图9 新型发电机系统特性

2.2 新型发电机

为了实现无源MPPT，不仅需要采用新的系统电路拓扑，新型系统中所包含的发电机也必须具有新结构。如图10(a)所示，新结构发电机含有2套三相绕组，并且每槽中间置有电抗调整片。

电抗调整片将发电机的每个槽分成了上下2个小槽，绕组1的线圈边全部置于靠近机壳一侧的小槽内，而绕组2的线圈边全部置于靠近转子一侧的小槽内。在每个小槽内，每套绕组均为单层绕组。2套绕组分别Y型连接且中性点相互绝缘，绕组1中的每相匝数较多，绕组2中的每相匝数较少。

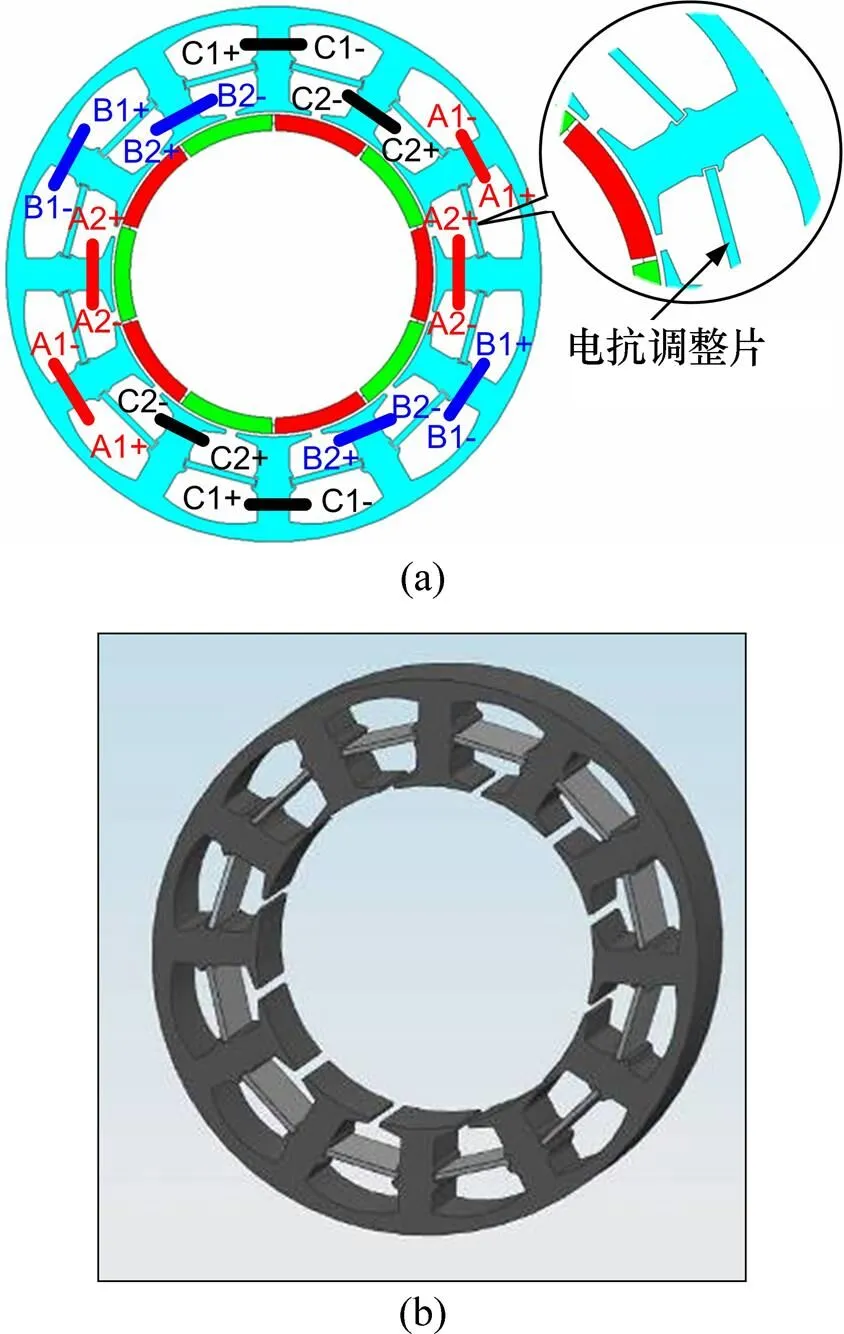
(a) 新型发电机的绕组结构；(b) 新型发电机的定子结构

绕组1含有较多匝数，所以在较低转速时只有绕组1能够克服蓄电池电压输出电能(绕组2此时截止)。绕组1中的电流产生的磁通一部分经由槽中间的电抗调整片闭合，另一部分由气隙主磁路闭合，如图11所示。相比于传统发电机，电抗调整片增大了绕组1的槽内漏磁导，因此，绕组1中每相电感值较大，可以有效抑制绕组1在低速时的输出、输入功率特性，如图12所示。

根据磁路理论，磁场分布遵循磁阻最小原理。由于电抗调整片与槽壁之间存在气隙(通常为0.3mm)，永磁体的磁通和绕组2电流的磁通都几乎不通过电抗调整片，而只有绕组1的电流磁通大量地通过电抗调整片(图11)。因此，电抗调整片只影响绕组1的电流磁路，而对永磁体磁路和绕组2电流磁路几乎没有影响。电抗调整片的厚度较薄，随着绕组1中的电流上升，电抗调整片将逐渐饱和。因为系统工作的频率很低(最大为33.3Hz)，且电抗调整片的体积占整个发电机的体积的比例很小，所以，电抗调整片的铁损值很小，经有限元计算，总量仅为1.3W，平均每个电抗调整片产生的铁损值仅为0.11W。因此，即使电抗片容易饱和，电抗调整片产生的铁损值也非常小，不会影响整个电机的效率，也不会产生过高的温升。

当发电机系统的转速进一步上升达到较高转速时，风力机的MPP曲线的数值和斜率大幅增大，此时需要绕组2开始输出电能，以使发电机的输入功率特性曲线能够继续吻合风力机的MPP曲线。

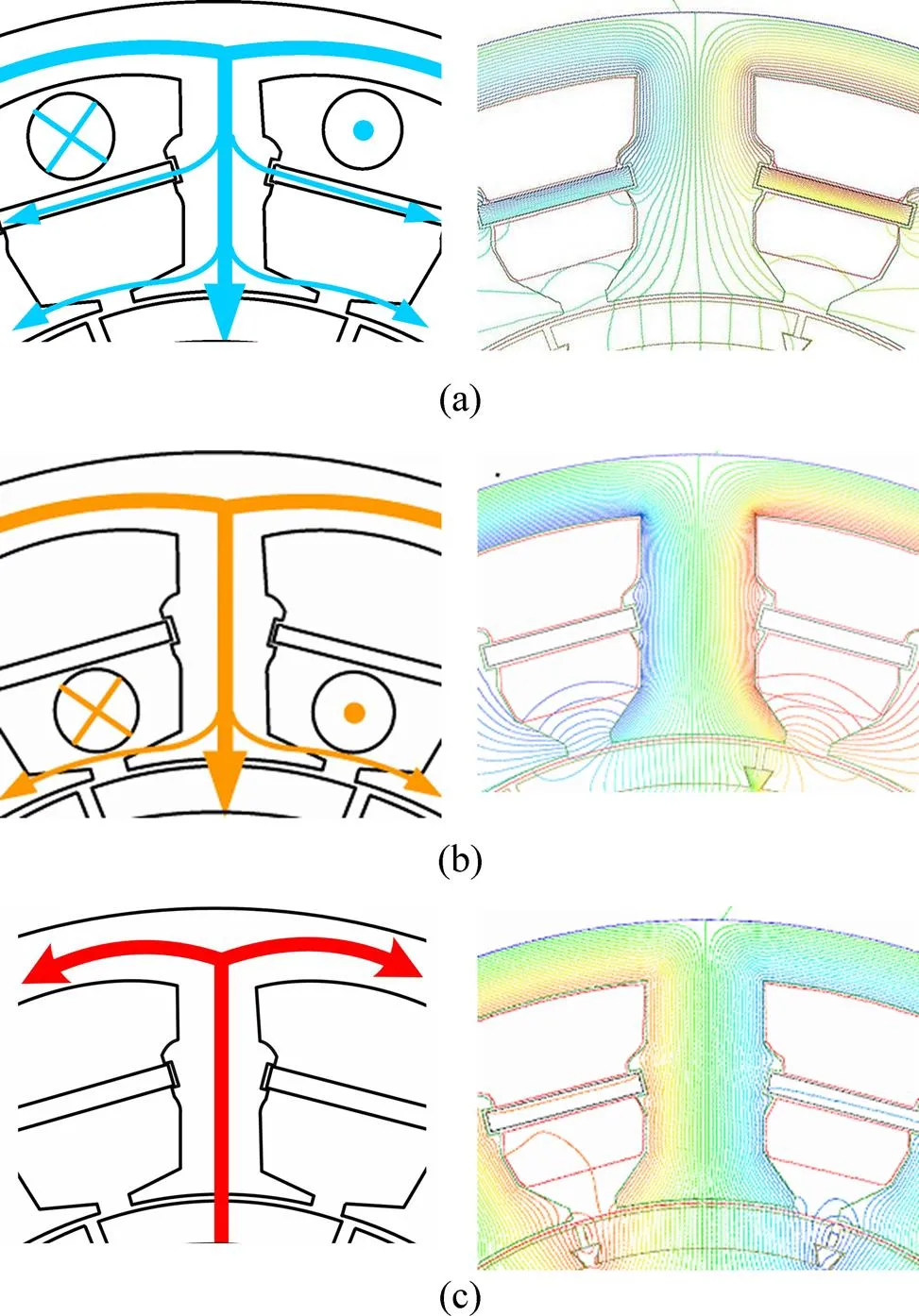
(a) 绕组1电流的磁通路径的示意图和有限元仿真结果；(b) 绕组2电流的磁通路径的示意图和有限元仿真结果；(c) 永磁体磁通路径的示意图和有限与仿真结果

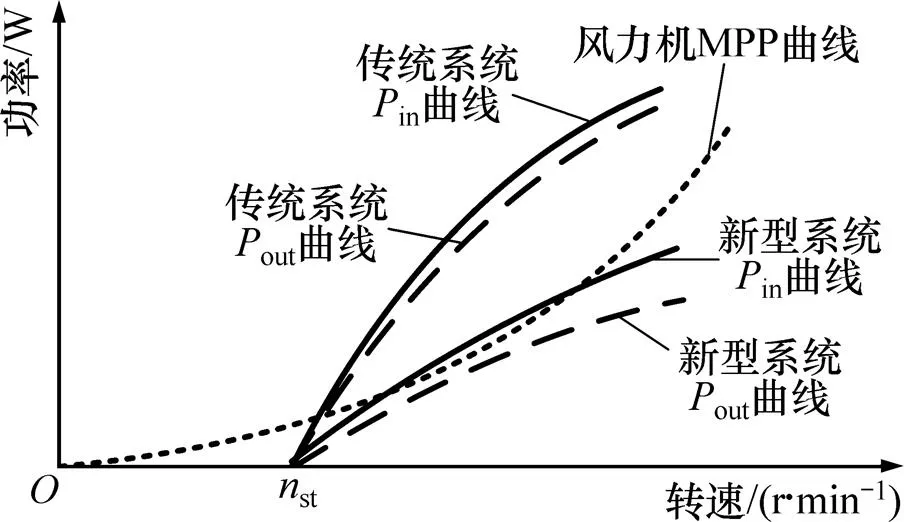
图12 低速时的特性比较

为获得较佳的曲线吻合效果，绕组2需要比绕组1在额定点处分担更多输出功率。因为绕组2的所有线圈均置于靠近转子一侧的小槽内，所以电抗调整片对绕组2的电流磁路并无直接影响，故绕组2的电感值较小，在高转速时可以输出较大电流。

2.3 新型发电机系统的数学模型

由电机理论可知，绕组1每相空载反电势为

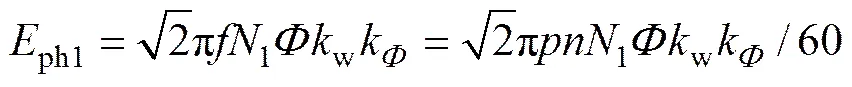
其中：ph1为绕组1每相空载反电势；为每极磁通量；1为绕组1每相匝数；为极对数；w为绕组系数；k为磁通波形系数。

式(6)表明：绕组反电势与转速、匝数成正比。由整流理论可知，绕组1空载状态下的整流电压为

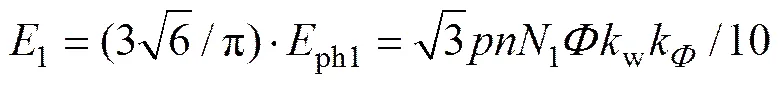
其中：1为绕组1空载整流输出电压的平均值。

当转速上升到超过建压转速时，即式(7)超过电池电压时，绕组1开始输出电流。同理，绕组2空载状态下的整流电压为

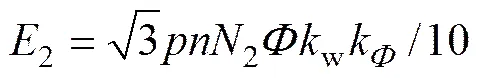
其中：2为绕组2空载整流输出电压的平均值。

式(7)和式(8)表明：由于绕组1的每相匝数(A1相、B1相和C1相)多于绕组2的每相匝数(A2相、B2相和C2相)，1与关系曲线的斜率大于2与关系曲线的斜率。因此，绕组1在低转速时就能克服蓄电池电压从而输出电能，而绕组2只有在较高转速时才能克服蓄电池电压输出电能。因此，建压转速可由下式计算得出：

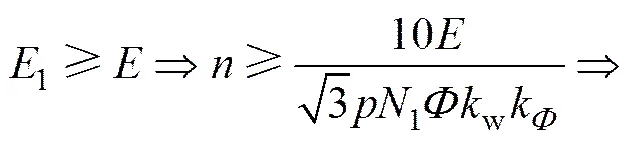
(9)

其中：st为绕组1开始输出电能的起始转速，即新型发电机系统的建压转速。

首先讨论单绕组工作模式，即只有绕组1输出电能时的情况。根据电机理论，图13所示为在单绕组工作模式下的发电机系统的等效电路。由图13可见：除了包含非线性电感，该电路与常规发电机系统的等效电路基本相同。因此，新型发电机系统直流侧电压方程类似于传统发电机系统，即：

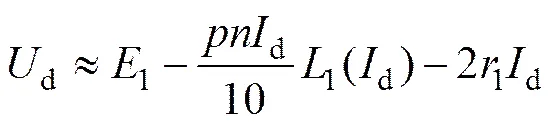
(11)

其中：d为直流母线电压的平均值；为蓄电池电压；d为发电机系统直流母线电流的平均值；1为绕组1每相自感，其数值是相电流的函数；1为绕组1每相电阻。

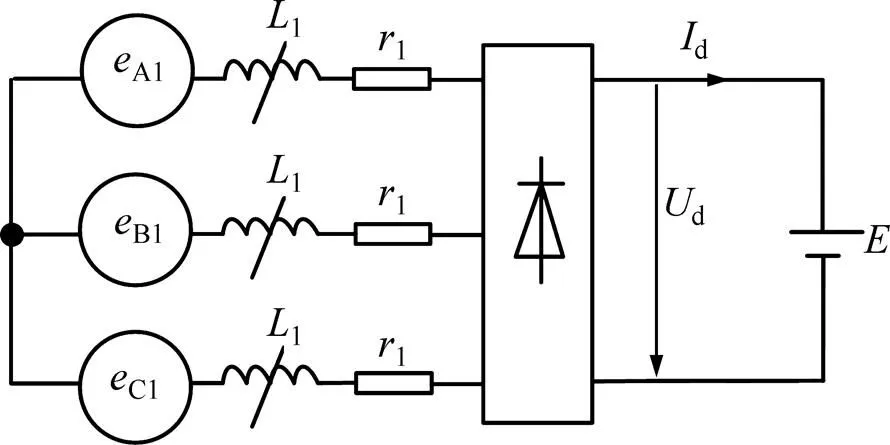
图13 单绕组工作模式下的系统等效电路

由式(10)与式(11)可知：单绕组工作模式下发电机系统的输出、输入功率为：

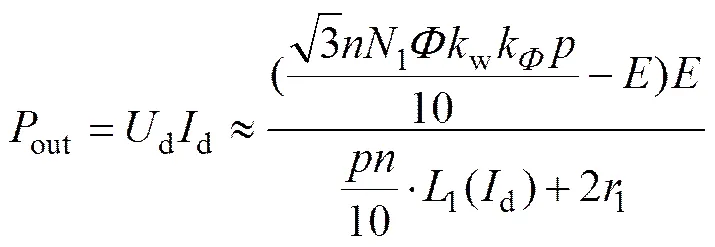
(13)

由于1为非线性参数，式(12)是一个隐式方程，不能直接求解。根据电机理论可知：电抗调整片为绕组1提供了较高的漏电感，所以1具有较大值。根据式(12)可知：较大的1可以抑制输出功率系统的输出功率和输入功率在低速时能拟合风力机的MPP曲线。

由图9可知：当转速持续上升时，风力机MPP曲线的斜率越来越大。因此，在较高转速时，仅仅依靠绕组1并不能持续地吻合风力机的MPP曲线，此时绕组2必须开始输出电能，以使发电机系统的输入功率曲线在高转速时继续吻合风力机的MPP曲线。双绕组工作模式时(即绕组1与绕组2同时输出电能时的情况)系统的等效电路示意图如图14所示。图中：是绕组1和绕组2之间的互感。绕组1电流在绕组2中产生的电压降为3MI1。因此，双绕组工作模式下绕组2开始输出功率的起始转速可以按下式计算：

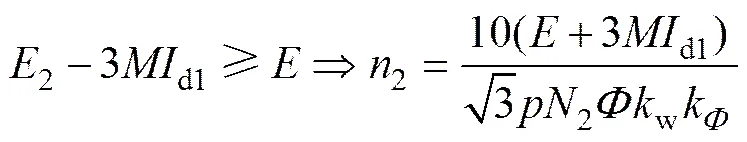
其中：2为绕组2的每相匝数；为绕组1与绕组2之间的互感；2为绕组2开始输出电能的起始转速。

高速模式下发电机系统直流侧的电压和功率方程为：

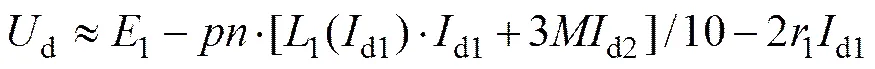
(16)

图14 双绕组工作模式下的系统等效电路

Fig. 14 Equivalent circuit of new system in double- winding-operating mode

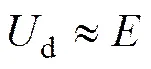
(18)

(19)

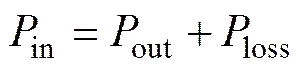
其中：d1为绕组1整流输出电流的平均值；d2为绕组2整流输出电流的平均值；2为绕组2每相自感；2为绕组2每相电阻。

上述方程也是隐式方程，需要借助数值方法进行求解。用有限元法可以计算得到新型发电机的电感，结果如图15所示。由图15可见：2较小，因此绕组2可以输出较大的电流。图16所示为实测值与数学模型计算值之间的对比。由图16可知数学模型是正 确的。

2.4 与传统发电机的结构对比

双绕组结构看似比单绕组结构更复杂，事实上，双绕组结构仅仅是在内部接线方式上与单绕组结构不同。图17所示为传统发电机与新型发电机的绕组结构对比。可见新型发电机的绕组结构并不比传统发电机的绕组结构更复杂。

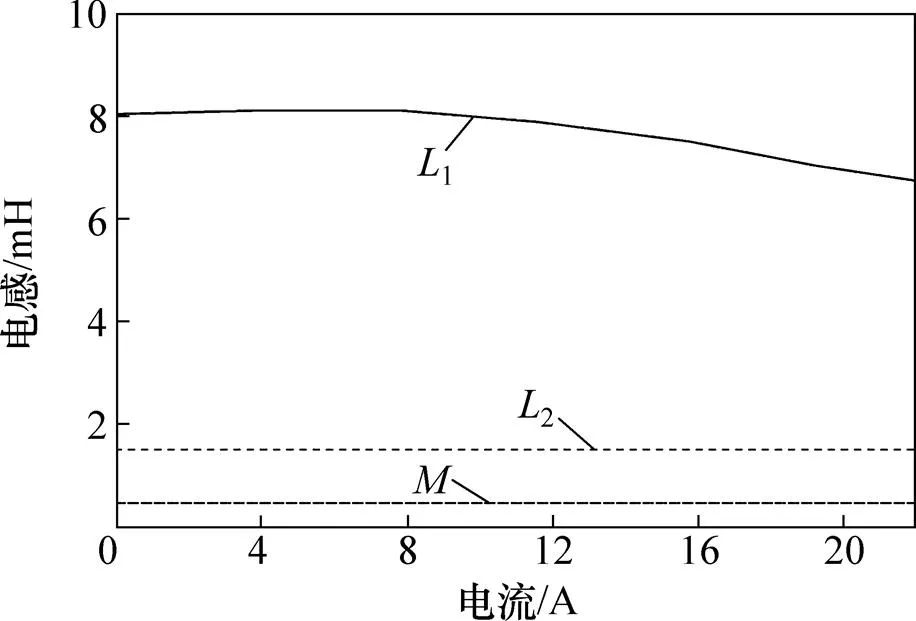
图15 电感与电流的关系

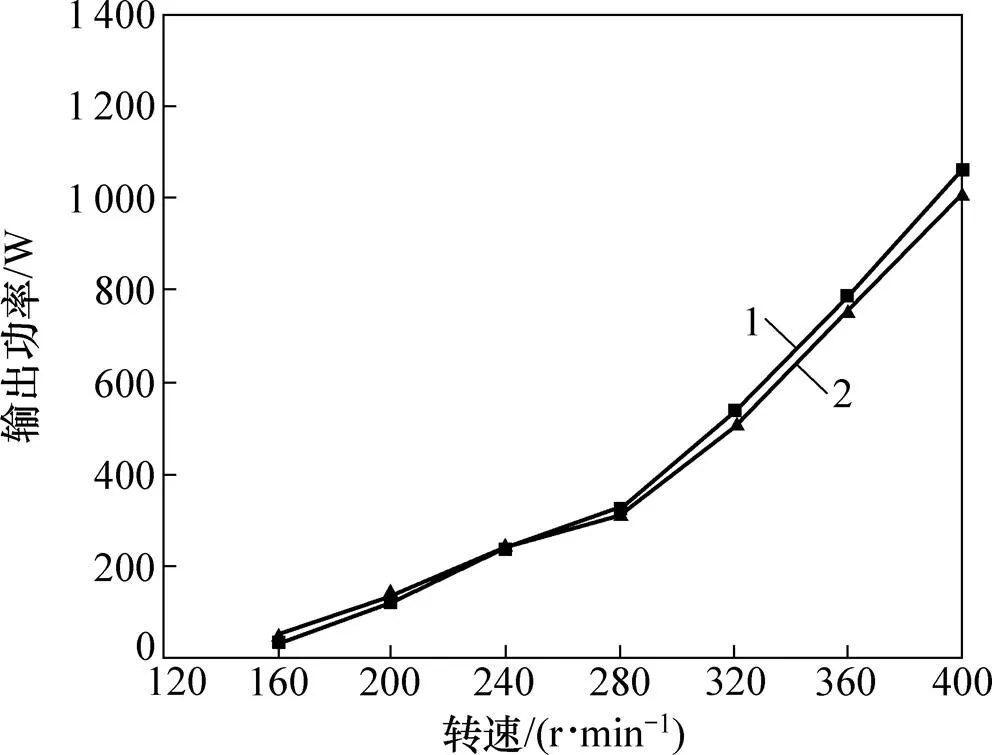
1—计算值；2—实测值。

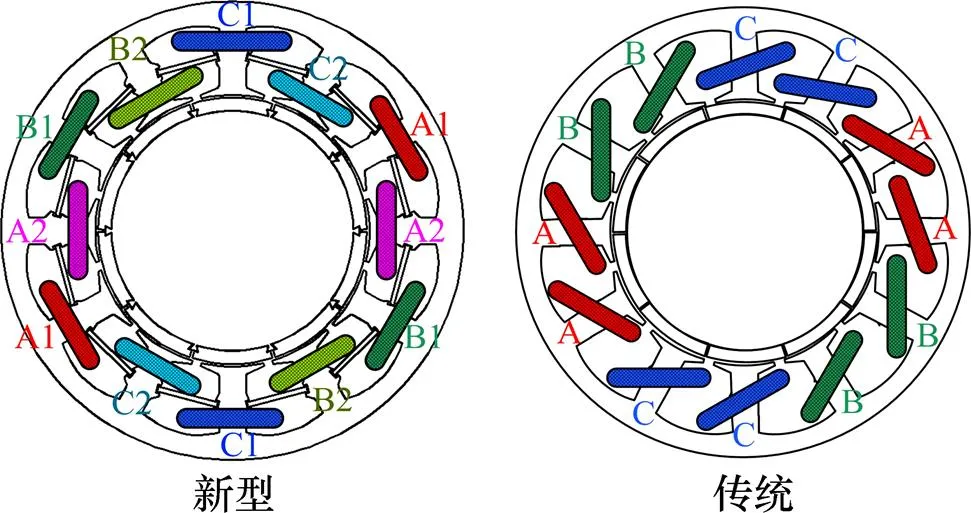
图17 新型发电机与传统发电机的绕组结构对比

虽然双绕组并没有增大新型发电机绕组结构的复杂性，但电抗调整片还是使得新型发电机的定子结构稍微复杂，这增加了定子的工艺成本。然而，新型发电机系统比传统系统省略了成本较高的DC/DC变换器(仅仅增加了1个二极管整流器，其价格仅为15元人民币左右)，所以相比于传统风力发电机系统，新型风力发电机系统在总体成本上并无劣势。

3 样机及实验

课题组设计并制造了规格为1kW的样机并按照图8组成了新型系统，具体尺寸及主要参数如表1所示。

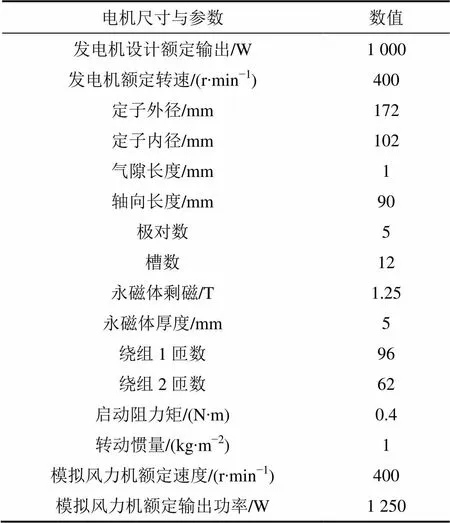
表1 样机系统参数

图18所示为新型发电机的定子冲片照片。电机的齿壁中央有槽口，以方便安装电抗调整片。通过拖动实验，可得发电机系统的输入、输出特性如图19所示。由图19可知：电机在转速低于160 r/min时即可输出电能；发电机系统的输入功率特性曲线能够在较宽转速范围内很好地吻合风力机的MPP曲线。

图20所示为新型发电机系统的效率特性。由图20可知：当转速高于200 r/min时，整个系统的效率一直保持在较高水平(基本大于0.8)。在转速为280 r/min时，新型系统的效率有1个相对低点，这是因为：绕组1的高效率转速区间为低转速段；绕组2的高效率转速区间为高转速段；双绕组结构将2套绕组的高效率区间叠加在一起，从而扩大了系统的高效率转速区间范围。该图揭示了新方法的另一个优点：具有宽广的高效率转速范围。

图20显示整个系统具有较高的效率(市场上传统小型风力发电机系统的效率为75%~80%)。

图18 新型发电机的定子照片

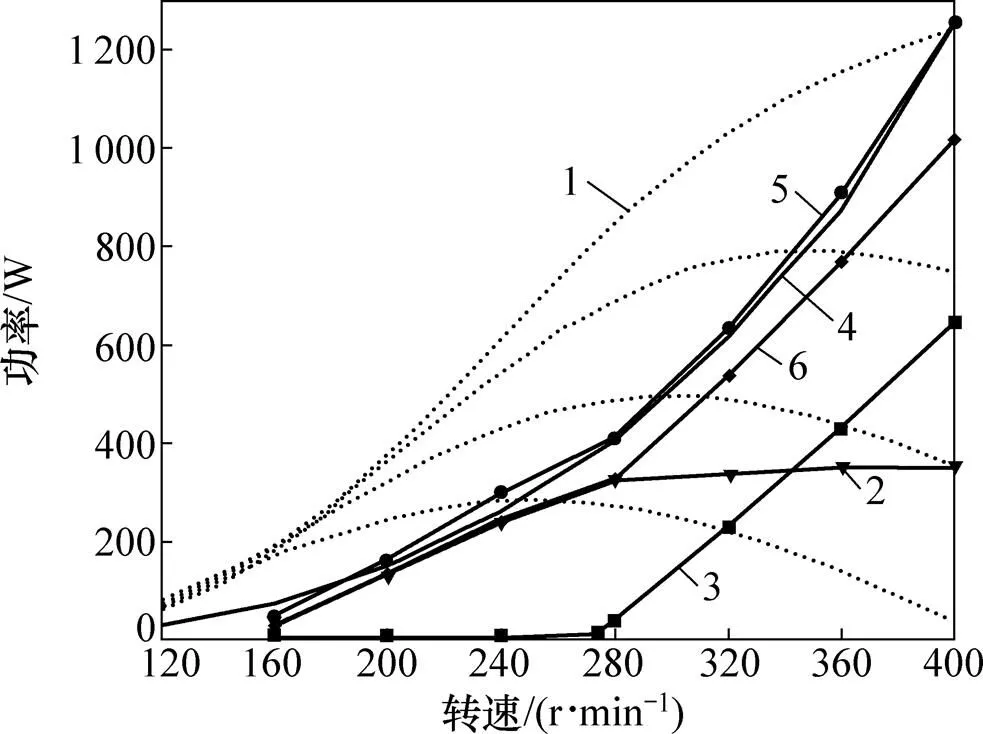
1—不同风速下风力机的输出功率；2—Pout1；3—Pout2；3—风力机MPP曲线；4—Pin；5—Pout。

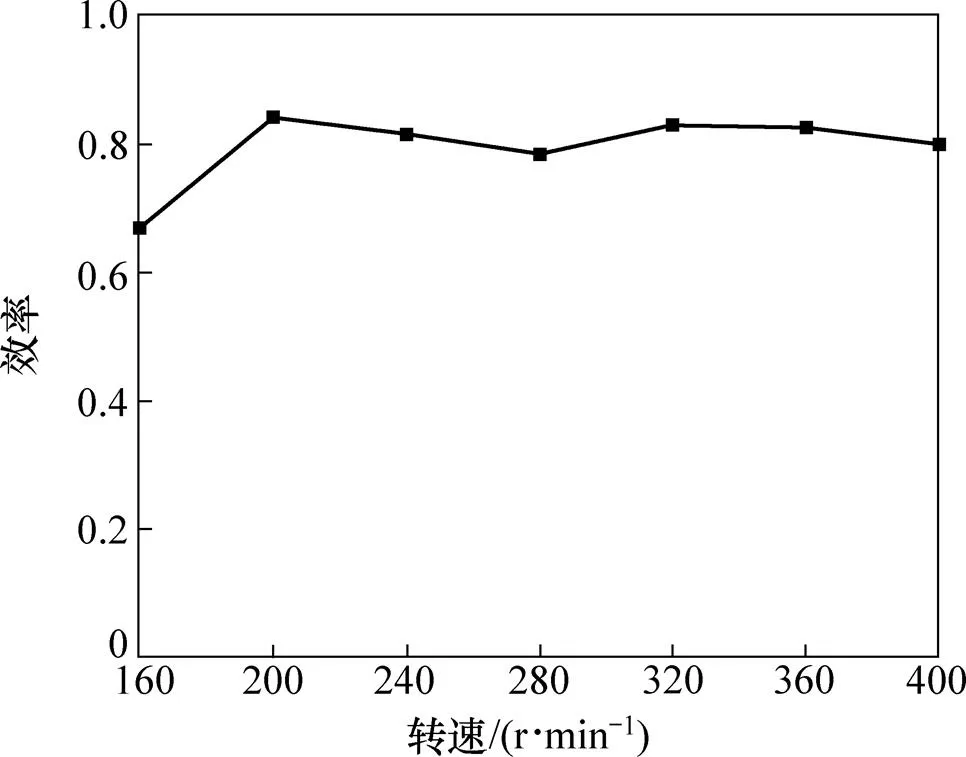
图20 样机系统的效率特性

图21所示为MPPT实验平台的结构框图。图中：ref为单片机输出的参考转矩信号；w为变频器输出的实际转矩信号。该实验使用变频器、电动机、单片机以及转动惯量盘来模拟风力机。单片机根据风速信号、转速信号以及风力机参数计算得到参考转矩信号，并将该转矩信号传达给变频器，最终由变频器控制电动机输出实际转矩；惯量盘由1个铁盘加多个负重铁块组成，能够模拟风力机的转动惯量。综上可知，该实验平台能够较好地模拟风力机特性。

图22所示为实验结果。需要指出：依据风力机理论，风力机运行在最大功率点时，其功率系数最大，约为0.48。因此，评判系统是否成功完成MPPT的标准为：风力机的功率系数是否接近0.48。

图22(a)所示为给定的风速信号曲线。本实验采用实时风速轮廓线，文献[26]介绍了获得实时风速信号的方法。由图22(a)可见：风速最小值约为4.2 m/s，最大值约为7.8 m/s，这比额定值(8 m/s)稍低。图22(b) 所示为转速响应曲线。从图22(b)可见：发电机系统的转速变化趋势与风速的变化趋势一致。图22(c)所示为风力机的功率系数曲线。从图22(c)可见：在整个实验过程中，风力机的功率系数接近0.48，其平均值明显高于使用爬山法的传统系统，这证明新型发电机系统实现了MPPT。图22(d)所示为发电机的输出功率。从图22(d)可见：在时刻为97s时，新型系统的输出功率约为950 W，此时的风速为7.7 m/s，这些数据与额定值一致，表明被测系统运行正常，新型系统的输出功率大于传统系统。将输出功率随时间进行积分，可以得到发电机系统的输出能量，如图22(e)所示。从图22(e)可以看出：在140 s的时间内，新型系统的输出能量比传统系统多9kJ，提高约14.5%。

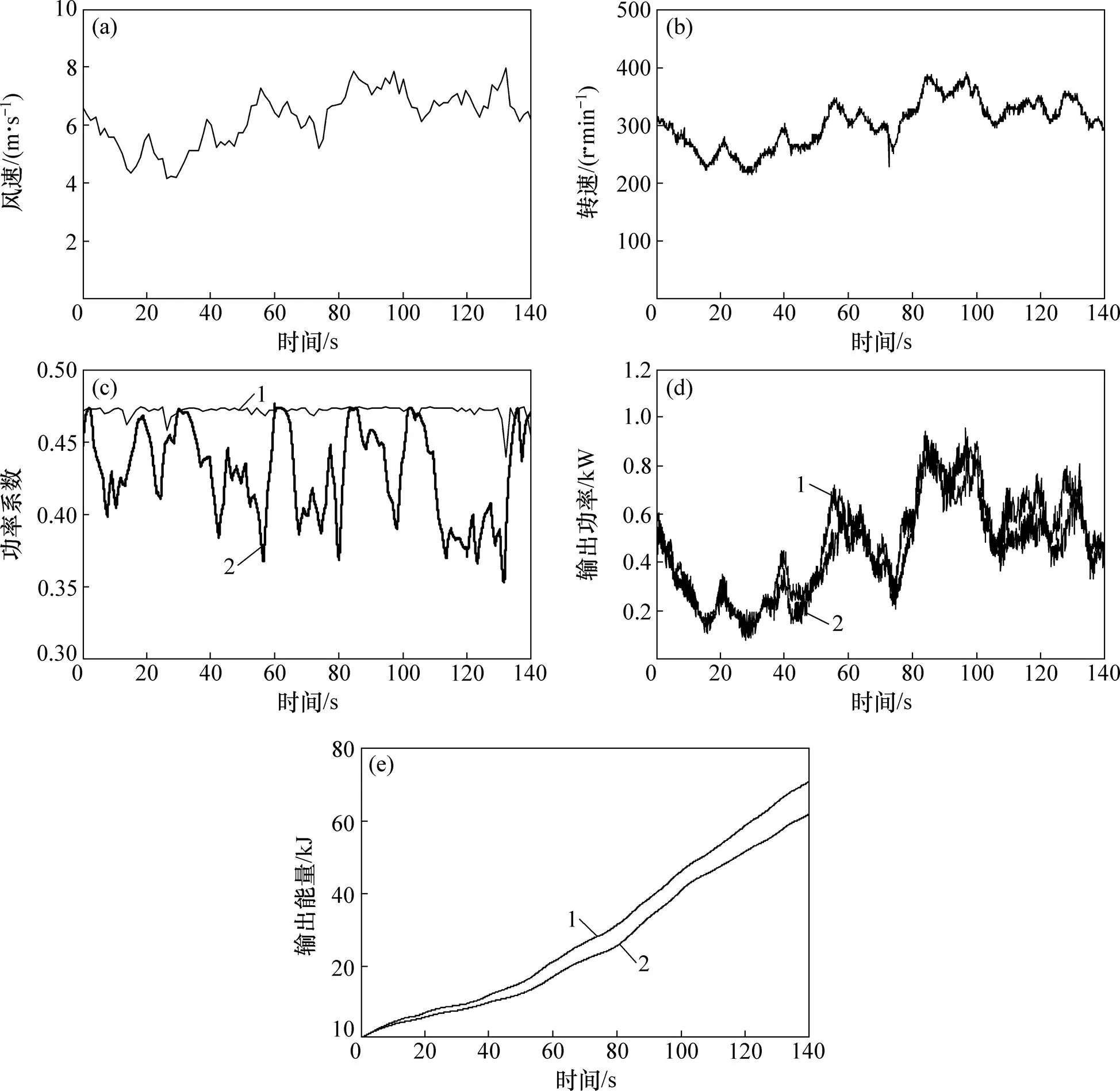
(a) 所施加的风速信号；(b) 新型系统的转速响应；(c) 风力机功率系数；(d) 系统的最终输出功率；(e) 系统的最终输出能量

使用无源MPPT方法的新型系统的动态MPPT性能明显优于使用HCS方法的传统系统的动态MPPT性能，根本原因在于HCS方法是盲目的，它并不“知道”趋向最大功率点的正确方向，这导致HCS方法存在响应较慢这个痼疾。相反，由于新型系统的输入特性曲线与风力机的MPP曲线相吻合，当风速变化时系统可以自动地趋向新的最大功率点，无需判断方向。因此，无源MPPT方法可以让新型系统更迅速地跟踪MPP，因而能够输出更多的电能。

综上所述，实验结果证明新型系统实现了无源MPPT，并且具有比传统系统更强的MPPT能力。

4 结论

1) 由于省略了大量电子控制元件，采用无源MPPT方法的新型系统比采用电控方法的传统系统有着更高的可靠性，从而能够更好地适应野外环境。

2) 无源MPPT方法的现实条件是：发电机系统的输入功率特性曲线与风力机的MPP曲线相吻合。为满足该实现条件需要对发电系统的电路拓扑以及发电机本体进行改进：系统电路拓扑采用双三相整流并联结构；新型发电机含有两套三相绕组并在每个槽内置有电抗调整片。

3) 在MPPT实验中，当风速变化时，风力机功率系数始终接近0.48，证明新型系统实现了无源MPPT；在140 s的时间内，新型系统的输出能量比传统系统多9 kJ，提高约14.5%，证明新型系统的动态性能优于使用HCS方法的传统系统的动态性能。

[1] 程明, 张运乾, 张建忠. 风力发电机发展现状及研究进展[J]. 电力科学与技术学报, 2009, 24(3): 2−9.CHENG Ming, ZHANG Yunqian, ZHANG Jianzhong. Development and research progress of wind power generators[J]. Journal of Electric Power Science and Technology, 2009, 24(3): 2−9.

[2] HUI Li, ZHE Chen. Overview of different wind generator systems and their comparisons[J]. IET Renewable Power Generation, 2008, 2(2): 123−138.

[3] 陈家伟, 陈杰, 龚春英. 离网风力发电系统功率控制与能量管理策略[J]. 中国电机工程学报, 2012, 32(S1): 7−14. CHEN Jiawei, CHEN Jie, GONG Chunying. Power control and energy management strategy for a stand-alone WECS[J]. Proceedings of the CSEE, 2012, 32(S1): 7−14.

[4] 年街, 曾嵘. 分布式发电系统离网运行模式下输出电能质量控制技术[J]. 中国电机工程学报, 2011, 31(12): 22−28.NIAN Heng, ZENG Rong. Control technique on output power quality for distributed generation system under stand-alone operation mode[J]. Proceedings of the CSEE, 2011, 31(12): 22−28.

[5] BAROTE L, MARINESCU C, CIRSTEA M N. Control structure for single-phase stand-alone wind-based energy sources[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 764−772.

[6] WAI Rongjong, LIN Chungyou, DUAN Chunyu, et al. High efficiency power conversion system for kilowatt-level stand-alone generation unit with low input voltage[J]. IEEE Transactions on Industrial Electronics, 2008, 55(10): 3702−3714.

[7] VASQUEZ J C, GUERRERO J M, LUNA M, et al. Adaptive droop control applied to voltage-source inverters operating in grid-connected and islanded modes[J]. IEEE Transactions on Industrial Electronics,2009, 56(10): 4088−4096.

[8] PENA R, CARDENAS R, PROBOSTE J, et al. Sensorless control of doubly-fed induction generators using a rotor-current-based MRAS observer[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 330−339.

[9] ZHOU Tao, FRANCOIS B. Energy management and power control of a hybrid active wind generator for distributed power generation and grid integration[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 95−104.

[10] BARAKATI S M, KAZERANI M, APLEVICH J D. Maximum tracking control for a wind turbine system including a matrix converter[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 705−713.

[11] TAN K, ISLAM S. Optimum control strategies in energy conversion of PMSG wind turbine system without mechanical sensors[J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 392−399.

[12] CHEN Z, SPOONER E. Grid power quality with variable speed wind turbines[J]. IEEE Transactions on Energy Conversion, 2001, 16(2): 148−154.

[13] PAN C, JUAN Y. A novel sensorless MPPT controller for a high-efficiency microscale wind power generation system[J]. IEEE on Energy Conversion, 2010, 25(1): 207−216.

[14] CHEN Jie, CHEN Jiawei, GONG Chunying. Constant- bandwidth maximum power point tracking strategy for variable-speed wind turbines and its design details[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 5050−5058.

[15] MORIMOTO S, NAKAYAMA H, SANADA M, et al. Sensorless output maximization control for variable-speed wind generation system using IPMSG[J]. IEEE Transactions on Industrial Application, 2005, 41(1): 60−67.

[16] ZHU Ying, CHENG Ming, HUA Wei, et al. A novel maximum power point tracking control for permanent magnet direct drive wind energy conversion systems[J]. Energies, 2012, 5(5): 1398−1412.

[17] DATTA R, RANGANATHAN V T. A method of tracking the peak power points for a variable speed wind energy conversion system[J]. IEEE Transactions on Energy Conversion, 2003, 18(1): 163−168.

[18] KOUTROULIS E, KALAITZAKIS K. Design of a maximum power tracking system for wind-energy-conversion applications[J]. IEEE Transactions on Industrial Electronics, 2006, 53(2): 486−494.

[19] WANG Q, CHANG Liuchen. An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1242−1249.

[20] AGARWAL V, AGGARWAL R K, PATIDAR P, et al. A novel scheme for rapid tracking of maximum power point in wind energy generation systems[J]. IEEE Transactions on Energy Conversion, 2010, 25(1): 228−236.

[21] DALALA Z M, ZAHID Z U, YU Wensong, et al. Design and analysis of an mppt technique for small-scale wind energy conversion systems[J]. IEEE Transactions on Energy Conversion, 2013, 28(3): 756−767.

[22] SIMOES M G, BOSE B K, SPIEGEL R J. Fuzzy logic based intelligent control of a variable speed cage machine wind generation system[J]. IEEE Transactions on Power Electronics, 1997, 12(1): 87−95.

[23] GALDI V, PICCOLO A, SIANO P. Designing an adaptive fuzzy controller for maximum wind energy extraction[J]. IEEE Transactions on Energy Conversion, 2008, 23(2): 559−569.

[24] LI Hui, SHI K L, MCLAREN P G. Neural-network-based sensorless maximum wind energy capture with compensated power coefficient[J]. IEEE Transactions on Industrial Application, 2005, 41(6): 1548−1556.

[25] 张秀玲, 谭光忠, 张少宇, 等. 采用模糊推理最优梯度法的风力发电系统最大功率点跟踪研究[J]. 中国电机工程学报, 2011, 31(2): 119−123.ZHANG Xiuling, TAN Guangzhong, ZHANG Shaoyu, et al. Research on maximum power point tracking of wind power generation system based on fuzzy inference optimal gradient[J]. Proceedings of the CSEE, 2011, 31(2): 119−123.

[26] NICHITA C, LUCA D, DAKYO B, et al. Large band simulation of the wind speed for real time wind turbine simulators[J]. IEEE Transactions on Energy Conversion, 2002, 17(4): 523−529.

(编辑 陈爱华)

Passive MPPT method for stand-alone wind power generation systems

BAI Yinru, KOU Baoquan, CHAN C C

(School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China)

Conventional maximum power point tracking (MPPT) methods used for stand-alone wind power generation systems (SWPGS) have low reliability, and thus a passive solution for MPPT was presented. Using a special structural design, it is possible to create a new generator system where the input power vs. rotor speed curve naturally fits to the wind turbine maximum power point (MPP) curve. This characteristic allows the proposed system to automatically realize MPPT without the use of any algorithm or electrical control device, thereby resulting in high reliability. The principle of the passive MPPT method was analyzed, and the mathematical model of the proposed system was established. The results show that the proposed system adopting the passive MPPT method can realize the passive MPPT, and its dynamic performance of MPPT is better than that of the conventional system using hill-climbing searching method.

maximum power point tracking (MPPT); passive; permanent magnet synchronous generator; stand-alone; wind power generation

10.11817/j.issn.1672−7207.2017.02.015

TM351

A

1672−7207(2017)02−0370−11

2016−03−22；

2016−06−19

国家高技术研究发展计划(863计划)项目(2009AA05Z446)(Project(2009AA05Z446) supported by the National High Technology Research and Development Program (863 Program) of China)

寇宝泉，博士，教授，从事特种电机研究；E-mail：koubq@hit.edu.cn